向量将几何代数化举例

林开亮 刘新亮

(西北农林科技大学 712100；天津市耀华中学 300040)

1 引言

多年前, 陈省身先生在接受人民教育出版社访谈[1], 曾对高中数学课程改革发表了他的看法, 作为几何学家, 他特别肯定了向量的重要性.

访: 现在高中数学课程改革, 教学内容要增加一些向量、算法、微积分、概率统计的内容, 您觉得这些内容在中学里是不是必须有的? 能不能教?

陈: 我想在高中里放进去都可以, 但都是要讲一些最基本的概念, 比如向量. 向量当然要紧, 向量使许多理论的数学代数化, 有向量这个东西在数学里头, 你可以算出数目来.比如, 它可以把几何代数化. 代数使得你能算, 可以解决很多问题. 我想对于你说的这些, 都可以讲一些最基本的东西.

陈先生最后一句话说“对于你所说的这些, 都可以讲一些最基本的东西”. 特别地，对于陈先生所钟爱的向量，更是如此.那么关于向量，我们究竟可以讲哪些最基本的东西呢？作者这里将结合自身教学研究的经验，以具体的例子来诠释陈先生这里所说的“向量可以将几何代数化”.

2 三个例子

例1勾股定理与余弦定理

陈先生曾指出[2]，欧几里得的《几何原本》中的几何结果主要有两个：一个是直角三角形的勾股定理，一个是三角形的内角和定理.勾股定理在国外称为毕达哥拉斯定理，但中国古代数学家也独立发现并给出了证明，例如利用著名的弦图.弦图曾经作为 2002年在北京召开的国际数学家大会的会标.

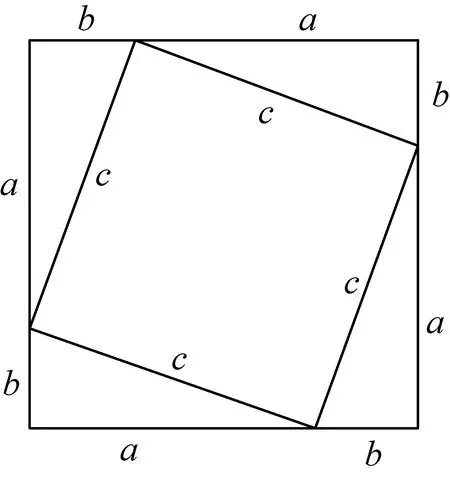
勾股定理的弦图证明：易知，图中的四个三角形是全等的，中间的四边形是一个正方形(四个角都是相等的，因此都为直角).大正方形的面积等于四个三角形的面积加上中间的小正方形的面积，写成数学表达式的形式就是

立即得到

a2+b2=c2.

毫无疑问，上述利用弦图的几何证明是非常巧妙的，并最终归结为一个简单的代数恒等式.但若我们采用向量的语言，勾股定理的叙述与证明都会更简洁.

我们用a·b表示两个平面向量(或空间向量)a,b的数量积(或称内积)，并将向量a的长度平方a·a简记为a2.现在我们可以给出勾股定理的向量表述与证明了.

定理1(勾股定理) 设a,b是互相垂直的平面向量(或空间向量)，则有

(a-b)2=a2+b2

(1)

证明根据数量积的运算法则，我们来计算左边：

(a-b)2=(a-b)·(a-b)

=a·a-a·b-b·a+b·b

=a2+b2-2a·b(a·b=b·a)

=a2+b2(a·b=0).

注意到，事实上，我们在证明过程中得到了更一般的余弦定理.

定理2(余弦定理)设a,b是平面向量(或空间向量)，则有

(a-b)2=a2+b2-2a·b

(2)

注意，正如李尚志老师在文[3]中指出的，对于一维向量(即实数)而言，等式(2)是我们初中阶段就已经熟悉的完全平方公式

(a-b)2=a2+b2-2ab

(3)

由余弦定理，不仅可以得到勾股定理，还可以得到其逆定理.这两个结果合在一起，恰好给出了直角三角形的特征刻画：

定理3设a,b是平面向量(或空间向量)，则a,b垂直当且仅当(a-b)2=a2+b2.

勾股定理和余弦定理也可以推广到多个向量的情形.例如，我们给出余弦定理的下述推广，读者不难自行证明(并从中得到勾股定理的一个显然推广).

定理4设a1,…,am是n维向量，则有

(4)

注意，当n=1且m=2时，(4)就成为我们熟悉的另一个完全平方公式

(a+b)2=a2+b2+2ab.

例2平行四边形等式

这是2010年菲尔兹奖获得者、法国数学家维拉尼(Cédric Villani)曾在接受记者采访(见文[6])时曾提及的一个例子.当访谈者问他在中学的数学学习经历中有什么特别之处，维拉尼说：“……我还记得对另一个定理的惊奇，这个定理说，在一个平行四边形中，两条对角线的平方和等于四条边的平方和，我被这个恒等式的简单和优美迷住了.”维拉尼所说的定理即平行四边形等式，它归功于古希腊几何学家阿波罗尼斯(Apollonius，约公元前262年—190年)，也称为阿波罗尼斯定理.用向量的语言，该定理可以表述如下：

定理5(平行四边形等式)设a,b是平面向量(或空间向量)，则有

(a+b)2+(a-b)2=2a2+2b2

(5)

不难发现，证明是平凡的(两次利用余弦定理).我们提请读者注意，该定理在一维向量的情况，称为我们熟悉的代数等式：(a+b)2+(a-b)2=2(a2+b2).

例3菱形与矩形的刻画

关于平行四边形，我们有两个基本的结果，它们分别刻画了菱形和矩形.平行四边形为菱形当且仅当对角线互相垂直；平行四边形为矩形当且仅当对角线等长.这两个结果也都可以用向量的语言方便地描述和证明.例如，前一个结果可用向量的语言翻译如下(其中⊥表示向量的垂直，从代数的角度讲，就是两个向量的数量积等于0)：

定理6设a,b是平面向量(或空间向量)，则有(a+b)⊥(a-b)当且仅当a2=b2.

证明的基础是下述向量等式：

(a+b)·(a-b)=a2-b2

(6)

这个等式在一维情形，就是我们所熟悉的平方差公式(a+b)(a-b)=a2-b2.

注定理6在高等几何学中有一个有趣的应用，即用来证明欧几里得空间的保持垂直关系不变的线性变换是正交变换的常数倍[5].

类似地，我们可以用向量来翻译下述结果：平行四边形为矩形当且仅当对角线等长.

定理7设a,b是平面向量(或空间向量)，则有a⊥b当且仅当(a+b)2=(a-b)2.

类似地，该证明依赖于一个向量等式：

4a·b=(a+b)2-(a-b)2

(7)

在一维情形，所对应的等式也是为我们所熟知的：

4ab=(a+b)2-(a-b)2.

3 可延伸为练习的例子

李尚志老师在文[3][4]中举出了更多的例子介绍中学数学中的向量方法，我们这里再补充三个，它们与本文的上述例子精神更契合，可以考虑作为习题留给对此方法有兴趣的学生.

2.若向量a1,a2,a3两两垂直, 则对于任意的向量b有

‖a1+a2+a3-b‖2+2‖b‖2=‖a1-b‖2

+‖a2-b‖2+‖a3-b‖2

(8)

3.设S是半径为1的球面，P是单位球内一点(‖OP‖<1)，从点P出发引三条两两垂直的射线交球面S于A,B,C三点，以PA,PB,PC为棱构造长方体，设点Q为所作长方体与P相对的顶点，求点Q的轨迹.

注本题是1978年第20届国际数学奥林匹克竞赛的第二题, 同时也是 2007年北京大学数学科学学院的研究生招生考试“高等代数与解析几何”试卷第7题. 一个简单的向量解法可以用练习2的结果，参见[8].

4 小结：作为联系几何与代数之纽带的向量

正如上述几个简单的例子所揭示的，向量确实是描述几何的一门恰当语言，一方面，借助于它，可以探索高维空间的几何，达到几何直观难以起作用的领域；另一方面，在一维的情况，向量退化成普通的数，从而向量的理论又成了数的理论的一个自然推广.简而言之，向量确实是一个基本而自然的概念，这也许就是陈省身先生为什么特别强调向量的原因所在.

回应文章开头所引的陈省身先生的访谈，关于向量在高中教材中可能的渗透，我们推荐有兴趣的读者参考项武义教授的著作[7]，在该书第六章的引言中，他对向量有一段精彩的评论，我们引来为本文做结：“如今反思回顾，可见向量代数其实乃是坐标几何的返璞归真、精益求精，它使得几何和代数结合得更加真切自然、直截了当……这种返璞归真的向量减法，可以把解析几何的精要体现得更加简明朴实.”