“平面”教学设计的理性突围
——兼谈原始概念的教学
胡 浩
(安徽省芜湖市沈巷中学 241012)
1 作图教学中产生的困惑
“平面”是几何学中的原始概念,是高中数学帮助学生建立空间观念、培养空间想象能力及空间认知能力的“第一粒钮扣”.但在教学实践中,教师通常不重视此概念的教学,表现在只是通过类比直线,借助“平静的水面”、“光滑的桌面”等物象展开告知式的教学,过高地估计学生的原有认知基础,导致后续的作图教学遇到了瓶颈:学生不能顺畅地作出两个平面的交线,进而不能画出几何体中符合要求的截面,更不能解决诸如多面体各面延伸分空间部分问题.章建跃博士曾说:“作图是立体几何学习的‘第一大事’”; 2017年6月,代钦教授在北京师范大学举行的“中学数学课程与教材国际论坛”上,也指出:“作图是几何教育的根基.”如何把数学想清楚,如何把数学讲明白,如何使学生会思考,这是数学教师专业素养和教学睿智的刚性要求.基于此,笔者通过调研,得出:其根源还是学生对平面及其性质,尤其是对平面“无限延展性”理解不到位,进而表明传统的教学设计或大多数设计,对学情的分析有偏差,目中有人,但影像模糊,偏离了教学的宗旨——成就和发展学生.
2 平面的意象和认知基础
学习立体几何,学生对平面的意象主要是生活实践、旧有知识中的物象,显性认知是直线,而隐性的认知是研究几何对象的思想.
(1)从概念意象上看,主要是学生无意识积累的一些关于平面的生活类、旧知类和图形类的初步认识[1],如:平静的水面、光滑的桌面,长方体、正方体的面,等.
(2)从知识基础上看,主要是学生关于直线的知识(定义、表示、直线公理等),主要基于学生对直线“无头无尾”性质的想象与理解.
(3)从研究思路上看,研究一个几何对象,有一条“惯常线路”:先是结合生活实际,抽象出几何对象,然后下定义,用文字语言、图形语言、符号语言表示对象;接下来研究其性质,主要是构成图形的一些要素之间的关系,包括位置关系、数量关系、与其它几何对象的关系等.这条线路,学生虽已多次体验,但未加留意,也未必熟悉.这取决于教师的教育理念,取决于教学活动的宽度与高度,取决于教学行为的品位与品质,在平时的教学中教师是否注重对学生进行“系统思维”的历练和养成.
3 传统教学设计及其弊端
在各级各类考评课、优质课、示范课、公开课中,“平面”的教学设计大体框架如下:
(1)回顾直线的概念(生活抽象,特征:直的、无限延伸、没有长短、没有粗细),类比得出平面的概念(平的、无限延展性,没有边界、没有厚薄).
(2)类比直线的画法与表示,让学生自主学习:读一读,画一画,写一写,说一说,得出平面的画法与表示.
(3)结合学具(直线、平面),提炼出直线在平面内、平面与平面重合、平面与平面相交这三种位置关系,从公共点的个数或分布规律,多媒体辅助,展开三个公理的教学.
物质的本质是运动.笔者认为,根据这样的设计展开平面概念的教学,学生得到的只是静态的、僵化的、没有迁移能力和发展潜力的知识,不能真正突破平面无限延展性的“围堵”,有明显的弊端或不足.
学生对“平面”的认知基础和意象主要来自直线,但是,由于学生对直线的理解只是停留在“一维”区间中,不能升级到“二维”域的层面,因而导致传统教学设计表面芳华,却不能生根.事实上,由直线类比出平面,需要舍弃对象所有的物理性质,抽象出对象的数学属性(即把对象数学化),需要学生有很强的空间想象能力和数学直觉思维能力,这对大多数学生来说,思维跨度太大,能力要求过高.另外,“平静的水面”、“光滑的桌面”等物象,只能形成学生平面“平”的形象,不能形成学生平面“无边”的意象,反而容易产生平面“是有边界”、“是个封闭图形”的思维干扰.教科书中,“用平行四边形表示平面”的说法,实属不妥,应调整为“用平行四边形表示平面的局部”,实际上,平面是不可以画出全貌的,这就给研究空间中点、线、面之间的位置关系带来很大不便.如何解决?用平行四边形表示平面的局部,再辅以平面具有“无限延展性”的想象,问题迎刃而解.基于此,笔者又查阅了一些经典的教学设计文献,大体上按以上设计展开教学.笔者沉思,平面的教学设计难道就是如此的固步自封,自我囚禁,不能与时俱进?一定不是,传统的教学设计必须要革新.
4 创新设计实现理性突围
化学家傅鹰指出:“一门科学的历史是那门科学最宝贵的一部分,因为科学只能给我们知识,而历史却给我们智慧”.平面的概念在历史上经过了漫长的发展,众多数学家都对平面作过刻画.[2]
古希腊哲学家巴门尼德(Parmenides)将平面定义为“一个二维对象、直的表面.”
欧几里得(Euclid)将平面定义为“与其上直线一样平放着的面.”
海伦(Heron)将平面定义为“平面是具有以下性质的面,它向四周无限延展,平面上的直线都与之相合,且若一条直线上有两点与之相合,则整条直线在任意位置与之相合.”
傅里叶(Fourier)对平面的定义为“平面由经过直线上一点且与直线垂直的所有直线构成.”
莱布尼兹(G.W.Leibniz)将平面看成“平面是与两点等距离的点的集合.”
数学史是教学的指南,教育取向的数学史研究为课堂教学提供了丰富的素材.通过回顾历史,我们不难发现:平面的认知基础和意象的确是直线.但是,采用告知式的教学方式,显然不能对学生进行数学研究方法的渗透,不能对学生进行理性精神的培养.因此,立足教材,着眼学生,对平面的教学进行创新设计意义重大.
(1)回顾直线的概念.生活抽象,特征:直的、无限延伸、没有长短、没有粗细.教师指出,描述直线概念时,我们是舍弃了其物理性质:粗细、轻重、颜色等,保留其数学属性:直的、无限延伸,因而直线是没有长短的.
(2)由“平静的水面”、“光滑的桌面”等物象,抽象出“平”的形象;用几何画板动态展示,历史上数学家傅里叶对平面的理解:“平面由经过直线上一点且与直线垂直的所有直线构成.”如图1.
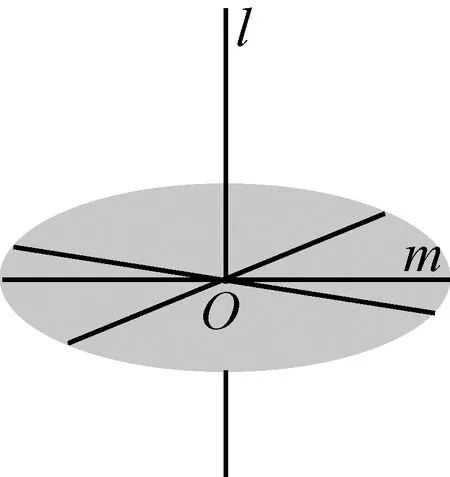
图1
(3)结合几何画板的动态演示,引导学生思考、探究和感悟:直线m在转动过程中,由于始终与直线l垂直,再加上m是直的,所以直线m扫过的图形应该是“平的”;又因为直线m是无限延伸的,无头无尾,因而其运动产生的图形应该是“无限延展的”,无边无际.在还原数学家傅里叶探究平面概念之旅的过程中,学生的形象思维与抽象思维能力,几何直观意识与数学理性精神,得到一次刻骨铭心的历炼,数学核心素养受到一次扎实有效的培育.在抽象出平面“平的”、“无限延展的”的特征之后,我们可以用怎样形象化的语言来描述平面呢?——“无边无垠”、“坦荡如砥”!
(4)引导学生对平面进行小结:点动成线,线动成面.平面是:平的,无限延展、没有边界、没有大小,没有厚薄.教师指出,描述平面概念时,我们是舍弃了其物理性质:厚薄、轻重、颜色等,抽象其数学属性:平的、无限延展,因而平面是没有边界的,其面积是不可求的.
(5)类比直线的画法与表示,让学生自主学习:读一读,画一画,写一写,说一说,得出平面的画法与表示.教师强调,用平行四边形表示的只是平面的局部,但是却为我们研究空间图形的结构和性质带来很大的方便.
(6)结合学具(直线、平面),提炼出直线在平面内、平面与平面重合、平面与平面相交这三种位置关系,从公共点的个数或分布规律,多媒体辅助,展开三个公理的教学.为什么两个平面只要有一个公共点,那么它们就有且只有一条经过该公共点的公共直线?“无限延展性”必然导致两平面“相交”,“平的”则保证交线“有且只有一条”.
孔凡哲、史宁中教授认为:“培育学生的数学核心素养,需要教师帮助学生亲身经历数学化的过程,获得理解性掌握,在获知过程中提升数学核心素养.”章建跃博士进一步指出:“当前,在几何教材中落实数学核心素养,就是要在‘何由以知其所以然’上进行突破与创新.”[3]要使学生对平面的概念获得理解性掌握,就必须要创新教学设计.平面的教学不但要建立在生活以及旧有知识的基础上进行,而且又要考虑融入数学史的角度进行教学[1].借助信息技术直观形象的演示功能,添加数学史素材,能有效地刺激学生大脑的沟回,激发学生的形象思维和抽象思维;能够十分有效地化解“无限延展性”的学习障碍,实现由平面意象到平面形象,再到平面意境,直到平面概念的精准落地与华丽转身.
5 原始概念教学价值取向
“把握数学本质,启发思考,改进教学.”是《普通高中数学课程标准(2017版)》四大基本理念之一.新课标要求普通高中数学课程要以发展学生数学学科核心素养为导向,创设合适的教学情境,为学生的可持续发展和终身学习创造条件.数学教学不仅要关注如何帮助学生学会知识、技能、思想、方法,更应当关注如何引导学生会学习、会思考、会应用,不断引导学生感悟数学的科学价值、应用价值、文化价值和审美价值.
在数学核心素养“六核三观”的引领下,除了单纯的知识与技能的习得,学生还需要拥有“在特定情境中,能够运用包括知识、技能与态度在内的心理的、社会的资源,应对复杂问题的能力.”要培育这种创新能力,意味着以知识传授为主体的课堂教学范式需要转型,从“知识本位”的被动地应试学习,转型为“素养本位”的能动地深度学习.
概念是数学的桩基.要从总体上理解数学,必须要构建概念的结构体系,结构体系不仅是知识之间的链接,也是数学知识与学生认知之间的链接.核心概念的教学既要解构也要建构,解构为的是帮助教师把握数学的本身;建构为的是帮助教师将数学传授给学生.这是建立结构体系的两个基石[4].
原始概念的教学,其流程导图一般如图2所示.
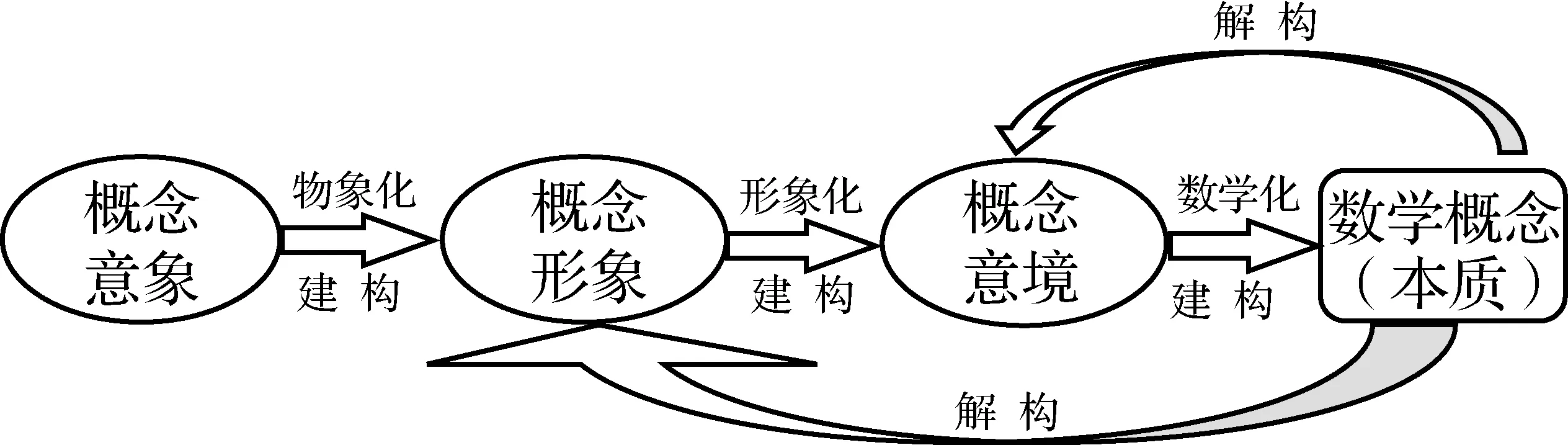
图2
原始概念的教学,其模式一般有两种:一种是基于学科本身,围绕“教”而谋;一种是基于教育对象,围绕“学”而做.基于数学核心素养观的原始概念教学,要把师生的教学活动当作一个有机整体,双管齐下,多点联动,而不是将 “教”与 “学”各作一方来处理.原始概念的教学也是师生为实现教学任务和目标,围绕教学内容,共同参与,通过对话、沟通和合作活动,产生交互影响,以动态生成的方式推进教学活动的过程.首先,从课程的角度来看,概念教学要厘清其“前世今生”,探究的内容要有价值,要贴近学生,利于学习;其次,从教学的角度来看,要搞清楚学生在形成概念,吸纳知识、方法和思想时,可能的困惑点及其成因.学生已经理解了什么,学生不理解的怎么处理,讲解到什么程度,教师要有应对的策略;再次,从教师的角度来看,完成概念教学要有哪些知识储备,具备哪些专业素养、教学技术和教育艺术,教师要先知先觉,胸有成竹.
原始概念的教学,要遵循其产生发展的历史,教学过程必须符合学生的认知规律,顺应人性的发展.要探究原始概念生成的过程,讲解描述性语义背后的“故事”,重温概念产生的文化场景,揭示概念的结构与本质.防止由于泛化的类比和直白的告知,导致学生对概念的理解产生“飘移”,而不得不采用大量重复的练习,来对概念的理解和应用进行锚定.原始概念的教学是“慢”的艺术,讲究“焐”的过程,走走停停,想想探探,会看到更多的瑰丽风景.
原始概念的教学,更要进行创新设计,可以作为“主题教学”的素材,指导学生模拟微科研进行“项目研究”,收集、阅读相关的历史资料,结合其发展过程撰写研究报告.从数学的历史中寻找智慧,运用信息技术、画图软件甚至人工智能,获取各种相应的教学资源,利用可视化数据处理的方法和技术,及时分析概念教学中的各种案例和问题,实现概念理解的理性突围.原始概念的教学,不仅考验教师的专业素质和教学水准,体现教师反思研究的能力,而且又能培养学生发现问题、分析问题和解决问题,进行科学研究的实践能力.
原始概念教学的背后,是教师对教育的感悟,是对数学的把握,是对教学的理解,是对学生健康成长方式的认识.学习即体验,成长即经历,让我们以理念浸润设计,用智慧点亮课堂,为学生成长而教!

