物块沿斜面下滑时间问题探讨

邹兆贵

(长沙市长郡滨江中学 湖南 长沙 410013)

高中物理教学当中，经常会遇到求物块沿斜面下滑所用时间的问题．通常斜面固定不动，由牛顿运动定律能够快速求解物块沿斜面下滑的加速度，从而求出下滑所用时间．鲜见针对斜面不固定时(斜面与水平面存在摩擦)物块沿斜面下滑所用时间的问题，本文就此做一般论述．

1 问题描述

如图1所示，一质量为M的斜面静止在水平面上，斜面倾角为θ，斜面总长为L，M与水平面之间的动摩擦因数为μ．把一质量为m的物块从斜面顶端无初速度释放(物块与斜面之间接触面光滑)，求物块经过多长时间t滑到斜面底端．(假设斜面与水平面之间的最大静摩擦力等于滑动摩擦力)

图1 题图

2 问题分析与解答

如图2所示，设物块从斜面顶端下滑到图2所示位置时刻，斜面的水平加速度大小为a1，斜面对物块的支持力为Fn．物块对斜面的压力为Fn1，水平地面对斜面的滑动摩擦力为Ff．地面对斜面的支持力为Fn2．以水平面作参考的惯性系中，对斜面,水平方向上有

Fn1sinθ-Ff=Ma1

(1)

竖直方向上有

Fn1cosθ+Mg=Fn2

(2)

由滑动摩擦力公式知

Ff=μFn2

(3)

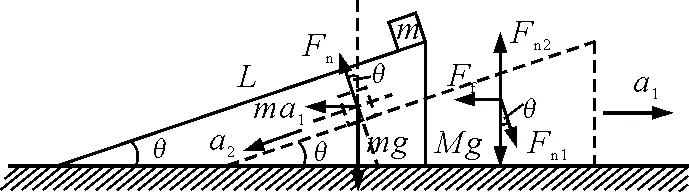
图2 分析图

对物块，以斜面作参考的非惯性系中，物块相对于斜面的加速度方向沿斜面向下，用a2表示物块相对于斜面的加速度，引入惯性力-ma1，对物块,沿斜面方向

mgsinθ+ma1cosθ=ma2

(4)

垂直斜面方向

ma1sinθ+Fn-mgcosθ=0

(5)

由牛顿第三定律知

Fn=Fn1

(6)

由式(5)得

Fn=mgcosθ-ma1sinθ

(7)

把式(6)、式(7)代入式(2)得

Fn2=mgcos2θ-ma1sinθcosθ+Mg

(8)

把式(3)、(6)、(7)、(8)代入式(1)得

mgcosθsinθ-ma1sin2θ-

μ(mgcos2θ-ma1sinθcosθ+Mg)=Ma1

(9)

由式(9)得

(10)

把式(10)代入式(4)得

(11)

当μ，g，θ，m，M均为定值时，由式(11)易知a2为定值，故物块相对斜面沿斜面向下做初速度为零的匀加速直线运动．在以斜面作参考的非惯性系中，对物块，由运动学公式知

(12)

联立式(11)、式(12)得

(13)

设斜面与水平面之间的动摩擦因数为μ0时，斜面相对于水平面刚好要滑动．此时a1=0，代入式(10)得

a1=0

斜面保持静止，把a1=0代入式(4)得

a2=gsinθ

把a2=gsinθ代入式(12)得

物块相对斜面下滑的加速度为

物块下滑至斜面底端用时

特别地，当μ=0时

计算结果与文献[1～6]一致．

此时

3 结束语

物块沿斜面下滑所用时间问题，关键在于求解物块相对于斜面的加速度．斜面不固定时(斜面与水平地面存在摩擦)，对物块取非惯性系斜面作参考系，引入惯性力能够方便求解物块相对于斜面的加速度大小．此类问题综合涉及了受力分析、牛顿运动定律、惯性系与非惯性系，可以作为一个很好的研究非惯性系中物体相对运动的实例．