柱式负荷传感器的摆动支承振动分析

赖朝晖，杨晓翔，2，姚进辉，赖征创，

（1.福州大学 机械工程及自动化学院，福州 350116；2.泉州师范学院，福建 泉州 362000；3.福建省计量科学研究院，福州 350003）

柱式负荷传感器是轴组式动态汽车衡的重要组成部件，放置于称重秤台和地基基础之间，起着承载和称重的作用[1]。在动态称重系统中，柱式负荷传感器必须采用能适应一定周期变形的弹性体元件。用得较多的支承结构有两种，一种是能提供回复力的摆动支承结构，这种结构把称重传感器作为摆动结构中的一个组成部分，另一种结构是弹性的支承结构，由弹性体元件承担补偿和阻尼的作用[2]。利用物体的摆动效应来实现某些需要的例子有很多，除了动态称重外，如Xianzhi Dai利用旋转摆的力学效应，设计了某种振动能量采集器，利用旋转摆的非线性振动与磁电式传感器输出的相关性分析振动能量采集器的宽带倍频特性[3]。Ciornei M C等给出了物体直线滚动的摩擦力和滚动阻力的表达式和纯滚动下滚动角度与相关参数的一般关系式，设计了一种由两个球体支承的实验装置，方法是让球体在所研究的材料上滚动，在杆上施加重量来调整单摆的惯性特性，通过测量摆动振幅等参数求得滚动阻力系数，并得出滚动阻力系数影响振幅而不影响振动频率的结论[4]。Igor Gilavdary等分析了由两个球头摆动支承的单摆在一个平面上滚动的自由摆动以研究滚动摩擦的实验装置，给出其摆动支承的稳定性条件，并提出两预轧制球头摆动支承的单摆微幅自由摆动的动力学机理和能量耗散机制[5]。

柱式负荷传感器摆动支承结构在称重过程中，不可避免地产生摆动，这种摆动将导致被称物体重力方向不再沿着负荷传感器的轴线方向。陈俊翔等对这种偏离轴线的荷载产生附加弯矩和侧向力等寄生分量进行了实验研究，得出附加弯矩是传感器方位误差产生的重要原因[6]。Peters M等人在做了大量的比对试验后发现，力的非轴向分量及附加弯矩是造成方位误差的直接原因[7-8]。

本文针对摆动支承柱式负荷传感器的称重过程进行受力分析，在动态称重系统中，选取轴组式动态汽车衡测轴重为研究对象，分析轴载工况，通过MATLAB/Simulink软件进行动力学系统建模与仿真得到称重系统的动态响应。

1 摆动支承的稳定性分析

摆动支承柱式负荷传感器由中间部位的应变弹性体和上下压头组成[2]。下压头固定于基础上，与应变弹性体点面接触，弹性体上下端部为球面，可在上下压头上滚动。上压头与秤台固定连接，底面与应变弹性体点面接触，其运动状态如图1所示。

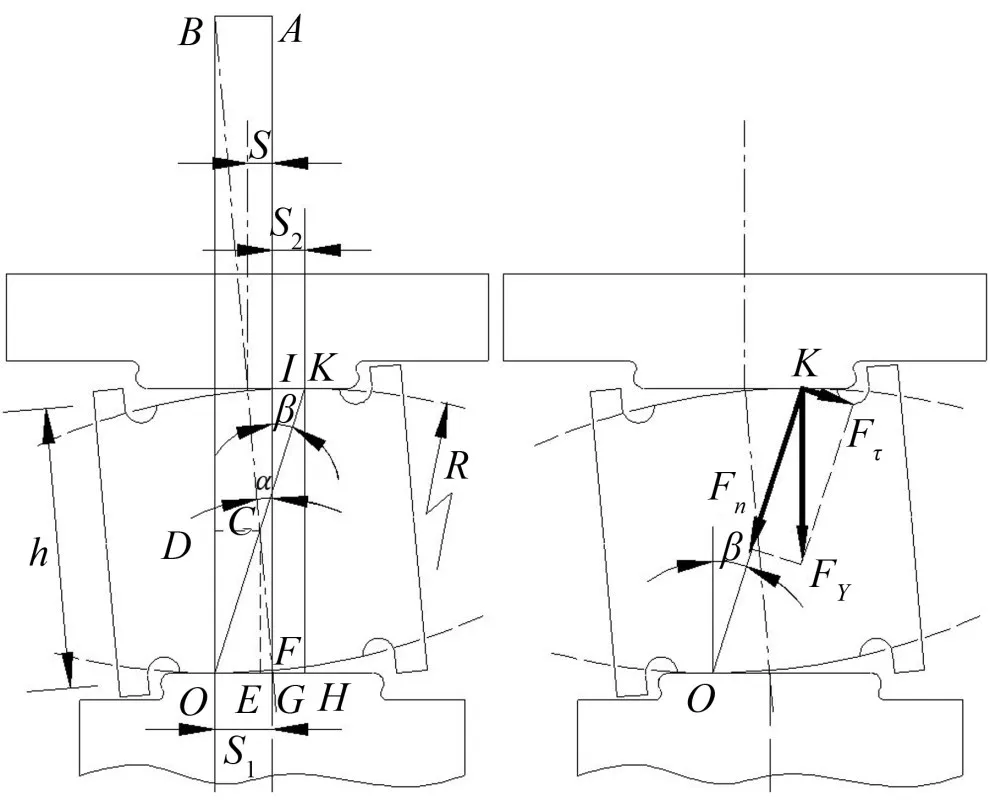
图1 称重传感器的摆动支承图

当传感器弹性体做纯滚动时，下压头固定不动，而上压头随着弹性体接触点位置的瞬变做平动。令A、B两点为弹性体下端球头滚动前后的圆心，C点为弹性体的形心，根据图中各尺寸的几何关系，有

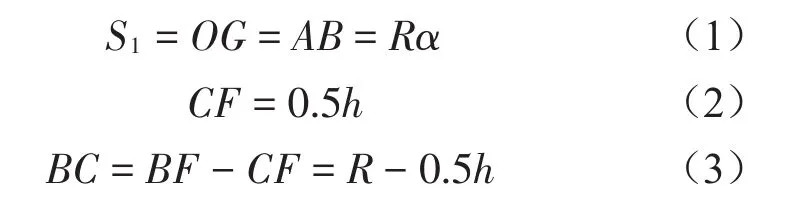
式中：

α为传感器应变弹性体轴线倾角；

h为传感器应变弹性体沿轴线的高度；

β为球头和上压头接触点与滚动点连线的倾角；

R为球头半径；

S为上压头的轴线水平偏移位移；

S1为球头与下压头接触点的滚动位移；

S2为球头与上压头接触点的水平移动距离。

这里直接由几何关系和力矩效应判定摆动支承稳定性条件，当β＞0时，上压头对弹性体的竖向力能使弹性体回摆到平衡位置的作用[9]。由式(10）可知2R＞h是摆动支承的稳定平衡条件，这与用最小势能法求得的稳定平衡条件一致[10]。

对于稳定平衡的摆动支承，这时被称物体对弹性体的竖向力可分解为沿上压头转轴的径向力Fn和切向力Fτ，其中切向力Fτ提供摆动支承振动的回复力促使结构稳定。当系统为微幅摆动时

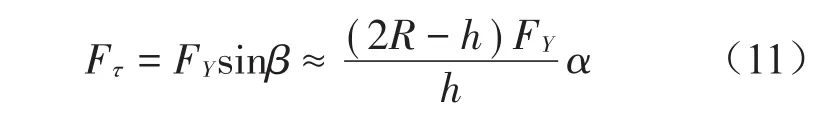
由上式可知，微幅摆动支承的回复力与摆动角度和外界施加的竖向力近似成正比关系。

2 摆动支承振动的动力学模型

轴组式动态汽车衡由四个柱式负荷传感器作为承载器，车辆沿秤台纵向轴线行驶时，秤体只沿秤台纵向振动，为单自由度系统，由式（11）可知，其摆动刚度近似与每个传感器所受外载及偏移角度成正比，其摆动支承振动的动力学模型如图2所示。设MO（fii=1、2、3、4）为弹性体与下压头的滚动摩阻力偶，在滚动过程中，滚动摩阻力偶矩近似等于Mmax，最大滚动摩阻力偶矩与下压头支承点所受的竖向压力FOYi的大小成正比，令比例常数为δ，即

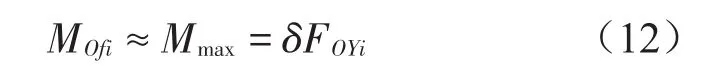
将外载对秤台的作用力向秤台顶面简化为侧向力FGS，竖向力FG和力偶矩MGf。秤台与传感器弹性体间的相互作用可视为点面接触的简支板结构，弹性体在接触点K只受秤台竖向力FNi、水平摩擦力FXi和滚动摩阻力偶MKfi的作用。同理，有

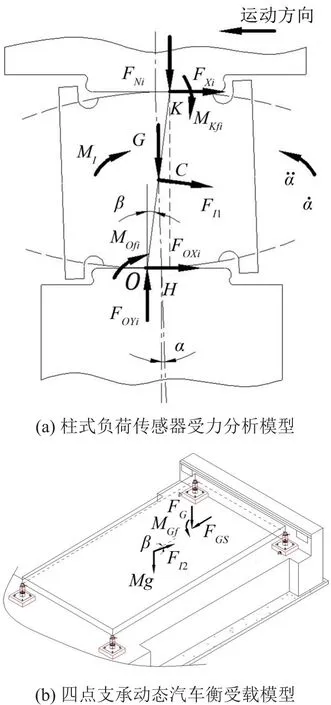
图2 摆动支承振动状态动力学模型

由于秤体是一个整体，每个柱式负荷传感器的摆动角度和方向与秤台始终一致，这时，称重系统的总刚度等于各并联柱式负荷传感器的摆动刚度之和。而各柱式负荷传感器在摆角相同的静止状态下，摆动刚度正比于竖向力，设比例系数为C，则有

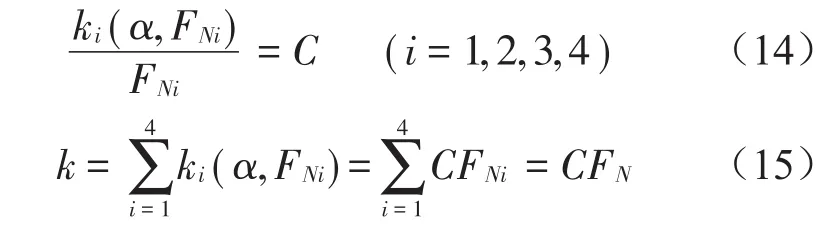
由（15）式可知，车辆在秤台上行驶时，虽然作用在各柱式负荷传感器上的力发生瞬变，但各传感器的支承振动与秤台的振动同步，各传感器所受外力之和保持不变。

以4个柱式负荷传感器为研究对象，由拉格朗日形式的达朗贝尔原理，将柱式负荷传感器对支承点O取力矩平衡，叠加其余3个负荷传感器对其各支承点取力矩平衡的方程式后，可得称重系统摆动支承振动的动力学控制方程

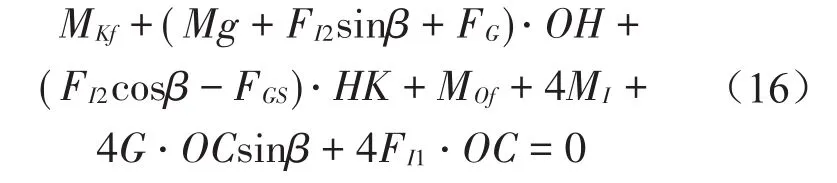
式中：

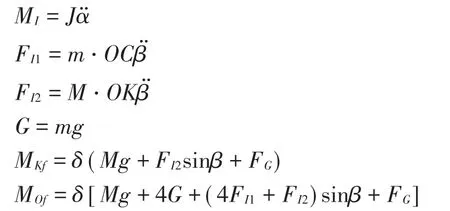
m为弹性体质量；

M为秤台质量；

J为弹性体的转动惯量。

根据球头与上、下压头间的滚动摩阻力偶矩总是阻碍弹性体的相对滚动，方向与弹性体滚动角速度̇的方向相反，起到阻碍弹性体滚动的作用而做负功，接触点处静摩擦力在纯滚动过程中并不做功。类似库伦阻尼对弹簧振子弹性势能的耗散作用[11]，自由振动将逐渐稳定在平衡位置附近。将相关参数代入式（16），得系统摆动支承振动控制方程

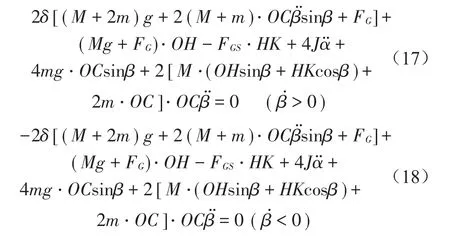
令ω0=，引入下列无量纲参数

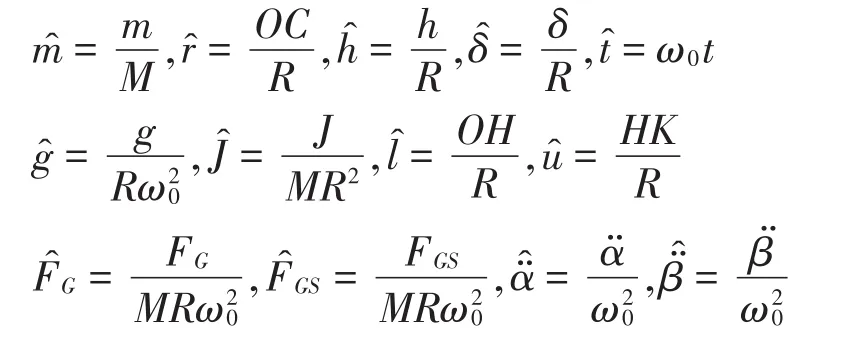
无量纲化后，动力学控制方程为

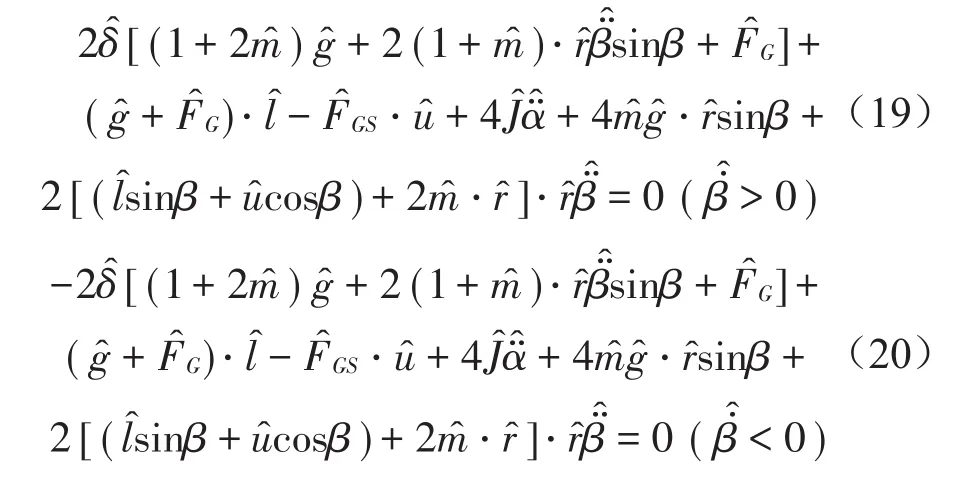
3 汽车衡动态称重下轴载工况分析

3.1 车辆在道路路面行驶时的轴载工况分析

设被称车辆为后轴驱动的载重货车，轴型为前轴和并装双轴的后轴组成，且FG2=FG3，轴载和轴距如图3所示。

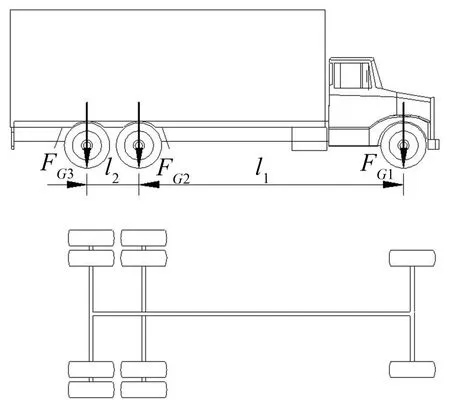
图3 载重货车轴载和轴距示意图

设车辆在道路路面行驶时，在驱动力的作用下做加速纯滚动运动，驱动轮受到驱动力矩、向后的牵引力反力、竖直向下的轴载、地面的摩擦力和滚动阻力，从动轮不受驱动力矩作用，设从动轮的牵引力方向向前，自由滚动时不受驱动力矩和牵引力的作用。

以各轴为研究对象，将单个轴的所属轮胎进行整体考虑，设各轴力的方向和加速度方向如图4（a）、（b）所示，根据图中纯滚动圆轮静摩擦力的方向，用平面运动微分方程确定其静摩擦力的大小[12]，有

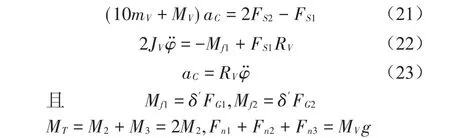
式中：

MV为车身质量；

mV为单个轮胎质量；

F为汽车对前轴牵引力；

JV为轮胎转动惯量；

δ´为车轮与秤台面的滚动摩阻系数；

RV为轮胎半径；

MT为后轴总驱动力矩；

为轮胎滚动角加速度。

联立方程式（21）－式（23）解得

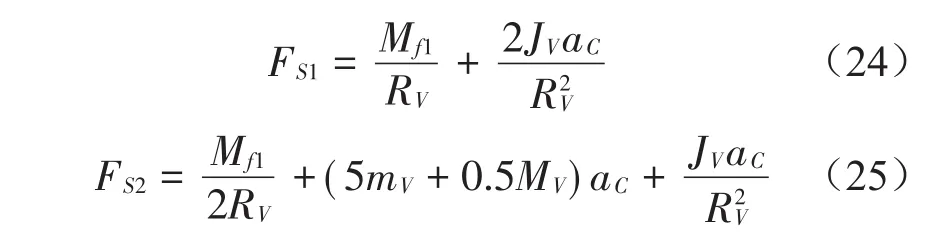
同理，对于匀速运动的纯滚动状态，如图4（c）所示。

驱动力等于静摩擦力，即F=FS1，由平衡关系可得

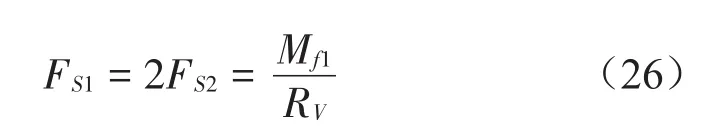
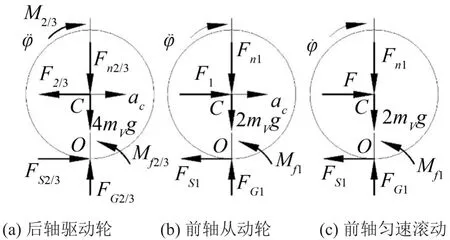
图4 车轮纯滚动受力分析

3.2 车辆在秤台上行驶时的轴载工况分析

为确定柱式负荷传感器摆动支承受迫振动的外界干扰力，这里选取轴组式动态汽车衡称重系统为研究对象。四点支承的秤台在车辆冲击的作用下做变速运动，以车辆行驶方向为正方向，车辆某个轴的轮胎在秤台上纯滚动时，其车轮的角加速度为

其余轴行驶在道路路面上的轮胎滚动角加速度和轮心平动加速度的关系同式（23）。同理，通过对各轴列平衡方程，可分别求出车辆通过秤台时各轴所受的静摩擦力大小。

4 数值计算

为求得柱式负荷传感器摆动支承的振动响应解，这里选取轴组式动态汽车衡称重过程下，秤台与传感器的响应为研究对象，分别选取无车辆行驶时，称重系统摆动支承的自由振动和受车辆动载时的受迫振动进行MATLAB/Simulink仿真。

4.1 摆动支承自由振动的数值仿真

考虑到弹性体的球头半径影响柱式负荷传感器偏载的称重准确度，这里仅分析可作调整的弹性体高度对摆动支承振动状态的影响。

为排除其它影响因素，设摆动支承为自由振动，不受车辆荷载影响，即FG、FGS、MGf均为0。选取柱式负荷传感器C16AC3操作手册中最大量程为20 t的称重传感器参数。设初始角位移α0=0.01 rad，初始角速度为0，弹性体与上、下压头的滚动摩阻系数按理论力学所给的钢质车轮与钢轨间的系数，相关参数如表1所示。

由于M≫m，当α角较小时，可忽略负荷传感器弹性体的质量和转动惯量，且sinα≈α，cosα≈cosβ=1。上述参数无量纲化后，代入式（19）、式（20）可求得摆动支承振动在初始角位移α0=0.02 rad，初始角速度为0的条件下的自由振动解，振动曲线如图5所示。

由图5可知，随着弹性体高度的降低，摆动支承振动的回复时间减小，振幅增大，振动衰减时间也越长。

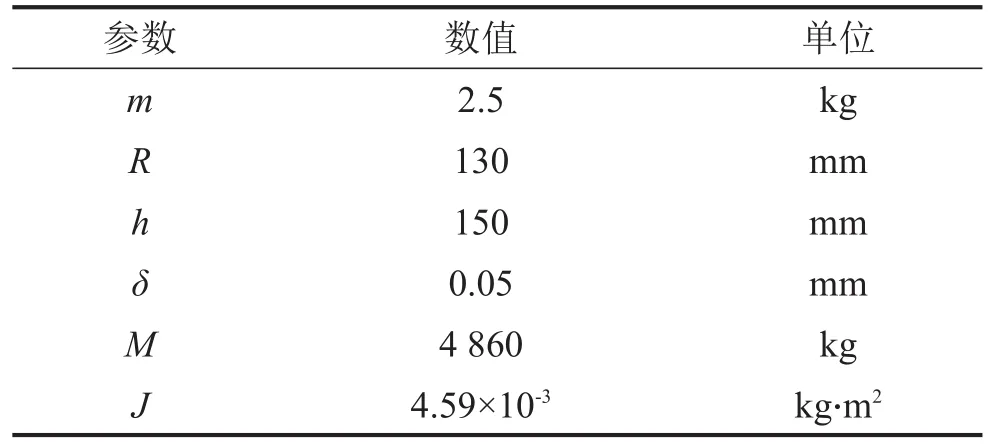
表1 摆动支承自由振动参数

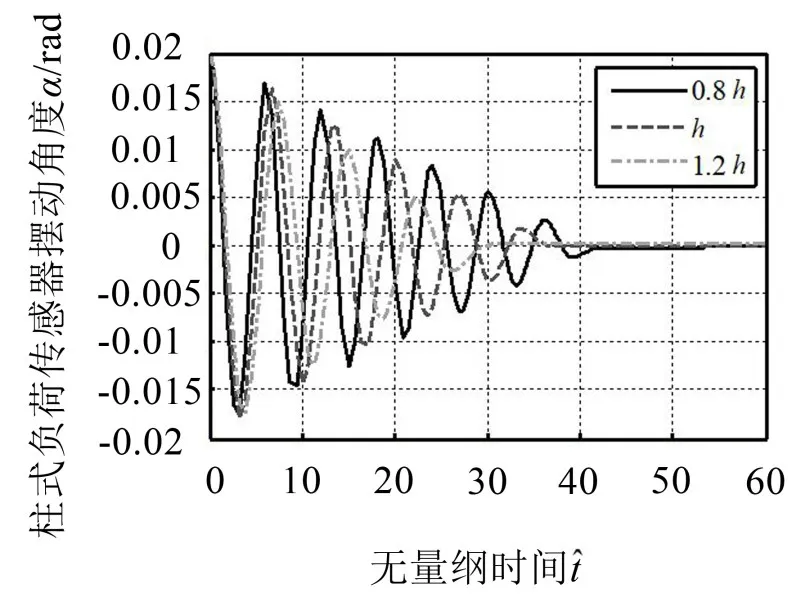
图5 摆动支承自由振动的数值仿真曲线图

4.2 摆动支承受迫振动的数值仿真

受迫振动时，设称重系统处于平衡状态，初始角位移α0和初始角速度均为0。选取东风DFL1250A6载货汽车（1+5型）为施加轴载的后轮驱动车辆，后轴为并装双轴，轴载和轴距如图3所示，车轮轮胎为子午线宽轮辋轮胎，轮胎规格为10.00R20，轮胎半径为RV=527 mm。车轮与秤面的滚动摩阻系数取中间值δ´=6 mm，其它相关参数如表2所示。

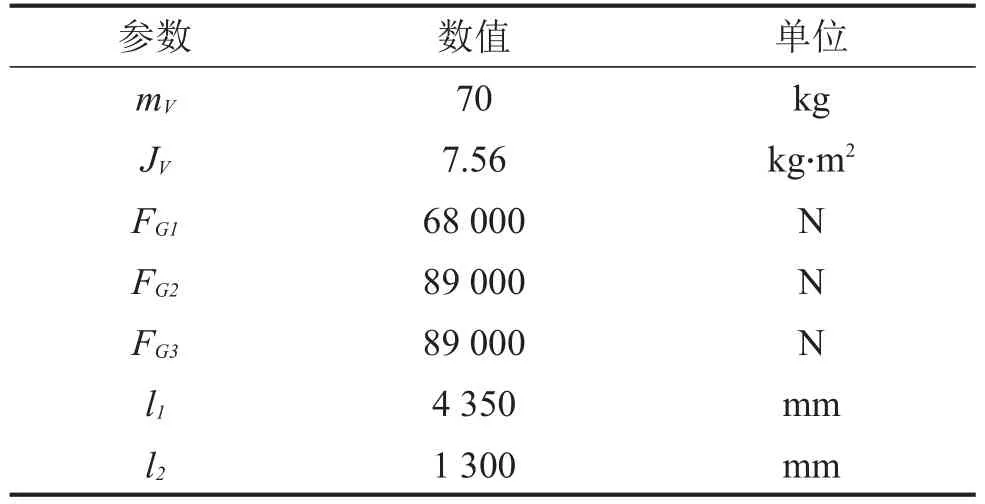
表2 摆动支承受迫振动参数

设被称车辆以v=2 m/s的速度匀速驶过秤台，则aC=0。以下只求解行驶在秤台上的轴载，由式（27）得行驶在秤台上的车轮角加速度

则由匀速滚动静摩擦公式（26）及式（28），得前轴行驶在秤台上时静摩擦力

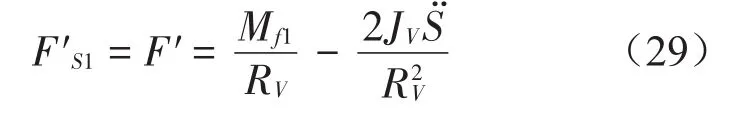
当前轴在秤台上时，后轴静摩擦力

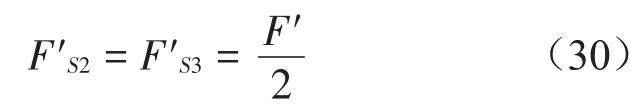
当前轴驶出秤台后，后轴静摩擦力

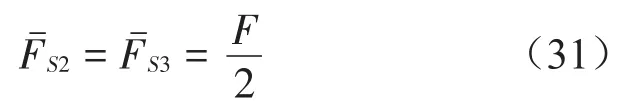
取秤台长度为5 250 mm，根据车速和轴距可得车辆在秤台上的行驶过程。当车辆刚上秤时，设t=0，则此时秤台上仅有前轴在秤台上施加荷载，到第二轴施加荷载的时间间隔为

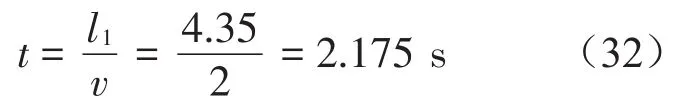
施加到秤台上的总竖向力FG=FG1，总摩擦力由式（29）得FGS=F′S1，滚动摩阻力偶MGf=δ´FG1，同理，可求得其余时间段施加到秤台上的车轴载荷的变化过程，如表3所示。

表3 不同时间段秤台受载工况

同样，考虑M≫m，当α角较小时，可忽略传感器弹性体的质量和转动惯量。代入以上给定参数，可求得摆动支承振动在初始角位移α0和初始角速度均为0，汽车在匀速行驶的条件下的受迫振动解，振动曲线如图6所示。

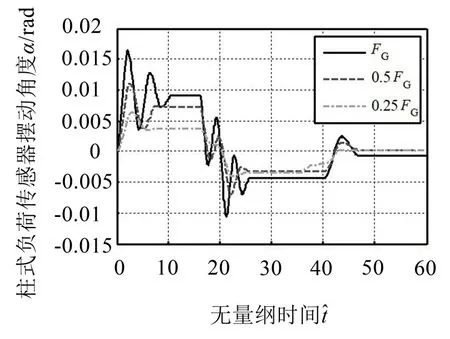
图6 摆动支承受迫振动的数值仿真曲线图

从图中可知，随着轴载的增加，振动越显著，振动回复时间越快，振幅越大，振动衰减时间越长。从图7可知，提高秤台表面的平整度，减小滚动摩阻力偶以减小车轮与秤台间的水平静摩擦力能显著地降低摆动支承振动的振幅，因水平静摩擦力远小于竖向重力，故振动回复时间几乎不变，振动的衰减时间也越短。

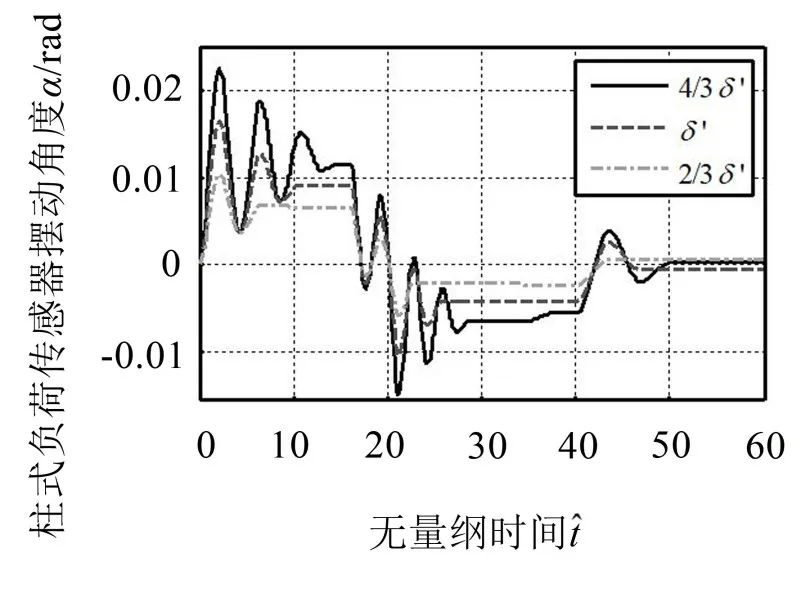
图7 摆动支承受迫振动的数值仿真曲线图

从图6可看出，当车辆匀速通过秤台时，水平静摩擦力对秤台的冲击造成的振动比较小，但是，当车辆在秤台上启动、加速或刹车时，将对秤台造成比较大的冲击，引起秤台的剧烈振动。振幅较大时容易对称重产生不稳定影响，实际应用中，多采用顶撞式限位或拉杆式限位[13]。秤台限位装置与基础预埋钢板碰撞后速度变小，确保秤台晃动幅度在规定范围之内。取弹性碰撞的恢复因数为0.56，限位螺栓与纵向限位板之间的距离为Smax=5 mm，即αmax=0.033 3 rad，如图8所示。

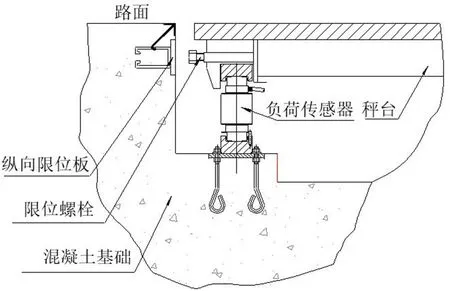
图8 螺栓顶撞式限位结构图

为了分析限位振动下的速度变化情况，引入无量纲角速度

在表2所给参数条件下，设车辆刚驶入秤台时弹性体摆动的初始条件为α=0，=0.2，支承振动的摆动角度和无量纲角速度变化情况如图9所示。

从图9可以看出，秤台限位螺栓与纵向限位板共碰撞了4次，碰撞后，振动速度大大减小。当滚动摩阻系数δ较小时，过大的摆动支承振动衰减较慢，通过限位装置消耗振动的能量可以大幅减少振动的振幅，避免过大的摆动角度影响称重系统的称重准确度和结构稳定性。

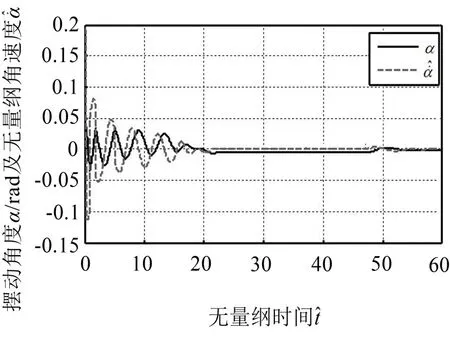
图9 顶撞式限位振动仿真曲线图

5 结语

摆动支承柱式负荷传感器在动态称重过程中，表现出振动特性，影响称重稳定性和准确性，甚至影响称重传感器的疲劳寿命。本文研究的结论可用于分析负荷传感器摆动支承振动的动力学过程及对称重精度的影响，可为相应的振动控制或减振设计提供依据。得出的主要结论有：

(1)支承振动回复力近似与振动角位移和载重量成正比；

(2)称重系统摆动支承振动的回复时间随着弹性体高度的降低而减小，振幅随弹性体高度的降低而增大，振动衰减时间随弹性体高度的降低而增大，秤体水平晃动产生的噪声干扰频率会影响称重数据处理，在满足称重精度的条件下，可适当提高弹性体高度以减小振动回摆速率和振幅；

(3)秤台水平支承振动刚度与秤台所受荷载的大小相关，而与荷载的分布位置无关，随着轴载的增加，振动回复时间减小，振幅增大，振动越显著，振动衰减时间也越长，一般采用限位装置来限制和消耗秤台的振动；

(4)在满足防滑的条件下，应提高秤台表面的平整度，减小滚动摩阻力偶以减小车轮与秤台间的水平静摩擦力能显著地降低摆动支承振动的振幅，而振动回复时间几乎不变，同时振动的衰减也越快；

(5)选用限位装置来限制秤台的振动，可以有效地降低冲击造成的过大振幅，限制传感器弹性体的摆动幅度，这可以提高称重系统的结构稳定性和称重准确度，减小外界对传感器的疲劳荷载。