基于“灰度不减”公理的改进区间灰数预测模型

李 翀，谢秀萍

（福州大学 经济与管理学院，福州 350116）

0 引言

灰色系统理论的研究对象之一是灰色预测模型，其中，GM(1，1)模型又是灰色预测理论的基础模型。目前关于GM(1，1)模型的研究主要是从模型的性质以及适用范围[1,2]，背景值构建[3,4]；初始值选择[5,6]；与其他算法的组合[7,8]；引入时间项[9,10]；建模序列的优化[11,12]；模型求解[13]等。GM系列模型是以确定数据为建模序列，无法直接对含有不确定数据的序列进行有效建模。随着信息复杂性的增长，具有不确定特征的序列已随处可见，这类的数据序列进行建模已引起众多学者的关注。根据建模序列数据类型可以分为两种：区间灰数序列预测[14-17]和灰色异构数据序列预测[17,18]。其中区间灰数序列建模方法主要有：（1）基于序列的几何特征[14,15]；（2）基于序列的表征信息[16,17]；（3）组合模型[17,18]等。目前，无论是区间灰数序列还是异构数据序列预测模型，主要思想是将灰数转化为实数构建预测模型，再还原为区间灰数。对于灰度波动较大的区间灰数序列，此类模型不仅对灰度变化较大的区间灰数拟合精度低，并且不能反映灰数灰度的未来的发展趋势。

对于区间灰数序列，本文将分析在核和“灰度不减”公理下构建的传统预测模型的误差情况。重新构造两组能够反映上、下界变化特征的核序列，分别构建DGM(1，1)模型；根据将两组预测值与传统预测模型结合；最后推导得到新的区间灰数预测模型，并用算例验证了模型的可行性。

1 基本概念

定义1[19]：既有下限a(k)又有上限b(k)的灰数称为区间

定义2[19]：区间灰数⊗(k)的取值范围称为测度或信息域，记做u(k)=b(k)-a(k)。

定 义 3[19]：存 在 区 间 灰 数 ⊗(k)∈[a(k)，b(k)],则 称灰数，记为为灰数⊗(k)的核；

公理1[19]：（灰度不减公理）两个灰度不同的灰数进行和、差、积、商运算时，运算结果的灰度不小于灰度较大的灰数，为计算方便，通常可将运算结果的灰度取为灰度较大的灰数的灰度。

推论1[19]：两个信息域不同的区间灰数进行和、差、积、商运算时,运算结果的信息域不小于信息域较大的区间灰数的信息域。

设存在区间灰数序列X(⊗)={⊗ (1)，⊗(2)，...，⊗(n)} ，其中 ⊗(k)∈[a(k)，b(k)]，根据定义1和定义2，由每个灰元的“核”和“测度”分别构成X(⊗)的核序列X0(⊗0)和测度序列UX，记作：

2 基于“灰度不减”公理的区间灰数预测模型

2.1 基于“灰度不减”公理的区间灰数预测模型建模原理

设 有 区 间 灰 数X(⊗)={⊗ (1)，⊗(2)，...，⊗(n)},⊗(k)其核序列和测度序列分别为：

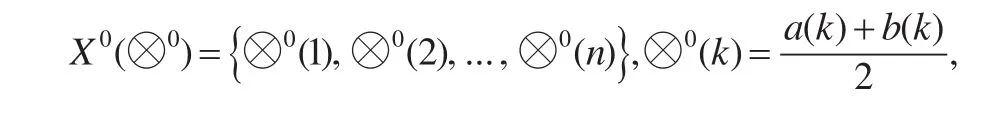
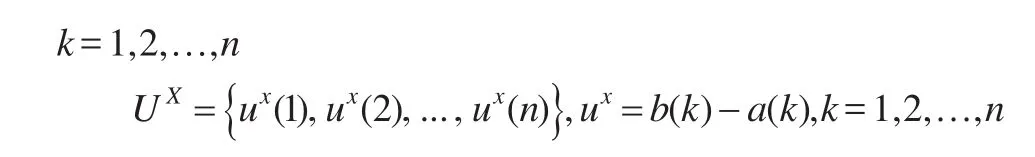
对核序列X0(⊗0)构建预测模型得到拟合序列

根据定义2和定义3，建立方程组：

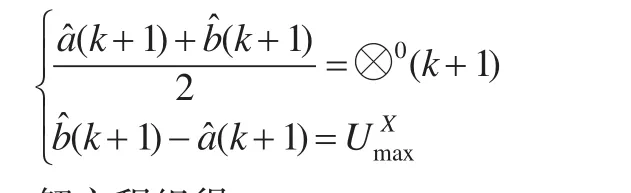
解方程组得：

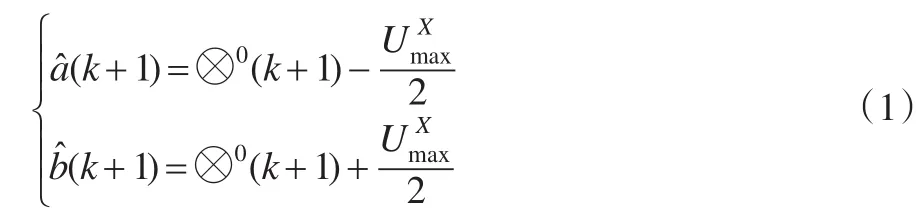
称（1）为区间灰数序列X(⊗)的传统预测模型。

2.2 传统预测模型误差分析

由公式（1）可知，序列X(⊗)的上、下限预测值分别为：

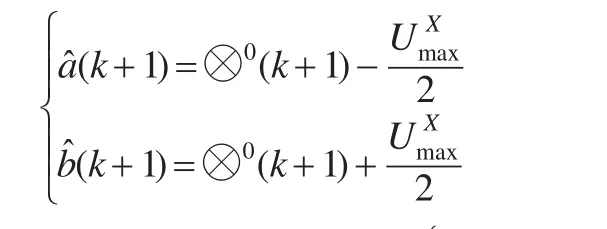
（1）当核预测值不存在误差时。假设⊗0(k+1)=⊗0即将模型误差都转移到测度预测误差上，则式（1）可调整为：

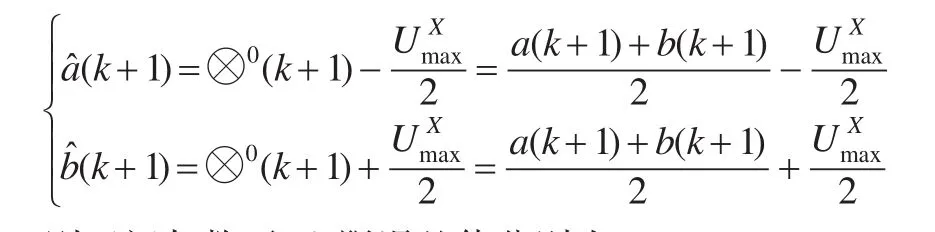
则区间灰数下、上限误差值分别为：

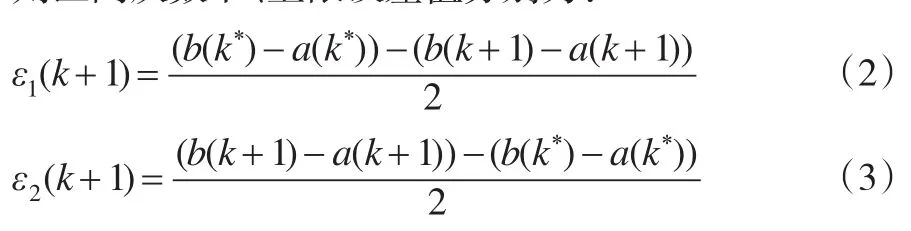
由公式（2）、公式（3）可知，当核预测值不存在误差时，区间灰数的上、下限误差值存在关系ε1(k+1)+ε2(k+1)=0，且ε1(k+1)≥0，ε2(k+1)≤0

（2）当测度预测值不存在误差时，假设预测误差都转移到核预测上，即其中即将测度预测值的误差都转移到核预测误差上，则式（1）可调整为：

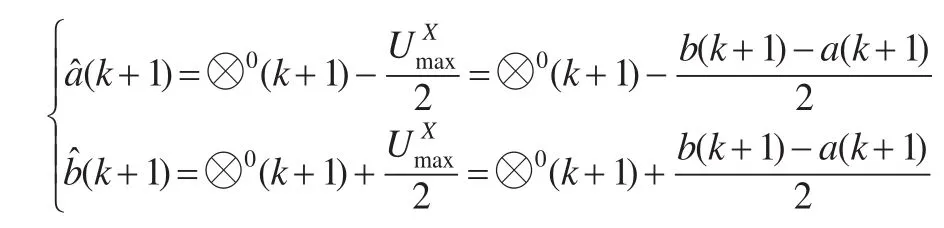
此时，区间灰数下、上限误差值相等，为：

综合公式（2）至公式（4）可得传统区间灰数预测模型的下、上限的误差分别为：

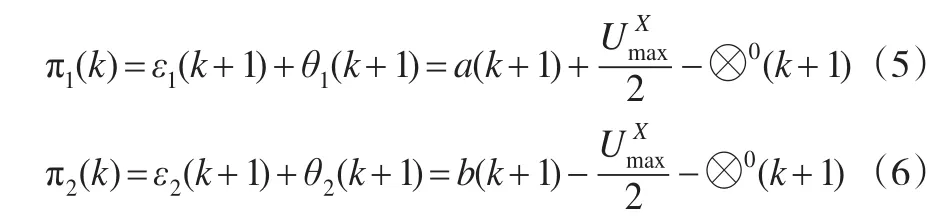
下、上限的平均误差为：

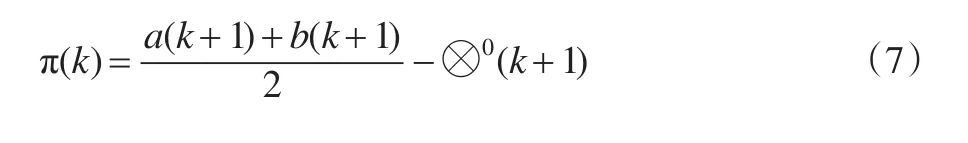
3 基于“灰度不减”公理改进的区间灰数预测模型

3.1 基于“灰度不减”公理改进的区间灰数预测模型构建

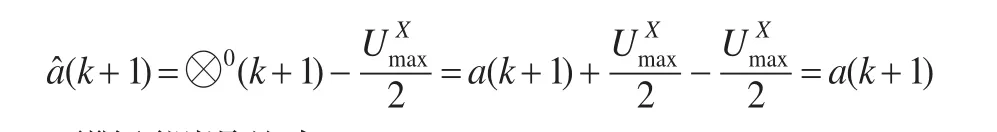
上限预测误差为ε2(k+1)=0

证毕。

由命题1可知对于传统区间灰数预测模型，当对上、限分别取核预测值分别为和时，区间灰数预测误差为0。当定义上、下限的核序列分别为时，可以提高模型预测精度。

为GM(1，1)模型的离散形式，简称DGM(1,1)模型；其中

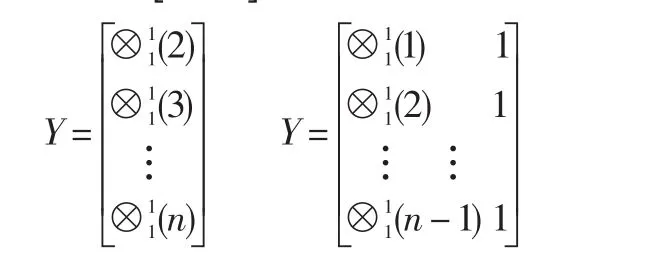
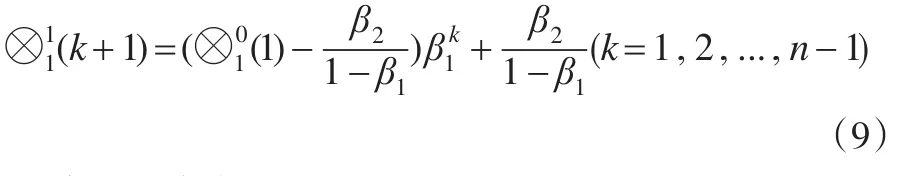
累减还原式为：

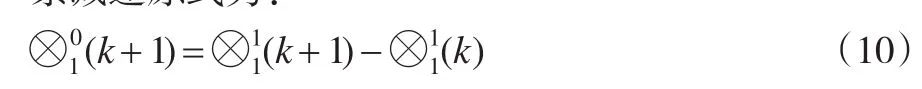
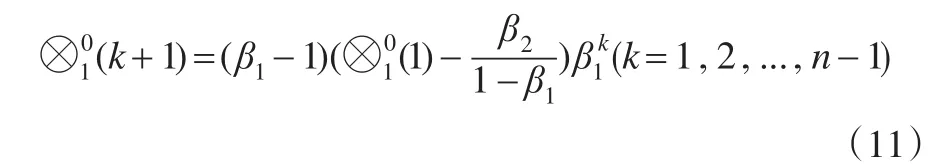
由式（9）和式（10）可得到序列

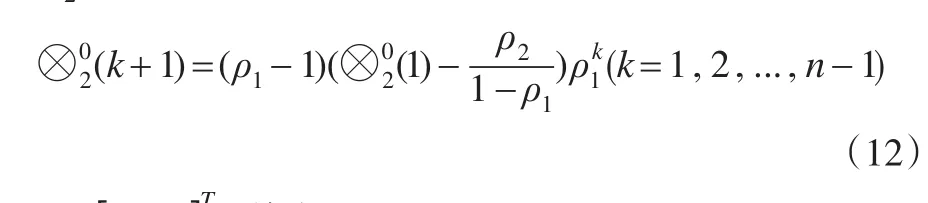
=[ρ，ρ]T，其中：

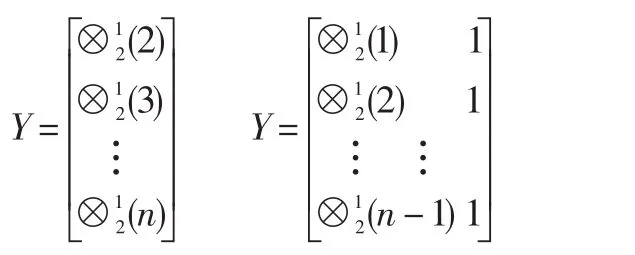
将上、下限核预测值分别带入公式（1）的上、下限预测模型，得到新的区间灰数预测模型为：

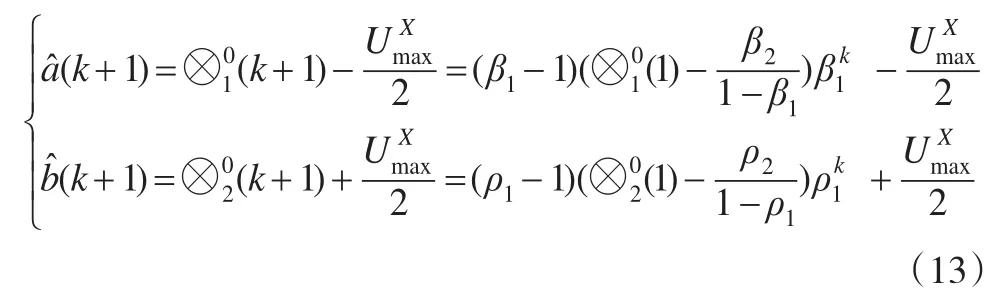
称式（13）为改进的区间灰数预测模型。

3.2 基于“灰度不减”公理改进的区间灰数预测模型建模步骤

基于传统区间灰数预测模型改进的区间灰数预测模型具体建模步骤为：

（1）由定义2得到序列X(⊗)的测度序列，得到最大测度值；

（2）由定义4分别确定序列X(⊗)的下、上限核序列；

（3）分别构建上、下限核序列的预测模型；

（4）将上、下限核序列的预测带入公式（1）。

3.3 基于“灰度不减”公理改进的区间灰数预测模型性质分析

（1）模型的适用范围

本文所研究的预测模型，通过对上、下限取不同的核序列，并分别建立DGM(1，1)模型，再结合“灰度不减公理”确定上、下限预测值。因此，模型的适用范围主要取决于DGM(1，1)模型的适用范围。

（2）模型预测值测度分析：

对于模型（13），其预测值的测度为：

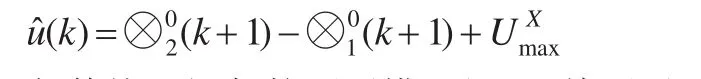
与传统区间灰数预测模型想比，其预测区间的测度随着区间灰数上下限的变化而变化，对于测度变化较大的区间灰数序列预测具有较好的适应性。

（3）预测值误差分析

4 算例分析

为了便于建模精度比较，将文献[20]的算例和建模方法与传统区间灰数建模方法及本文构建的区间灰数序列的预测模型的拟合结果进行比较，以验证新模型的有效性。

表1 X(⊗)中的区间灰数

根据本文建模过程构建表1中序列X(⊗)的预测模型，具体步骤如下：

（1）计算序列X(⊗)的测度最大值

由定义2得到区间灰数序列X(⊗)的测度序列为测度最大值为测队最小值为测度极值之差为显然区间灰数序列X(⊗)的测度变化较大。

（2）构造上、下限核序列

（3）构造上、下限核序列的预测模型

对上、下限核序列建立DGM(1，1)模型，可得：

（4）区间灰数预测模型构建

由式（13）可得：

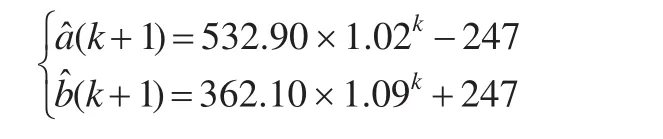
根据上式得到列X(⊗)的预测值，并与公式（1）的计算结果进行比较，如下页表2所示。

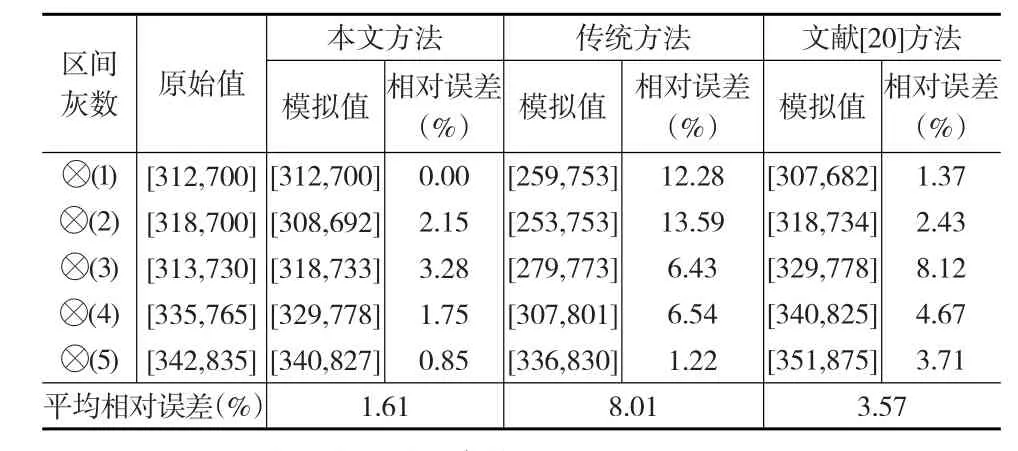
表2 模拟结果比较

由表2可知，本文构建模型的平均相对误差为1.61%，远小于传统方法，同时也小于文献[20]方法的平均相对误差，也就是本文模型有良好的预测精度。由表3对比三种方法得到的预测值的测度发现，公式（1）得到的测度预测值是保持不变的，而其他两种方法的测度具有时变性。综合考虑拟合值的预测误差和测度的时变性，本文方法具有较好的拟合和预测效果。

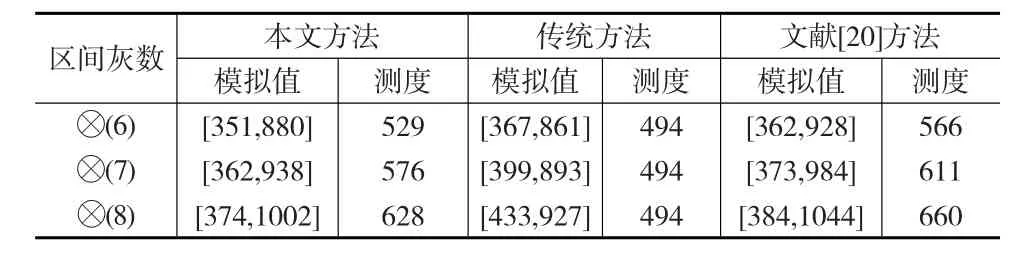
表3 预测值测度比较

5 结论

基于核和“灰度不减”公理构建的区间灰数预测模型，对于灰度或测度波动大的序列拟合效果不好，且无法预测序列测度的发展趋势。本文首先分析了传统区间灰数预测模型的上、下限预测值的误差组成，为提高区间灰数上下限的拟合精度，在原模型基础上，分别构造新的上、下限核序列；然后分别建立上、下限核序列预测模型；最后将上、下限核序列预测值带入传统预测模型中，推导得到新的预测模型。新的预测模型不仅遵循了“灰度不减”公理，同时通过对上、下限取不同的核预测值提高了模型的拟合精度。实现对测度波动较大序列的有效拟合，同时考虑序列的动态发展，使测度具有时变性，从而扩大了模型的应用范围。