高维数据中变量选择研究

宋瑞琪，朱永忠，王新军

（河海大学 理学院，南京 211100）

0 引言

如何从海量数据中提取有用的信息，是目前研究的热点以及难点。而在实际问题中，往往由于时间、地域、经费等因素的影响，使得人们寻找到的样本量低于研究问题的维度，这就出现了高维数据模型。

处理高维数据的关键在于变量的选择，按照其特征，变量选择可以分为子集选择法和系数压缩法。对于子集选择法，最早可以追溯到AIC准则的提出，并逐渐发展到BIC准则、向前回归、向后回归以及逐步回归等。刘立祥[1]通过逐步回归，选取影响水泥凝固放热的因素。子集选择法在变量选择的过程中容易受变量微小变动的影响，不具有较好的稳健性；同时子集选择法将变量选择与参数估计两步分开进行，增加了模型构建的误差，故子集选择法并不适用于高维数据分析。系数压缩法可以同时进行变量选择和参数估计，从而节省了模型构建的时间成本，克服了子集选择法的一些缺点。常见的系数压缩法主要有岭回归、Lasso、自适应Lasso、Elastic Net回归等。Groll等[2]基于生存模型，采用Lasso、岭回归以及Lasso和岭回归的组合模型，在仿真和实际应用中进行了方法的比较；Zou等[3]首次提出Elastic Net回归方法，并指出在实际问题中，Elastic Net回归往往优于Lasso估计；BALL等[4]将Elastic Net回归运用于生物科学研究中，基于Elastic Net回归方法选择合适的变量，从而通过最优氨基酸序列预测蛋白质结构。

本文对岭回归、Lasso、自适应Lasso以及Elastic Net回归的基本原理及实现进行了梳理，基于蒙特卡洛模拟实现变量选择。本文通过引进敏感性与特异性，来分析比较不同方法的适用领域，并将方法扩展到高维数据空间，拓展模型的应用。

1 模型简介

首先考虑最简单的一般线性回归模型：设x1，x2…xp为模型的p个自变量，y为解释变量，则自变量与解释变量之间可以建立如下线性回归模型

其中β0是截距项表示模型的回归系数，ε为随机误差项，并且满足假设(xi1，xi2…xip;yi)，(i=1，2…n)是n组观测变量，X为n×p阶设计矩阵，并且假设变量已经进行了中心化处理，则式（1）的最小二乘估计可以表示为：

最小二乘估计是常用的一种系数估计方式，在满足线性回归的一般假设条件下，最小二乘估计的估计结果具有无偏性。但是最小二乘估计又存在局限性，当自变量之间存在多重共线性问题时，回归系数的估计具有很大的不稳定性。

岭回归：为了解决最小二乘估计的缺陷，Hoerl和Kennard于1970年提出了一种新的系数估计方法——岭回归。通过在式（2）中加入惩罚项，从而控制了回归系数的膨胀性。岭回归的定义如下：

其中，λ≥0是调节参数，并称为L2惩罚项。调节参数λ控制着RSS和L2对模型中回归系数β估计的相对影响程度，适当的λ值可以使β1，β2…βp中一些系数往0的方向收缩，当λ=0时，岭回归为一般的线性回归模型。与最小二乘估计不同的是，岭回归以增大模型的偏差作为代价，通过压缩模型的系数来减少模型的预测方差。但是岭回归也存在一定的缺点，其并不会将任何一个变量压缩为0（除非λ→∞），即岭回归并没有实现真正意义上的变量选择，当自变量的个数p很大时，模型中将会含有大量的解释变量，不利于模型的解释。

Lasso回归：1996年Tibesirani将式（3）中的L2惩罚项改为了L1惩罚项，并将得到的新的回归模型定义为Lasso回归模型：

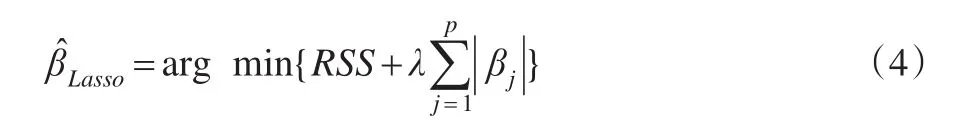
与岭回归类似，Lasso回归的第一项RSS表示损失函数，度量了回归模型拟合的好坏，第二项λL1为惩罚函数，可以将回归系数中一些很小的系数压缩为0，实现了回归模型中稀疏模型的构建，从而克服了岭回归中不能将回归系数压缩为0的缺点。

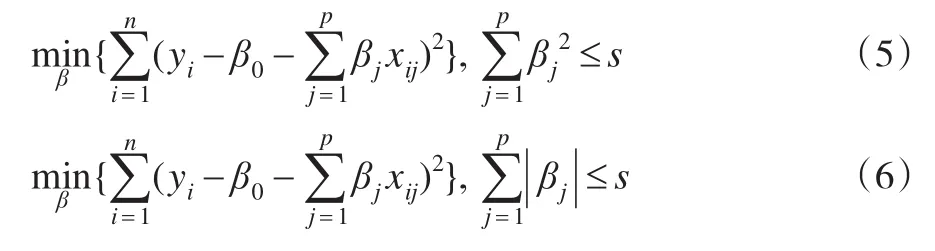
考虑Lasso的等价形式（6）：在条件量选择。式（5）是岭回归的等价形式，它表示在的限制下，使得RSS尽量的小。

自适应Lasso（简称aLasso）：aLasso是对Lasso模型的改进，它将回归系数赋予不同的权值，并对惩罚函数进行了二次惩罚，其主要思想是：将贡献度较大的回归系数进行较小程度的惩罚，而将贡献度较小的回归系数进行较大的惩罚。其回归模型如下所示：

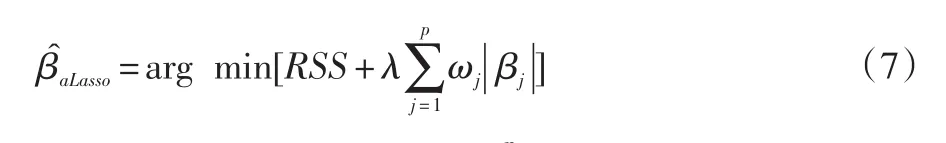
其中ωj≥0 为惩罚权重表示改进后的惩罚函数。ωj的选择是模型中变量选择好坏的关键，当ω=1时，为一般意义的Lasso模型。取作为自适应 Lasso的惩罚权重，其中表示 Lasso估计中的回归系数，本文取γ=1。式（7）可以表示为：

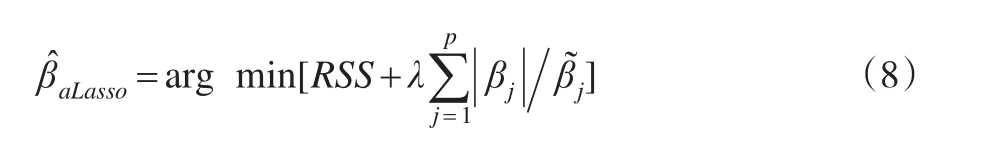
值得强调的是，式（7）与式（8）是一个凸规划问题，并不会受局部极小点的影响，并且其全局极小点也很容易获得。

Elastic Net回归：Lasso虽然具有良好的性质，可以选择稀疏模型，但是当两个或以上变量具有很强的相关性时，Lasso会随机选取其中一个变量而排除其他变量。从模型的稀疏性角度来看，Lasso模型无疑是满足要求的。但是从实际生产的解释角度而言，人们更希望将所有的相关变量都选入模型中。基于以上考虑，2005年，Zou和Hastie将岭回归模型和Lasso模型相结合，提出了Elastic Net回归模型：

产科实验指标结果均进行统计学计算,使用统计学软件SPSS18.0。自然分娩率、新生儿窒息率等计数指标结果均以%形式展开,进行卡方检验。P<0.05,说明观察指标结果差异有统计学意义。

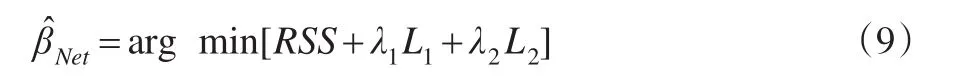
其中λ1和λ2是模型中两个非负的惩罚参数。由式（9）可以看出，当λ1=0时，Elastic Net回归模型便是岭回归模型，当λ2=0时，此时的Elastic Net回归模型为Lasso回归模型。令则式（9）可以表示为：

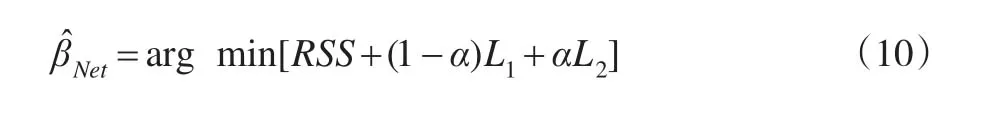
2 随机模拟

2.1 低维数据

假设变量服从一般线性回归模型y=Xβ+σε，其中

模型1：设回归系数的真实值为β=(3.7，1，0，2，0，0)，变量的影响程度介于较大影响程度和较小影响程度之间。取σ=3，表示信噪比（SNR）为5.7，用ρ|i-j|表示任意两个解释变量Xi与Xj之间的相关系数，并且取ρ=0.5表示中等相关。取样本量n=50，重复进行100次试验。基于岭回归、Lasso、自适应Lasso以及Elastic Net回归，分别预测模型的回归系数并将预测结果绘制在图1中。由图1（见下页）可以看出，所有模型都可以正确识别3个重要变量。针对变量X3，X5与X6（对模型没有影响），Lasso、自适应Lasso和Elastic Net回归三种回归均将系数压缩为0，但是自适应Lasso具有较小的预测误差，在图中表现为箱线图的箱线较短，再其次是Lasso估计。而对于变量X1，X2与X4（对模型表现出不同程度的影响），岭回归、Lasso以及Elastic Net回归的预测结果是有偏的，在图中表现为箱线图的中心位置偏离真实值。对于变量X2的预测，Elastic Net回归很好地将回归系数压缩为0，自适应回归将X4的系数压缩为0。综上比较，无论是预测对模型有影响的回归系数，还是预测对模型没有影响的回归系数，自适应Lasso都表现出了很好的预测效果。

客观上，可以用敏感性（Sensitivity）和特异性（Specificity）两个指标来评价回归模型中参数选择的好坏，敏感性和特异性的定义如下：

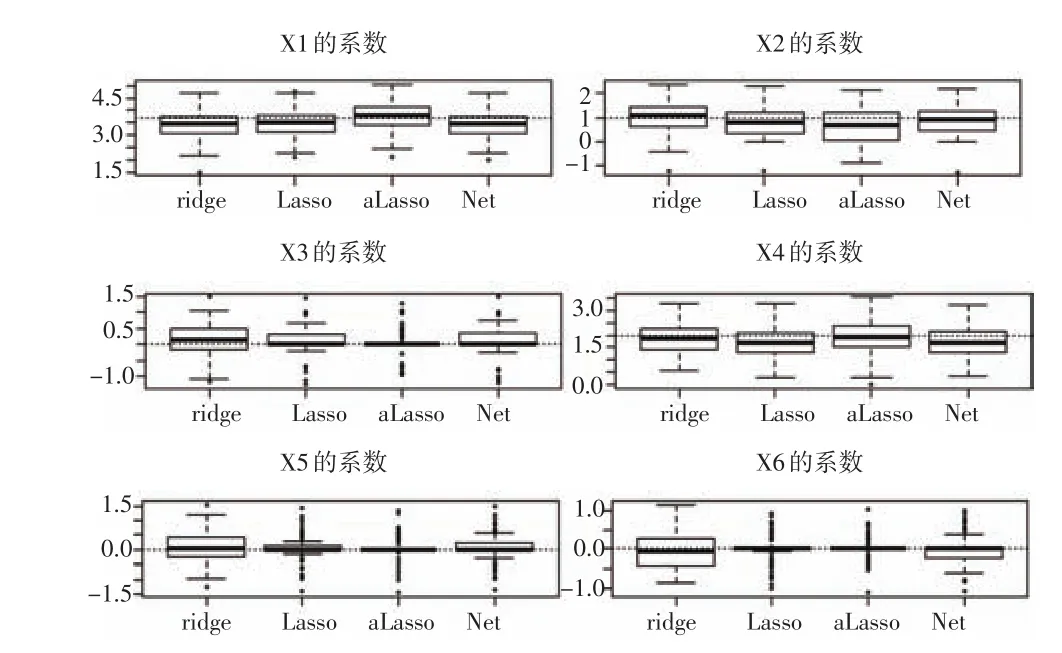
图1 回归系数估计结果

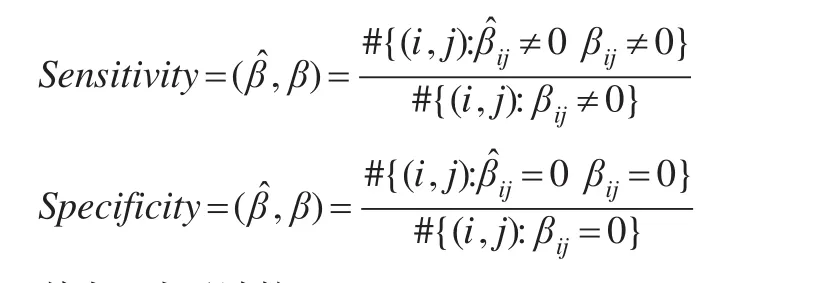
其中#表示计数，Sensitivity∈[0，1]，Specificity∈[0，1]，值越接近1，变量选择的效果越好。与模型1相同，取样本量n=50，100，150，分别重复进行100次试验，计算每个样本量下模型的敏感性和特异性，结果见表1。岭回归只是对模型的系数进行了压缩，并没有真正的实现变量选择，因此在岭回归估计中，其敏感性为1，特异性为0，这与岭回归的性质相一致。对于Lasso、自适应Lasso以及Elastic Net回归，当样本量增大时，敏感性和特异性也会随之增大，说明模型的选择效果也在变好。而在相同样本量的条件下，比较四种模型的敏感性和特异性，发现自适应Lasso对于变量选择的能力会优于其他三种模型。

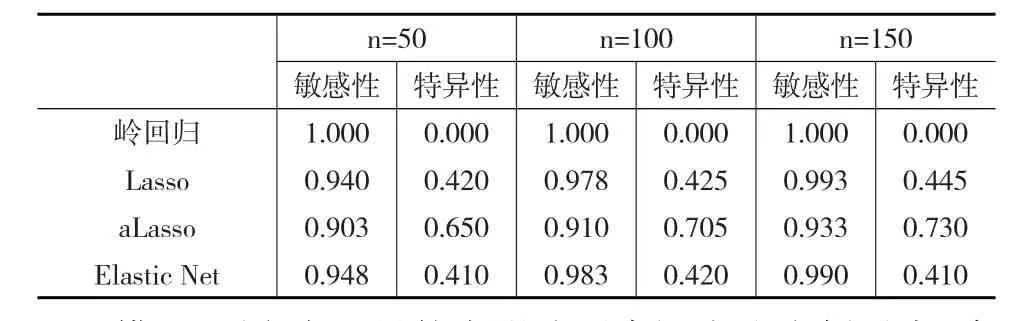
表1 不同样本量下模型的敏感性与特异性

模型2（含有少量较大影响因素）：在这个例子中，令β=(4，1.5，0，0，2，0，0)，Xi与Xj之间的相关性为ρ=0.5，xj1与xj2之间的相关系数为cor(j1，j2)=(0.5)|j1-j2|。 取σ=1，3，6，其对应的SNR分别为21.25，2.35和0.59，取样本量n为50和100。

对于模型2和模型3，针对每一个组合(n，σ)（n=30，50，σ=1，3，6），本文均进行100次模拟试验，计算每次试验RPE。选取每个组合中RPE的中位数作为最终模型的RPE。

表2显示了仿真数据的结果，从表2中可以得到如下结论：第一，当样本量增大时，模型的精度越来越好；第二，针对模型2，自适应Lasso似乎自动结合了岭回归和Lasso的优点，在低等或中等水平下的信噪比下，自适应Lasso的预测精度高于岭回归和Elastic Net回归，在高等水平的信噪比下，自适应Lasso的预测精度显著高于Lasso；而对于模型3，岭回归的预测精度明显高于其他模型，其次是Elastic Net回归，这与模型的定义保持一致。对于含有大量较小影响因素的模型，Lasso、自适应Lasso将不显著的影响变量的系数压缩为0。Elastic Net回归是Lasso与岭回归的组合模型，既有Lasso的特点，也保留了岭回归的性质。

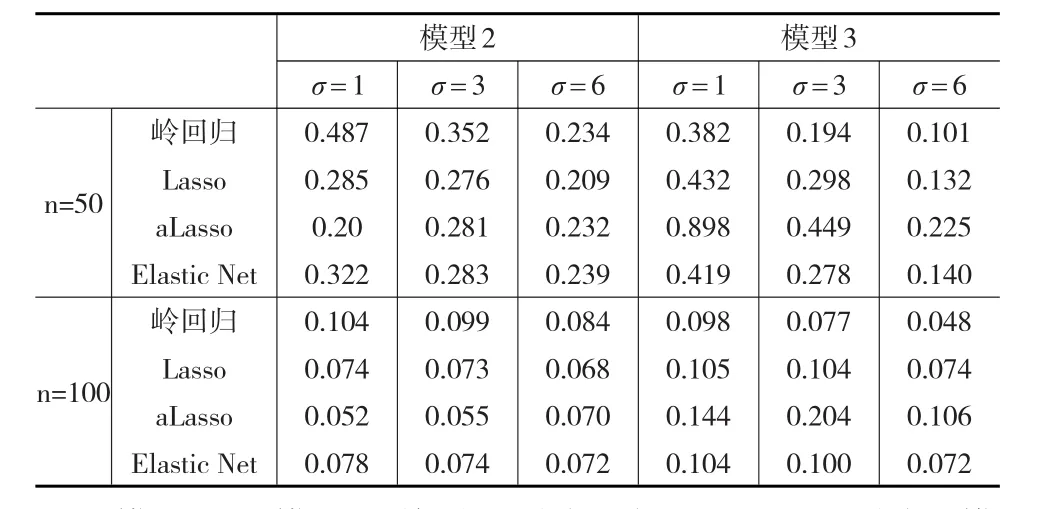
表2 比较各模型的RPE值

模型2和模型3说明，不同的方法适用于不同的模型。一般情况下，只有一小部分解释变量与响应变量不相关或相关程度很小时，自适应Lasso展现了其独特的优势，而当每个解释变量的解释程度大致相等时，本文应该选用岭回归模型。

2.2 高维数据

当自变量的个数大于样本量的个数（即p＞n）时，为高维数据，上文已经讨论了典型的变量选择问题，在这种情况下，固定预测变量的个数，不断增大样本量的个数，从而减少预测误差，即上文中讨论的是p＜n的情形。而在实际问题中，经常出现p=pn→∞的例子，如基因问题，通过确定急性白血病的基因组合，消除没有影响或影响较小的基因，寻找致病因子，从而寻找并制定合适的医疗方案，促进医学的发展。虽然p很大，但是由于时间、经费、抽样技术、地理跨度以及不可避免的客观因素如基因排序等因素的影响，往往不能满足p＜n，这就是接下来将要讨论的高维数据问题。

同样假设变量服从一般线性回归模型y=Xβ+σε，其中取σ=3，用ρ|i-j|表示任意两个解释变量Xi与Xj之间的相关系数，分别取ρ=0.5和ρ=0.85，表示变量之间中等相关和高等相关。取自变量p=70，重复进行100次试验。考虑如下两种情形：

（1）样本量n=70，回归系数即只有20个变量与解释变量有关，此时p=n。

（2）样本量n=30，回归系数的设定与第一种情况保持一致，此时p＞n。

利用蒙特卡洛随机模拟，对于每一个(ρ，n)组合，分别计算以上两种情形下模型的敏感性、特异性以及RPE，结果见表3。可以发现：（1）在相同样本量的条件下，比较四种模型的敏感性和特异性，发现Elastic Net回归对于变量选择的能力会优于其他三种模型，增大样本量，敏感性与特异性也会增大。（2）固定自变量的个数p值和相关系数ρ值，当增大样本量时，模型的相对预测误差（RPE）也会减小，说明增大样本量可以减少模型的预测误差。而往往在现实生活中，很难获得如此多的样本量。此时应该选择合适的解释变量加入模型，盲目增加模型的维度反而不利于模型的构建，只有加入与因变量真正相关的自变量，才会降低模型的预测误差。（3）对于正确变量的选择比例，Elastic Net回归所占比例最高，其次是Lasso和自适应Lasso，岭回归的选择效果最差。（4）比较模型的预测误差，Elastic Net回归的RPE值最小，其次是Lasso。岭回归在模型预测的过程中并没有实现真正的变量选择，对于0值得预测，反而出现了不一致性。当相关系数值增大时，岭回归、Lasso、自适应Lasso的RPE值都有所增大，Elastic Net回归反而有所减少。在高维数据中经常会出现共线性问题，即使变量之间是相互独立的，由于维数很高，样本的相关性也可能会很高。高度相关的变量中，L1惩罚会表现得很不好，共线性问题会严重降低Lasso的预测能力。当相关性很高的时候，Lasso的预测路径很不稳定。自适应Lasso继承了Lasso估计的不稳定性。而当变量之间的相关性很高的时候，Elastic Net回归可以很好地提高预测精度。

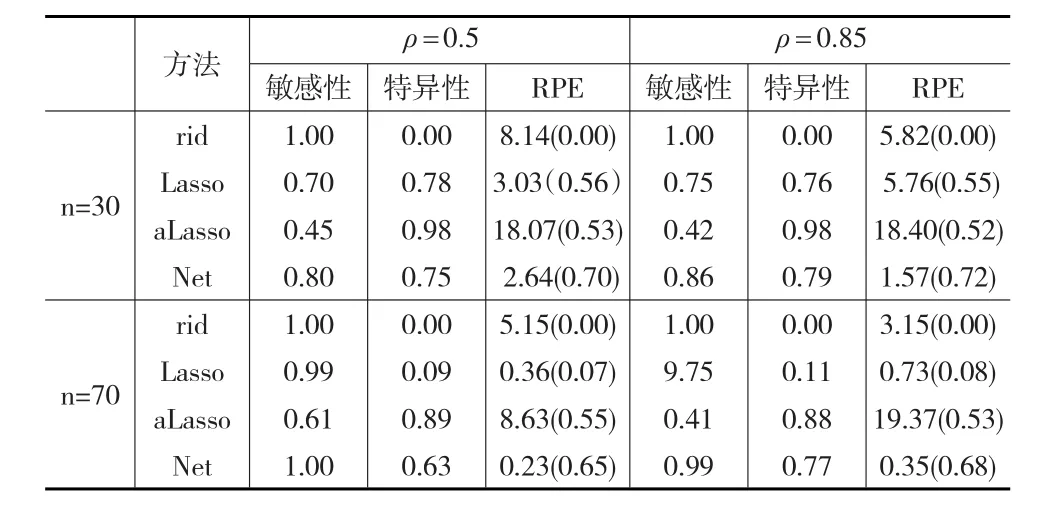
表3 高维数据下各方法的比较

3 结论

通过随机模拟表明：第一，在低维模型中，当其他条件一致时，比较四种模型的敏感性和特异性，发现自适应Lasso对于变量选择的能力会优于其他三种模型。需要强调的是，本文并未表明某种模型具有绝对优势，而是为了说明不同模型适用于不同的数据类型，当只有小部分解释变量与响应变量不相关或相关程度很小时，自适应Lasso展现了其独特的优势，而当每个解释变量的解释程度大致相等时，应该选用岭回归模型。这一点在模型2和模型3中给出了解释；第二，在高维数据中，通过蒙特卡洛模拟实验数据，在相同样本量的条件下，比较四种模型的敏感性和特异性，发现Elastic Net回归对于变量选择的能力会优于其他三种模型。而增大模型的相关系数时，岭回归、Lasso、自适应Lasso的RPE值都有所增大，Elastic Net回归反而有所减少。当变量之间的相关性很高的时候，Elastic Net回归可以很好地提高预测精度。