因变量数据波动对直线回归和相关的影响

丁 勇

（南京医科大学康达学院 理学部，江苏 连云港 222000）

0 引言

回归和相关是统计学研究的重要内容，也是在实际问题中得到广泛应用的统计方法[1-4]。原始数据的获得，由于各种原因，或多或少的带有一些误差，这些误差会导致数据的波动，从而对计算结果产生一定的干扰，当数据量庞大、计算过程较复杂时，这些干扰会相互影响、传播到下一步。因此，分析数据波动对结果的影响，寻找更稳健的算法，减少数据波动带来的干扰，使结果更客观准确、分析更可靠，是一个值得研究的课题[5]，特别是在大数据时代的今天。经典的最小二乘法、最小一乘法以及各种加权法，本质上就是从不同的角度出发，探讨如何尽可能地减少数据波动的影响[6-9]。本文就最常用的直线回归和相关问题探讨因变量数据波动的影响，发现其中的规律性。

1 定理、性质和几何意义

设 有 一 组 观 察 数 据x=(x1，x2，…，xn)、y=(y1，y2，…，yn)，将x作为自变量，y作为因变量，拟合直线回归方程y=a+bx，则由最小二乘法可得[8,9]:斜率截距a=yˉ-bxˉ以 及 相 关 系 数其 中为自变量的离均差平方和为因变量的离均差平方和，为离均差积和。

在统计学中，回归和相关是紧密联系的两个部分。当因变量的数据有波动时，因变量的值会随之改变，下面讨论yj的改变对回归直线和相关的影响。

函数在某一点的导数描述了这个函数在这一点附近的变化率，因此，可用求导数的方法，探讨某个因变量yj的数据波动对斜率、截距和相关系数的影响。对相关问题，本文更关心的是两个变量之间的相关程度|r|，但由于对绝对值求导数不方便，故而考虑r2，因为当r的绝对值变大（小）时，r2也变大（小）。当lxy=0时，b=0，r=0，此时直线和相关都没有什么意义，所以不考虑lxy=0的情况。

所以：

引理1[10]：Cauchy不等式:为任意实数(i=1，2，…，n)，等号当且仅当ai与bi对应成比例时成立。

从而，当xj≠xˉ时：

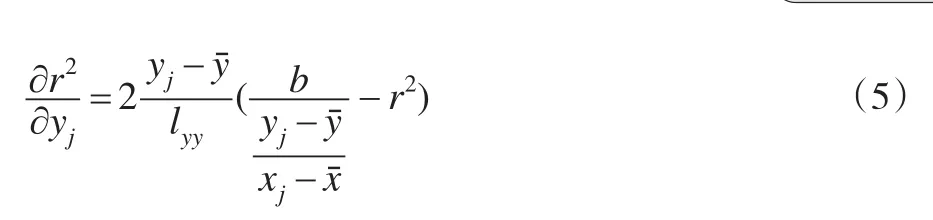
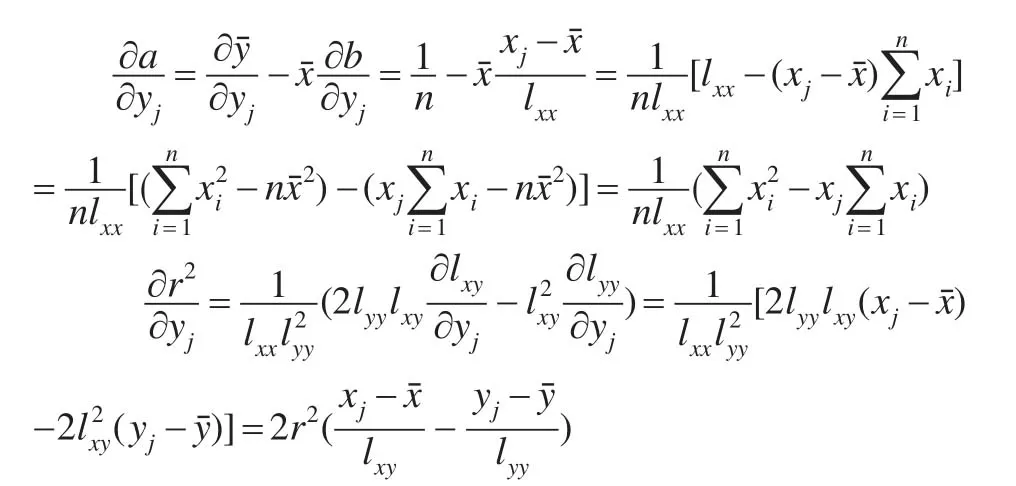
由定理1可得如下3个性质。

性质1：当xj＜xˉ时，b随着yj的增大（减小）而减小（增大）；当xj=xˉ时，b不受yj的大小影响；当xj＞xˉ时，b随着yj的增大（减小）而增大（减小）。

数理统计已证明[8，9]，回归直线经过点 (xˉ，yˉ)。

由公式（1）可得性质1，性质1的几何意义为：在自变量样本均数xˉ这一点，函数值波动对斜率没有影响，从来看，也是显然的，当时与yj无关；该点的函数值增加（减少）时，回归直线平行地上（下）移。在其左边的点，函数值的增大（减小）将使斜率变小（大）；在其右边的点，函数值的增大（减小）将使斜率变大（小）。

性质2：当xˉ=0时，a随着yj(j=1，2， …，n)的增大（减少）而增大（减少）；当时，a不受yj的大小影响；如果xˉ＜0 ，则当时，a随着yj的增大（减小）而增大（减小）；当时，a随着yj的增大（减小）而减小（增大）；如果xˉ＞0，则当时，a随着yj的增大（减小）而减小（增大）；当时，a随着yj的增大（减小）而增大（减小）。

由公式（3）可得性质3。当xj≠xˉ时，由公式（4）、公式（5）可得性质3的几何解释：将经过两点 (xˉ，yˉ)、(xj，yj)的直线斜率与确定值进行比较，或者将回归直线的斜率b与斜率的比值，与相关系数的平方r进行比较，可以判断相关系数如何受函数值的影响。例如，当时，在左边的函数值增大（减少）将使相关系数的绝对值减小（增大）。

定理2：

由r与b的计算公式可知，r、b都与lxy同号，所以不等式（6）和式（7）几何意义说明，以下4种情况的因变量的数据波动，在不超过回归直线的情况下,可以提高数据的相关性:

①正相关（lxy＞0），在xˉ左边、回归直线上面的点向下移动；

②正相关（lxy＞0），在xˉ右边、回归直线下面的点向上移动；

③负相关（lxy＜0），在xˉ左边、回归直线下面的点向上移动；

④负相关（lxy＜0），在xˉ右边、回归直线上面的点向下移动。

特别若r2≈1时，如果yj＜a+bxj，则：

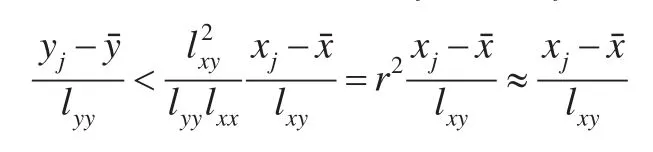
类似可知，如果yj＞a+bxj，则

由公式（3）可知，当相关系数较大时，在回归直线下面的点向上移动或回归直线上面的点向下移动（不超过回归直线），都可以提高变量的相关性。

2 实例分析

2.1 数据构造

为验证性质1至性质3，本文构造自变量包含xˉ和数据。在引理中，取ai=xi，bi=1，可知这两个数的大小关系为：如果xˉ＜0 ，则如果0 ，则

记x=(x1，x2，…，xn-2，xn-1，xn)，不妨设x1，x2，…，xn-2（n＞2）已知，令xn-1=xˉ，则有：

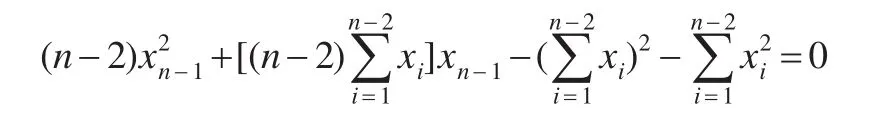
解一元二次方程得：

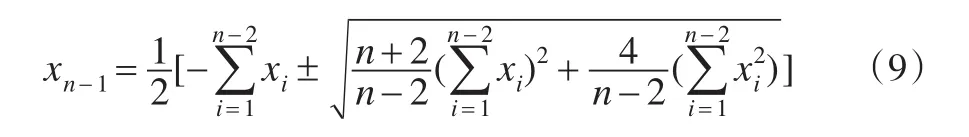
将得到的xn-1代入式（8）可得相应的xn。

取x1，x2，x3，x4为一组正数1，4，7，10，为使x5，x6也为正数，式（9）的开方取正号（取负号也行，可以得到另外一组数据）。按公式（8）和公式（9），得到表1的一组x数据（数据重新按从小到大排序），再取一组y数据（见表1），由这批数据可求出：xˉ=5.8375,yˉ=22.1667,lxx=47.2776,7.1873,r=0.9733，b=3.5891，a=1.2152。

表1 数据计算

2.2 结果分析

表1的散点图和回归直线如图1所示，已知回归直线经过中心点（xˉ，yˉ)（图1中“○”），当某个yj有微小的波动时，近似认为对yˉ没有影响。对于xj＜xˉ的情况，如果yj变大，可以看成回归直线围绕中心点在左边向上升，从而直线的斜率变小；如果yj变小，此时回归直线围绕中心点在左边向下降，从而直线的斜率变大；对xj＞xˉ有类似的结果，这与性质1是相符的。

图1 直线回归图

一般的直观感觉认为，当数据点向回归直线靠近时，变量的相关性会提高（相关系数绝对值增大），但事实并非完全如此。定理2证明了4种情况下这个结论是正确的，而另外4种情况（正相关、在左边、回归直线下面的点向上移动，正相关、在xˉ右边、回归直线上面的点向下移动，负相关、在xˉ左边、回归直线上面的点向下移动，负相关、在xˉ右边、回归直线下面的点向上移动）则不一定，下面通过一个例子进行说明。

取x如表1所示，y=[0 1.1 0.5 1.6 0.6 1.7]（图2中“*”，回归直线为虚线），此时相关系数r=0.7526，由图2可知，y1=0（图2中“*”）在回归直线（图2中虚线）下面，将y1向上移动，变为0.1(图2中“○”)，此时相关系数r=0.7350（此时的回归直线见图2实线），相关性反而变差了。

图2 数据点移动对相关系数的影响

3 讨论

直线相关与回归是统计的基础内容，其研究成果也很成熟。本文从因变量数据波动入手，深入探讨了数据波动对直线相关和回归影响的问题，挖掘出一些有价值的新信息。从公式（1）至公式（3）得到相应的3个重要指标：自变量均值xˉ、自变量的二阶原点矩与一阶原点矩的比值因变量离均差平方和与离差平方和的比值这3个指标分别对应斜率、截距和相关系数：前2个指标值可看成阈值，通过自变量与其比较大小来判断因变量波动对回归影响，在这2个点，因变量波动不影响回归直线的斜率、截距；后一个指标，要通过某个点与平均值的点的斜率与该指标比较大小来判断该点因变量波动对相关的影响，例如，当时，因变量波动不影响相关系数。另一个有趣的现象是：两个斜率（回归直线的斜率与某个点与平均值点的斜率）之比与相关系数平方（r2）的大小的比较，也有同样的效果。

3个公式的偏导数大小也是判断数据波动影响大小的依据，从导数的数学意义可知，其绝对值越大，数据波动产生的影响也越大，表1的实例数据也充分说明了这一点。

本文还纠正了一般的直观感觉：认为当数据点向回归直线靠近时，变量的相关性会提高，这样的情况仅在一定的条件是正确的，本文给出了这样的条件以及不满足这样条件的一个反例。

通过以上分析，使我们对因变量数据波动对直线回归和相关的影响有了更深入的认识。