网络数据环境下动态抽样框的构建及其应用
朱 钰,王 恬
(西安财经大学a.统计学院;b.西安统计研究院,西安 710061)
0 引言
20世纪80年代由美国人提出“大数据”一词,随着信息技术和互联网的不断发展,“大数据”逐渐融入人们的日常生活、学习与工作。大数据的出现,无疑是给传统的统计工作带来了巨大的挑战。2009年维克托·迈尔·舍恩伯格及肯尼斯·库克耶在《大数据时代》一书中提出采用所有数据的方法(取代抽样调查)。随后,许多国内学者也纷纷在各大期刊上发表文章,并指出“大数据时代不需要抽样”的观点。而这种观点无疑是将抽样技术与大数据分割为独立的个体来讨论,是一种片面的理论认识。大数据理论是指尽最大可能收集与研究对象相关的“数据”(包括文档、视频、图片等非结构化数据),通过数据处理技术进行分析,找寻研究对象与研究目的之间的关系,用以发现和解决问题的一种理论。《大数据时代》提出了三个最显著的变化:一是样本等于总体;二是不再追求精确性;三是相关分析比因果分析更重要。针对第一个显著变化“样本=总体”,给传统的统计抽样技术带来巨大的挑战——抽样框确定,网络数据满足上述的“5V”特性,面对瞬时万变、复杂多样的数据环境,如何针对所要研究的问题,确定抽样调查中的抽样总体?如何将传统的抽样框变化为适应大数据时代下的抽样框?这都是需要进一步研究和探索的问题。
本文将针对大数据给抽样技术带来的第一个挑战——抽样框变动问题进行深入地研究,从源头上构建大数据背景下抽样技术实施的基础条件,为以后改进抽样方法提供捷径。
1 理论基础
1.1 大数据的定义
在构建网络数据环境下的动态抽样框之前,先将文中提出的网络数据环境所涉及的背景——大数据进行简单的定义。
目前对大数据的定义还没有形成统一的意见。麦肯锡全球研究院将大数据定义为:无法在一定时间内使用传统数据库软件工具对其内容进行获取、管理和处理的数据集合;维基百科将大数据定义为:所涉及的数据量规模巨大到无法通过人工,在合理时间内达到截取、管理、处理、并整理成为人类所能解读的信息。针对不同专家对大数据的定义,根据统计学理论,本文对大数据的定义如下:
定义1:大数据(Big Data)是指所研究问题针对资料收集规模巨大、数据资料复杂等问题,无法通过传统使用的工具、软件在尽可能短的时间内实现数据的分类、处理、分析与存储,需要用新的处理模式和流程优化能力来分析信息的集合。
网络数据环境下动态抽样框构建的主要核心是:动态抽样框构建的理论支撑,由于目前这方面的研究甚少,所以本文就从抽样的基本原理入手,结合网络数据背景的特点,再融入抽样框构建的关键来构建动态抽样框。
1.2 抽样原理
采样过程所应遵循的规律,又称取样定理、抽样定理。采样定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据。本文将在采样定理深入理解的基础上对抽样技术中的抽样原理进行定义,下面将从大数据背景下的动态抽样框构建入手,对抽样原理给出统计学方面的定义:
定义2:设所需要调查对象的目标总体是N,抽样总体为M,调查总体为S;且对任意研究对象满足如下条件:

利用一定的统计抽样方法对满足抽样原则的对象进行筛选,最终达到利用调查总体S来估计抽样总体M,并在此基础上利用统计推断理论来得到研究对象总体N的相关信息的方法称之为抽样原理。
上述三者总体之间的关系可由图1表示:

图1 N、M、S三者关系反映图
在研究抽样框之前,有必要对目标总体与抽样总体之间的关系进一步说明:理想的状态是抽样总体应该与目标总体完全一致,也就是所有目标总体单元和抽样总体单元完全是一一对应的关系。但在实践中,两者不一致的情况却时有发生。就如图1所展示的那样,会存在未覆盖的地方。同时,在调查中也会出现无应答的部分,使得调查总体与抽样总体也不能一一对应。
定义3:(抽样框)设由目标总体单元x1,x2,...,xN构成的目标总体为N,且抽样单元s1,s2,...,sM构成抽样总体是M(M⊆N),当满足下面三个条件时称抽样总体M为抽样框。
①目标总体单元xi(i=1,2,...,N)可以包含一个个体,也可以包含若干个个体;
②抽样单元sj(j=1,2,...,M)可以包含一个个体,也可以包含若干个个体;
③sj⊆xi(i=j)
也就是说,抽样框是抽样总体的具体表现。通常,抽样框M是一份含所有抽样单元的名单,给每个抽样单元编上号码,就可以按照一定的随机化程序进行抽样;抽样单元sj是构成抽样框的基本要素(抽样单元还可以分级)。一般意义上,好的抽样框不仅与目标总体保持一致,而且还尽可能多的提供与研究的目标量有关的辅助信息,以便调查人员利用这些辅助信息搞好抽样设计,提高抽样估计效率。
抽样框的设定与选择不同对总体的估计也不同,也会出现抽样框误差,具体表现在:定义3中M∈N时、总体中单元数N不准确;上述两种情况都会导致利用样本统计量对总体参数进行估计就可能产生偏倚(误差)。
1.3 相关理论
(1)大数定理:
设X1,X2,...,Xn是相互独立且服从同一分布的随机变量序列,对任意的i(i=1,2,...,n)有数学期望E(Xi)=μ;令随机变量序列的任意n个单元的算术平均数为:
则对任意的ε>0,有:
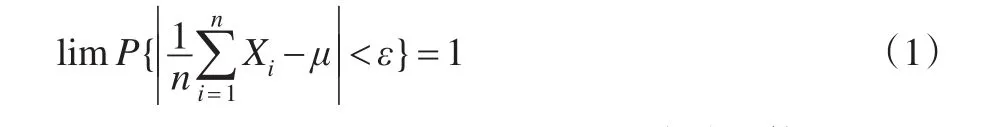
也就进一步说明抽样过程中的样本代替总体的原理,同时,大数定理说明了随机事件的稳定性。特别地,当n→∞时,算术平均值与数学期望值μ就会越接近。即样本量越大,其统计特性就会越接近总体的分布特征。
(2)极限定理:
设X1,X2,...,Xn是相互独立且服从同一分布的随机变量序列,对任意的i(i=1,2,...,n)有数学期望E(Xi)=μ、方差D(Xi)=σ2;令n个随机变量之和为则有式(2)成立:
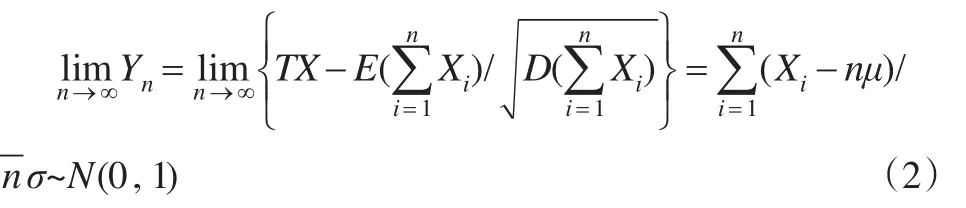
从式(2)表明,无论随机变量序列服从什么分布,从中抽取n个样本进行研究时,只要n足够大,其样本平均数就近似的服从数学期望为μ、方差为的正态分布,即明显地,当n→∞ 时,抽样误差会越来越小,所以通过合理的抽样方法一定可以获得总体N的特征。
2 构建动态抽样框的方法
传统情况下抽样框的建立方法与思路在上文已做了说明,但是,在大数据背景下,构建抽样框的初始条件(总体N确定)难以满足,这就对抽样技术的研究提出了挑战;且在大数据背景下不同时间段、相同时间段内满足条件的进入总体的数据流是不定的(流速未定)。所以,下面将针对上述问题进行大数据背景下动态抽样框的构建问题进一步加以说明:
2.1 动态抽样框的定义
定义4:单位时间t=1s内数据流速为V(t)且t是一个服从一定条件的随机变量,则在任意时间段Δti=tj-ti(j>i)内的总体Nij满足:

也就可以通过式(3)来定义动态抽样框的总体Nij。显然,Nij是一个时间ti,tj及流速V(t)代表单位时间流入的数据的个数,是不断变化的量,即Nij就是时间ti→tj的数据总量,即抽样框;随着i,j的变化形成的动态总体,即动态抽样框。动态抽样框的构建过程可以用图2加以说明:
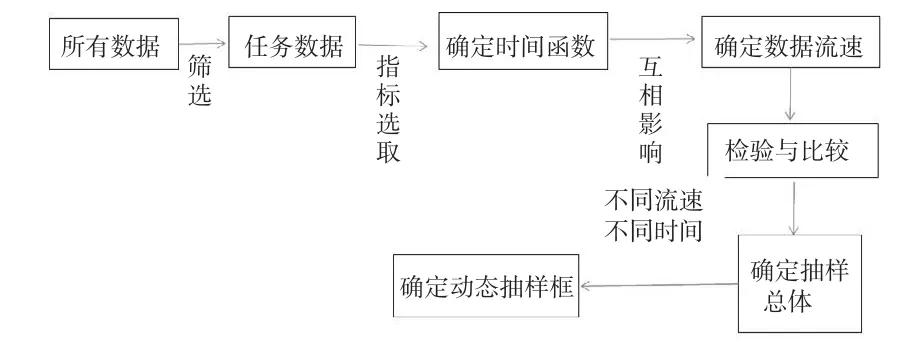
图2 动态抽样框构建的框架图
2.2 动态抽样框构建的具体步骤
(1)时间函数f(t)选择
时间函数f(t)基于不同分段节点的选择,基本原则是Ti≠Tj(i≠j,1,2,...,n)。但是由于大数据环境的复杂性,本文利用“重复等分”来确定时间节点函数f(t)。具体思路:
首先,确定研究问题的时间下限Tl和时间上限Td,即总体的时间段为[Tl,Td];然后,在[Tl,Td]内按照随机原则插入n1-1个点将总体分为n1个等间隔的时间段(间隔记为 Δt1),并利用n1来定义时间函数f1(t)=n1*Δt1;接着,在[Tl,Td]内按照随机原则插入n2-1个点,将总体分为n2个等间隔的时间段(间隔记为Δt2),并利用n2来定义时间函数f2(t)=n2*Δt2;再接着,重复上述工作,可以得到m个fk(t)=nk*Δtk(k=1,2,...,m)的函数,要求n1≠n2≠...nm;最后,利用fk(t)(k=1,2,...,m)的总体变化情况确定最终时间函数f(t),一般情况下时间总段是确定的值,即f(t)=c(常数)需要确定的是时间间隔函数Δti。
(2)流速V(t)的确定
在大数据背景下,数据的流速是瞬时万变的,本文将借助“切割”的思想,通过数学归纳法、以时间函数f(t)为依据来确定速度V(t)的变换函数。具体思路:
首先,利用步骤(1)中对f(t)的定义将整个时间段划分为n个小段,即T1=T2=...=Tn;然后,在T1中任取一个时间段(tv,ts)(满足s>v),并记录T1左侧tv时刻数据流入量为Vl(t1)、右侧ts时刻流速为Vr(t1);接着,在n-1个Ti(i=2,3,...,n)重复同样的工作,可以得到Ti段的Vl(ti),Vr(ti);并将n组左右两个时刻的流速Vl(ti),Vr(ti)(i=1,2,...,n)进行描点画线(找规律);最后,为Vl(ti),Vr(ti)拟合两条函数曲线,并找出共性,确定最终的流速函数V(t)。
(3)抽样总体N的确定
本文借助积分定理的思想,利用步骤(2)的结果将时间函数f(t)进行确定,并利用步骤(1)中的结果对流速V(t)进行确定,并在此基础上通过“切割”与“重组”的思想对抽样总体N通过求和进行确定。
3 随机模拟
假定本文研究的时间段为2017年3月1日12:00至2017年3月31日12:00为期30天,也就是Tl=2017/03/01,Td=2017/03/31,且起止时间点均为12:00。
3.1 时间函数的定义
首先确定时间函数。根据需要,假定时间函数的等间隔Δti服从如下规律(也可实际情况进行规律找寻),即Δt1=20,Δt2=1/21,Δt3=1/22...,Δtn=1/2n。关 于fi(t)=ni*Δti的部分图如图3(a)和图3(b),图3(c)为的关系图(时间长度不变)。
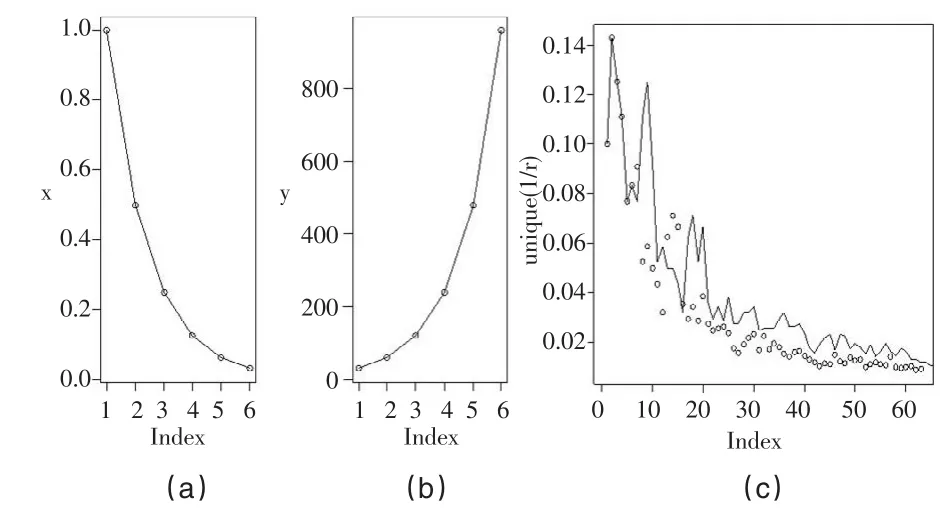
图3 时间间隔Δti和间隔数ni的关系图
3.2 流速的确定
假定n=30,则T1=T2=...=T30=1天,按照计算机模拟的随机原则对时间段内的时间节点进行选择。1天=24小时,按照数据流入时间点的特性,本文用正态分布的随机数来代替在每个Ti(1=1,2,...,30)内所选取时间“小时”的节点,再利用泊松分布产生的随机数来确定所取时间“分钟”的节点,最后,利用均匀分布的随机数来确定时间“秒”的节点(具体程序略)。按照上述的过程在R中生成的数据表及对应的Ti时间点选择如表1所示:

表1 时间函数选择结果
从表1对时间点进行对号入座,即T1段内选取的时间是1点48分38秒至2点36分20秒,T2为2点36分20秒至2点48分40秒,T3为2点48分50秒至2点54分03秒……
由于在时间段内每个时间点的数据流入量V(ti)难以确定,所以按照上文的论述只需对每个时间段Ti的所选时间的左右端点进行测量即可。在此,本文假定时间段的左右两边数据的流入量是随机的,在不假定分布的情况下,利用多种分布的随机数的混合数来进行模拟所得结果如下:
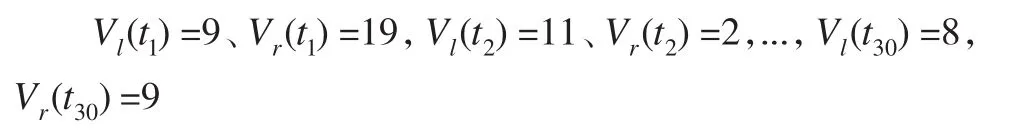
利用所得数据进行图形展示,图4(a)是全部流速数据的变化趋势图,图4(b)和图4(c)分别是左、右端点流速变化图,具体如下所示:

图4 流速变化图
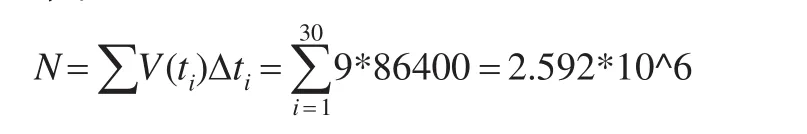
从图4(a)不难看出在95%的置信度下流速V(t)的变化区间,本文由于模拟结果比较集中,故首先选取流速的均值9作为流速的匀速值,即此刻对研究的抽样框进行计算如下:
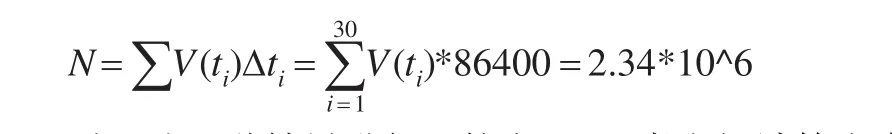
接着,按照每个小阶段的计算均值对抽样框进行计算如下:
对上述两种结果进行比较发现,二者之间计算出来的样本框的总量差距并不大,因此可以根据自身所要研究的对象对方法进行选择。
4 总结
本文根据大数据理论研究,对“大数据时代不需要抽样技术”的观点进行否定。针对大数据背景下抽样技术面临的三大挑战,给出了解决最基本问题——抽样框变动问题的方法,从抽样原理出发来分析背景不同所带来的抽样框变动的规律,进而提出构建动态抽样框的思想,并从理论和实例分析方面对大数据背景下的动态抽样框的构建进行详细说明。
不足之处在于,针对动态抽样框的构建仅仅给出时间总段函数假定不变,数据流入随机的抽样框的模拟计算,没有深入地将其他假定条件下的样本框进行构建。且仅给出动态抽样框的构建,没有对大数据背景下抽样方法的改进与应用进行讨论,这将是日后的研究方向。

