基于模糊包含度的贝叶斯粗糙集模型

魏 玲，张琬林，李 阳

（哈尔滨理工大学 经济与管理学院，哈尔滨 150040）

0 引言

波兰学者Pawlak于1982年提出的粗糙集理论是用来剖析不定性及不完整性的有效方法，可以从不完备信息中挖掘隐含知识以及潜在规律[1]。Pawlak粗糙集作为处理不确定与不精确问题的新方法，近年来迅速应用在数据挖掘和人工智能等领域，但其存在一定局限性，要求分析的类别一定是全部准确或肯定，即“包含”或“不包含”，不考虑某种程度上的“包含”或“属于”[2]。为解决其容错性能差这一缺陷问题，Ziarko于1993年对其进行了推广改进，引入容错关系提出变精度粗糙集模型[3]。在经典粗糙集模型基础上，允许在对集合进行划分时存在一定的错误分辨率以提高容错能力，当前已有大量研究成果[4-6]。在实际应用中，理想的解决方案只需根据得到的信息去处理问题，不受预先给定参数的限制，且选取不同的参数会产生不同的决策规则。为克服这种约束，Slezak等引入贝叶斯理论提出了贝叶斯粗糙集模型[7]。

由于传统粗糙集的应用对象是一般二元等价关系的信息系统，不适用自然界中的模糊信息系统，因此部分学者指出在模糊信息系统中应用粗糙集理论，最具有代表性的是Dubois等提出的模糊粗糙集模型[8]，但该模型也易受到噪声数据的干扰。为克服传统粗糙集的各种不同程度的缺陷，故将变精度粗糙集与模糊粗糙集二者相结合对学者来说具有重要研究价值。主要有以下两个研究方面：一是采用模糊理论将变精度粗糙集进行一定程度的模糊化。做出杰出贡献的学者主要有Mieszkowicz-Rolka[9]等。他在分别定义一种模糊包含集和一种错误包含度的基础上，进而将上下近似算子生成变精度模糊粗糙集（VPFRS）模型进行了重新定义；二是使模糊粗糙集精度化，主要研究学者有王丽[10]等。

本文研究发现对这类推广生成的VPFRS模型中参数的确定还有待改进。因此在VPFRS模型的基础上，引入先验概率来代替参数，提出一种基于模糊包含度的贝叶斯粗糙集（IDB-BRS）模型，也可称其为贝叶斯模糊粗糙集，进而研究了模型的基本性质和单调性，并以属性的相对重要度作为启发式信息，给出了基于该模型的属性约简算法。最后通过验证以上两种模型的属性约简结果，证明IDB-BRS属性约简是合理有效的。

1 理论基础

1.1 变精度粗糙集模型

定义1[3]：设S=(U,A,V,f)是一个信息系统，U为非空有限论域；A=C⋃D，C⋃D=∅，C为条件属性集，D为决策属性集；V是属性值的集合；f:U×A→V指研究对象的每一个属性值都存在于其所对应的相应属性之上。设X，Y为U的非空子集。如果对于每一个x∈X都有x∈Y则称X包含于Y中，记作X⊆Y。令：为X相对于Y的可信度阀值，称为X被Y包含的程度大小。

设(U,R)是近似空间，U为非空有限集合，R为U上对应的相关等价关系

1.2 贝叶斯粗糙集模型

在属性约简等实际应用中，变精度粗糙集模型中参数值的选取受决策人主观因素影响，缺乏合理性依据。因此有学者提出贝叶斯粗糙集模型，引入先验概率替代参数，对获取的信息进行高效处理[7]。

在信息系统S内，相对于X⊆U来说,E是U的相应等价关系，那么贝叶斯正域、负域、边界域分别是：

2 IDB-BRS模型及属性约简

2.1 模型构建

定义3：设U是有限非空集合，I=[0,1]，ϑ是任意蕴涵，称映射D:F(U)×F(U)→I为模糊包含度，其中I∀A,B∈F(U)。

称D(A,B)为A关于B的ϑ模糊包含度。其中ϑ选取为模糊集A的支集。

定义4：IDB-BRS模型：设U为有限非空论域，其中φ={C1,C2,…,Ck}为U的模糊覆盖之一，也是U相对于C（ii=1,2,…,k）的划分，D为模糊包含度，那么将称作模糊包含近似空间。∀X∈F(U)取那么X有关于E依的下近似以及上近似就是定义于U上的一对模糊子集：

IDB-BRS模型的正域，边界域和负域依次定义为：

2.2 模型性质

性质1：设ϑ是任意蕴涵，Ε=(F(U),φ,D)是模糊包含近似空间，那么在∀X∈F(U)中，X相对于Ε依P(X)=的 下 近 似和上近似满足条件

证明：由定义显然。

性质2：设ϑ是任意蕴涵，且满足对于∀x＞0，有成立为模糊包含近似空间，取且则有成立。

证明：由已知条件可得，∀Ci∈φ，x∈S(Ci)，有ϑ(Ci(x),0)=0成立，从而故又由性质1可得因此成立。

性质3：设ϑ是任意蕴涵，且满足对于∀x∈I，有ϑ(x,1)=1成立，Ε=(F(U),φ,D)为模糊包含近似空间，…,r且则有成立。

性质4：设ϑ是右单调蕴涵，Ε=(F(U),φ,D)是模糊包含近似空间，那么在内条件下，A,B对于Ε依的下近似及上近似满足下列性质：

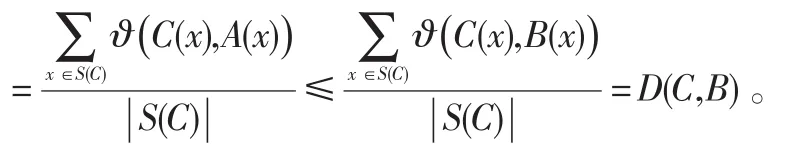
性质5：设ϑ是右单调蕴涵模糊包含近似空间，在条件下，A,B的交与并关于的下近似和上近似满足如下性质：

性质6：设ϑ是满足边界条件的左单调蕴涵，1-P(X)＜P(X)≤a内，a关于Ε依是模糊包含近似空间，在的下近似和上近似有成立。

2.3 属性约简算法

属性约简为粗糙集理论不可或缺的重要应用[11-14]，利用IDB-BRS模型对模糊决策信息系统进行相应属性约简后给出相应属性约简理论以及相关算法，并利用相关实验数据对贝叶斯模糊粗糙集属性约简算法合理性与有效性进行相关验证。

定义5：设S=(U,A,V,f)为模糊决策信息系统，U={x1,x2,…,xn}。模糊属性集B={b1,b2,…,bm}，B⊆A,则关于B的相似度为其中，xi,xj看作是B上的模糊集，xik表示xi在模糊属性bk下的隶属度，RB简称为B的模糊相似关系。xi的相似类简记为，称为由模糊相似关系RB或由属性集B诱导的模糊信息粒。

定义6：设S=(U,A,V,f)是模糊决策信息系统，其中U={x1,x2,…,xn}，A=C⋃D，C是条件属性集，D是决策属性集，B⊆C，RB,RD分别是属性集B,D的模糊相似关系，那么记其中是U的模糊覆盖，DF是U上的模糊集包含度，称Ε=(F(U),φ,D)是 模 糊 包 含 近 似 空 间 ，∀X∈F(U)取那么D有关于B的下近似分布以及上近似分布分别是：

定义7：定义U为非空论域，U={x1,x2,…,xn}，Ε=为模糊包含近似空间,A,B∈F(U)，那么则是模糊集A与B之间的分离度，且 0≤ρ(A,B)≤1。

下面利用分离度定义属性间相对重要度。

定义8：定义S=(U,A,V,f)是一个模糊决策信息系统，A=C⋃D，C是条件属性集，D是决策属性集，B⊆C，ρ则是分离度那么b∈B在B中相对于模糊决策属性集D的P(X)重要度就为则c∈C在C中相对于D的P(X)重要度为则b∈C-B关于B相对于D的P(X)重要度为C内全部相对于D的ε精度P(X)的必须属性全体，可以称作C相对于D的ε精度核，为coreP(X)(C,D,ε)。

定义9：设S=(U,A,V,f)是一模糊决策信息系统，其中A=C⋃D，C是条件属性集，D是决策属性集，B⊆C，0≤ε＜1若B满足：

则称B是C相对于D的ε精度近似约简。

属性约简为NP问题，所以不可以直接用定义对系统进行相应属性约简。下面利用属性相对重要度给出IDB-BRS模型的属性约简启发式算法。

算法：IDB-BRS模型属性约简算法

输入：模糊决策信息系统

S=(U,A=C⋃D,V,f)，模糊包含度DF，参数ε；

输出：S的一个相对约简red。

步骤1：随机选取c∈C，计算模糊相似关系Rc，RD；

步骤2：c→red；

步骤3：for任意ci∈C-red

计算sigi=sigP2(X)(ci,red,D)；

end

步骤4：选择属性cq满足

步骤5：if属性cq的重要度sigq＞ε

cq⋃red→red；

返回步骤3

else

输出red

End

为增大搜索到最小约简的概率，步骤1采用随机搜索，且在步骤4中，当选择属性cq时，若出现一个以上的属性满足时，也采用随机搜索来降低产生局部最优解的风险。在IDB-BRS属性约简算法中时间复杂度主要由步骤3和步骤4共同来决定，步骤3的时间复杂度为O(|C||U|2)，步骤4为O(|C|2|U|2)，因此，可知算法总体的时间复杂度为O(|C|2|U|2)。

3 实验及结果分析

为验证IDB-BRS属性约简具备合理有效性，将算法约简后的数据结果与文献[10]中的VPFRS生成的结果对比分析，得出结论。

3.1 实例分析

表1 模糊决策信息系统

根据表1，分别利用VPFRS和IDB-BRS得出相应属性约简结果。在VPFRS中，对参数β及ε取不同值得出的相应约简结果见表2。其中，“/”前面的数值表示500次循环后得到的所有约简中所包含的平均属性个数，“/”后面的数值表示在进行500次循环后得到最小约简所包含的属性个数。

在IDB-BRS属性约简算法中，没有参数的限制影响，约简结果只与ε精度的取值有关，根据公式，由实验数据可得出为实现与VPFRS约简结果对比的条件统一性，精度ε取相同的变化值，约简循环次数为500次，约简结果如表3所示。

表2 约简结果

表3 约简结果

由实验数据可看出，在IDB-BRS属性约简算法中，当P(X)=0.71时，在不同精度下得出属性个数比与在VPFRS属性约简算法中β=0.75时对应不同的精度得出的属性个数比结果相一致。下面比较通过约简得到的候选解项是否存在相同交集。

设B⊆C是由约简算法得到的C相对于D的ε精度约简的候选解，则称为B的质量，其中γB(D)为γB(D)对D的支持度。在VPFRS模型约简结果中，当参数β=0.75，ε=0.05时，B1={c1,c2,c3}为模糊信息系统属性约简的一个候选解。可以求得B1的D正域为对D的支持度为0.8795。C的D正域对D的支持度为得出B1的质量为0.9835。在IDB-BRS模型约简结果中，当ε=0.05时，对应得到的候选解为同理，根据公式算出B2的质量为经过对比，可得出结论候选解项具有相同交集，说明企业在进行供应链合作伙伴选择时倾向于交货运输质量高且企业技术状况良好的对象。经过实例分析可以证明得到IDB-BRS属性约简算法具备相应合理性。

3.2 UCI数据集测试

为更进一步检验IDB-BRS属性约简算法具备一定程度的有效性，选择3组UCI中常用的数据集（Soybean、Credit、Balance）来对本文提出的属性约简算法以及文献[10]中的VPFRS属性约简算法进行相关比较分析。Soybean数据集包括4个决策类，35个属性个数，样本数为307；Credit数据集包括2个决策类，15个属性个数，样本数为690；Balance数据集包括4个决策类，4个属性个数，其中样本数为625；在计算属性约简时，参数ε在区间[0.03,0.07]里选取比较合理，否则，过大会引起过度约简，过小会起不到约简的作用。因此，实验测试时取参数ε=0.05。由于VPFRS受参数的影响，为克服经验主义，从0.5到1之间等距离选取6组β值来进行实验。本次实验运行的硬件环境为Intel处理器，3.50GHz，2.00GB内存；软件环境为Windows7&MATLAB R2012a。

使用IDB-BRS属性约简算法（以下简称算法1）和文献[10]VPFRS属性约简算法（以下简称算法2）分别对3组数据集进行相应属性约简，同时记录其属性约简结果与约简运行时间，并将得到的数据集作为SVM分类器的输入，根据10折交叉验证方法输出识别结果。实验结果见表4。

表4 两种约简算法结果对比

从表4可以看出：在对数据集进行约简时，算法1得到约简个数在算法2取不同参数值得到的约简结果范围内，说明IDB-BRS模型属性约简算法是VPFRS在参数互不相同条件下所获得的属性约简的一种情况，它具备合理性。在对比分类准确率时发现算法1优于算法2，同时，由于不受参数的限制，在约简时间上也低于算法1的约简时间。综合以上数据分析，实验结果表明基于IDB-BRS的属性约简算法具备合理与有效性，且它相对于变精度模糊粗糙集而言不需要预先给定参数，在知识获取属性约简方面有实际应用价值和意义。

4 结论

由于考虑到VPFRS模型存在一定约束条件，故根据贝叶斯粗糙集和变精度粗糙集理论研究，运用先验概率替换参数推导出基于模糊包含度的贝叶斯粗糙集模型，并同时在模糊决策信息系统进行属性约简过程中运用此模型。经过对UCI数据集进行一系列实验证明此模型属性约简算法合理、有效。基于模糊包含度的贝叶斯粗糙集模型是变精度模糊粗糙集模型无参数化的高级推广方式之一，在未来实际应用中对其性质以及其属性约简算法的改进还有待进一步探究。