基于振动台电枢的界面力监测和力限振动控制试验方法及其工程应用

张 群，鲁 勇，毕京丹，张 忠，宫晓春

（北京强度环境研究所，北京 100076）

0 引言

振动试验是航天器力学环境试验的重要环节。航天产品的振动试验通常采用加速度控制，但振动台和试验夹具的机械阻抗与真实飞行状态中安装结构的机械阻抗存在很大差异；同时振动试验加速度控制的试验条件一般采用实测或预估的加速度谱包络，会导致产品和工装连接面处产生很大的界面力，特别是在试验件的共振频率处，由于动力吸振效应，界面力结果存在严重的过试验问题[1-2]，势必加大产品设计难度，增加设计成本。因此需采用加速度与界面力双重控制的力限控制方法，即在试验中同时获取和监测界面力情况[3]。现有界面力监测方法主要有力传感器法[1-3]、应变标定法[4]、加速度模态缩聚法[5]等。目前国外主要采用力传感器法直接获取界面力[6]，但对于不同接口的大型试验件，力传感器的串入将引入夹具质量、改变产品连接边界，同时传感器装置设计困难、费用高、通用性差、标定烦琐[7-8]，无法大规模应用，特别对于星箭界面和上面级等大尺寸航天产品的振动试验而言应用较为困难。

为此，针对大型舱段以及上面级产品、卫星等有效载荷振动考核中对界面力定量化试验的工程应用需求，本文在大型振动台上开展了基于振动台动圈电流电压的界面力间接获取方法研究，通过试验验证了界面力监测方法的有效性，同时建立了基于界面力评估的加速度振动控制方法，并进一步应用于星箭锁紧装置的振动试验中。

1 基于振动台电枢的界面力监测原理及振动控制方法

1.1 界面力监测方法

采用电磁振动台动圈电压电流测力法的基本原理为：星箭界面负载等的振动考核主要关心5～100 Hz的低频振动，试验条件一般为5～100 Hz的正弦扫描试验。低频振动试验时，振动台动圈等运动部件可视为刚性质量，功率放大器提供电压电流用于驱动动圈、夹具和负载等质量运动，产生的总驱动力等于星箭界面负载受到的激励力和用于使振动台动圈、夹具等运动部件运动的力之和。振动台电路模型中电流正比于驱动力，可将振动台动圈与负载看成并联电路（参见图1），由功率放大器提供的电流可分成驱动振动台动圈等运动部件的电流Id及驱动卫星等负载的电流Is。电流Id正比于振动台动圈的电压Ud，其比值为振动台动圈的导纳Yd（Yd为振动台动圈的固有属性）。同样，负载所受的界面力正比于电流Is，其比例系数Ks与负载的特性相关。因此，为了有效测量施加给卫星负载的作用力，要求测量功率放大器输出的电压和电流，并通过一系列流程测定振动台动圈导纳Yd和比例系数Ks等界面力有关参数，最终确定负载所受的界面力。

图1 振动台激振力电路模型Fig.1 Circuit model of excitation force for the shaking table

通过振动台动圈电压电流测力的具体流程如下：

1）首先不安装负载进行空台振动试验，以确定振动台动圈导纳

式中，Ie和Ue分别为空台时的输出电流和电压。

2）然后安装与试验件质量相近的刚性配重块进行振动台试验，测量配重的加速度响应，计算出负载的比例系数

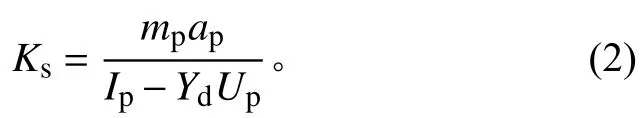
式中：Ip和Up分别为配重试验时的输出总电流和输出电压；mp和ap分别为配重块的质量和试验时的加速度。

3）最终在进行正式负载试验时，实时测量瞬时电压和电流，并计算负载所受作用力

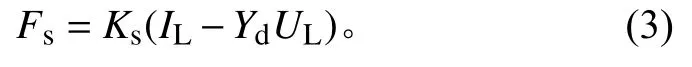
式中，IL和UL分别为正式试验的输出总电流和输出电压。

1.2 基于界面力的加速度控制方法

可通过基于准静态载荷的力限条件制定方法保守确定力限条件，即最大合力FV应不大于系统质量M乘以质心最大准静态过载aVS[6]，

界面力监测和振动控制方法的流程如图2所示。基于上述测力方法，在正式试验前，通过预试验获取负载界面力，并由式(4)评估正式试验时界面力的过载情况，如果质心加速度aCG计算值超过设计载荷，就需对加速度试验条件进行修改，根据界面力情况通过手动带谷或响应限值进行振动加速度控制，以确保产品安全。

图2 界面力监测和振动控制流程Fig.2 Procedure of interface force monitoring and vibration control

2 试验验证及分析

为验证动圈电压电流测力法的正确性，分别在350 kN的滑台和垂台（带扩展台）上进行验证试验。按表1的正弦振动试验条件谱形依次在垂台和滑台上进行空载和带刚性配重的振动试验。其中：垂台空载时按谱形进行了1.0g、1.2g和1.5g三个量级的振动试验，并分别采用质量692、932和1366 kg的刚性配重进行了量级为1.5g的振动试验；滑台空载时进行了0.9g、1.5g和1.8g三个量级的振动试验，并分别采用质量692、932和1366 kg的刚性配重进行了量级为1.8g的振动试验。各工况下均对动圈电压电流、刚性质量块的加速度进行了测量。

表1 正弦扫描振动试验条件谱形Table 1 Spectrum under sine vibration test condition

图3为垂台和滑台空载时不同量级条件下按式(1)计算的振动台动圈导纳对比。由图可知，垂台和滑台不同量级计算的振动台动圈导纳均相同，验证了振动台动圈导纳为振动台动圈的固有属性。

图3 垂台与滑台空载不同试验量级下的振动台动圈导纳对比Fig.3 Moving coil admittance of the vertical and the sliding tables at different test levels with empty load

图4为垂台和滑台不同质量配重条件下按式(2)计算的负载比例系数对比。由图可知，对于刚性配重，垂台和滑台电流电压的信噪比均随配重质量增大而增大，比例系数频域曲线的偏差波动较小，较为光滑，且不同配重计算的比例系数基本相同。

图4 垂台和滑台在不同配重下的负载比例系数计算结果Fig.4 Scaling factor of workload for the vertical and the sliding tables with different mass simulators

依次将932 kg和1366 kg配重视为负载并结合空台的试验数据进行界面力预测的相互验证。图5为垂台和滑台由空台和932 kg配重的试验结果按式(3)预测的负载为1366 kg时的界面力结果，并将其与由配重加速度按aCG计算的配重质心处惯性力进行对比。对于刚性配重，惯性力即为界面力的准确值，原则上界面力预测值应与惯性力相等。由试验曲线对比结果可知二者基本一致，仅在高频有一定的偏差，满足对界面力量级估计的误差要求。

图5 垂台和滑台1366 kg配重的界面力预测结果Fig.5 Predicted interface force on the vertical and the sliding tables with 1366 kg mass simulator

图6为垂台和滑台由空台和1366 kg配重的试验数据预测的负载为932 kg时的界面力结果，及其与配重质心处惯性力的对比。由图中的对比结果可知，预测的界面力也与惯性力基本一致。另外，注意到由于轴向采用扩展台、大推力振动台较为老旧和研制的电压电流测量设备灵敏度和信噪比较低等综合因素，图6中轴向试验的界面力在50～70 Hz间存在较大偏差，最大可达25%，但该偏差与过试验问题的量级程度（超出数倍以上）相比可以忽略，不妨碍降低过试验的目标达成。因此，可以认为基于动圈电压电流的界面力预测方法的正确性得到验证。

图6 垂台和滑台932 kg配重的界面力预测结果Fig.6 Predicted interface force on the vertical and the sliding tables with 932 kg mass simulator

3 星箭锁紧装置振动考核应用

应用上述界面力监测和振动控制方法，针对星箭锁紧装置振动试验考核中对界面力监测和定量化试验的需求，开展了2种大型星箭锁紧装置的振动试验。

图7为星箭锁紧装置（包带）振动试验示意图。试验件均由模拟星、星箭锁紧装置构成，并与转接工装及振动台组成振动试验系统。A型包带试验件的总质量为3.09 t，包带直径约为940 mm，试验件质心高度为1670 mm。该型包带的特点为模拟星为刚性较大的集中质量块，通过特性试验确定该型包带试验件的轴向一阶固有频率大于试验频率上限（100 Hz），横向一阶固有频率为11 Hz。B型包带试验件的总质量为5.5 t，包带直径约为2400 mm，试验件质心高度为2200 mm。该型包带的特点为模拟星为中空薄壁桶状结构，上部具有集中质量，试验件横向和纵向的一阶固有频率均在100 Hz内，试验频率范围内为柔性结构。

图7 星箭锁紧装置振动试验Fig.7 Vibration test for two types of satellite-rocket locking devices

基于产品质量大、质心高、直径大的特点，如前所述采用力传感器法监测界面力较为困难，应用本文提出的动圈电压电流测力法进行界面力获取和振动控制，按照图2的监测和控制流程，其中：A型包带按照表2的正式试验条件分别进行了轴向和横向的振动试验；B型包带按照表1的试验条件谱形进行试验，轴向量级为1.2g、横向量级为0.9g。A、B两型包带均在模拟星质心高度处外表面安装加速度传感器，由测得的加速度与试验件质量的乘积计算惯性力。

表2 A 型星箭锁紧装置振动试验条件Table 2 Spectrum under sine vibration test condition for the satellite-rocket locking device of type A

图8为正式试验时A型包带轴向和横向界面力预测值与惯性力计算值的对比。由于模拟星为集中质量且试验件在试验范围内为刚性，质心高度处传感器获得的加速度与真实质心加速度基本一致，所以可将惯性力计算值视为界面力的准确值[9]。由图8(a)的轴向结果可知，界面力预测值基本与惯性力相等，由于轴向试验频率范围内无共振频率，进一步验证了刚性负载时动圈电压电流测力法的正确性；由图8(b)的横向结果可知，极大值处界面力预测值与惯性力相等，极小值的波谷附近界面力预测值大于惯性力。这是由于现有电压电流测量设备的灵敏度较低，噪声掩盖了信号的极小值，但这不影响力限监测关注的极大值信息；另外与模拟配重时原因相同，轴向试验在50～70 Hz间存在较大偏差，最大可达32%，但该偏差与过试验问题的量级（超出数倍以上）比较可以忽略，不妨碍降低过试验的目标达成。这也验证了对试验频率内存在一阶柔性结构的界面力监测的合理性。在预试验后评估包带的界面力未超设计载荷，该型包带最终顺利完成了振动试验考核。

图8 A型包带轴向和横向界面力预测结果Fig.8 Predicted interface force for the satellite-rocket locking device of type A in x and y directions

图9为0.1g量级预试验时B型包带轴向和横向界面力预测值与惯性力计算值的对比。由图9(a)可知，在试验频率范围内，包带产品的轴向界面力存在2个峰值，最大峰值频率为56.2 Hz；界面力预测值与惯性力计算值在低频的刚体位移段基本相等，在最大峰值处惯性力计算值比界面力预测值大近1倍（如表3所示），而二者的波谷位置也不一致。这是因为柔性结构振动过程的实际质心无法确定，仅在低频段结构视为刚体时可近似等于未变形时的质心，导致计算的惯性力存在不确定性。由上文已知，由于噪声和灵敏度问题，界面力的计算值在波谷处也不尽准确，但这不影响对峰值的估计和力限试验目的实现。横向试验结果的规律与轴向试验相同。总体而言，柔性结构的质心加速度往往无法测量[9]，采用动圈电压电流测力法能满足对界面力的监测要求，同时试验易于实施，通用性较好。

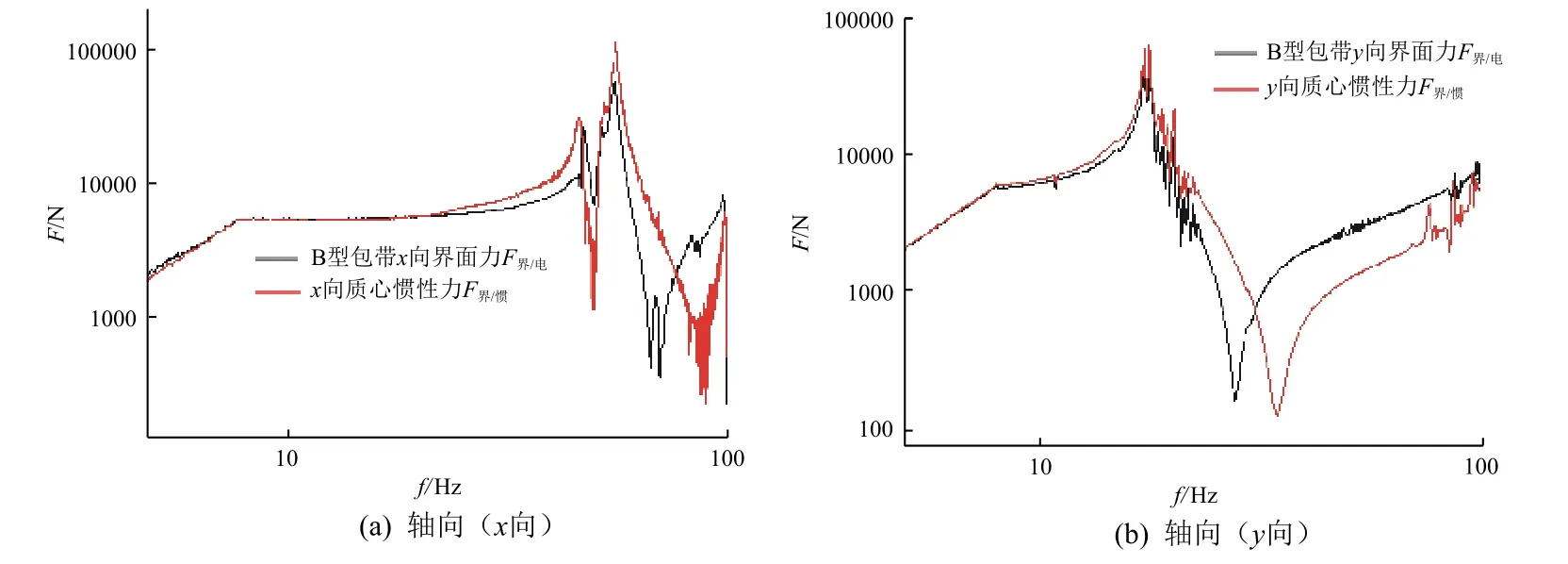
图9 B型包带轴向和横向界面力预测结果Fig.9 Predicted interface force for the satellite-rocket locking device of type B in x and y directions

表3 B 型包带界面力峰值对比Table 3 Peak value of interface forces for the satellite-rocket locking device of type B

根据预试验界面力的计算结果对B型包带进行加速度控制：包带界面力的设计载荷为轴向时400 kN、横向时200 kN，预计满量级试验时轴向和横向界面力都将超出设计载荷，存在过试验风险，需进行带谷控制。因此，轴向时对加速度条件在56 Hz附近下凹6 dB，横向时对加速度条件在17.9 Hz附近下凹7 dB，然后进行正式量级的试验，最终顺利完成B型包带的振动试验。

4 结束语

本文基于振动台动圈电压电流建立了界面力获取的电路模型和界面力预测方法，并通过实际大型振动台的空载试验、配重试验验证了方法的正确性——对于刚性配重，界面力测量具有较好的一致性。同时通过两型包带振动试验进一步验证了该方法对实际航天产品和柔性结构的适用性，结合界面力获取数据，制定了包带振动试验加速度控制与界面力评估相结合的控制方法，达到力限控制的目的，提高了航天器地面振动试验模拟的真实性。

本文的界面力监测和振动控制方法操作简单、不改变产品状态、试验成本低、通用性较好，能满足大型舱段以及上面级产品、卫星等有效载荷的振动考核中对界面力的定量化试验需求，对复杂星箭系统、上面级等大型航天产品的精细化设计和试验验证具有指导意义。