预测视角下双因子模型与高阶因子模型的一般性模拟比较*

温忠麟 汤丹丹 顾红磊



预测视角下双因子模型与高阶因子模型的一般性模拟比较

温忠麟汤丹丹顾红磊

(华南师范大学心理应用研究中心/心理学院, 广州 510631) (信阳师范学院教育科学学院, 信阳 464000)

高阶因子模型本质上是一种特殊的双因子模型, 应用中却常被当做双因子模型的竞争模型。已有研究以满足比例约束的双因子模型(此时等价于一个高阶因子模型)为真实测量模型产生模拟数据, 比较了用双因子模型和高阶因子模型作为测量模型的预测效果。本文使用不满足比例约束的双因子模型(此时不与任何高阶因子模型等价)为真实测量模型产生模拟数据进行比较, 所得结果与满足比例约束的双因子模型的结果有很大差别, 双因子模型结构系数的相对偏差较小、检验力较高, 但第Ⅰ类错误率略高。结论是, 在比例约束条件成立时可以使用高阶因子模型, 否则, 从统计角度看, 一般情况下使用双因子模型进行预测比较好。

结构系数; 双因子模型; 高阶因子模型; 比例约束

1 引言

在心理、教育、管理等研究领域, 常用双因子模型(bifactor model)、高阶因子模型(high-order factormodel)拟合多维构念(multidimensional construct)。随着双因子模型的应用领域不断扩大, 不少研究者推荐使用双因子模型拟合多维构念 (Chen, Hayes, Carver, Laurenceau, & Zhang, 2012; Cucina & Byle, 2017; Hyland, Boduszek, Dhingra, Shevlin, & Egan, 2014; Salerno, Ingoglia, & Coco, 2017) 。

数理上, 高阶因子模型嵌套于双因子模型, 在负荷满足比例约束(proportion constrain)时, 两种模型等价(Schmid & Leiman, 1957; Yung, Thissen, & Mcleod, 1999)。此时, 一个高阶因子对应于一个全局因子, 解释所有题目的共同变异; 一阶因子被高阶因子解释后的残差对应于局部因子, 表示被全局因子解释后测量该因子的那些题目的共同变异(Chen, West, & Sousa, 2006)。一般情况下, 即不满足比例约束的条件下两种模型并不等价(Gustafsson & Balke, 1993; Schmid & Leiman, 1957), 但研究者常把两种模型作为竞争模型(Chen, et al, 2012; Chen, Jing, Hayes, & Lee, 2013; Cucina & Byle, 2017; Gu, Wen, & Fan, 2017a; Hyland, et al., 2014)。Chen等人(2006)基于实测数据比较了效标为显变量时, 两种模型的拟合指数和结构系数(structural coefficient, 又称效度系数)。徐霜雪、俞宗火和李月梅(2017, 后面简称徐文)模拟研究了效标分别为显变量和潜变量时, 两种模型的拟合指数和结构系数偏差。但徐文的研究目的和结论中所提到的双因子模型是一般的双因子模型, 而在其模拟研究中所使用的双因子模型却是满足比例约束的双因子模型(此时等价于一个高阶因子模型)。

如要一般地比较双因子模型和高阶因子模型, 真模型应该有两个——满足比例约束的双因子模型(此时等价于一个高阶因子模型)、不满足比例约束的双因子模型(此时不等价于任何一个高阶因子模型)。对于前一种真模型产生的数据(徐文已做), 无论用双因子模型还是高阶因子模型去拟合, 都是拟合了真模型; 而对于后一种真模型产生的数据(徐文未做), 用双因子模型是拟合了真模型, 用高阶因子模型则拟合了误设模型。

两种模型参数估计和检验的比较, 徐文只是比较了结构系数估计的相对偏差。其实还应当比较统计检验力、第Ⅰ类错误率(例见Gu, Wen, & Fan, 2017b;Wu, Wen, Marsh, & Hau, 2013), 才能做出比较全面的评价。此外, 徐文的模拟中将结构系数固定不变, 其实结构系数也作为模拟实验的条件进行设计比较好。而且, 为了比较检验力和第I类错误率, 这样的设计是必须的。本文增加了这方面的工作。

本文将通过蒙特卡洛(Monte Carlo)模拟, 用两种双因子模型(满足和不满足比例约束)产生数据, 研究效标分别为潜变量和显变量时, 双因子模型和高阶因子模型在预测视角下的表现, 系统比较结构系数的相对偏差、统计检验力、第Ⅰ类错误率等。

2 模型概述

2.1 双因子模型

双因子模型又称为全局−局部因子模型(general-special factor model), 如图1中的M所示。双因子模型假设同时存在全局因子(general factor)和局部因子(special factor), 全局因子解释所有题目的共同变异; 局部因子解释控制了全局因子后部分题目(测量了一个维度)的共同变异(Chen, et al., 2006; 顾红磊, 温忠麟, 2017)。该模型在很多领域都有应用, 如管理心理学、健康心理学、教育心理学等(Distefano, Greer, & Kamphaus, 2013; Howard, Gagné, Morin, & Forest, 2018; Wang, Fredricks, Hofkens, & Linn, 2016)。

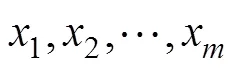
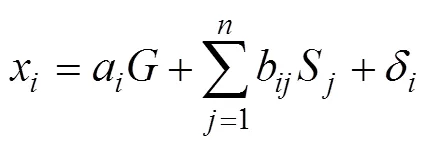
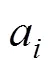
该模型假设全局因子和局部因子不相关, 局部因子之间可以相关; 误差与全局因子、局部因子不相关, 且误差之间不相关。若局部因子之间也不相关, 则为正交双因子模型。和徐文一样, 本研究采用有3个局部因子、每个局部因子4个指标的正交双因子模型。

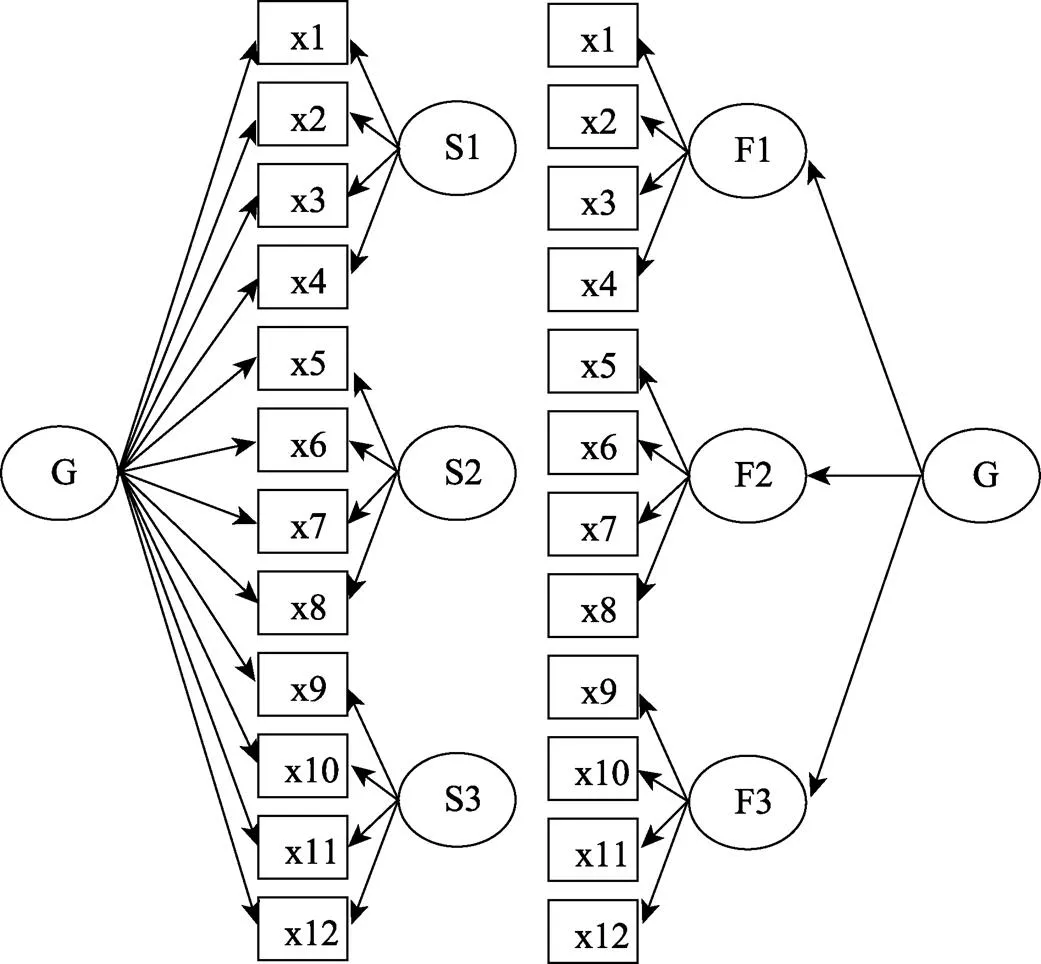
图1 双因子模型M1和高阶因子模型M2

2.2 高阶因子模型

常见的高阶因子模型是二阶因子(second-order factor)模型, 如图1中的M所示。高阶因子解释全部一阶因子(维度)的共同变异, 一阶因子解释相应维度的一组题目的共同变异(顾红磊, 温忠麟, 2017)。

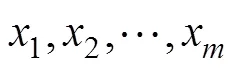
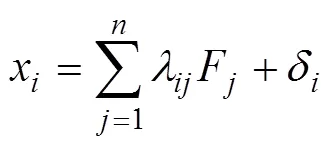
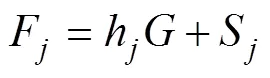
其中,λ是题目x在一阶因子F上的负荷,δ是题目x的测验误差;h是一阶因子F在高阶因子上的负荷,S是一阶因子F被高阶因子解释后的残差(简称为一阶因子的残差), 对应于双因子模型中的局部因子, 故两者都用符号表示。该模型假设误差间不相关。本研究采用有3个一阶因子, 每个一阶因子4个题目的高阶因子模型。

2.3 两种模型的关系

高阶因子模型嵌套于双因子模型(Schmid & Leiman, 1957; Yung, et al., 1999), 任何一个高阶因子模型都可以转化为一个双因子模型。原来的高阶因子变成了全局因子, 一个题目x在全局因子上的负荷a等于该题目在一阶因子F上的负荷λ乘以该一阶因子在高阶因子上的负荷h, 即a=λh; 一阶因子F被高阶因子解释后的残差S变成了局部因子, 即一阶因子的残差相当于局部因子, 题目x在局部因子S上的负荷就等于该题目在一阶因子上的负荷λ, 这不难将公式(3)代入公式(2)并与公式(1)比较推导出来(Demars, 2006; Schmid & Leiman, 1957)。

Schmid和Leiman (1957)证明在满足比例约束时, 两种模型是等价的。比例约束是指, 在每个维度中, 全局因子的负荷和局部因子的负荷之比等于一个常数, 此常数为一阶因子在高阶因子上的负荷h, 但不同维度中这个常数可以不同。然而, 一般的双因子模型是不满足比例约束条件的, 实际中也很难找到多维构念恰好可用满足比例约束条件的双因子模型去拟合。例如, 在期刊发表的关于双因子模型应用的文章中, 有33篇论文报告了因子负荷, 没有一个双因子模型是满足比例约束的。

2.4 预测视角下两种模型的关系

在双因子模型中, 全局因子作为预测变量表示所有题目的共同特质对效标的作用, 局部因子作为预测变量表示在控制了全局因子的影响后, 部分题目的额外共同特质对效标的作用, 如图2所示。当有个局部因子时, 公式为

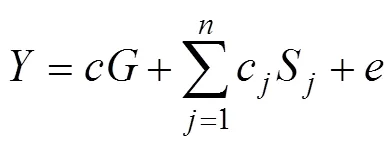
其中,表示全局因子对效标的效应大小,c表示局部因子S对效标的效应大小,表示预测残差。这里的效应就是所谓的结构系数。Mplus程序见附录1。

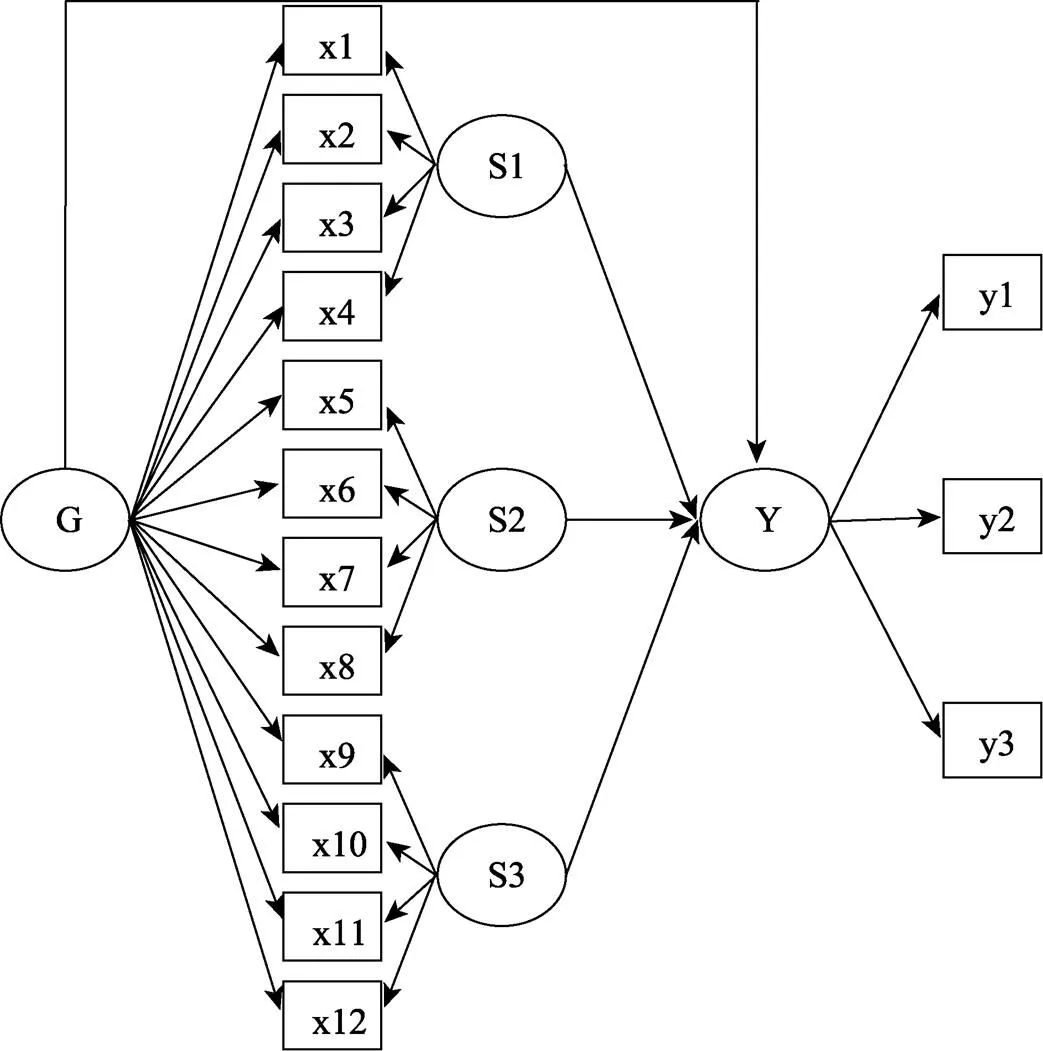
图2 双因子模型M对效标变量的预测

在高阶因子模型中, 虽然可以直接考虑高阶因子和一阶因子对效标的作用, 但为了跟徐文的相应模型一致, 先建立如下模型。在高阶因子模型中, 高阶因子作为预测变量表示一阶因子之间的共同特质对效标的作用, 一阶因子的残差(正是双因子模型的局部因子)作为预测变量表示部分题目的额外共同特质对效标的作用, 如图3所示。当有个一阶因子时, 公式为

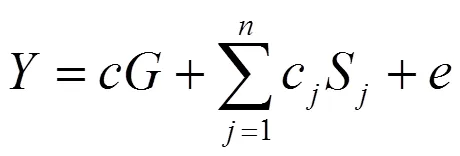
其中,表示高阶因子对效标的效应大小,c表示一阶因子的残差S对效标的效应大小,表示预测残差。

图3 高阶因子模型M对效标变量的预测

对于上述高阶因子建模, EQS软件可以直接使用一阶因子的残差作为预测变量(Bentler, 1995), 但Mplus软件仅可以使用一阶因子作为预测变量(Muthén & Muthén, 2012)。把公式(3)代入公式(5)可得

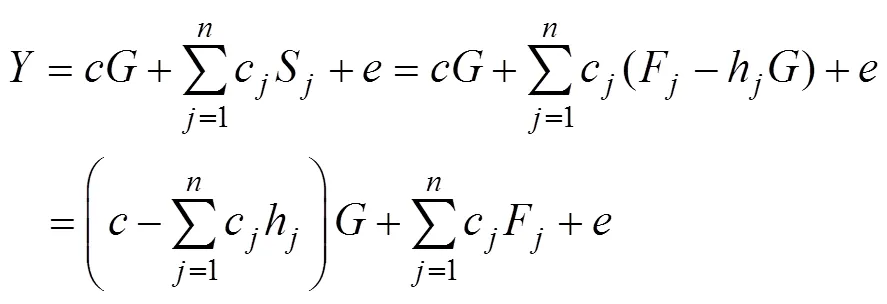
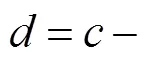
3 模拟研究

我们首先重复了徐文的模拟研究, 即真模型是满足比例约束的双因子模型。无论效标变量是显变量还是潜变量, 在估计偏差上得到的结果与徐文高度一致, 即满足比例约束的情形, 高阶因子模型结构系数的相对偏差比较小。此外还发现, 检验力方面, 若真模型是全局因子和局部因子同时作为预测变量, 整体上双因子模型的统计检验力较高。相应地, 无论真模型是全局因子还是局部因子作为预测变量, 都是高阶因子模型的第Ⅰ类错误率较小。为了节省篇幅, 这里不报告细节。

下面报告真模型为不满足比例约束的双因子模型的模拟研究, 这是徐文没有做的情形。虽然我们也考虑了效标为潜变量和显变量的两种设计, 但因为两种设计的结果高度一致, 所以下面只报告效标为潜变量的情形, 与徐文的一样, 效标潜变量有3个指标、标准化的负荷固定为比较有代表性的0.7 (也见Gu et al., 2017b)。模拟研究设计主要是针对预测变量的测量模型进行。

3.1 研究设计

真模型为不满足比例约束的双因子模型, 由符合下列条件的双因子模型M产生数据, 为与徐文对比, 参数设计尽量与徐文的设计一致, 但本文对结构系数也做了设计(在考虑用检验力和第I类错误率进行评价时是必须的)。

(1) 全局因子的负荷：0.4, 0.5, 0.6和0.7。全局因子共12个题目, 每种条件下, 全部12个题目在全局因子上的负荷都相等(Reise, Scheines, Widaman, & Haviland, 2013; 徐霜雪等, 2017)。不满足比例约束条件的双因子模型的一个充分(但不必要)条件是, 不同题目在同一个局部因子上的负荷各不相等, 但在全局因子上的负荷相等。M每个局部因子的4个题目, 其负荷分别设置为0.4, 0.5, 0.6, 0.7。

(2) 全局因子和局部因子的结构系数设置了三种组合：0.3、0.3; 0、0.3; 0.3、0。例如, 0、0.3表示全局因子对效标的效应为0, 3个局部因子对效标的效应都是0.3。

(3) 样本容量： 200, 500和1000。

(4) 用于估计的模型：双因子模型M和高阶因子模型M。

本模拟实验是4×3×3×2的混合设计, 前3个因素都是被试间因素, 最后一个因素是被试内因素。对于被试间因素, 共有36种水平组合。使用Mplus 7.4模拟生成1000个样本数据, 即每种组合重复1000次。

全局因子负荷、局部因子负荷、结构系数、样本容量为条件, 估计的模型——双因子模型和高阶因子模型为关注对象。据此可以在不同数据条件下进行比较, 包括模型拟合程度、结构系数的相对偏差、统计检验力、第Ⅰ类错误率, 还可以了解当全局因子和局部因子负荷、样本容量变化时, 比较指标的变化。

3.2 结果

本文除了和徐文一样报告了样本容量为1000的结果外, 同时报告样本容量为500和200的结果。

3.2.1 适当解

排除不恰当解的结果, 如不收敛、方差和标准误为负的情形, 仅考虑恰当解的情况。样本容量为1000时, 两种模型的收敛率都在99%以上。随着样本容量减少, 两种模型的收敛率降低, 但都在92%以上, 最大相差6%。同种情况下, 高阶因子模型的收敛率高于双因子模型。

3.2.2 模型拟合

一般认为, CFI (comparative fit index)和TLI (Tucker-Lewis Index)大于0.9, RMSEA (Root Mean Square Error of Approximation)和SRMR (Standardized Root Mean square Residual)小于0.08, 则模型整体拟合良好(Marsh, Hau, & Wen, 2004; 温忠麟, 侯杰泰, 马什赫伯特, 2004)。信息指数AIC、ABIC越小, 则模型拟合越好(Burnham & Anderson, 1998)。所有条件下, 双因子模型拟合较好。虽然高阶因子模型拟合比双因子模型差, 但也达到了拟合良好的标准。

3.2.3 结构系数的相对偏差

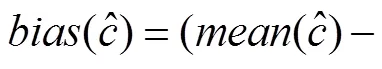
由于三个局部因子(一阶因子的残差)为预测变量时, 三条路径作用相同, 这里只考虑其中一条路径(S1因子的结构系数)的结果, 如图4所示。双因子模型结构系数的相对偏差比高阶因子模型的普遍较小, 但存在交互作用：样本容量较小而且全局因子负荷较低时, 双因子模型结构系数的相对偏差较大; 样本容量较大时, 双因子模型结构系数的相对偏差较小。85%的处理中, 双因子模型结构系数的相对偏差小于10%。随着样本容量的增加, 整体上两种模型结构系数的相对偏差变小。此外, 全局因子负荷越大, 双因子模型结构系数的相对偏差越小。

3.2.4 统计检验力

统计检验力(power)是指真值不为0时, 估计值显著不等于0的概率。统计检验力越接近1越好。由图5可见, 在所有条件下, 都是双因子模型的统计检验力比较高。样本容量越大, 两种模型的统计检验力都越高。此外, 全局因子负荷越大, 两种模型的统计检验力都越高。

3.2.5 第I类错误率

第I类错误率(type I error rate)是指真值为0时, 估计值显著不等于0的概率。一般认为第I类错误率越接近真值0.05越好, 在0.025~0.075之间是可以接受的(Bradley & James, 1978; Mackinnon, Lockwood, & Williams, 2004; Wu et al., 2013)。

和检验力的结果类似, 双因子模型的第I类错误率比较大(见图6)。当= 1000时, 在模拟的各种条件下两种模型的第I类错误率几乎都在可接受范围。但在样本容量较小而且全局因子负荷较低时, 双因子模型的第I类错误率大于可接受的范围。全局因子负荷越大, 双因子模型的第I类错误率越接近0.05。

3.3 小结

本模拟研究是徐文没做的一个新研究, 产生数据的双因子模型不等价于任何一个高阶因子模型。多数情况下, 双因子模型结构系数的相对偏差比较小, 尤其是当= 1000的时候, 双因子模型一致小于高阶因子模型。但在小的时候, 两种模型的相对偏差大小比较没有一致的结果, 尤其是全局因子的负荷较小时。检验力方面, 各种情况下都是双因子模型的比较高。相应地, 无论真模型是全局因子还是局部因子作为预测变量, 都是双因子模型的第I类错误率比较大。

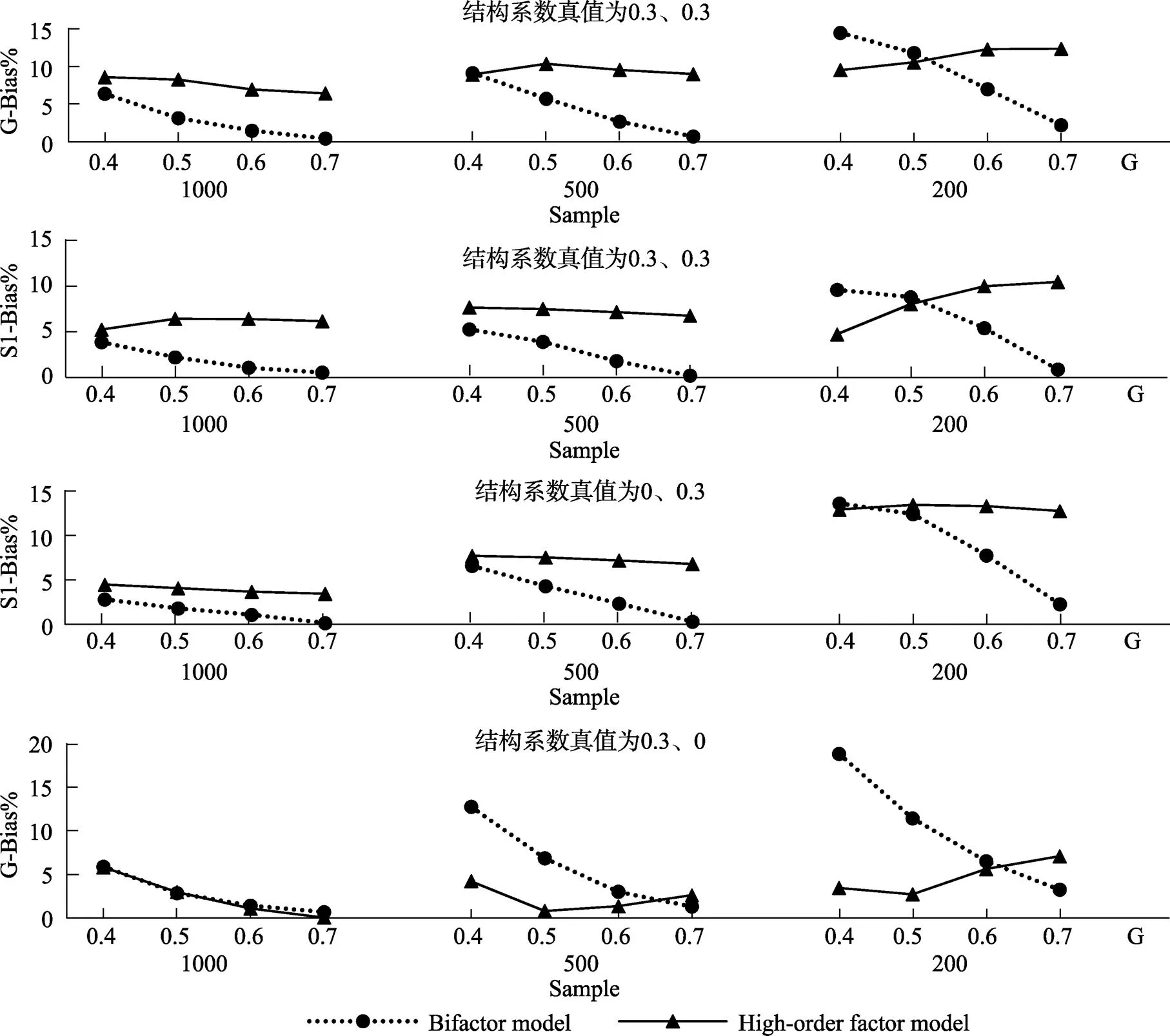
图4 不满足比例约束条件时结构系数的相对偏差

注：横轴G表示全局因子负荷(下同); 纵轴G-Bias%表示G因子的结构系数的相对偏差; S1-Bias%表示S1因子的结构系数的相对偏差。

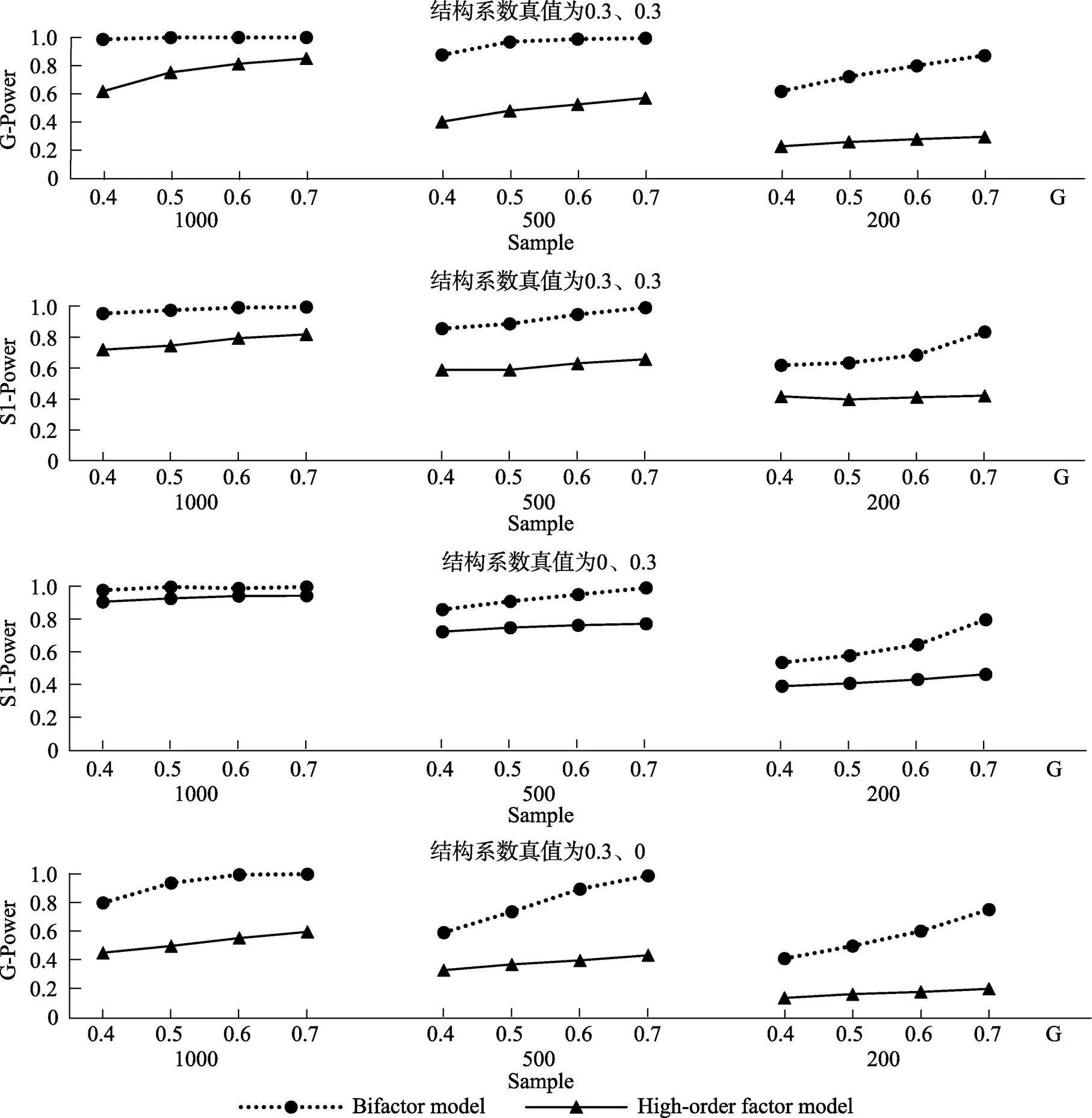
图5 不满足比例约束条件时结构系数的统计检验力

注：G-Power表示G因子的结构系数统计检验力, S1-Power表示S1因子的结构系数统计检验力。

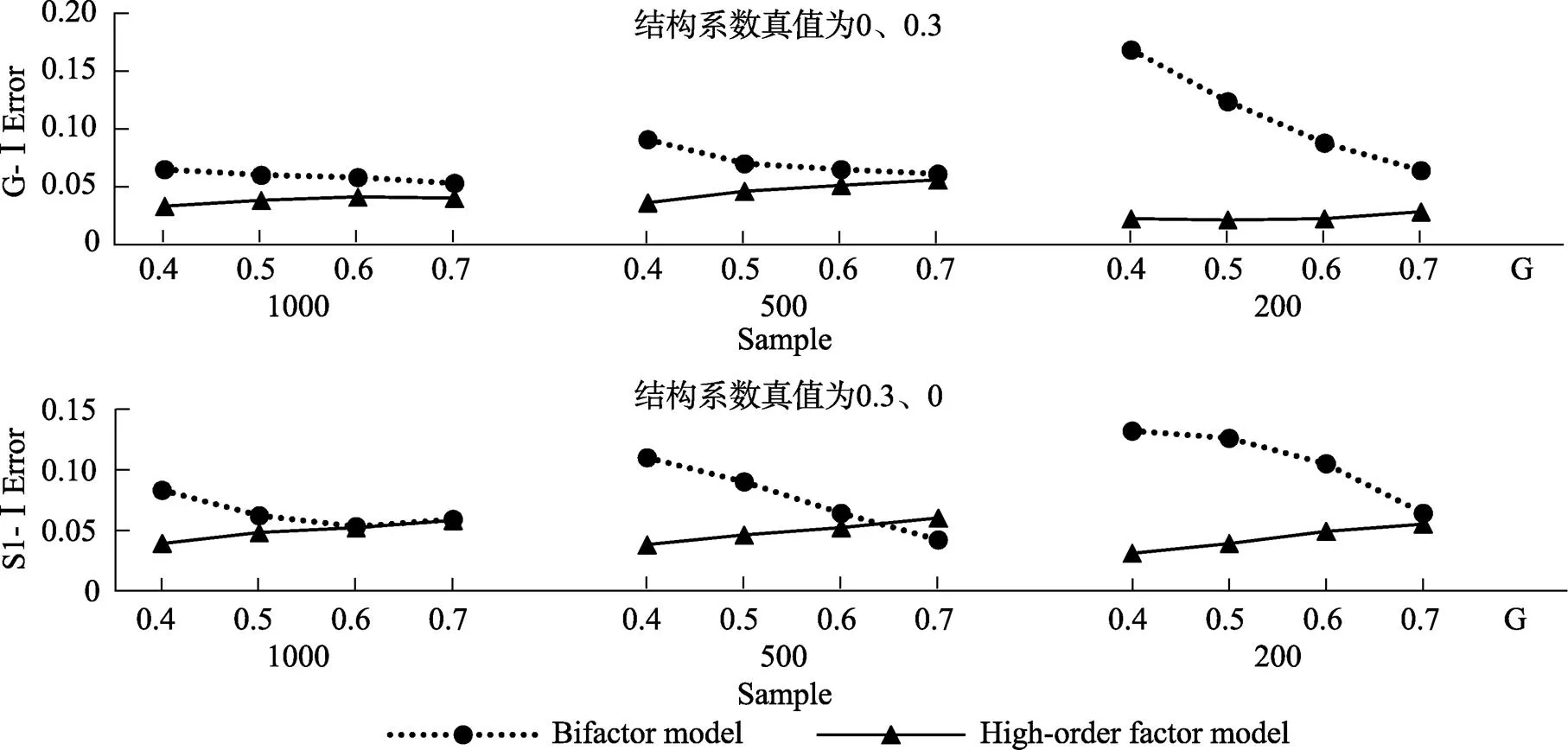
图6 不满足比例约束条件时结构系数的第I类错误率

注：G-I Error表示G因子的结构系数的第I类错误率, S1-I Error表示S1因子的结构系数的第I类错误率。

4 结论和讨论

徐文研究以满足比例约束的双因子模型(此时等价于一个高阶因子模型)为真实测量模型产生模拟数据, 比较了用双因子模型和高阶因子模型作为测量模型的结构系数。在其研究中, 无论使用的是双因子模型还是高阶因子模型, 都是拟合了真模型。本文使用不满足比例约束的双因子模型为真实测量模型产生模拟数据进行比较, 无论结果是否与徐文相同, 都是有意义的。徐文的模拟研究结果只能说明, 满足比例约束条件时, 高阶因子模型结构系数的相对偏差更小。但一般情况下比例约束条件是不满足的, 在此种情况下, 如果徐文的结果还正确, 则可将徐文结果推广到很一般的范围; 如果徐文结果不再正确, 则本文的意义更大。此外, 本文从多角度比较了两种模型的表现, 包括拟合指数、结构系数的相对偏差、统计检验力、第I类错误率。

当真模型满足比例约束条件时, 与双因子模型相比, 高阶因子模型结构系数的相对偏差较小(这和徐文的结果一致); 第I类错误率较低, 但检验力也较低。两种模型的拟合程度差别不大, 都达到拟合良好的标准。考虑到高阶因子模型比较省检(自由度更大), 当模型满足或近似满足比例约束条件时, 首选高阶因子模型进行预测, 尤其是样本容量较大时, 检验力较低的缺点会消失。

当真模型不满足比例约束条件时, 使用高阶因子模型可以说是拟合了误设模型。即使高阶因子模型的拟合指数还是可以接受, 但比双因子模型拟合要差。更重要的是, 与高阶因子模型相比, 双因子模型结构系数的相对偏差普遍较小, 尤其是当较大的时候。这与徐文的结果正好相反, 所以徐文的结果没有普遍性。此外, 各种情况下都是双因子模型的统计检验力较高, 相应地, 第I类错误率也略高(尤其样本容量比较小的时候)。总之, 当模型不满足比例约束条件时(通常的应用属于此种情况), 从统计角度不能说高阶因子模型比双因子模型还好。

那么, 是不是在预测视角下, 就优先考虑双因子模型呢？也不是, 而是应当从学科理论出发、结合研究目的选用模型。与双因子模型相比, 高阶因子模型不仅更加简洁, 而且其中的一阶因子比局部因子更容易理解。如果研究者使用高阶因子模型进行预测, 而整个模型已经拟合良好, 且各项评价指标也达到要求, 是可以接受的。但高阶因子模型可以接受, 并不能说它优于双因子模型。

高阶因子模型的高阶因子定义在一阶因子上而非观测变量(题目)上, 因此高阶因子对观测变量没有直接效应, 一阶因子相当于中介变量, 高阶因子对观测变量的作用完全通过一阶因子的作用实现(Gignac, 2008; 顾红磊, 温忠麟, 2017)。而双因子模型的全局因子和局部因子都直接定义在观测变量上, 对观测变量都是直接效应, 有时候更易解释全局因子、局部因子和效标变量之间的关系(Beaujean, Parkin, & Parker, 2014; Chen et al., 2006)。特别是当使用高阶因子模型结果不理想的时候, 双因子模型是值得考虑的替代模型。

本研究中发现若不满足比例约束条件, 样本容量为1000时, 双因子模型的第I类错误率基本上可以接受; 样本容量为500时, 近六成的处理中双因子模型的第I类错误率都在可接受的范围内。因此, 使用双因子模型时样本宜大一些, 比如不小于500。此外, 高阶因子模型尤其是双因子模型较难收敛, 样本容量越大越有助于提高收敛性, 而且大样本(如超过500)得到的预测偏差基本上在可接受范围, 也有较高的检验力。

有时候根据常用的拟合指数可能不知道是用双因子模型还是高阶因子模型拟合多维构念较好, 但模拟研究发现满足比例约束的双因子模型和不满足比例约束的双因子模型的信息指数(例如, AIC、ABIC)表现不一。对于AIC和ABIC, 满足比例约束条件时双因子模型的比较大, 而不满足比例约束条件时高阶因子模型的比较大。在实证研究中, 可以通过比较两种模型的AIC和ABIC判断哪个更适宜拟合多维构念。如果双因子模型的AIC、BIC较大, 倾向于选用高阶因子模型, 否则考虑使用双因子模型研究结构系数, 也便于进一步解释多维构念与效标之间的关系。

为了比较徐文结果, 本研究与徐文一样使用正交双因子模型。但正交双因子模型假设局部因子间不相关。在更一般的情况下, 即双因子模型的局部因子允许相关, 本研究结果是否全部成立, 有待进一步研究。

Beaujean, A. A., Parkin, J., & Parker, S. (2014). Comparing Cattell-Horn-Carroll factor models: Differences between bifactor and higher order factor models in predicting language achievement.(3), 789–805.

Bentler, P. M. (1995).. Encino, CA: Multivariate Software.

Bradley, & James, V. (1978). Robustness?, 144–152.

Burnham, K. P., & Anderson, D. R. (1998).. New York, NY: Springer.

Chen, F. F., Hayes, A., Carver, C. S., Laurenceau, J-P., & Zhang, Z. (2012). Modeling general and specific variance in multifaceted constructs: A comparison of the bifactor model to other approaches.(1), 219–251.

Chen, F. F., Jing, Y., Hayes, A., & Lee, J. M. (2013). Two concepts or two approaches? A bifactor analysis of psychological and subjective well-being.(3), 1033–1068.

Chen, F. F., West, S. G., & Sousa, K. H. (2006). A comparison of bifactor and second-order models of quality of life.(2), 189–225.

Cucina, J., & Byle, K., (2017). The bifactor model fits better than the higher-order model in more than 90% of comparisons for mental abilities test batteries.(3), 27.

Demars, C. E. (2006). Application of the bi-factor multidimensional item response theory model to testlet- based tests.(2), 145–168.

Distefano, C., Greer, F. W., & Kamphaus, R. W. (2013). Multifactor modeling of emotional and behavioral risk of preschool-age children.(2), 467–476.

Gignac, G. E. (2008). Higher-order models versus direct hierarchical models: A superordinate or breadth factor?.(1), 21–43.

Gu, H., & Wen, Z. (2017). Reporting and interpreting multidimensional test scores: A bi-factor perspective., 504–512.

[顾红磊, 温忠麟. (2017). 多维测验分数的报告与解释: 基于双因子模型的视角.(4), 504–512.]

Gu, H., Wen, Z., & Fan, X. (2017a). Structural validity of the Machiavellian personality scale: A bifactor exploratory structural equation modeling approach., 116–123.

Gu, H., Wen, Z., & Fan, X. (2017b). Examining and controlling for wording effect in a self-report measure: A Monte Carlo simulation study.(4), 545–555.

Gustafsson, J. E., & Balke, G., (1993). General and specific abilities as predictors of school achievement.(4), 407–434.

Hau, K. T., Wen, Z., Cheng, Z. (2004).. Beijing, China: Educational Science Publishing House.

[侯杰泰, 温忠麟, 成子娟. (2004).. 北京：教育科学出版社.]

Hoogland, J. J., & Boomsma, A. (1998). Robustness studies in covariance structure modeling: An overview and a meta- analysis.(3), 329– 368.

Howard, J. L., Gagné, M., Morin, A. J. S., & Forest, J. (2018). Using bifactor exploratory structural equation modeling to test for a continuum structure of motivation..(7), 2638–2664.

Hyland, P., Boduszek, D., Dhingra, K., Shevlin, M., & Egan, A. (2014). A bifactor approach to modelling the Rosenberg Self Esteem Scale., 188–192.

Mackinnon, D. P., Lockwood, C. M., & Williams, J. (2004). Confidence limits for the indirect effect: Distribution of the product and resampling methods.(1), 99–128.

Marsh, H. W., Hau, K. T., & Wen, Z. L. (2004). In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler's (1999) findings.(3), 320–341.

Muthén, L. K., & Muthén, B. O. (2012).(7ed.). Los Angeles, CA: Muthén & Muthén.

Reise, S. P., Scheines, R., Widaman, K. F., & Haviland, M. G. (2013). Multidimensionality and structural coefficient bias in structural equation modeling: A bifactor perspective.(1), 5–26.

Salerno, L., Ingoglia, S., & Coco, G. L. (2017). Competing factor structures of the Rosenberg Self-Esteem Scale (RSES) and its measurement invariance across clinical and non-clinical samples., 13–19.

Schmid, J., & Leiman, J. M. (1957). The development of hierarchical factor solutions.(1), 53–61.

Wang, M. T., Fredricks, J. A., Ye, F., Hofkens, T. L., & Linn, J. S. (2016). The math and science engagement scales: Scale development, validation, and psychometric properties., 16–26.

Wen, Z., Hau, K.T., & Marsh, H.W. (2004). Structural equation model testing: Cutoff criteria for goodness of fit indices and chi-square test.(2), 186– 194.

[温忠麟, 侯杰泰, 马什赫伯特. (2004). 结构方程模型检验:拟合指数与卡方准则.(2), 186–194.]

Wu, Y., Wen, Z., Marsh, H. W., & Hau, K-T., (2013). A comparison of strategies for forming product indicators for unequal numbers of items in structural equation models of latent interactions.(4), 551–567.

Xu, S. X., Yu, Z. H., & Li, Y. M. (2017). Simulated data comparison of the predictive validity between bi-factor and high-order models.(8), 1125– 1136.

[徐霜雪, 俞宗火, 李月梅. (2017). 预测视角下双因子模型与高阶模型的模拟比较.(8), 1125–1136.]

Ye, B., & Wen, Z. (2012) Estimating homogeneity coefficient and its confidence interval.(12), 1687–1694.

[叶宝娟, 温忠麟.(2012). 测验同质性系数及其区间估计.(12), 1687–1694.]

Yung, Y-F., Thissen, D., & Mcleod, L. D. (1999). On the relationship between the higher-order factor model and the hierarchical factor model.(2), 113–128.

附录1

TITLE: Bifactor model

DATA: FILE = p1.dat; !文件名

VARIABLE: NAMES = y1-y3 x1-x12; !变量命名

MODEL:

Y by y1-y3; !Y表示效标变量

S1 by x1-x4*;

S2 by x5-x8*;

S3 by x9-x12*; !S1-S3表示局部因子

G by x1-x12*;！G表示全局因子

G@1; S1-S3@1; G with S1-S3@0; S1-S3 with S1- S3@0;

Y ON G S1-S3;！全局因子和局部因子作为预测变量

OUTPUT: stdyx;

附录2

TITLE: High-order factor model

DATA: FILE = p1.dat; !文件名

VARIABLE: NAMES = y1-y3 x1-x12;!变量命名

MODEL:

Y by y1-y3; !Y表示效标变量

F1 by x1-x4;

F2 by x5-x8;

F3 by x9-x12; !F1-F3表示一阶因子

G by F1-F3*(h1-h3);！G表示高阶因子

G@1; F1-F3@1;

Y ON G*(d)

F1-F3*(c1-c3);！高阶因子和一阶因子作为预测变量

MODEL CONSTRAINT:

NEW (c); ！c为高阶因子和一阶因子的残差作为预测变量时, 高阶因子的结构系数。

c=d+h1*c1+h2*c2+h2*c2;

OUTPUT: stdyx ;

A general simulation comparison of the predictive validity between bifactor and high-order factor models

WEN Zhonglin; TANG Dandan; GU Honglei

(Center for Studies of Psychological Application / School of Psychology, South China Normal University, Guangzhou 510631, China) (School of Education Science, Xinyang Normal University, Xinyang 464000, China)

Mathematically, a high-order factor model is nested within a bifactor model, and the two models are equivalent with a set of proportionality constraints of loadings. In applied studies, they are two alternative models. Using a true model with the proportional constraints to create simulation data (thus both the bifactor model and high-order factor model fitted the true model), Xu, Yu and Li (2017) studied structural coefficients based on bifactor models and high-order factor models by comparing the goodness of fit indexes and the relative bias of the structural coefficient in a simulation study. However, a bifactor model usually doesn’t satisfy the proportionality constraints, and it is very difficult to find a multidimensional construct that is well fitted by a bifactor model with the proportionality constraints. Hence their simulation results couldn’t extend to general situations.

Using a true model with the proportionality constraints (thus both the bifactor model and high-order factor model fitted the true model) and a true model without the proportionality constraints (thus the bifactor model fitted the true model, whereas the high-order factor model fitted a misspecified model), this Monte Carlo study investigated structural coefficients based on bifactor models and high-order factor models for either a latent or manifest variable as the criterion. Experiment factors considered in the simulation design were: (a) the loadings on the general factor, (b) the loadings on the domain specific factors, (c) the magnitude of the structural coefficient, (d) sample size. When the true model without proportionality constraints, only factors (a), (c) and (d) were considered because the loadings on domain specific factors were fixed to different levels (0.4, 0.5, 0.6, 0.7) that assured the model does not satisfy the proportionality constraints.

The main findings were as follows. (1) When the proportionality constraints were held, the high-order factor model was preferred, because it had smaller relative bias of the structural coefficient, and lower type Ⅰ error rates (but also lower statistical power, which was not a problem for a large sample). (2) When the proportionality constraints were not held, however, the bifactor model was better, because it had smaller relative bias of the structural coefficient, and higher statistical power (but also higher type Ⅰ error rates, which was not a problem for a large sample). (3) Bi-factor models fitted the simulation data better than high-order factor models in terms of fit indexes CFI, TLI, RMSEA, and SRMR whether the proportionality constraints were held or not. However, the bifactor models were less fitted according to information indexes (i.e., AIC, ABIC) when the proportionality constraints were held. (4) Whether the criterion was a manifest variable or a latent variable, the results were similar. However, for the manifest criterion variable, the relative bias of the structural coefficient was smaller.

In conclusion, a high-order factor model could be the first choice to predict a criterion under the condition of proportionality constraints or well fitted for the sake of parsimony. Otherwise, a bifactor model is better for studying structural coefficients. The sample size should be large enough (e.g., 500+) no matter which model is employed.

structural coefficient; bifactor model; high-order factor model; proportionality constraints

10.3724/SP.J.1041.2019.00383

2018-06-22

* 国家自然科学基金项目(31771245)资助。

温忠麟, E-mail: wenzl@scnu.edu.cn

B841