风险决策和跨期决策的过程比较：以确定效应和即刻效应为例*

周 蕾 李爱梅 张 磊 李 纾 梁竹苑



风险决策和跨期决策的过程比较：以确定效应和即刻效应为例

周 蕾李爱梅张 磊李 纾梁竹苑

(暨南大学管理学院, 广州 510632) (中国科学院行为科学重点实验室(中国科学院心理研究所), 北京 100101) (中国科学院大学心理学系, 北京 100049) (德国汉堡大学医学院系统神经科学系, 汉堡 20246)

风险决策和跨期决策与人类生存发展密切相关, 且两类决策在理论发展、行为效应及神经基础等方面具有相似性。为检验二者是否具有共同过程机制, 本研究以风险决策中的确定效应和跨期决策中的即刻效应为例, 采用眼动追踪技术比较了它们的局部、整体过程及模型拟合。辅以贝叶斯因子分析实验数据表明：二者的主要过程特征均相似, 且更符合非折扣模型假设; 二者在加工复杂程度等少数特征上有所不同; 确定和即刻信息在加工方向等特征上存在特异性。这表明二者可能具有共同的核心决策规则：两类决策更可能遵循非折扣模型预期的简捷、启发式规则, 而不是折扣模型所假设的补偿性、基于选项规则。本研究为建立两类决策的共同解释框架做出了有益尝试, 并为决策比较研究方法提供新的方向。

风险决策; 跨期决策; 眼动追踪; 分层贝叶斯模型; 确定效应; 即刻效应

1 前言

风险和跨期决策是与人类生存发展密切相关的两类重要决策。风险决策(risky choice)指人们对具有多个结果且其发生概率已知的选项进行权衡后做出的决定(Kahneman & Tversky, 1979), 如选择不同医疗方案。跨期决策(intertemporal choice)指人们对发生在不同时间点的备择方案间进行权衡后做出的决定(Frederick, Loewenstein, & O'Donoghue, 2002), 如减少过度开发以加强环境保护。二者在理论发展、行为效应及神经基础等方面具有相似性, 因此, 探索它们是否具有共同机制, 对发展普适性决策理论、简化决策概念和模型具有重要意义(Green, Myerson, & Vanderveldt, 2014)。但目前这一问题仍存在争议, 缺少基于决策过程的关键证据。但囿于目前研究的两个局限, 即缺少基于决策过程的关键证据以及传统假设检验无法接受虚无假设, 阻碍了我们对这一问题的理解。近年来决策任务过程分析和贝叶斯因子分析技术渐趋于成熟, 尤其是贝叶斯因子分析可以为虚无假设的成立提供证据, 较好弥补传统虚无假设显著性假设检验的缺陷(吴凡, 顾全, 施壮华, 高在峰, 沈模卫, 2018)。因此, 本文适逢其时采用眼动追踪研究对风险和跨期决策进行过程比较, 辅以贝叶斯因子分析, 以期探索并回答风险和跨期决策是否具有共同机制这一科学问题。

1.1 风险和跨期决策的相似性

1.1.1 理论发展

从理论发展看, 两类决策非常相似, 均遵循折扣模型到非折扣模型的路径。尽管这些模型对具体计算规则有不同假设, 但均隐含了一个重要推论：二者具有共同的核心算法。

折扣模型源于无限理性假设, 即个体获得与决策相关的所有信息, 并通过逻辑和统计推理或概率法则等得到最优化结果(optimal outcome) (Stevens, 2011)。这类模型的共性是假设决策遵循补偿性(compensatory)和基于选项(alternative-based)的规则, 即个体需加工选项的所有维度, 对各选项内部信息整合并比较选项效用大小, 从而做出决策(Stevenson, Busemeyer, & Naylor, 1990)：如风险决策经典的期望价值理论(Pascal, 1670)及随后一系列的概率折扣(probability discounting)理论, 如预期理论(prospect theory) (Kahneman & Tversky, 1979)等; 类似地, 跨期决策有经典的折扣效用模型(discounted utility model) (Samuelson, 1937)和据此发展的时间折扣(temporal discounting)模型, 如双曲线模型(hyperbolic discounting model) (Loewenstein & Prelec, 1992)等。

非折扣模型源于诺贝尔经济学奖得主Herbert Simon提出的有限理性(bounded rationality)假设, 即因受到计算能力、时间等因素的限制, 个体进行决策时的理性程度有限(Simon, 1982)。这类模型的共性是假设决策遵循非补偿性(non-compensatory)和基于维度(attribute-based)的决策规则, 即个体只依据有限的维度, 通过对不同维度进行比较进而做出决策(Stevenson et al., 1990)：如风险决策的占优启发式模型(priority heuristic) (Brandstätter, Gigerenzer, & Hertwig, 2006)、齐当别模型(equate- to-differentiate model) (Li, 2004)、跨期决策的权衡模型(tradeoff model) (Scholten & Read, 2010)、漂移扩散模型(drift diffusion model) (Dai & Busemeyer, 2014)等。

1.1.2 风险和跨期决策类比关系的研究

风险和跨期决策在理论上的相似性引起了研究者对二者本质关系的探索, 这些研究多采用基于决策结果(outcome-based)或拟合优度(goodness-of-fit)的方法(Zhou, Zhang, Li, & Liang, 2018), 可概括为三类：第一类研究尝试建立二者的共适性模型。如, Green, Myerson和Ostaszewski (1999)基于折扣模型框架建立了适用于二者的双曲线折扣模型, 并很好地拟合了两类决策。第二类研究旨在发现两类决策中相似的行为效应(周蕾, 2017)。如, 风险决策中存在确定效应(Kahneman & Tversky, 1979)、伪确定效应(Kahneman & Tversky, 1984)、Allais悖论(Allais, 1953)和隐藏零效应(Liang, Zhou & Su, 2016), 与之对应, 跨期决策中存在即刻效应(Kirby & Herrnstein, 1995)、伪即刻效应(Li, Su, & Sun, 2010)、落花悖论(Rao & Li, 2011)和隐藏零效应(Magen, Dweck, & Gross, 2008)。第三类研究考察概率或时间对两类决策的交互作用, 探索二者是否对另一类决策具有同等影响(Hardisty & Pfeffer, 2016; Luckman, Donkin, & Newell, 2017)。如, Weber和Chapman (2005)发现, 在风险决策中增加“时间”变量, 或在跨期决策中增加“概率”变量, 将消除确定效应和即刻效应, 揭示出两类决策可能等价。

此外, 两类决策可能存在相似甚至部分共同的神经基础。例如, 研究发现, 风险决策中, 不同脑区的激活可预测不同的行为模式, 如伏隔核激活预测风险寻求, 而前脑岛激活预测风险规避(Kuhnen & Knutson, 2005)。类似地, 跨期决策中, 人们或通过单一/分离的神经系统评估选项的价值并做出决策(Kable & Glimcher, 2007; McClure, Laibson, Loewenstein, & Cohen, 2004), 或通过自我控制脑区的作用产生偏好不一致(Figner et al., 2010)。更有少量研究揭示, 两类决策均与认知执行控制相关脑区(Weber & Huettel, 2008), 以及认知和情感相关脑区(吴燕, 周晓林, 罗悦嘉, 2010)密切关联。

1.1.3 确定效应和即刻效应

在两类决策相似的行为效应中, 最为经典的是确定效应和即刻效应。风险决策中人们经常会发生如下的偏好反转(Kahneman & Tversky, 1979)：在决策1中偏好确定选项A; 但当两个选项等比例变化为决策2时, 更偏好风险选项B’。这就是确定效应。

决策1：A. 100%的概率得30美元; B. 80%的概率得45美元;

决策2：A’. 25%的概率得30美元; B’. 20%的概率得45美元;

类似地, 跨期决策中人们会在决策3中偏好即刻选项A; 但在等比例变化的决策4中更偏好延迟选项B’ (Kirby & Herrnstein, 1995)。这就是即刻效应。

决策3：A. 现在得30美元; B. 1年后得45美元;

决策4：A’. 1年后得30美元; B’. 2年后得45美元;

这两种效应被广泛研究且非常稳定。在风险决策中, 使用多种方法设置不同任务和情境, 均发现确定效应(Schneider, Streicher, Lermer, Sachs, & Frey, 2017)。而在跨期决策中, 多数研究者认为即刻效应是其偏好动态不一致性的根源(Read, Loewenstein, & Kalyanaraman, 1999)。可见, 此对效应的决策过程可能更不易受研究方法干扰。

有趣的是, 此对效应也存在类似的解释机制：个体对确定和即刻选项赋予了过高权重(Kahneman & Tversky, 1979; Kirby & Herrnstein, 1995)。这暗示着不同于其他取值点, 当概率和时间延迟信息在其端点取值(概率为“100%”或时间为“现在”)时, 确定和即刻信息可能具有较强的对应关系, 并通过类似的机制对人们的行为偏好产生影响。

综上可见, 两类决策可能具有共同的效应机制。但前人采用基于结果的方法难以检验潜在认知过程(Schulte-Mecklenbeck et al., 2017)。因此, 可能需要从决策过程的角度更准确地揭示二者的关系。

1.2 决策过程：风险和跨期决策的眼动研究

基于决策过程的研究可克服基于结果研究方法的局限, 为决策的信息输入和输出间的关联提供更直接客观的重要证据(Schulte-Mecklenbeck et al., 2017)。其中, 因数据的信息量大, 能同时反映时间和空间特征, 眼动追踪技术被广泛应用于决策的过程研究(魏子晗, 李兴珊, 2015)。

风险决策的眼动研究主要集中在模型检验和考察眼动过程与选择偏好关系的角度。如, 李纾及其同事通过分析加工方向等特征, 发现风险决策的主要加工过程具有非补偿、基于维度的特征, 并不支持折扣模型(Su et al., 2013; 汪祚军, 李纾, 2012; Zhou et al., 2016)。Glöckner等却发现, 风险决策更符合基于补偿性规则的平行强制满足模型(parallel constraint satisfaction models, PCS) (Fiedler & Glöckner 2012; Glöckner & Herbold, 2011)。还有研究揭示注视转换及最后注视选项等特征可有效预测选择结果(Brandstätter & Körner, 2014; Stewart, Hermens, & Matthews, 2015)。

跨期决策的眼动研究相对较少, 主要考察过程特征与选择偏好的因果关系。如发现时间折扣率大的个体对即刻选项存在注意偏差, 且这种偏好可预测冲动性行为(Franco-Watkins, Mattson, & Jackson., 2016)。因此, 通过操纵注意偏好(Fisher & Rangel, 2013)或搜索策略(Reeck, Wall, & Johnson, 2017), 可促使人们选择大而远的选项。但检验跨期决策模型的眼动研究尚为罕见。

1.3 问题提出

综上所述, 探索风险和跨期决策的相似性有助于认识二者的共同特征, 并发展二者的普适性理论。然而, 目前的研究现状阻碍了我们对这个问题的认识：

首先, 两类决策经典的折扣模型假设二者具有相似的加工过程, 但现有的研究大多使用基于结果的方法, 若非从过程的角度揭示二者相似性的内在机制, 其基于结果的证据不足以令人信服。

其次, 已有的眼动研究在分析方法和指标选择上存在不足。两类决策的经典模型大多暗含着信息搜索与评价的动态序列过程(Kahneman & Tversky, 1979), 因此, 从整体、动态的视角去考察二者的时间序列属性十分必要。然而, 已有研究较少选取反应整体过程特征的指标, 更鲜有研究系统地采用基于局部、整体过程等多方面特征。

最后, 以往研究在建立二者共适性模型时, 其算法选择存在不足。前人多基于最大似然估计(Maximum likelihood estimation, MLE), 独立地对个体进行模型估计(Green et al., 1999; Green et al., 2014), 丧失了总体层面的共性; 且MLE未考虑个体间的相关性, 导致模型参数可能充满噪音且不稳定(Scheibehenne & Pachur, 2015), 此缺陷在常见的小样本决策研究中更为明显。

1.4 研究目的与假设

为克服以上不足, 本研究采用眼动追踪技术, 以确定效应和即刻效应为例, 通过匹配的实验范式比较两类决策, 探索“二者加工过程是否相似”及“该过程更符合哪一类模型的假设”。

本研究假设二者具有相似的行为和过程特征。鉴于新近的模型更多基于非折扣模型框架(Scholten & Read, 2010; Dai & Busemeyer, 2014), 亦有大量支持非折扣模型的过程证据(Fisher & Rangel, 2013; Su et al., 2013), 我们亦假设二者均更符合非折扣模型。

本研究基于行为、局部和整体过程特征及模型拟合多个层面, 选取可区分模型的关键过程规则进行比较。规则1：补偿性/非补偿性, 即决策依据所有信息或部分信息, 以及是否包含审慎加工的复杂计算过程; 规则2：基于选项/基于维度, 即决策过程是在选项内或选项间进行(Stevenson et al., 1990)。本研究选择了不同眼动属性作为检验上述规则中局部过程特征的指标：加工复杂程度和加工深度检验“补偿性/非补偿性”规则, 加工方向检验“基于维度/基于选项”规则; 选取眼动轨迹为检验决策的整体过程特征的指标; 并利用分层贝叶斯模型拟合(hierarchical Bayesian modeling, HBM)的方法, 对不同备择决策模型进行拟合。

具体假设如下。

行为特征：

H(反应时)：二者决策时间无显著差异。

H(选择偏好)：风险决策存在确定效应, 跨期决策存在即刻效应。

局部过程特征：

H(加工复杂程度)：二者加工复杂程度无显著差异。

H(加工深度)：二者在决策前注视信息量百分比无显著差异。

H(加工深度)：二者在决策前均无需注视所有选项特征。

H(加工方向)：二者基于选项的眼跳和基于维度眼跳的频数分布无显著差异。

整体过程特征：

H：二者眼动轨迹无显著差异。

模型拟合：

H：相对于折扣模型, 二者能更好地被非折扣模型拟合。

2 方法

2.1 被试

来自中国科学院大学、北京林业大学等高校学生33名(= 26.72岁,= 2.18岁;= 17), 均为右利手, 无红绿色盲, 视力或矫正视力正常, 实验前均签署了知情同意书。

每个被试可获得30元基本报酬和5~10元的奖励报酬。

2.2 仪器

采用由SR Research公司开发的Eye Link 2000型眼动仪, 采样率为2000 Hz, 记录注视点最短时长40 ms。实验中采用距离显示器58 cm的腮托, 利用眼动追踪系统的自动补偿机制, 使得头动对眼动轨迹记录的影响达到最小。实验刺激呈现于19英寸、分辨率为1024×768的TCL纯平显示器上。被试眼睛与屏幕边缘的水平视角为28, 垂直视角为21。被试通过微软SideWinder游戏手柄的按键来完成反应。

2.3 实验材料和流程

本研究采用2(任务：风险/跨期)×2(是否包含确定/即刻选项：包含/不含)被试内设计。被试需要先后完成风险和跨期决策任务(顺序随机), 通过按键选择更偏好的选项。在风险任务中, 被试在发生概率不同的两个选项中选择：大概率获得一笔小数量的钱(“smaller-outcome, larger-probability”, 简称SL选项), 或小概率获得一笔大数量的钱(“larger-outcome, smaller-probability”, 简称LS选项)。其中, 包含确定选项条件下, 每个试次包含确定选项A和风险选项B。确定选项的结果(报酬)为300元或700元, 其EV (expected value)值略小于风险选项EV值(Kahneman & Tversky, 1979); 不含确定选项条件的材料由确定选项条件变换构成：该条件中各选项的概率为确定条件中两个选项的获得概率乘以小于1的比例而来, 各选项的结果不变。

类似地, 在跨期任务中, 被试在获得时间不同的两个选项中选择：在较近的将来获得一笔小数量的钱(“smaller-outcome, sooner”, 简称SS选项), 或在较远的将来获得一笔大数量的钱(“larger-outcome, later”, 简称LL选项)。其中, 在包含即刻选项条件, 每个试次包含即刻选项A和延迟选项B, 选项结果(报酬)和风险决策任务相等; 不含即刻选项条件的材料由即刻选项条件的材料变换构成：该条件的获得时间为即刻选项条件中各选项的获得时间加上一定的时间, 各选项的结果不变。

任务流程如图1所示。任务开始前, 被试阅读指导语并完成4次练习, 以熟悉任务要求。每个任务包含32个试次, 分为2个组块。组块间休息至少1分钟, 任务间休息至少2分钟。为确保被试每次注视不能(通过余光)同时获取多余一处信息(如报酬数额、支付时间等), 刺激中所有信息均呈现于其他相邻信息的边缘区域, 即距离其他相邻信息中央5视角外区域(Rayner, 2013)。

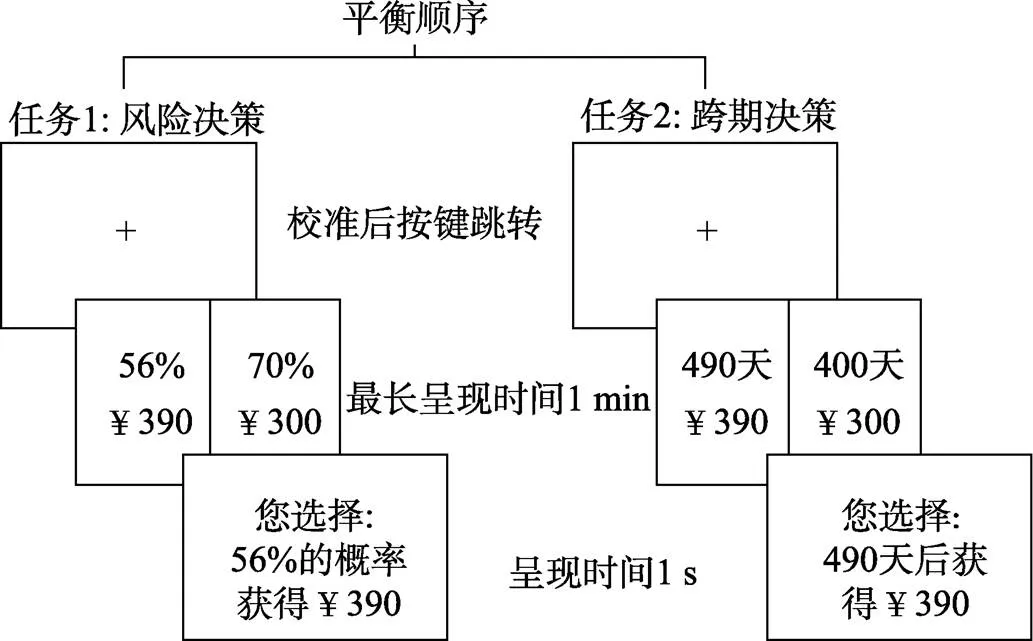
图1 实验流程示意图

所有任务结束后, 在每个任务中随机选取一个试次, 以被试的实际选择(按照一定的比例)作为实验报酬的一部分。其中, 在风险任务中, 若被试选择风险选项, 计算机将运行一个相应概率和结果的博彩程序, 被试以实际反馈的奖励获得报酬。在跨期任务中, 被试将依据实际选择, 在对应的时间获得报酬。

2.4 数据分析方法

研究所检验的决策属性及分析指标和方法等见图2。

2.4.1 局部过程特征比较

加工复杂程度：用单个注视点平均时长测量。注视点时长是反映加工水平的可靠指标, 随着任务难度的增加, 注视点时长也越长(Horstmann, 2009)。如果决策采取了补偿性规则, 则可能包含审慎的计算过程, 注视点的平均时长应相对较长; 反之, 则可能不是基于补偿性规则。此外, 本研究也计算了长注视点在决策过程中所占比例作为补充。

加工深度：用决策前注视的选项特征数量测量(Su et al., 2013)。如果个体依据补偿性规则加工, 决策前应加工所有的选项特征; 反之, 则更可能依据非补偿性规则加工。

加工方向：用SM值(alternative-based vs. dimension- based searched measure) (Böckenholt & Hynan, 1994)度量基于选项和基于维度眼跳的分布, 其计算公式如下：

其中, A和D分别代表选项和维度数量(A = 2, D = 2); r和r分别代表基于选项和基于维度眼跳的频次, N代表眼跳的总频次。SM值为0, 代表并不存在具有优势的眼跳模式; 与0相比, SM值越大, 代表个体主要的加工模式是基于选项, 反之则更基于维度加工。

SM值服从标准正态分布, 已被广泛应用于决策的眼动研究(Konstantinidis, van Ravenzwaaij, & Newell, 2017; Schulte-Mecklenbeck, Kühberger, Gagl, & Hutzler, 2017; Su et al., 2013)。以SM值为搜索模式的测量指标适用于检验基于选项和维度的决策模型：操纵选项和维度数量时, 其均值稳定, 得到极端数值的概率极低(Böckenholt & Hynan, 1994)。相对于其他指标, 它对搜索模式的变化更敏感：如操纵搜索策略, 使占优的搜索模式切换, SM值可敏感地探测出这种变化(Böckenholt & Hynan, 1994)。因此, 在本研究中, 如果个体依据补偿性规则加工, 其决策的主要加工方向是基于选项, SM值应相对较大; 反之, 更可能是基于维度加工。

2.4.2 整体过程特征比较

本研究选取眼动轨迹对决策的整体过程进行比较。眼动轨迹由个体内化的认知模型驱动, 以一种自上而下的认知加工方式形成, 反映大脑对视觉刺激加工顺序和整体动态的眼动模式 (Noton & Stark, 1971)。为直观地观察不同任务典型的眼动轨迹模式, 本研究使用了Zhou等人(2016)的方法定义了典型试次(typical trial)眼动轨迹。典型试次是各实验条件下, 与其他试次的平均相似程度最大(平均数)、最具有代表性的试次。因此, 某任务的典型试次轨迹即该任务中最具有代表性的眼动轨迹模式,当该任务内眼动轨迹相似性呈正态分布时, 也是该任务条件内的平均眼动轨迹。

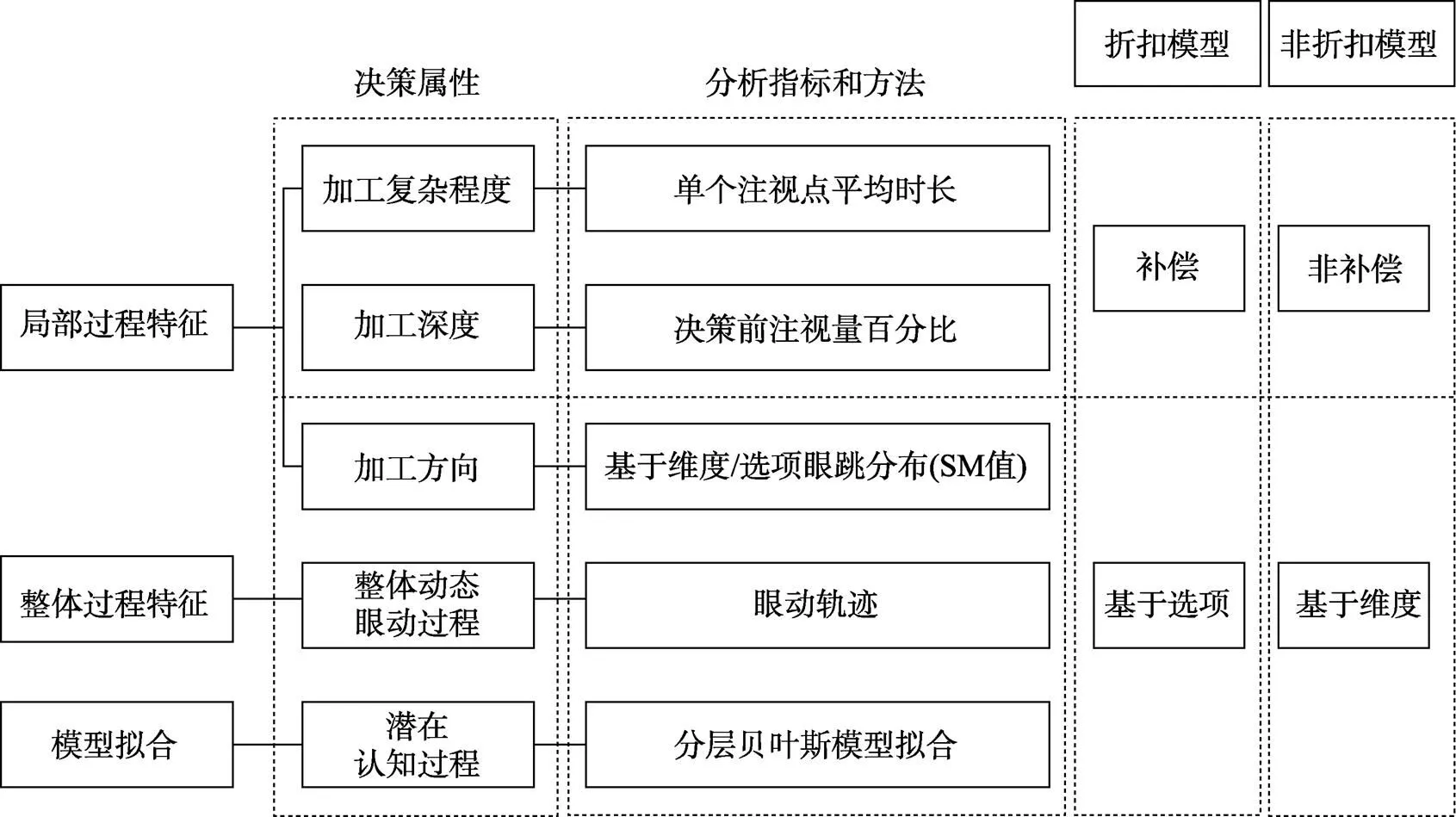
图2 研究逻辑与分析框架

典型试次的计算步骤如下：1) 基于各个条件, 计算所有试次和其他试次的相似性分数; 2) 计算每个试次和其他试次相似性分数的平均数; 3) 选择各条件下, 与其他试次平均相似性分数最大的试次, 将该试次定义为所属条件的典型试次。因此, 在本研究中, 如果1) 风险和跨期决策任务眼动轨迹的条件内相似性分数与条件间相似性分数无显著差异, 则说明二者的整体加工过程相似, 反之, 则不相似; 2) 如果某任务的典型试次具有折扣模型所假设的加工过程, 则可以定性地判断决策可能依据补偿性、基于选项规则, 反之, 则不符合折扣模型的假设。

2.4.3 模型拟合的比较

为回答风险与跨期决策的过程更符合哪种理论模型, 本研究利用分层贝叶斯模型拟合(Hierarchical Bayesian Modeling, HBM)方法, 对不同备择决策模型进行拟合。与最大似然估计(MLE)相比, HBM方法的优势在于(Gelman et al., 2014; Ahn, Haines, & Zhang, 2017)：HBM采用分层模型, 通过引入群体水平参数(group-level parameters)对个体层面参数(individual-level parameters)进行调控, 基于观测数据同时估计群体和个体水平的参数, 使得模型拟合更加高效、稳定和可靠; MLE多进行点估计(point estimate), HBM使用MCMC (Markov chain Monte Carlo)算法对参数最可能存在的分布形态进行取样逼近, 从而得到模型参数的后验分布(posterior distribution), 可以提供更多信息。这两点优势对样本较小的实验室研究尤为有效。最后, 基于贝叶斯原理, 该方法可计算参数后验分布的差异, 以便进行组间比较(Scheibehenne & Pachur, 2015; Ahn et al., 2017)。

分层贝叶斯模型拟合使用了R软件包hBayesDM (hierarchical Bayesian modeling of Decision-Making tasks) (Ahn et al., 2017)。所有模型拟合均使用4条独立的MCMC链, 每条链包含1000个有效样本, 因此所有参数的后验分布均由4000个有效样本组成。Gelman-Rubin 检验(Gelman & Rubin, 1992)表明所有参数的R̂均小于1.1, 表明四条独立的MCMC达到聚拢, 模型拟合的结果稳定可靠。我们采用WAIC (widely applicable information criterion) (Vehtari, Gelman, & Gabry., 2015)作为贝叶斯模型比较的依据。WAIC使用所有MCMC后验样本计算模型的样本外预测性(out-of-sample predictive accuracy)。为避免过度拟合(overfitting), 在模型比较中对参数数量做了惩罚(penalize), 兼顾了模型的复杂程度。WAIC值越小表明模型的样本外预测性(out of-sample predictive accuracy)越强, ∆WAIC > 10即可认为有显著差异(Burnham & Anderson, 2004)。

WAIC的计算公式如下：

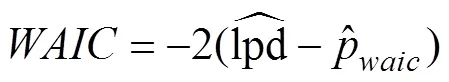
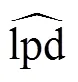
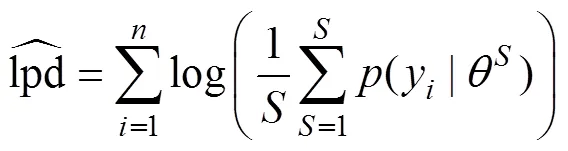
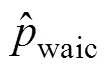
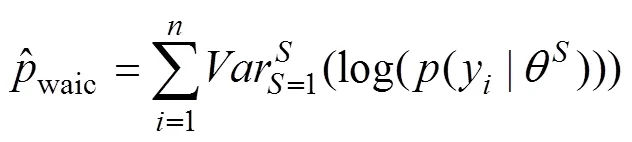
研究选取三个理论模型对风险和跨期决策任务进行了模型拟合和参数估计。其中, 经典折扣模型选择了指数模型(exponential model, 模型1) (Samuelson, 1937)和双曲线模型(hyperbolic model, 模型2) (Mazur, 1987), 二者的核心假设是：个体按照基于选项规则进行决策, 计算折扣率并选择主观效用大的选项。

非折扣模型选择了跨期决策启发式模型(inter-temporal choice heuristic, ITCH, 模型3) (Ericson, White, Laibson, & Cohen, 2015), 其核心假设是：个体按照一系列基于维度比较的规则组合而成的启发式策略进行决策, 赋予不同的规则以不同权重, 并根据这些规则选出更优的选项。该模型的提出是基于心理规则而非经济学理论, 可用于检验基于维度加工规则, 且在不同的任务条件下, 模型参数相对稳定, 受参数情境和实验操纵的影响较小。此外, 与DRIFT启发式模型(Read, Frederick, & Scholten, 2013)和权衡模型(trade-off model) (Scholten & Read, 2010)相比, 对个体的行为结果具有略高的解释力(Ericson et al., 2015)。

各理论模型公式如下：

V = A * e(5)

/ (1 +) (6)

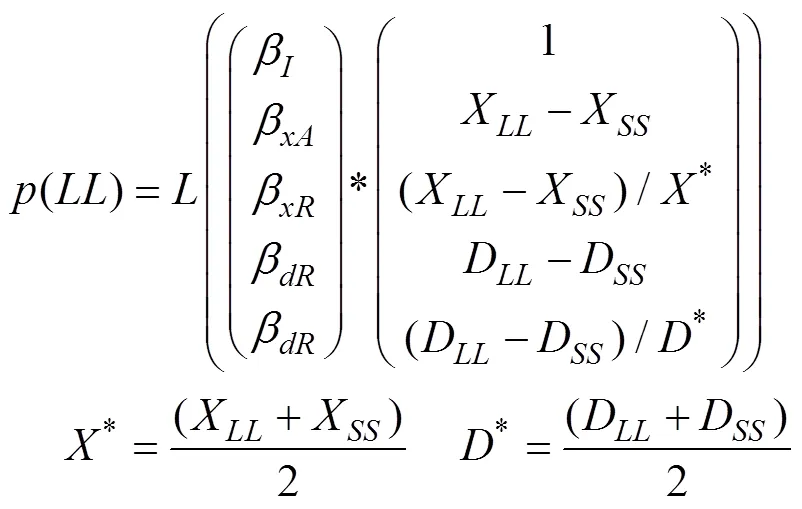
以跨期决策为例, 模型1(公式5)和模型2(公式6)中,代表个体对选项的主观效用(subjective utility),代表将来选项的结果,代表自然对数的底,代表延迟时间,代表折扣率; 模型3(公式7)中,X代表大而远(LL)选项的结果,X代表小而近(SS)选项的结果,D代表大而远(LL)选项的时间,D代表小而近(SS)选项的时间,是一系列自由参数, 代表回归方程中所有项的权重。

通过分析各个决策任务内各个模型拟合指数的优劣, 可判断两类任务是否能被同一种模型更好地拟合。如果折扣模型对任务的拟合程度优于非折扣模型, 说明两类决策更符合折扣模型假设; 反之, 则更符合非折扣模型。

3 结果

眼动数据通过Eyelink Data Viewer (SR Research,加拿大)导出和预处理。眼跳定义为速度超过30/s且加速度超过8000°/s的一次眼动; 注视则定义为两次眼跳之间眼睛位置相对稳定的一段时间。每个刺激材料被划分出4个互不重叠且面积相同(200 × 180像素)的矩形兴趣区, 覆盖了2个选项所有的属性。

本研究中共有2112个正式试次。数据分析时剔除36个试次(1.56%), 其中眼动追踪错误的试次19个(0.90%), 反应时过短(< 200 ms)或过长(大于平均反应时3个标准差)的试次17个(0.79%)。有效试次2076个。此外, 在眼动轨迹分析中共采集到18720个注视点, 由于时长低于50 ms或位于兴趣区以外, 在后续分析中剔除936个(约5.00%)注视点, 有效注视点共17784个。

针对研究问题的独特性, 为了检验两类决策过程是否相同, 即接受“虚无假设”, 在数据分析中, 除了进行传统的假设检验外, 本文采用了贝叶斯因子(Bayes factor)分析。贝叶斯因子分析的优势在于可同时考虑H和H, 基于实验数据对两个假设为真的先验概率进行更新, 以比较哪个理论模型(H和H)更合理(胡传鹏, 孔祥祯, Wagenmakers, Ly, 彭凯平, 2018)。这弥补了传统假设检验的局限, 即无法接受虚无假设, 忽视了H的可能性比H大的情况。因此, 计算贝叶斯因子大小就可以判断在多大程度上可以接受虚无假设。研究采用JASP软件进行贝叶斯因子分析(https://jasp-stats.org/, JASP team 2017) (JASP Team, 2017; Marsman & Wagenmakers, 2017; Wagenmakers et al., 2018a; Wagenmakers et al., 2018b)。其中, 先验分布采用了γ≈0.707柯西(Cauchy)分布(Jeffreys, 1961; Ly, Verhagen, & Wagenmakers, 2016a, 2016b; Rouder, Speckman, Sun, Morey, & Iverson, 2009; 胡传鹏等, 2018)。

3.1 行为特征

3.1.1 决策时间

对反应时进行2(任务：风险/跨期)×2(是否包含确定/即刻选项：包含/不含)重复测量方差分析(ANOVA)发现(图3)：风险任务的决策时间(= 2.81 s,= 0.92)短于跨期任务(= 3.24 s,= 1.09),(1, 32) = 4.62,= 0.04, η=.13, 95% CI [−0.83, −0.02]; 不含确定/即刻选项条件的决策时间(= 3.65 s,= 0.92 s)长于包含确定/即刻选项的条件(= 2.40 s,= 0.80 s),(1, 32) = 108.69,< 0.001, η= 0.77, 95% CI [1.01, 1.50]。简单效应检验显示(交互作用：(1, 32) = 9.86,0.004, η= 0.24), 在不含确定/即刻选项的条件下, 风险任务的反应时(= 3.26 s,= 5.28 s)显著短于跨期任务(= 4.04 s,= 7.76 s),(1, 32)= 11.51,= 0.002; 但在包含确定/即刻选项条件下, 风险任务的反应时(= 2.36 s,= 5.63 s)与跨期任务(= 2.43 s,= 6.26 s)无显著差异,(1, 32)= 0.09,= 0.77。贝叶斯因子分析结果表明, 贝叶斯因子为BF= 5.15, 说明在(假定没有效应的)零假设下出现当前数据的可能性是在(假定存在效应的)备择假设下可能性的5.15倍。根据Jeffreys (1961)提出的分类标准, 这是中等强度的证据支持接受零假设H,即在包含确定/即刻选项条件下, 两类决策时间无显著差异。总之, 决策时间的结果部分支持H。

3.1.2 选择偏好

研究分别以选择SL选项(即“大概率获得小数量钱”), 和SS选项(即“较近将来获得小数量钱”)的比例为因变量进行配对样本检验。在风险任务中, 人们在包含确定选项条件下, 选择SL选项的比例(= 0.83,= 0.28)高于不含确定选项条件(= 0.56,= 0.17),(32) = −5.17,0.01, Cohen’s= −0.90, 95% CI [−0.38, −0.17]。类似地, 在跨期任务中, 人们在包含即刻选项条件下, 选择SS选项的比例(= 0.68,= 0.34)高于不含即刻选项条件(= 0.34,= 0.23),(32) = −6.74,0. 001, Cohen’s−1.17, 95% CI [−0.45, −0.24]。该结果表明, 在行为层面, 重复出了确定效应和即刻效应, 支持H。

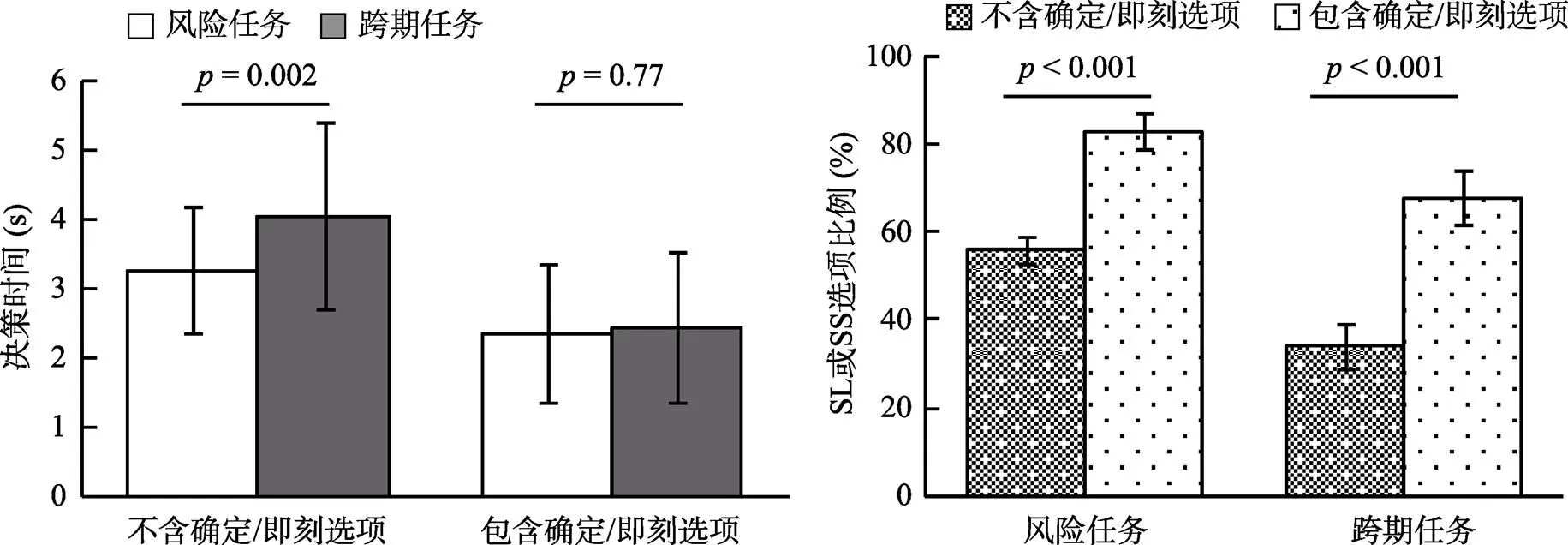
图3 行为特征比较结果(M ± SE)

3.2 局部过程特征

3.2.1 加工复杂程度

以单个注视点平均时长为因变量, 两因素(任务×是否包含确定/即刻选项)重复测量方差分析发现(图4), 两任务的单个注视点平均时长无差异,(1, 32) = 0.63,= 0.43, 95% CI [−13.23, 5.82]; 不含确定/即刻选项条件的单个注视点平均时长(= 224.64 ms,= 33.61 ms)高于包含确定/即刻选项条件(= 208.33 ms,= 34.01 ms),(1, 32) = 19.76,< 0.001, η= 0.38, 95% CI [8.84, 23.79]。简单效应检验结果显示(交互作用：(1, 32) = 5.63,= 0.02, η= 0.15), 不含确定/即刻选项时, 风险任务的单个注视点平均时长(= 218.73 ms,= 40.21 ms)显著短于跨期任务(= 230.55 ms,= 32.97 ms),(1, 32) = 5.19,= 0.03, η= 0.14; 包含确定/即刻选项条件时, 风险任务的单个注视点平均时长(= 210.53 ms,= 45.73 ms)与跨期任务(= 206.13 ms,= 29.81 ms)无显著差异,(1, 32) = 0.48,= 0.49。贝叶斯因子分析发现贝叶斯因子BF= 4.29, 说明在零假设出现当前数据的可能性是在备择假设下可能性的4.29倍, 有中等强度的证据支持接受零假设H(Jeffreys, 1961), 即在包含确定/即刻选项条件下, 风险和跨期任务的单个注视点平均时长无显著差异。总之, 结果部分接受H。作为补充, 以时长超过300 ms的注视点为长注视点(Rayner, 2013), 对其比例进行分析, 结果与单个注视点平均时长类似, 且揭示出两种任务加工过程均更符合非补偿性规则。

3.2.2 加工深度

以决策前注视的选项特征占所有选项特征的百分比(以下简称：注视量百分比)为因变量, 两因素(任务×是否包含确定/即刻选项)重复测量方差分析发现(图5), 风险任务的注视量百分比(= 93.10%,= 8.04%)和跨期任务的注视量百分比(= 94.20%,=7.47%)无显著差异,(1, 32) = 0.57,= 0.46, 95% CI [−0.04, 0.20]; 不含确定/即刻选项条件下, 注视量百分比(= 97.50%,= 0.70%)显著高于包含确定/即刻选项条件(= 89.70%,=9.77%),(1, 32) = 30.10,< 0.001, η= 0.49, 95% CI [ 0.05, 0.11]。简单效应检验结果显示(交互作用：((1, 32) = 0.56,= 0.46), 不包含确定/即刻选项时, 风险任务的注视量百分比(= 96.48%,= 6.32%)与跨期任务(= 98.58%,= 2.88%)的差异边缘显著,(1, 32) = 3.99,= 0.054; 但在包含确定/即刻选项时, 风险任务的注视量百分比(= 89.63%,= 11.36%)与跨期任务(= 89.87%,= 13.40%)无显著差异,(1, 32) = 0.008,= 0.93。贝叶斯因子分析发现贝叶斯因子BF= 5.35, 说明在零假设出现当前数据的可能性是在备择假设下可能性的5.35倍, 有中等强度的证据支持接受零假设H(Jeffreys, 1961), 即在包含确定/即刻选项条件下, 风险和跨期任务的注视量百分比无显著差异。总之, 结果支持假设H。

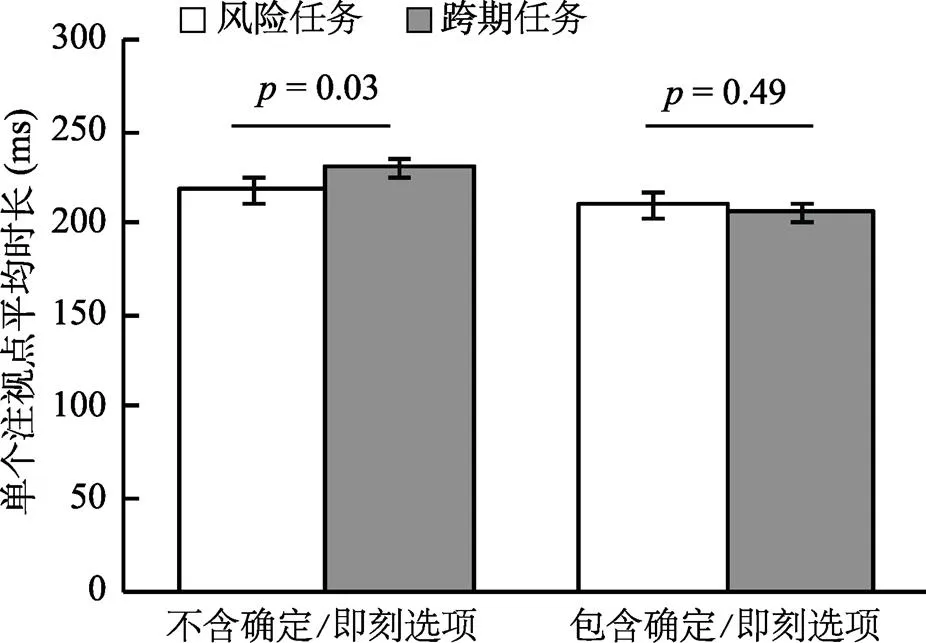
图4 加工复杂程度过程特征比较结果(M ± SE)

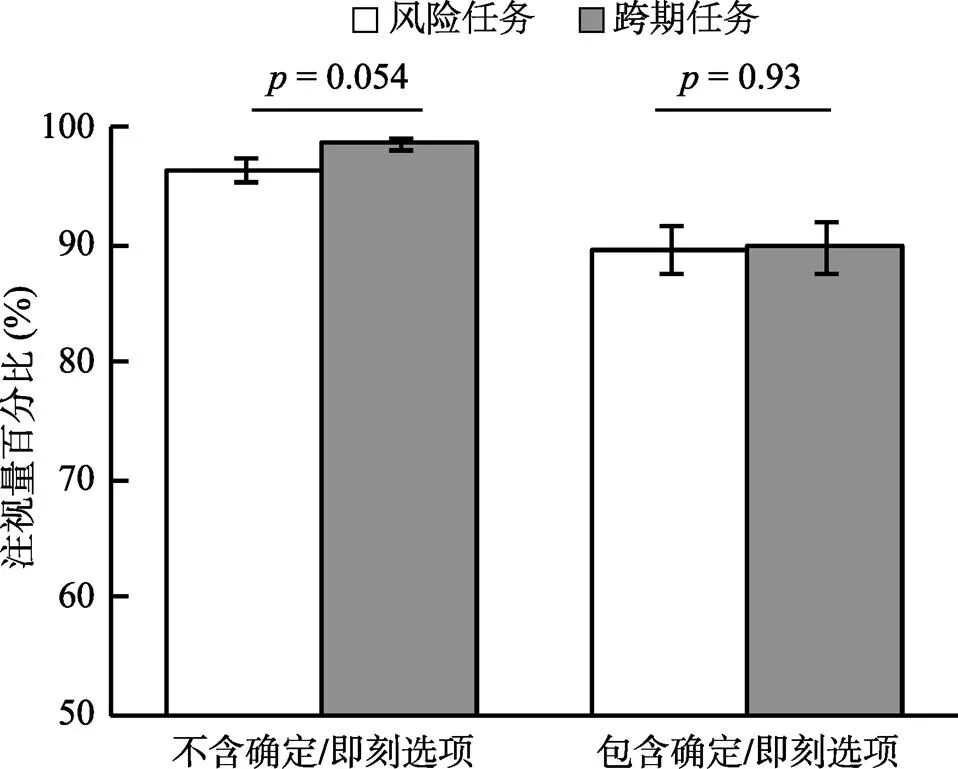
图5 加工深度过程特征比较结果(M ± SE)

研究分别对风险和跨期任务的注视量百分比与100%进行单样本检验(单尾), 发现在风险和跨期任务中, 注视量百分比均显著低于100% ((32) = −5.00,< 0.001, Cohen’s= −0.87;(32) = −4.45,< 0.001, Cohen’s= −0.77)。说明两种任务过程均更符合非补偿性加工的假设, 支持H。

3.2.3 加工方向

对SM值的重复测量方差分析表明(图6), 风险任务SM值的均值(= −0.09,= 0.63)与跨期任务SM值的均值(= −0.27,= 0.69)无显著差异,(1, 32) = 1.36,= 0.25, 95% CI [−0.14, 0.52]; 不含确定/即刻条件的SM值(= −0.42,= 0.52)显著低于包含确定/即刻条件(= 0.06,= 0.52),(1, 32) = 67.61,< 0.001, η= 0.68, 95% CI [−0.59, −0.36])。简单效应检验结果显示(交互作用：((1, 32) = 8.79,= 0.01, η= 0.22), 在不含确定/即刻选项条件下, 风险任务的SM值的均值(= −0.23,= 0.69)与跨期任务SM值的均值(= −0.60,= 0.84)差异边缘显著,(1, 32) = 3.41,= 0.07。贝叶斯因子分析发现贝叶斯因子BF= 1.18, 在零假设出现当前数据的可能性是在备择假设下可能性的1.18倍, 有较弱强度的证据支持接受零假设H(Jeffreys, 1961)。包含确定/即刻选项条件下, 风险任务的SM值的均值(= 0.06,= 0.64)与跨期任务SM值的均值(= 0.05,= 0.57)无显著差异,(1, 32) = 0.001,= 0.98。贝叶斯因子分析发现贝叶斯因子BF= 5.37, 说明在零假设出现当前数据的可能性是在备择假设下可能性的5.37倍, 中等强度的证据支持接受零假设(Jeffreys, 1961), 即在包含确定/即刻选项条件下, 风险和跨期任务的SM值无显著差异。以上结果说明, 风险和跨期任务在加工方向上类似, 部分支持H。

进一步地, 分别对两个条件下的风险和跨期任务的SM值与0进行单样本检验(单尾), 包含确定选项时, 风险任务的SM值与0无显著差异,(32) = 0.92,= 0.30。贝叶斯因子分析发现贝叶斯因子BF= 4.74, 在零假设出现当前数据的可能性是在备择假设下可能性的4.74倍, 有中等强度的证据支持接受零假设H(Jeffreys, 1961), 即风险任务中无优势眼跳模式; 包含即刻选项时, 跨期任务的SM值与0无显著差异,(32) = 0.92,= 0.29, 贝叶斯因子分析发现贝叶斯因子BF= 4.67, 在零假设出现当前数据的可能性是在备择假设下可能性的4.67倍, 中等强度的证据支持接受零假设(Jeffreys, 1961), 即跨期任务中无优势眼跳模式。不含确定/即刻选项时, 风险任务和跨期任务的SM值均显著小于0 (t(32) = −1.90,= 0.03, Cohen’s= −0.33;t(32) = −4.12,< 0.001, Cohen’s= −0.71)。以上结果说明在包含确定/即刻选项时, 风险和跨期任务无优势眼跳, 在不包含确定/即刻选项时, 风险和跨期任务都更基于维度加工。

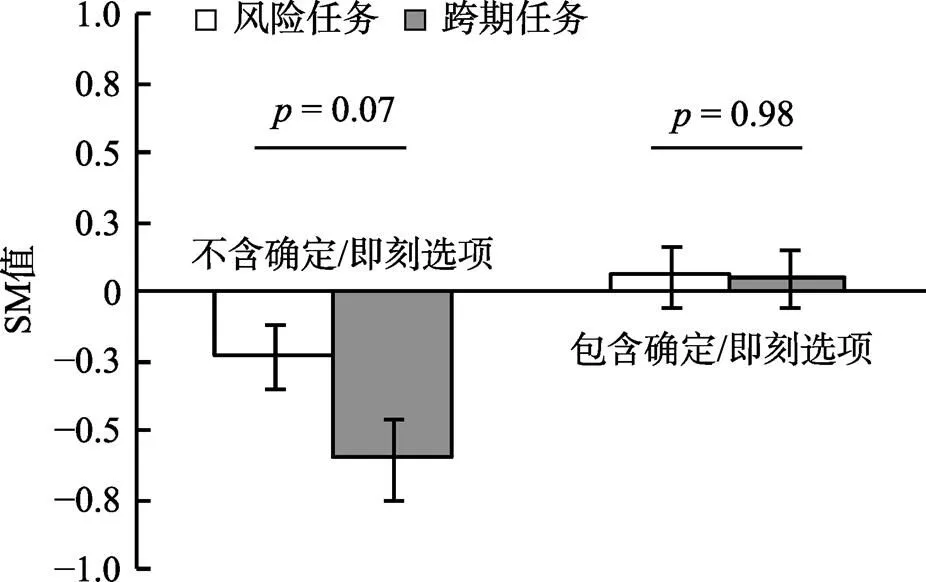
图6 加工方向过程特征比较结果(M ± SE)

3.3 整体过程特征

以眼动轨迹的相似性分数为因变量, 分别在不含/包含确定或即刻选项条件下进行单因素重复测量方差分析(ANOVA)。结果发现(图7), 在不含确定/即刻选项条件下, 风险和跨期决策任务内与任务间眼动轨迹相似性得分差异显著,(1, 32)= 16.82,< 0.001, η= 0.35, 95% CI [0.45, 0.49]。事后比较(Tukey HSD法)显示, 两任务间的眼动轨迹相似性分数(= 0.44,= 0.06)均显著低于风险决策任务内(= 0.50,= 0.05,< 0.001)和跨期决策任务内(= 0.47,= 0.07,= 0.007)。包含确定/即刻选项条件下, 两任务内与任务间眼动轨迹相似性差异显著,(1, 32) = 10.58,< 0.001, η= 0.24, 95% CI [0.47, 0.49]。事后比较(Tukey HSD)显示, 两任务间的眼动轨迹相似性(= 0.46,= 0.05)均显著低于风险决策任务内(= 0.50,= 0.03,= 0.001)和跨期决策任务内(= 0.48,= 0.06,= 0.01)。这一结果拒绝了H, 说明风险和跨期决策眼动轨迹, 即二者整体动态过程特征不相似。

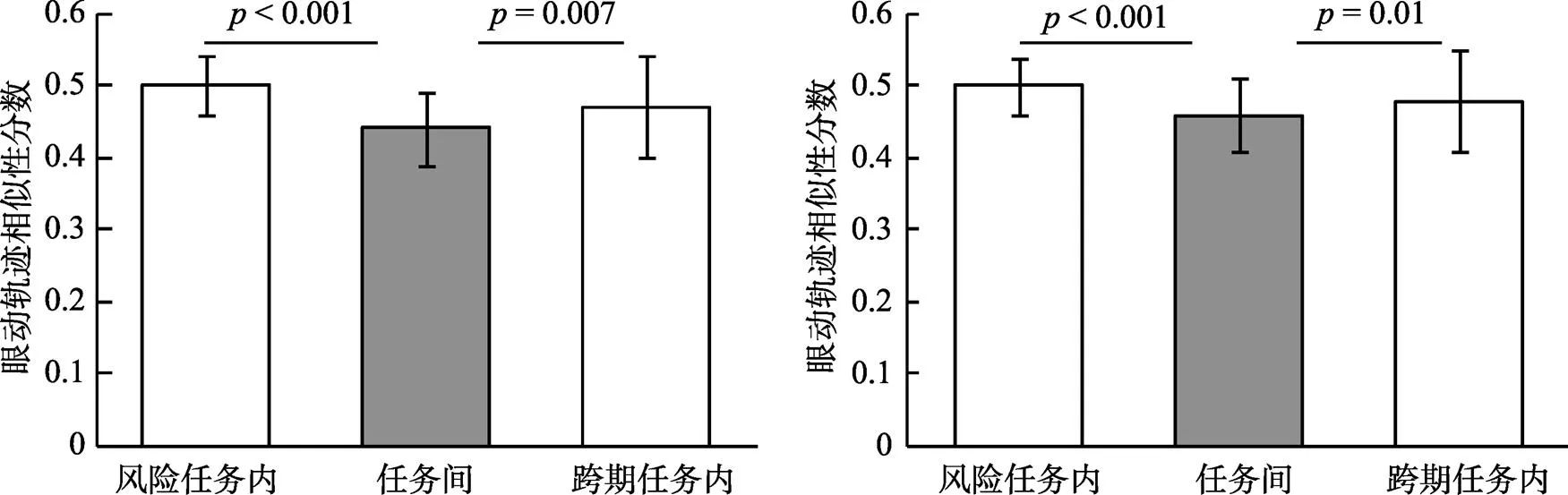
图7 眼动轨迹相似性分数比较结果(M ± SE)

(左：不含确定/即刻条件, 右：包含确定/即刻条件)

风险和跨期任务的典型试次如图8所示。K-S检验结果显示, 风险任务(不含确定:= 0.14,= 0.13; 包含确定:= 0.09,= 0.20)和跨期任务(不含即刻:= 0.06,= 0.20; 包含即刻:= 0.09,= 0.20)的任务内相似性分数均符合正态分布, 因此, 典型试次轨迹可代表任务条件内的平均眼动轨迹。通过观察典型试次, 我们可以发现, 相对而言, 风险任务中存在较多的基于维度眼跳, 然而跨期决策任务并未在整体眼动模式上体现出类似的眼动模式。此外, 与SM值的结果类似, 不含确定/即刻选项时, 存在更多基于维度眼跳, 包含确定/即刻选项时, 存在更多基于选项眼跳。

3.4 分层贝叶斯模型拟合

本研究分别对风险和跨期任务进行指数模型、双曲线模型和启发式模型的拟合。结果发现(表1), 无论是风险还是跨期任务, 相对于经典的基于选项加工的折扣模型(模型1、2), 基于维度加工的启发式模型(模型3)对风险和跨期任务的拟合度都更高, WAIC显著低于其他两个模型。且启发式模型对两个任务的结果预测率高达80%以上, 比折扣模型更能正确预测个体的选择, 以上结果支持H。根据ITCH模型的理论假设, 我们可以推测, 个体在风险和跨期决策中, 可能均采用了一系列简单启发式规则组合而成的策略, 例如, 先进行结果维度、概率/时间维度之间的比较, 然后做出决策。

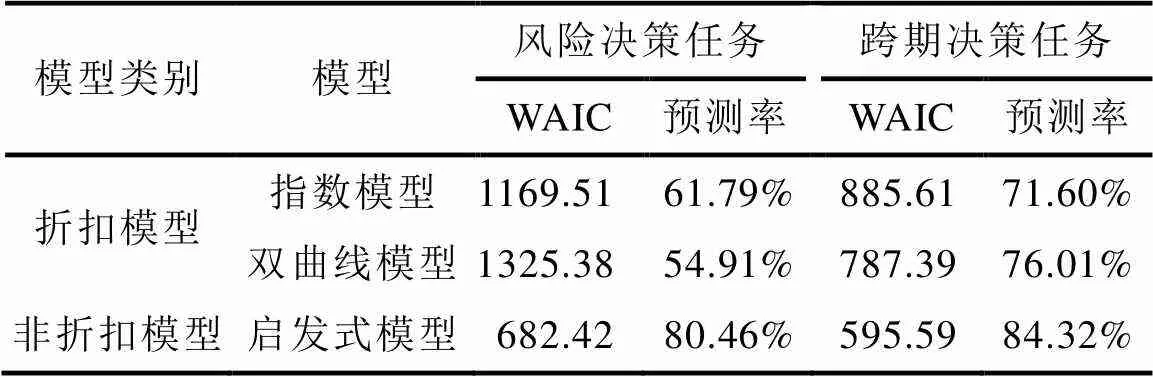
表1 分层贝叶斯模型拟合结果

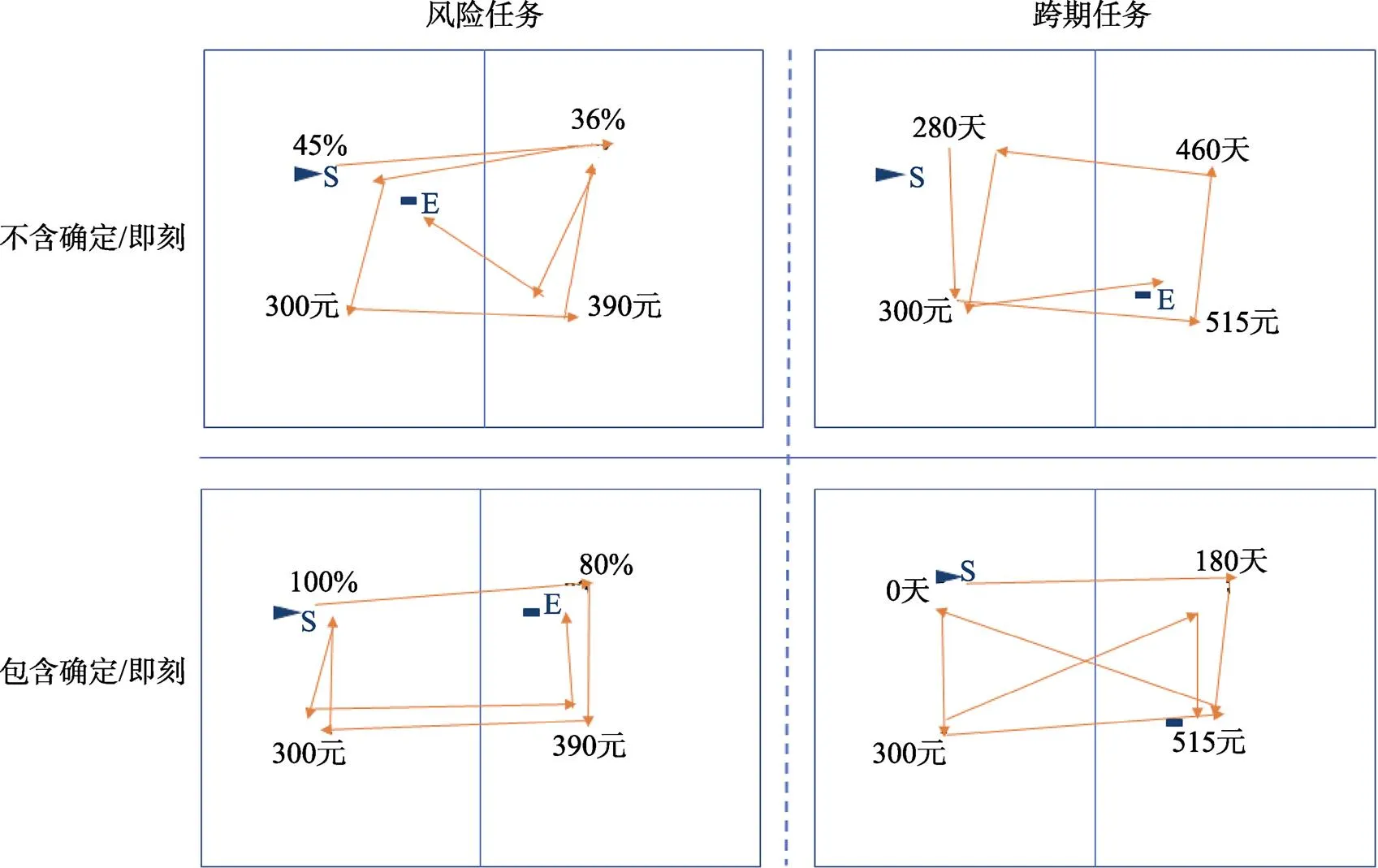
图8 各任务条件中典型试次的眼动轨迹

注：箭头代表眼动轨迹的方向, S代表起始位置, E代表终止位置。

表2 过程特征检验和模型拟合结果小结

4 讨论

本研究以确定效应和即刻效应为例, 从行为特征、局部和整体过程特征对风险和跨期决策进行了综合比较, 并通过分层贝叶斯模型拟合, 检验两类决策是否更符合非折扣模型的预测。结果表明, 对于行为特征, 个体过分偏好确定或即刻选项, 表现出了确定效应和即刻效应。对于局部过程特征, 二者的加工深度属性在所有参数条件下均相似; 但加工方向、加工复杂程度属性, 仅在包含确定/即刻选项的参数条件下相似。对于整体过程特征, 二者整体动态的眼动过程不同。对于模型拟合, 二者潜在认知过程相似, 均能更好地被非折扣模型拟合。以上结果表明, 风险和跨期决策在所检验的大多数属性上具有共同的过程机制, 且二者在加工过程上不符合补偿性模型折扣计算的假设, 更符合非补偿性的ITCH模型的假设, 可能采用了一系列启发式规则组合成的策略进行决策。

4.1 风险和跨期决策的共同过程机制

本研究基于“补偿/非补偿性”以及“基于维度/基于选项”规则的决策特征, 对两类决策的共同过程机制进行探索。发现二者核心的加工规则符合非补偿性的、基于维度的特征。

其中, 加工深度和复杂程度的结果说明, 二者均符合非补偿性加工规则：人们在做出决策前不会加工所有的选项特征, 而是依据部分信息进行决策; 且加工过程也可能不包含审慎的复杂计算过程。这一结果与前人, 如Stewart等人(2015)及Glöckner及同事(2011, 2012)的发现均一致。本研究发现两类决策过程中单个注视点平均时长较短(平均216 ms), 不符合补偿性规则的预期, 更支持启发式决策规则假设。此外, 本研究报告的决策前注视的选项特征数量为93.6%, 高于Su等人(2013)报告的平均注视量88.50%。这可能是由于本研究使用了单结果决策任务, 而Su等人(2013)使用的是双结果决策任务。由此可推测, 随着任务复杂程度增大, 人们在决策前所关注的信息量更小, 更不会进行补偿性加工。

加工方向和模型拟合的结果说明, 二者均符合基于维度的加工规则：人们在决策中更多地按照维度进行信息的搜索加工, 符合启发式模型的预测。这一结果和Su等人(2013)和Fisher等人(2013)的发现一致, 说明两类决策在信息比较过程中, 占优的搜索模式均为基于维度的比较。且这一基于维度比较的加工过程可以通过眼动过程真实地探测, 也可以通过模型拟合的方式被验证, 且二者结果一致, 更符合ITCH模型假设, 即决策者在风险和跨期决策中可能依据了一系列不同启发式规则的组合, 如对不同维度的绝对差异和相对差异等的比较, 且人们对不同的规则的使用赋予了不同的权重(Ericson et al., 2015)。尽管本文仅选用了ITCH作为基于维度加工模型代表, 但考虑到不同加工模型的研究中, 基于维度加工模型家族的解释力差异不大(Ericson et al., 2015), 但相对基于选项加工模型均表现更好(Dai & Busemeyer, 2014; Scholten & Read, 2010)。因此我们推测, 未来研究如选用其他启发式模型, 有可能得到相似的结果：相对于基于选项加工的折扣模型, 基于维度加工的启发式模型对风险和跨期任务的拟合度更高。

需要注意的是, 贝叶斯因子分析的结果显示, 在不含确定/即刻选项条件下, 只有较弱的证据支持两类决策的加工方向一致, 但考虑到二者的SM值与0差异均显著, 即表现出基于维度加工。因此, 定性而言, 两类决策在加工方向上具有相似性。

综上, 本研究证实了决策主流理论中所一致接受的折扣计算(或加权求和)过程未必适用于风险和跨期决策, 未来的研究在尝试建立二者共同理论框架时, 或应考虑非折扣模型。

4.2 风险和跨期决策过程的特异性

本研究亦发现两类决策在少数行为和过程特征上存在特异性：相对于风险决策, 人们进行跨期决策的时间更长, 加工复杂度和加工深度更高(不含确定/即刻选项时), 且在整体过程特征上, 风险任务中基于维度比较特征更显著。尤其在观察典型试次的结果可见, 二者在整体动态眼动过程上的差异可能体现在信息比较的模式上：在不含确定选项的风险任务中, 个体相继进行基于概率和结果维度的信息比较然后做出决策, 然而在跨期决策中并未体现出类似的眼动模式。

这些特异性的存在可能有两个原因：其一, 与跨期决策相比, 风险决策可能更接近自动化、平行的加工方式, 而人们进行跨期决策时, 尤其在不含即刻选项时, 审慎程度或加工难度可能相对更高。其二, 研究中两个任务的部分材料(不含确定/即刻选项条件)仅匹配了结果的大小, 但并未对概率和时间的大小按照其心理感受进行等量匹配, 如45%的概率获得300元, 其心理感受可能并不等价于280天后获得300元。未来研究可针对两种决策任务设置匹配的实验参数, 以避免参数差异对结果带来的混淆。

4.3 确定和即刻信息在风险和跨期决策过程中的特异性

本研究发现两类决策中是否包含确定/即刻选项在各局部过程特征上均存在差异, 这说明个体对确定和即刻信息的加工具有特异性：当不含确定/即刻选项时, 人们更倾向于按照偏向补偿性规则及基于维度的规则决策：当不含确定/即刻选项时, 决策的加工复杂程度更高, 加工深度更深, 加工方向更基于维度; 但当包含确定/即刻选项时, 人们在加工方向上并无占优的模式。

本研究发现的确定/即刻选项的特异性, 与前人对确定和即刻效应的解释一致, 即个体对确定选项和即刻选项赋予过高权重(Kahneman & Tversky, 1979; Kirby & Herrnstein, 1995)。由于高权重, 个体对这些信息的注意时间更短, 可能更不需要进行深度加工, 或依赖其与风险/将来选项的相对评估和比较, 即可对确定/即刻选项进行效用评估。此外, 确定/即刻的参数信息在本研究实验中固定不变, 相对非确定/即刻的参数来说认知难度更小, 随着实验进行, 更容易被忽略。

值得注意的是, 确定和即刻信息的这一特异性说明, 特异的参数或情境对风险和跨期决策的加工存在较大影响, 因此, 未来研究中应关注非特异参数情境中两类决策的比较。

4.4 研究意义

本文在理论和方法上进行了几方面的积极探索。在理论层面, 我们发现风险和跨期决策具有共同的过程机制, 为建立两类决策的共同解释框架做出了有益的尝试, 将有助于未来研究从本质上认识人类决策的内在机制, 发展出同时适用于风险决策与跨期决策的普遍性决策理论。未来研究或可基于两类决策其他对应的行为效应进行比较, 如量级效应(magnitude effect), 进一步考察二者的相似性和特异性。

在方法层面, 本研究综合了眼动过程和结果的多维度数据, 并使用新近的眼动轨迹分析法, 有利于多层次地认识风险和跨期决策的差异以及共同机制, 尝试克服以往研究忽视决策模型中信息搜索与评价的动态序列过程假设的不足。未来研究应基于整体动态视角, 考察决策过程的时间序列等整体的过程属性, 并考虑多种决策过程或策略共存的情况, 即基于不同实验参数条件, 如是否在无差别点(indifference point)附近, 决策者可能采用不同的决策策略。这种策略的区分或可依据分析不同参数条件的眼动轨迹等指标来实现。

特别地, 在计算建模层面, 本研究采用分层贝叶斯模型拟合法, 同时估计个体层面和群体层面的参数, 对结果进行更精确的估计(Vincent, 2016), 有效克服本领域以往模型拟合研究(Green et al., 1999; Myerson, Green, Hanson, Holt, & Estle, 2003)受限于数据样本大小、被试个体差异的弱点, 为“相对于经典的折扣计算模型, 风险和跨期决策是否可以被启发式模型更好地预测”这一问题提供了更为精确的解答。

4.5 研究的不足

本研究存在以下不足。首先, 本研究只涉及了获益框架, 没有进一步讨论风险和跨期决策在损失框架、损益混合框架的异同。在生活中, 非获得框架的风险和跨期决策普遍存在, 且获得与损失具有不对称性：获得领域的折扣程度比损失领域更大, 人们在面临获得和损失时可能采用不同的决策策略(Kahneman & Tversky, 1979; Zhang et al., 2016)。因此, 基于获得框架的研究结果难以直接推广到其他框架, 未来的研究应针对损失或损益混合框架, 对风险和跨期决策进行进一步地比较。

其次, 本研究对所有被试采用统一的、自行设定的概率或时间参数, 忽略了概率和时间参数的等量转换关系, 以及参数设置的个体差异。概率和时间参数取值分别对两类决策的属性有很大影响, 不同的参数取值可导致行为和过程差异, 无法排除由参数效应给实验结果带来的可能偏差。此外, 对不同个体采用同一套风险和跨期决策的题目也可能难以排除个体差异对结果带来的混淆。未来的研究可充分考虑概率和时间的等量对应关系, 以及决策中个体偏好的差异, 以更好地控制参数差异对结果可能造成的影响。

最后, 未来研究或可基于神经基础层面, 借助基于模型的脑认知神经方法(model-based neuroimaging)对两类决策进行神经影像学的比较, 探索二者共同的神经机制。

5 结论

本研究以确定效应和即刻效应为例, 对风险和跨期决策进行了决策过程的比较, 结合行为、局部及整体过程特征和模型拟合的证据, 发现：1)在决策基本规则上, 风险和跨期决策具有共同机制, 都不遵循折扣模型所假设的补偿性的、基于选项的加工规则, 更可能依据简捷的、非补偿性模型所预期的启发式规则决策; 2)风险和跨期决策的过程存在部分特异性：跨期决策的加工复杂程度、加工深度均高于风险决策, 且二者整体动态的眼动过程存在差异; 3)风险决策的确定信息和跨期决策的即刻信息在过程机制上存在特异性：当不包含确定/即刻选项时, 个体加工的补偿性程度更高, 更倾向于采用基于维度的加工方式, 但包含确定/即刻选项时, 个体加工的补偿性程度更低, 不具有占优的加工方式。

Ahn, W.-Y., Haines, N., & Zhang, L. (2017). Revealing neuro- computational mechanisms of reinforcement learning and decision-making with the hBayesDM package.,, 24–57. doi: 10.1162/cpsy_a_00002

Allais, M. (1953). Le comportement de l'homme rationnel devant le risque: Critique des postulats et axioms de l'ecole americaine [Rational man's behavior in face of risk: Critique of the American School's postulates and axioms].503–546.

Böckenholt, U., & Hynan, L. S. (1994). Caveats on a process- tracing measure and a remedy.(2)103–117. doi: 10.1002/bdm.3960070203

Brandstätter, E., Gigerenzer, G., & Hertwig, R. (2006). The priority heuristic: Making choices without trade-offs.(2)409–432. doi: 10.1037/0033-295X.113.2.409

Brandstätter, E., & Körner, C. (2014). Attention in risky choice.,, 166–176. doi: 10.1016/j.actpsy.2014. 08.008

Burnham, K. P., & Anderson, D. R. (2004). Multimodel inference: Understanding AIC and BIC in model selection.,(2), 261–304. doi: 10.1177/0049124104268644

Dai, J., & Busemeyer, J. R. (2014). A probabilistic, dynamic, and attribute-wise model of intertemporal choice.(4)1489–1514. doi: 10.1037/a0035976

Ericson, K. M. M., White, J. M., Laibson, D. I., & Cohen, J. D. (2015). Money earlier or later? Simple heuristics explain intertemporal choices better than delay discounting does.,(6), 826–833. doi: 10.1177/ 0956797615572232

Fiedler, S., & Glöckner, A. (2012). The dynamics of decision making in risky choice: An eye-tracking analysis.,335. doi: 10.3389/fpsyg.2012.00335

Figner, B., Knoch, D., Johnson, E. J., Krosch, A. R., Lisanby, S. H., Fehr, E., & Weber, E. U. (2010). Lateral prefrontal cortex and self-control in intertemporal choice.,(5), 538–539. doi: 10.1038/nn.2516

Fisher, G., & Rangel, A. (2013).. Paper presented atSociety for Judgment and Decision Making Annual Conference, Toronto, Canada.

Franco-Watkins, A. M., Mattson, R. E., & Jackson, M. D. (2016). Now or later? Attentional processing and intertemporal choice.(2-3)206–217. doi: 10.1002/bdm.1895

Frederick, S., Loewenstein, G., & O'donoghue, T. (2002). Time discounting and time preference: A critical review.(2), 351–401. doi: 10.1257/ 002205102320161311

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2014).(3rd ed.). New York, NY: CRC Press.

Gelman, A., & Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences.,(4), 457–472. doi: 10.1214/ss/1177011136

Glöckner, A., & Herbold, A- K. (2011). An eye-tracking study on information processing in risky decisions: Evidence for compensatory strategies based on automatic processes.(1)71–98. doi: 10.1002/bdm.684

Green, L., Myerson, J., & Ostaszewski, P. (1999). Amount of reward has opposite effects on the discounting of delayed and probabilistic outcomes.(2), 418–427. doi: 10.1037/0278-7393.25.2.418

Green, L., Myerson, J., & Vanderveldt, A. (2014) Delay and probability discounting. In: F. K. McSweeney & E. Murphy (ds.),(pp. 307–337). Chichester, England: Wiley.

Hardisty, D. J., & Pfeffer, J. (2016). Intertemporal uncertainty avoidance: When the future is uncertain, people prefer the present, and when the present is uncertain, people prefer the future.,(2), 519–527. doi: 10.1287/mnsc.2015.2349

Horstmann, N. (2009). How distinct are intuition and deliberation? An eye-tracking analysis of instruction-induced decision modes.,(5), 335–354. doi: 10.2139/ssrn.1393729

Hu, C-P., Kong, X-Z., Wagenmakers, E-J., Ly, A., & Peng K-P. (2018). The bayes factor and its implementation in JASP: A pratical primer.(6)951–965. doi: 10.3724/SP. J.1042.2018.00951

[胡传鹏, 孔祥祯, Wagenmakers, E-J., Ly, A., 彭凯平. (2018). 贝叶斯因子及其在JASP中的实现.,(6)951–965.]

JASP Team. (2017). JASP (Version 0.8.2) [Computer software]

Jeffreys, H. (1961).(3rd ed.). Oxford, UK: Oxford University Press.

Kable, J. W., & Glimcher, P. W. (2007). The neural correlates of subjective value during intertemporal choice.,(12), 1625–1633. doi: 10.1038/nn2007

Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk.(2)263–291. doi: 10.2307/1914185

Kahneman, D., & Tversky, A. (1984). Choices, values, and frames.(4), 341–350.

Kirby, K. N., & Herrnstein, R. J. (1995). Preference reversals due to myopic discounting of delayed reward.,(2), 83–89. doi: 10.1111/j.1467-9280.1995.tb00311.x

Konstantinidis, E., van Ravenzwaaij, D., & Newell, B. R. (2017). Exploring the decision dynamics of risky intertemporal choice., 694-699. Retrieved from https://pdfs.semanticscholar.org/68cb/ebe19485a7c8ed97948ecec6b0aa6fd49e92.pdf

Kuhnen, C. M., & Knutson, B. (2005). The neural basis of financial risk taking.,(5), 763–770. doi: 10.1016/j.neuron.2005.08.008

Li, S. (2004). A behavioral choice model when computational ability matters.(2)147–163. doi: 10.1023/B:APIN.0000013337.01711.c7

Li, S., Su, Y., & Sun, Y. (2010). The effect of pseudo-immediacy on intertemporal choices.(6), 781–787. doi: 10.1080/13669870903551704

Liang., Z-Y., Zhou, L., & Su, Y. (2016, Aug.). The hidden-zero effect in risky choice: An eye-tracking study. Paper presented at the, Yokohama, JAPAN.

Luckman, A., Donkin, C., & Newell, B. R. (2017). Can a single model account for both risky choices and inter-temporal choices? Testing the assumptions underlying models of risky inter-temporal choice.,785–792. doi: 10.3758/s13423-017-1330-8

Loewenstein, G., & Prelec, D. (1992). Anomalies in intertemporal choice: Evidence and an interpretation.(2), 573–597. doi: 10.1006/obhd.1996.0028

Ly, A., Verhagen, J., & Wagenmakers, E.-J. (2016a). An evaluation of alternative methods for testing hypotheses, from the perspective of Harold Jeffreys.,, 43–55. doi: 10.1016/j.jmp.2016.01.003

Ly, A., Verhagen, J., & Wagenmakers, E-J. (2016b). Harold Jeffreys’s default Bayes factor hypothesis tests: Explanation, extension, and application in psychology.,, 19–32. doi: 10.1016/j.jmp. 2015.06.004

Magen, E., Dweck, C., & Gross, J. J. (2008). The hidden-zero effect: Representing a single choice as an extended sequence reduces impulsive choice.(7)648–649. doi: 10.1111/j.1467-9280.2008.02137.x

Marsman, M., & Wagenmakers, E-J. (2017). Bayesian benefits with JASP.(5), 545–555. doi: 10.1080/17405629.2016.1259614

Mazur, J. E. (1987). An adjusting procedure for studying delayed reinforcement. In M. L. Commons, J. E. Mazur, J. A. Nevin, & H. Rachlin (s.),(pp. 55–73). Hillsdale, NJ: Erlbaum.

McClure, S. M., Laibson, D. I., Loewenstein, G., & Cohen, J. D. (2004). Separate neural systems value immediate and delayed monetary rewards.,(5695), 503–507. doi: 10.1126/science.1100907

Myerson, J., Green, L., Hanson, S. J., Holt, D. D., & Estle, S. J. (2003). Discounting delayed and probabilistic rewards: Processes and traits.(5), 619–635. doi: 10.1016/S0167-4870(03)00005-9

Noton, D., & Stark, L. (1971). Scanpaths in eye movements during pattern perception.(3968)308–311. doi: 10.1126/science.171.3968.308

Pascal, B. (1670).(W. F. Trotter, Trans.). Retrieved Nov. 22, 2018, from https://sourcebooks.fordham.edu/mod/ 1660pascal-pensees.asp

Rao, L-L., & Li, S. (2011). New paradoxes in intertemporal choice.(2), 122–129.

Rayner, K. (.) (2013).. New York: Springer-Verlag. doi: 10.1007/978-1-4612-2852-3

Read, D., Frederick, S., & Scholten, M. (2013). DRIFT: An analysis of outcome framing in intertemporal choice.,(2), 573–588. doi: 10.1037/a0029177

Read, D., Loewenstein G., & Kalyanaraman, S. (1999). Mixing virtue and vice: Combining the immediacy effect and the diversification heuristic.,(4), 257–273. doi: 10.1002/(SICI)1099-0771 (199912)12:4%3C257::AID-BDM327%3E3.0.CO;2-6

Reeck, C., Wall, D., & Johnson, E. J. (2017). Search predicts and changes patience in intertemporal choice.,(45), 11890– 11895. doi: 10.1073/pnas.1707040114

Rouder, J. N., Speckman, P. L., Sun, D. C., Morey, R. D., & Iverson, G. (2009). Bayesian t-tests for accepting and rejecting the null hypothesis., 225–237. doi: 10.3758/PBR.16.2.225

Samuelson, P. A. (1937). A note on measurement of utility.(2), 155–161.

Scheibehenne, B., & Pachur, T. (2015). Using Bayesian hierarchical parameter estimation to assess the generalizability of cognitive models of choice.,(2), 391–407. doi: 10.3758/s13423-014-0684-4

Schneider, E., Streicher, B., Lermer, E., Sachs, R., & Frey, D. (2017). Measuring the zero-risk bias: Methodological artefact or decision-making strategy?,, 31–44. doi:10.1027/2151-2604/a000284

Schulte-Mecklenbeck, M., Johnson, J. G., Böckenholt, U., Goldstein, D. G., Russo, J. E., Sullivan, N. J., & Willemsen, M. C. (2017). Process-tracing methods in decision making: On growing up in the 70s.,(5), 442–450. doi: 10.1177/0963721417708229

Schulte-Mecklenbeck, M., Kühberger, A., Gagl, B., & Hutzler, F. (2017). Inducing thought processes: Bringing process measures and cognitive processes closer together.,(5), 1001–1013. doi: 10.1002/bdm.2007

Scholten, M., & Read, D. (2010). The psychology of intertemporal tradeoffs.(3), 925–944. doi: 10.1037/a001

Simon, H. A. (1982).. Cambridge, US: MIT Press.

Stewart, N., Hermens, F., & Matthews, W. J. (2015). Eye movements in risky choice.,(2-3), 116–136. doi: 10.1002/bdm.1854

Stevens, J. R. (2011). Mechanisms for decisions about the future. In R. Menzel, & J. Fischer (s.)(pp. 93– 104). Cambridge, MA: MIT Press.

Stevenson, M. K., Busemeyer, J. R., & Naylor, J. C. (1990). Judgment and decision-making theory. In D. M. Dunnette, & L. M. Hough (Eds.)(pp. 283–374). CA, US: Consulting Psychologists Press.

Su, Y., Rao, L. L., Sun, H. Y., Du, X. L., Li, X., & Li, S. (2013). Is making a risky choice based on a weighting and adding process? An eye-tracking investigation.(6)1765–1780. doi: 10.1037/a0032861

Vehtari, A., Gelman, A., & Gabry, J. (2015). Efficient implementation of leave-one-out cross-validation and WAIC for evaluating fitted Bayesian models.. doi: 1007/s11222-016-9696-4

Vincent, B. T. (2016). Hierarchical Bayesian estimation and hypothesis testing for delay discounting tasks.,, 1608–1620. doi: 10.3758/s13428-015- 0672-2

Wagenmakers, E-J., Love, J., Marsman, M., Jamil, T., Ly, A., Verhagen, J., … van Doorn, J. (2018a). Bayesian inference for psychology. Part II : Example applications with JASP.,(1), 58–76. doi: 10.3758/s13423-017-1323-7

Wagenmakers, E.- J., Marsman, M., Jamil, T., Ly, A., Verhagen, J., Love, J., … Morey, R. D. (2018b). Bayesian inference for psychology. Part I: Theoretical advantages and practical ramifications.,(1), 35–57. doi: 10.3758/s13423-017-1343-3

Wang Z-J., & Li S. (2012). Tests of the integrative model and priority heuristic model from the point of view of choice process: Evidence from an eye-tracking study.,(2)179–198. doi: 10.3724/SP.J.1041.2012.00179

[汪祚军, 李纾. (2012). 对整合模型和占优启发式模型的检验：基于信息加工过程的眼动研究证据.(2)179–198.]

Weber, B. J., & Chapman, G. B. (2005). The combined effects of risk and time on choice: Does uncertainty eliminate the immediacy effect? Does delay eliminate the certainty effect?(2), 104–118. doi: 10.1016/j.obhdp.2005.01.001

Weber, B. J., & Huettel, S. A. (2008). The neural substrates of probabilistic and intertemporal decision making., 104-115. doi: 10.1016/j.brainres.2008.07.105

Wei, Z-H., & Li, X. S. (2015). Decision process tracing: Evidence from eye-movement data.(12)2029–2041. doi: 10.3724/SP.J.1042.2015.02029

[魏子晗, 李兴珊. (2015). 决策过程的追踪: 基于眼动的证据.(12), 2029–2041.]

Wu F., Gu Q., Shi Z-H., Gao Z-F., & Shen M-W. (2018). Striding over the “classical statistical inference trap” —Application of Bayes factors in psychological studies. Chinese Journal of Applied Psychology, 24(3), 195–202.

[吴凡, 顾全, 施壮华, 高在峰, 沈模卫. (2018). 跳出传统假设检验方法的陷阱——贝叶斯因子在心理学研究领域的应用. 应用心理学, 24(3), 195–202.]

Wu Y., Zhou X-L., & Luo Y-J. (2010). The neuroscience of intertemporal choices and decision-making under risk and uncertainty.,(1), 76-80.

[吴燕, 周晓林, 罗跃嘉. (2010). 跨期选择和风险决策的认知神经机制.,(1), 76–80.]

Zhang, Y-Y., Xu, L-J., Rao, L-L., Zhou, L., Zhou, Y, Jiang, T-Z, Li, S., & Liang, Z-Y. (2016). Gain-loss asymmetry in neural correlates of temporal discounting: An approach-avoidance motivation perspective., 31902. doi: 10.1038/srep31902

Zhou, L. (2017).(Unpublished Doctoral dissertation). University of Chinese Academy of Sciences, Beijing, China.

[周蕾(2017).(博士学位论文). 中国科学院大学.]

Zhou, L., Zhang Y-Y., Li S.& Liang, Z-Y. (2018). New paradigms for the old question: Challenge the expectation rule held by risky decision-making theories.,, e17. doi:10.1017/prp.2018.4

Zhou, L., Zhang, Y-Y., Wang, Z-J., Rao, L-L., Wang, W., Li, S., Li, X. S., & Liang, Z-Y. (2016). A scanpath analysis of the risky decision-making process.(2-3), 169–182. doi: 10.1002/bdm.1943

① 在0附近相对概率密度更小的柯西分布允许更多的大效应, 因此被认为更适合于备择假设的先验分布(Jeffreys, 1961; Ly, Verhagen, & Wagenmakers, 2016a, 2016b; Rouder et al., 2009)。

Similarity in processes of risky choice and intertemporal choice: The case of certainty effect and immediacy effect

ZHOU Lei; LI Ai-Mei; ZHANG Lei; LI Shu; LIANG Zhu-Yuan

(Management School, Jinan University, Guangzhou 510632, China)(CAS Key Laboratory of Behavioral Science, Institute of Psychology, Beijing 100101, China)(Department of Psychology, University of Chinese Academy of Sciences, Beijing 100049, China)(Institute for Systems Neuroscience, University Medical Center Hamburg-Eppendorf, Hamburg 20246, Germany)

Risky choice (RC) and intertemporal choice (IC) are two types of common decisions that are vital to human’s everyday life. RC and IC share similarities regarding theoretical development, behavioral effects, and neural basis. One critical challenge is that, although previous studies have revealed that RC and IC involve similar cognitive processes, results are mixed regarding what the exact mechanism might be. The mainstream discounting model hypothesizes that both RC and IC follow aandrule. However, other models suggest that RC and IC commonly involve-andprocessing. Moreover, prior studies primarily based their findings on outcome data and few have attempted to determine whether RC and IC shared a common decision process at the cognitive computational level.

To fill this gap, the present study adopts a systematic approach to disentangle the exact mechanism of RC and IC. We considered two well-studied behavioral effects, namely,of RC andof IC, respectively, and compared their underlying local and holistic process characteristics by using eye-tracking technique. Besides, we employed hierarchical Bayesian modeling to assess whether alternative- or attribute-based models better fit both RC and IC. We designed a 2×2 within-subject paradigm, with the choice task (RC vs. IC) and the construct of decision options (with vs. without certain/immediate option) as factors. Thirty-three postgraduate students participated in our study. As we were particularly interested in two pairs of decision rules, i.e.,rules andrules, we included a series of decision attributes that reflected them, based on the local and holistic process characteristics derived from eye-movement data to test our hypotheses.

Our entire set of analyses aimed to (1) determine whether the decision processes of RC and IC are similar and (2) identify the best computational model that is more suitable for both decisions. For the first aim, results show that RC and IC indeed share comparable decision processes, albeit having a few differences in other aspects. Specifically, RC and IC differ in process characteristics, such as complexity and holistic eye-movement dynamics, and IC is processed in a relatively more deliberate, deeper fashion than RC. However, they are similar in other characteristics, such as search direction, which is more relevant to making decisions. For the second aim, computational modeling of process characteristics suggests that both types of decisions are consistent with non-discounting models. In particular, results of search direction, in light of Bayesian model comparison, reveals that participants are more likely to follow therule rather than therule when deciding for both RC and IC. Furthermore, different task constructs of decision options,, show distinct process characteristics, such as direction, complexity, and depth in both RC and IC.

To conclude, the present study shows that although differences exist between RC and IC, they indeed have shared cognitive mechanisms at the core of the decision processes. In both types of decisions, contrary to classic discounting models, individuals seem not to followrules, which undergoes a “weighting and summing” or “delay discounting” process. Instead, they are more likely to use simple heuristic rules hypothesized by non-discounting models. Moreover, when including certain or immediate options, individuals tend to follow lessand non-dominant (neithernor) rules. In sum, our findings not only provide a theoretical and empirical basis for the establishment of a common framework for RC and IC, but also provide a novel direction for thorough theoretical and methodological comparisons between variant decision tasks.

risky choice; intertemporal choice; eye-tracking; hierarchical Bayesian modeling; certainty effect; immediacy effect

B849: C91

10.3724/SP.J.1041.2019.00337

2018-05-11

* 国家自然科学基金青年项目(71801110), 国家自然科学基金面上项目(71471171, 31471005, 71571087), 教育部人文社会科学研究青年基金项目(18YJC630268), 中国博士后科学基金资助项目(2018M633270), 中国科学院行为科学重点实验室自主研究课题项目(Y5CX052003), 广东省自科重大培育项目(2017A030308013)资助。

梁竹苑, Email: liangzy@psych.ac.cn; 李纾, Email: lishu@psych.ac.cn