波动率期限结构分析及在期权定价交易中的应用

李雪飞 赵冰 严高剑

(中信证券股份有限公司，北京 100026)

引言

Black-Scholes模型是期权定价、交易中应用最广泛的模型。在标的收益率正态分布、波动率为常数等模型前提假设下，将得出同一标的的期权隐含波动率相同且等于常数波动率的结论。然而现实中标的特性并不完全满足模型假设，导致B-S算法下不同到期日、不同行权价的期权合约隐含波动率不一致即期权隐含波动率是一个曲面。对隐含波动率曲面的估计是期权定价的核心之一。

期权隐含波动率曲面包含不同到期日合约隐含波动率的期限结构，以及相同到期日、不同行权价合约的隐含波动率微笑形态两个方面。一种对其进行估计的方法是将满足一定流动性要求、实虚度要求的合约汇总在一起统一进行处理。然而在先前的建模中发现，由于50ETF期权仅有4个月份、时间项的自由度较低，把期限结构和微笑曲面一并建模时会影响估计效果。因此本文中仅考虑隐含波动率期限结构、不考虑波动率微笑方面的影响。

具体的做法上，本文首先考察了50ETF的波动数据，分析不同的50ETF历史波动率环境下、未来不同期限的实际波动率的分布情况，并将其期望值作为未来给定期限的平值期权合约隐含波动率的一个理论估计；其次，使用50ETF期权数据，计算出不同市场环境下、不同期限的平值合约隐含波动率的实际值，并与理论估计值进行对比；最终，文中构建了一个交易模型，使用各期限的平值跨式组合捕捉前面二者的差异带来的收益，并进行了实证检验。

从2015年2月9日上交所50ETF期权正式上线至今已接近4年，市场中新的股票、商品期权标的逐渐增加，未来新的期权标的品种也将逐步问世。在此背景下，本文通过对期权波动率曲面的分析，对探索期权的定价和价格发现机制、指导实际的期权交易均具备一定的价值。

50ETF期权隐含波动率期限结构的理论解

常数波动率框架下，给定期限的期权合约隐含波动率合理值应该等于该期限中的标的实际波动率。一方面，这是B-S公式可以直接推出的结果；另一方面，不考虑交易及摩擦成本的情况下，隐含波动率不等于实际波动率便可通过期权复制的交易获得正期望的套利收益。

下图为一个标的实际波动率30%，一个月到期的平值认沽期权合约隐含波动率恒定为20%的例子。在该假设下，投资者买入认沽期权合约并使用现货逐日对冲Delta风险，在生成的100000条随机路径上的组合最终累计盈亏分布如图1所示，其中方案一、二为选用了不同的对冲波动率时的结果。从图中可以看到，不同的对冲方案下累计盈亏的分布会有所差别，但期望收益均为0.0117，均等于所选期权合约的Vega值(0.117)与波动率差值(10%)的乘积。此时，在正期望收益的影响下，统计套利投资者将大量进入市场进入上述交易，买入提升认沽期权的隐含波动率、直至隐含波动率与实际波动率差值降低、套利收益小于成本时达到平衡。

反之，在隐含波动率大幅高于实际波动率时，统计套利交易者同样会进入市场进入卖出期权和Delta对冲的操作，使实际波动率和隐含波动率的差值收窄。

由上，在恒定波动率的框架下，期权合约隐含波动率合理值应该等于未来该段时间中标的实际波动率。因此，探寻期权隐含波动率期限结构的理论解实际上是要对未来不同区间段的实际波动率进行估计。本文以50ETF过去一段时间的历史波动率作为条件变量，对“已知过去20日标的实际波动率，未来不同期限实际波动率分布如何？”这一问题加以探讨。

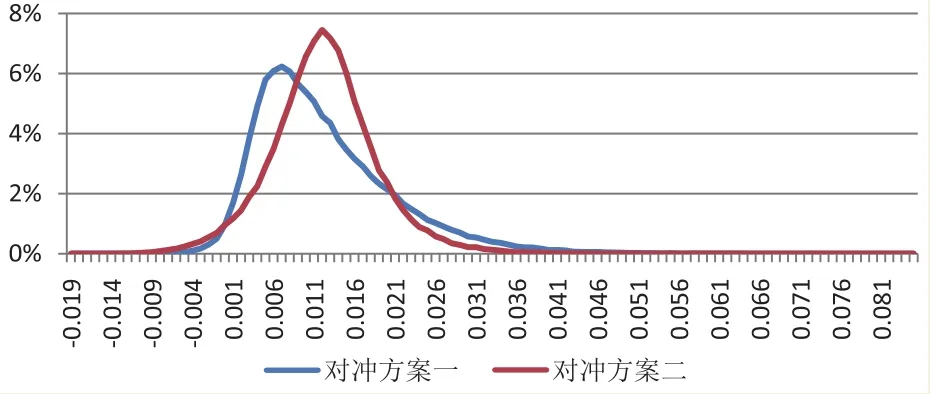
图1 100000条随机路径上的组合累计盈亏分布

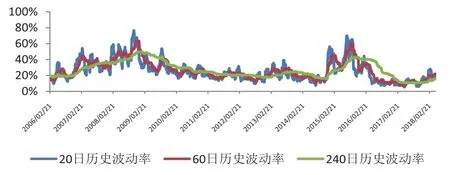
图2 2006年2月21日～2018年5月8日，50ETF20日、60日、240日历史波动率变化图

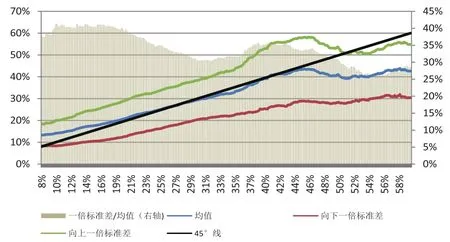
图3 20日历史波动率对应的20日未来波动率分布

图2为2006年2月21日～2018年5月8日的50ETF20日、60日、240日历史波动率变化图。可以看到，短周期的历史波动率变化频率相对较高，长周期的历史波动率变化频率相对较低；各期限的历史波动率均是在一定范围内上下波动；高波动及低波动的市场环境具有一定的延续性。

本文首先考虑过去20日波动率与未来20日波动率的关系，如图3，将20日历史波动率差距在5%以内的样本点聚在一起，计算其均值及上下浮动一倍标准差的范围。从中可以看出均值回复的特征：历史波动率在25～45%的范围中时，未来波动率均值与历史波动率高度一致；历史波动率较低时，未来波动率均值高于历史波动率；历史波动率较高时，未来波动率均值低于历史波动率。

将图3中的数据按每5%的历史波动率区间做一个分组，计算转移概率如表1，其中上升是指波动率增加10%以上(例如，历史波动率20%，未来波动率超过22%)；下降是指波动率降低10%以上；不变指波动率变化不足10%。从中也可以得到类似前文的均值回复结论。

进一步分析，针对“给定过去20日历史波动率，不同期限的未来波动率分布如何？”的问题来分析数据。表2中是20日历史波动率取不同值时，对应的未来20、41、61、122个交易日的波动率的分布情况。从中可以看到，以20日历史波动率作为条件变量，各周期的未来波动率变化具备均值回复的共性特征，但是边界位置略有差别。

从前文中可以得到几个结论：

首先，波动率存在聚集效应：较高的历史波动率对应的未来波动率平均意义上看也较高，有正相关性。

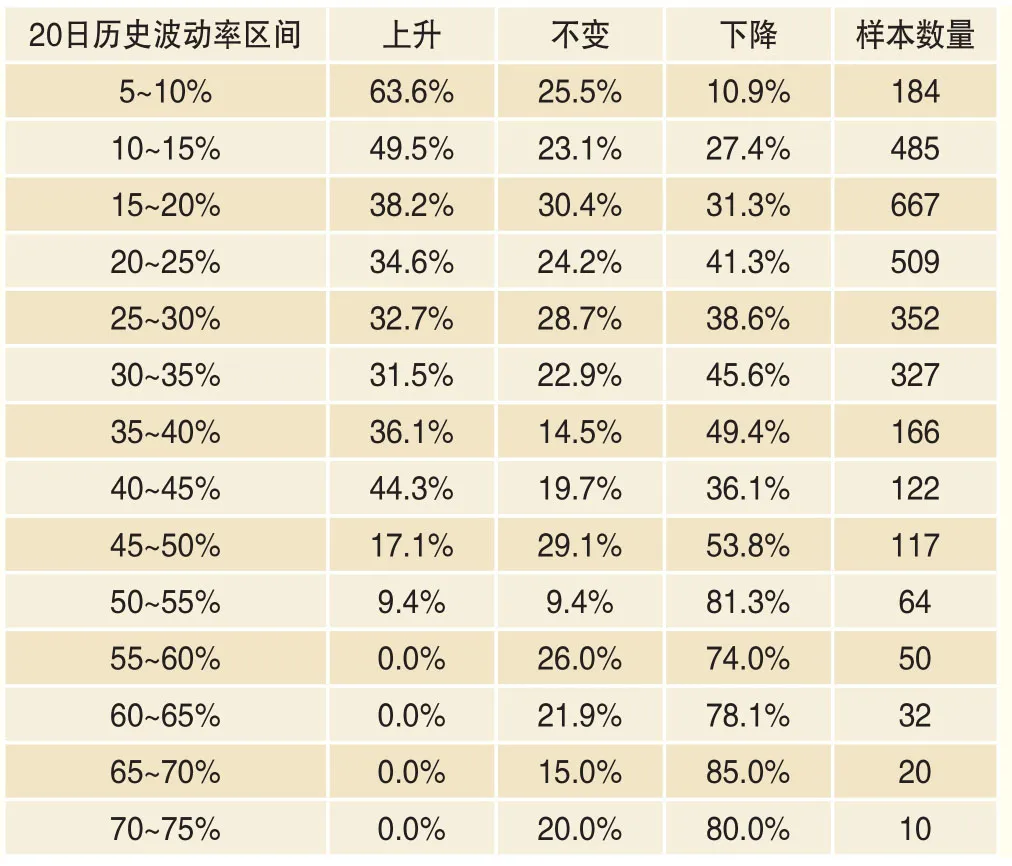
表1 20日历史波动率与未来波动率的转移概率矩阵

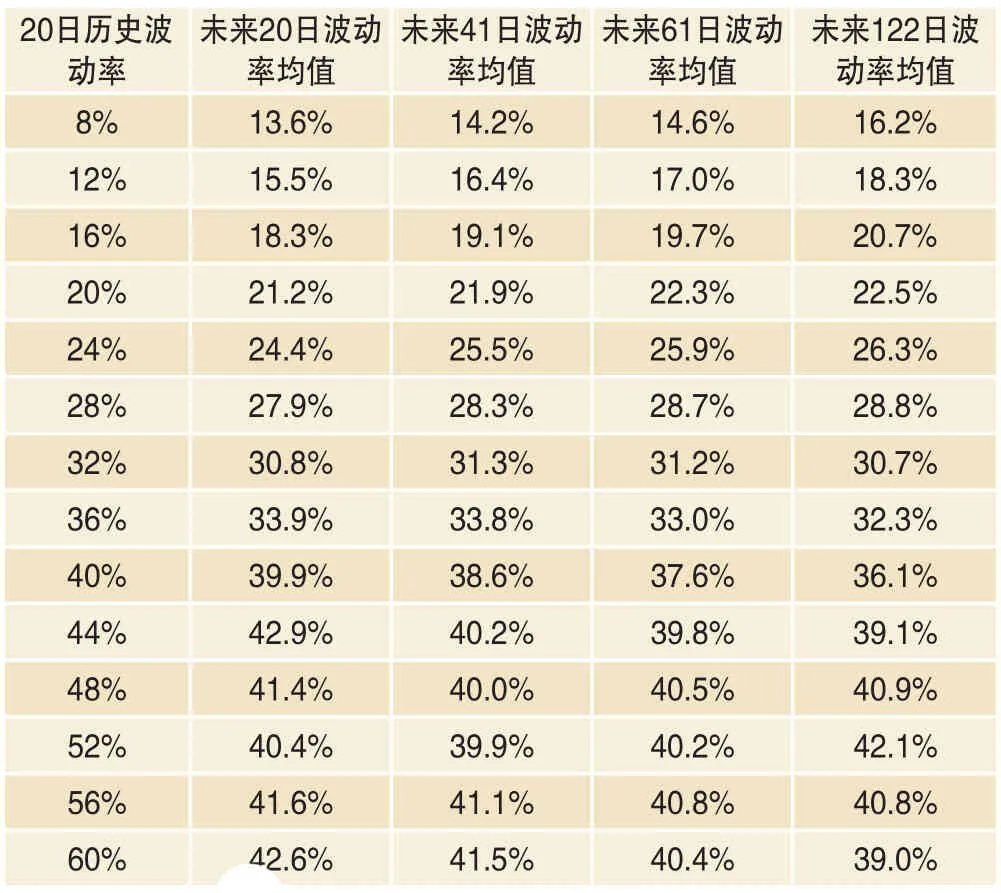
表2 20日历史波动率对应的不同周期未来波动率均值

其次，波动率存在均值回复特性：整体上看，相同时间长度的历史波动率很低时，未来波动率均值高于历史波动率；历史波动率很高时，未来波动率均值低于历史波动率；历史波动率大致在20～40%范围的，未来波动率均值与历史波动率接近。

第三，20日历史波动率取不同值时，对应的未来不同期限波动率均值特征：20日历史波动率低于25%时，未来波动率均值高于20日历史波动率，且越长期限的未来波动率均值越高；20日历史波动率在30%以上但未超过40%时，未来波动率均值随历史波动率增加而增加，但低于历史波动率；20日历史波动率超过40%以后，未来各期限波动率均值均维持在40%附近不再增加。

最后，未来波动率分布标准差与均值的比值：高历史波动率环境下的比值低于低历史波动率环境下的比值。与第3条结合可以得出，低波动环境下的波动率上升，不确定性高于高波动环境下的波动率下降；即低波动环境维持的可能高于高波动环境。

接下来考虑使用历史波动率对未来波动率进行建模，以此作为不同期限的未来波动率即隐含波动率理论解的估计。使用2005年3月23日～2018年1月25日的数据，用回归的方式，以20日历史波动率、剩余交易日及相关高阶项为自变量，以不同到期期限的未来波动率作为因变量进行逐步回归，得到的最终参数及方程如表3所示，回归方程的R^2为0.91。

下面分别为回归方程的示意图。图4中，纵轴为未来的实际波动率，两个横轴分别为周期长度及20日历史波动率值。图5是回归方程在历史波动率轴上的投影，反映了回归方程中体现的未来波动率和历史波动率间的关系。

50ETF期权隐含波动率期限结构的实际值

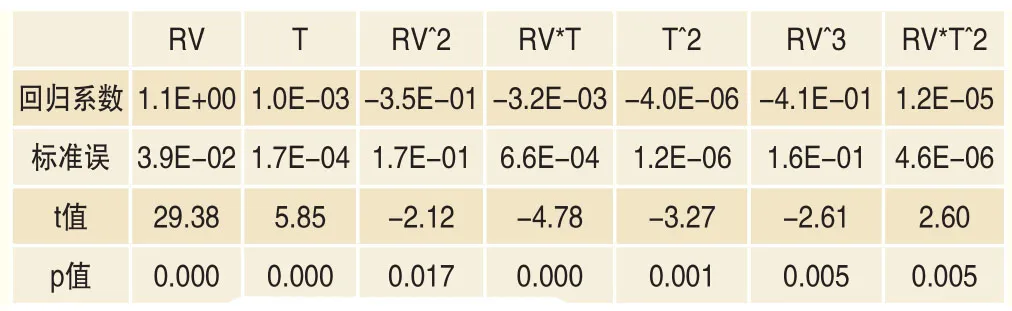
表3 回归方程的系数及显著性指标

考察50ETF期权实际的隐含波动率期限结构状况。隐含波动率是用市场的实际交易价格，按照B-S公式计算得出，体现了市场对期权的定价水平。50ETF期权自2015年2月9日上市，至2018年1月5日的四个月份平值合约隐含波动率分位点如图6所示。其中，1月IV指最邻近到期月份的平值合约隐含波动率，4月IV指最远到期月份的平值合约隐含波动率。

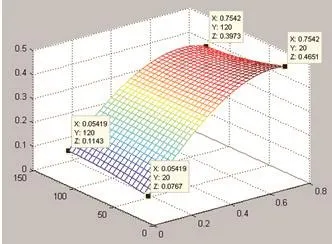
图4 未来波动率回归方程的三维示意图果

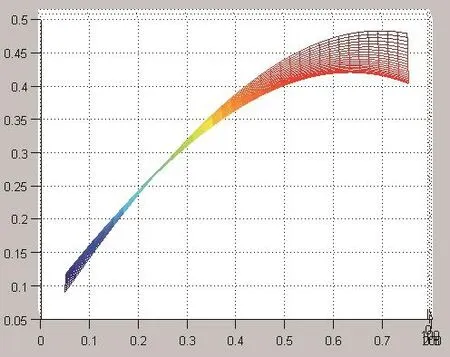
图5 未来波动率回归方程在历史波动率上的投影

四个月份的隐含波动率最大值呈现出了越临近到期合约的最大值越高的特征，最小值则基本相等且基本在2017年5月的同一时间触及。但刨除掉最大、最小这类极值后，按分位点来看4个月份合约的隐含波动率尽管同样呈现出越近月合约波动越大的特点，但范围扩大的并不十分明显；且主要是靠低波动环境下近月合约隐含波动率下降程度更高来体现、去除极值点后的高波动环境下各月隐含波动率基本一致。

由于四个月份的期权合约剩余到期时间是会随着时间变化而变化(例如，最近的一个月份，在刚换月时的剩余到期时间为一个月，在临近到期时剩余到期时间接近于零)，不能直接按1、2、3、4的方式对四个月份的合约隐含波动率进行建模。此外，如果将合约的隐含波动率数据对应到不同的剩余交易日天数上，取点过密会面临数据量不足的问题。因此，此处先将历史波动率在一定范围内，剩余到期时间在一定范围内的合约隐含波动率进行局部汇总平均，再以局部平均后的数据作为因变量进行建模。

建模的数据使用2015年2月9日～2018年1月5日的50ETF平值期权合约隐含波动率数据，自变量则与前文类似，选用历史波动率和剩余交易时间及其高阶项。通过逐步回归的方法得出回归方程如表4，此时回归系数均显著，且R^2保持在0.97的高水平。

图7分别为回归方程的示意图。其中纵轴为未来的实际波动率，两个横轴分别为周期长度及20日历史波动率值，图中的空心点为隐含波动率原始数据对应的点值。可以看到，隐含波动率的期限结构与前文提到的未来波动率期限结构是相像的：低波动率环境下隐含波动率高于历史波动率，高波动率环境下隐含波动率低于历史波动率，短期限上的隐含波动率变化范围高于长期限。

基于波动率期限结构的期权定价、交易机会分析

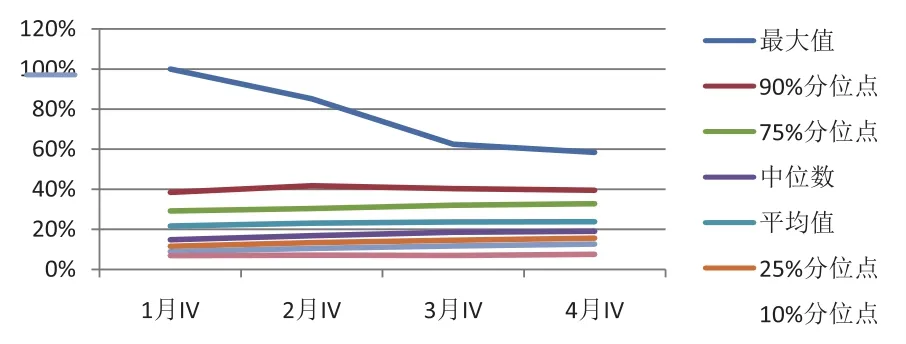
图6 四个月份平值合约隐含波动率分位点图

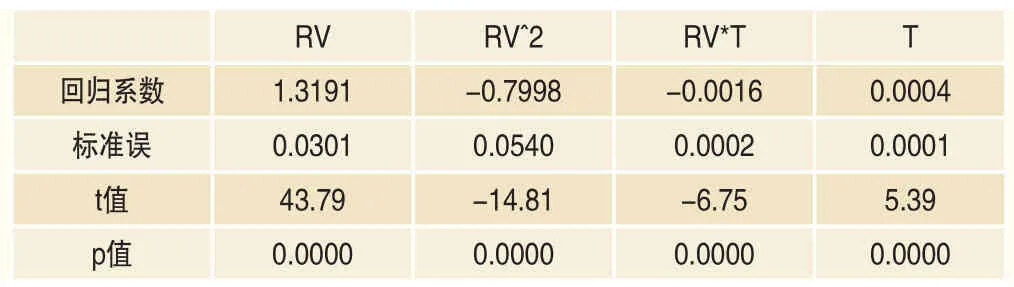
表4 隐含波动率实际值期限结构回归方程的系数及显著性指标

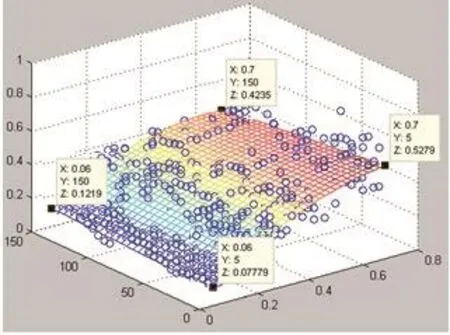
图7 隐含波动率回归方程的三维示意图

一、隐含波动率期限结构理论值、实际值的对比

前文的两个部分中，别计算了以20日历史波动率为条件，50ETF期权隐含波动率期限结构的理论值及实际值的回归方程。本部分中，首先将这两个方程进行对比，观察其区别。将两个回归方程对应的结果绘制在同一张图里，如图8所示。图中两个横轴分别为历史波动率和剩余交易日，纵轴为对应的隐含波动率理论值或实际值。

考虑到两个曲面较为接近，为便于观察，本文计算函数“理论值-实际值”，并将其三维图画出如图9。纵轴函数值大于零的部分说明理论值>实际值，隐含波动率平均意义上偏低；纵轴函数值小于零的部分说明理论值<实际值，隐含波动率平均意义上偏高。

从图9中可以发现，早2015～2018年的三年市场数据区间上，历史波动率较低时，隐含波动率平均意义上低估了未来的市场波动水平，这一特点在到期时间较远的合约上体现的更为明显；历史波动率较高时，隐含波动率平均意义上高估了未来的市场波动水平，到期时间较近的合约上体现的更为明显。

二、利用期限结构差异构建投资组合的实证分析

基于前文事实，可以考虑利用各月份的平值合约构建交易策略，捕捉期权定价偏差产生的收益。具体来说，可以在给定的实际波动率环境下，对未来不同期限的合约隐含波动率理论值进行估计，再将估计值与实际值进行对比，买入低估月份的平值合约、卖出高估月份的平值合约，通过这种方式构建基于隐含波动率实际值与理论值差异的投资组合。

图8 50ETF期权隐含波动率期限结构理论值、实际值的对比

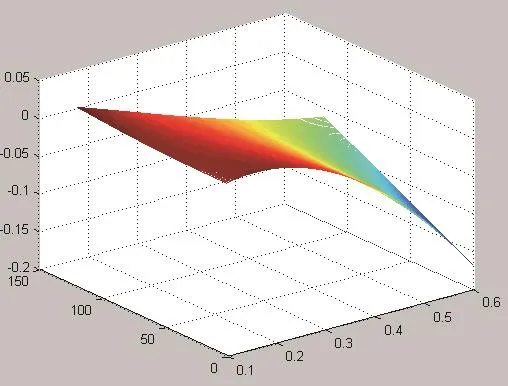
图9 50ETF期权隐含波动率期限结构理论值与实际值的差值

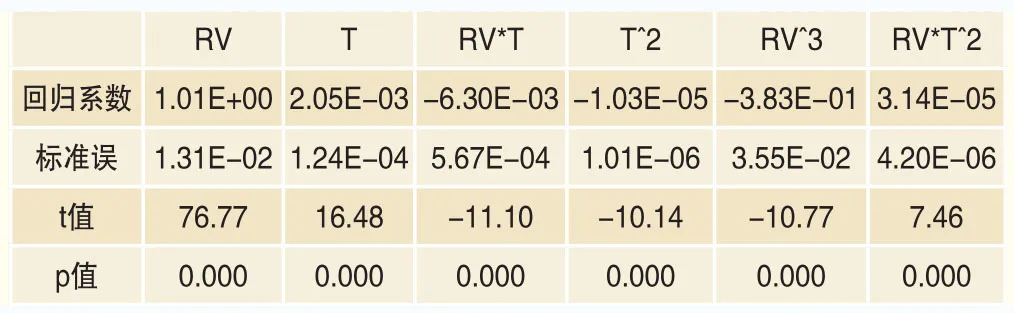
表5 隐含波动率理论值回归方程的系数及显著性指标

本部分中，为避免使用未来数据，本文使用2005年3月23日～2015年2月6日的数据估计期限结构理论方程并保持方程不变，再将2015年2月9日～2018年4月26日上各交易日时点上的数据代入期限结构方程，计算得到各时点上的隐含波动率期限结构理论值。最后，对比隐含波动率实际值与理论值的差异，构建投资组合。

首先，计算回归方程。根据前述说明，利用2005年3月23日～2015年2月6日区间上的数据计算得到的回归方程如表5所示。

接下来，根据上述回归方程设定组合并进行回测，具体步骤如下：

1.计算各月持仓多空方向

每个交易日，将历史波动率和合约剩余到期时间代入回归方程，计算得到四个月份的理论波动率，再将理论波动率和四个月份平值合约的隐含波动率对比，得出四个月份分别的多空信号。

2.计算各月总持仓数量

每个月份的合约均以平值合约建仓，认购及认沽总和不超过60张。持有的具体张数按隐含波动率与理论波动率的差值设定，二者的差异在10%以内时不持仓，差值超过30%时持有设定的最高数量(此处为60张)，差值在10～30%之间时持有数量线性递增取整。

3.计算各月认购、认沽期权持仓数量

计算出各月份总持仓数量后，分别根据该月份的认购、认沽期权的Delta值，算出使该月总Delta为零的合约张数，并四舍五入取整得到认购、认沽期权合约的持仓数量。

4.计算策略收益

按照每个交易日的信号得出次日的合约持仓，并使用收盘价计算出次日的收益，累计得到策略的最终收益。

图10是上述策略最终得到的累计收益走势，其中按“手续费+摩擦成本”为5元、10元、20元三种情况进行了分别测算。

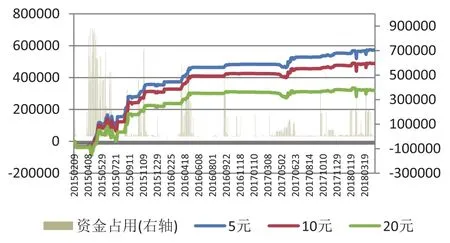
图10 不同交易成本下的组合累计收益走势

表6中是组合收益的相关统计数据。其中，收益率部分均按照100万元的初始资金进行测算(分年份的收益测算中，每年初均按100万初始资金测算，因此分年度的收益率累积不等于全时间段的总收益率)，事实上在2015年2月9日～2018年4月27日的区间中，组合的平均资金占用仅为8.5万元，资金占用峰值为88.7万元，100万元的初始资金较充分，而且大部分时间中资金处于闲置状态(此处不考虑闲置资金带来的利息收入)。

从收益角度来看，组合在2015年的收益较佳，2016年之后随着市场日渐完善、波动低迷交易机会变少，收益出现下降。考虑到组合平均意义上占用资金较少，闲置资金会对收益率产生不利影响，测算了另一种模式的累计收益率：初始资金改为20万元，每个交易日中不足部分的资金按照“临时资金”进行计算、按年化10%的利率和占用时间扣除收益，空闲的资金则按3%的利率计算利息。此时按10元交易成本计算的组合累计净值及各年度净值如图11所示，可以看到此时收益率在逐年下降仍然非常可观(2015年、2016年、2017年的全年收益率和2018年至4.27的年化收益率分别为157%、61%、29%和24%)。

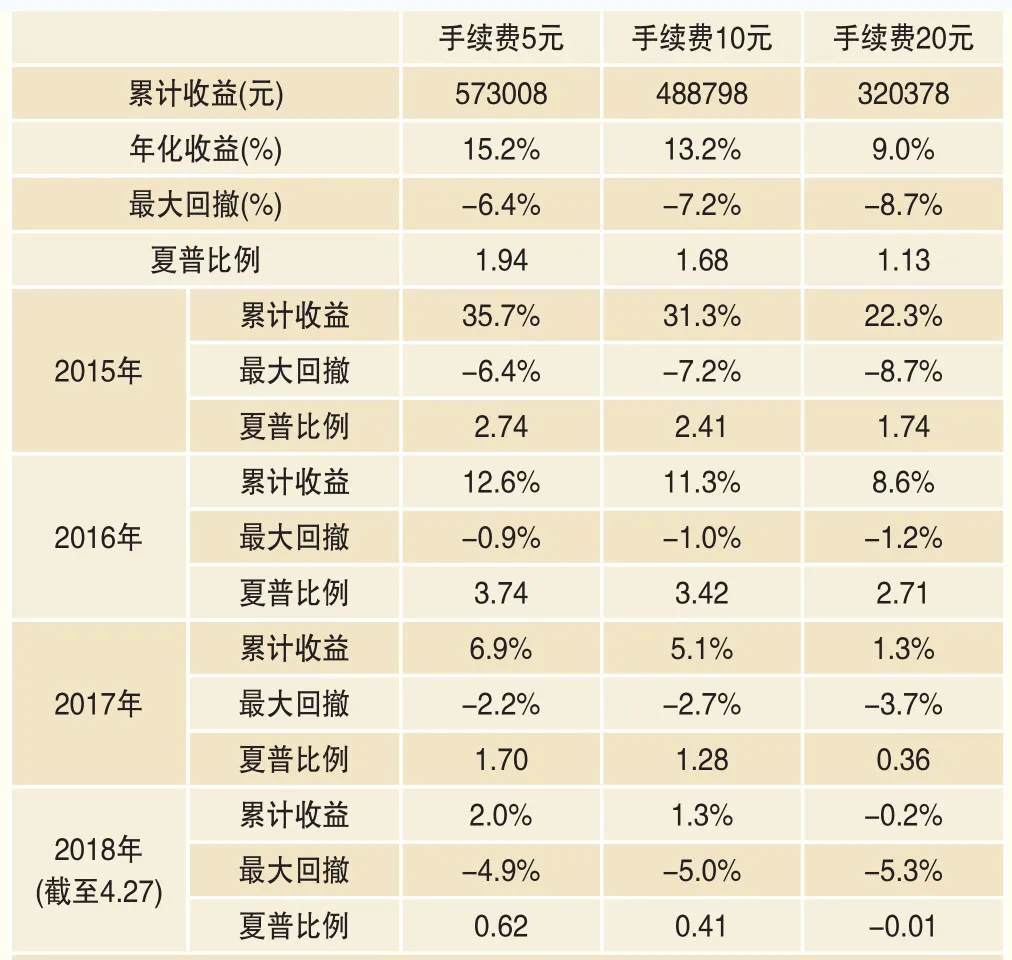
表6 整体及分年份的若干统计指标

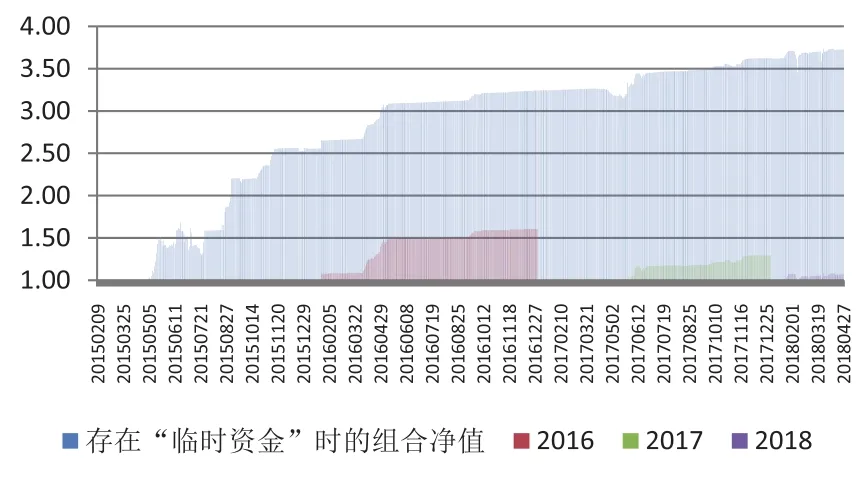
图11 存在“临时资金”时的组合累计净值

主要结论与建议

从2015年2月9日上交所50ETF期权正式上线至今已接近4年，期间市场中新的股票、商品期权标的逐渐增加，未来新的期权标的品种也将逐步问世。在此背景下，了解标的收益特征对期权隐含波动率曲面的影响，对探索期权的定价和价格发现机制、指导实际的期权交易均具备重要的价值。本文以历史波动率作为条件变量，分析了不同历史波动率环境下的未来波动率、隐含波动率分布特征，并基于二者的差异进行了交易策略的实证分析，结论如下：

(1)50ETF的实际波动率和50ETF期权隐含波动率均体现出了聚集效应、均值回复等普遍认可的波动率特征；

(2)历史波动率对未来实际波动率的期限结构和隐含波动率期限结构的拟合效果良好，回归的R^2分别达到了0.91和0.97；

(3)从过去三年平均意义上来看，实际波动率较低时，隐含波动率低估了未来市场波动水平，期限较远的合约上体现的更为明显；实际波动率较高时，隐含波动率高估了未来市场波动水平，到期时间较近的合约上体现的更为明显；

(4)基于理论波动率和隐含波动率的期限结构差异，可以构建Delta中性的组合捕捉收益。在2015.2～2018.4的时间区间上，如果基于资金峰值加安全垫作为初始资金、不考虑利息收入、按交易成本10元计算则年化收益为13%；

(5)2016年之后，期权市场定价效率明显提升。受此影响，来源于期限结构的交易策略收益呈逐年下降走势。但考虑到策略资金占用的峰值远高于均值，如果在资金占用较多时存在可临时借用的资金(有方便快速借入的资金，或是组合仅作为多策略中的一部分)，则策略收益在逐年下降后仍然非常可观。