盘点抛物线的焦点弦问题

■甘肃省秦安县第二中学 罗文军

设直线l经过抛物线C:y2=2p x(p＞)的焦点F,且与抛物线C交于A、B两点(直线A B的倾斜角为α),设A(x1,y1),B(x2,y2),O为坐标原点,准线方程为:x=,则关于抛物线C的焦点弦有以下九条常用的性质:

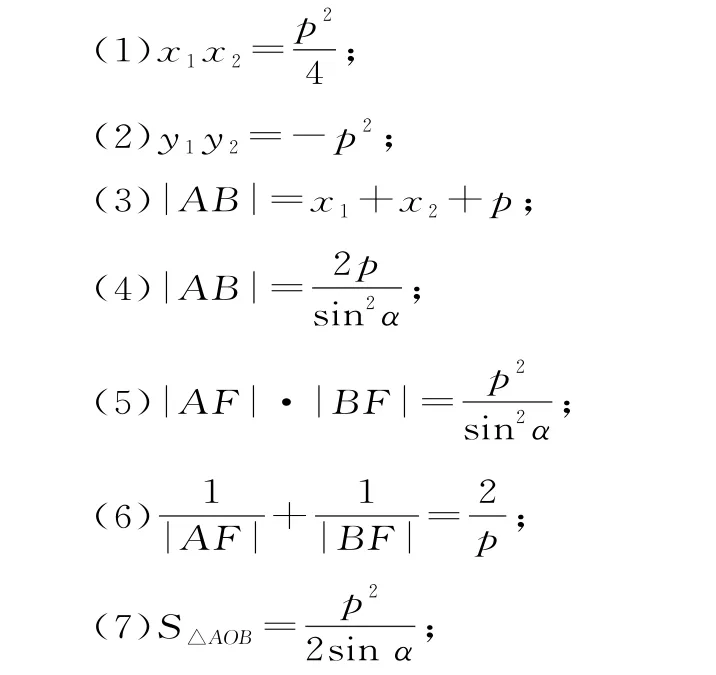
(8)以A B为直径的圆与准线相切;

(9)以A F、B F为直径的圆都与y轴相切。

以下运用上面焦点弦的性质来破解一些比较经典的焦点弦问题。

例1(2018年高考全国Ⅱ卷理科第9题)设抛物线C:y2=4x的焦点为F,过F且斜率为k(k＞0)的直线l与抛物线C交于、B两点,且|A B|=8。

(1)求直线l的方程;

(2)求过点A、B且与抛物线C的准线相切的圆的方程。

解析:(1)解法1:由题意得点F的坐标为(1,0),直线l的方程为y=k(x-1)(k＞)。

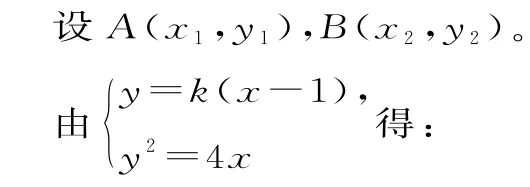
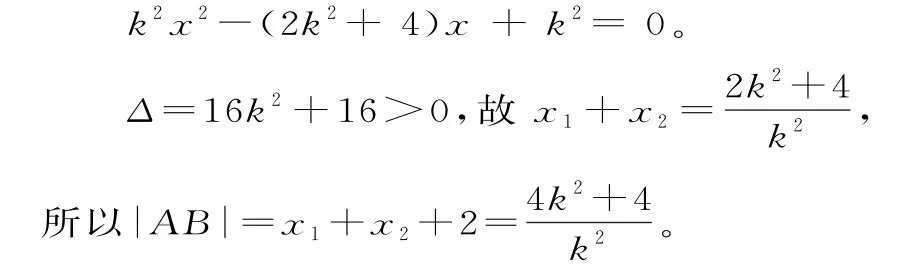
所以直线l的方程为x-y-1=0。

(2)由(1)知,直线l的方程为y=x-1。

设A B的中点的坐标为(x0,y0),由中点坐标公式可得,

所以y0=x0-1=2,直线A B的垂直平分线的方程为y=-x+5。

要求的圆的圆心一定在直线y=-x+5上,设圆心坐标为(x1,-x1+5),则(x1+1)2=16+(x1-3)2+(-x1+5-2)2,解得x1=3或x1=11。所以圆心坐标为(3,2),半径为4,或圆心坐标为(11,-6),半径为12。

要求的圆的方程为(x-3)2+(y-2)2=16或(x-11)2+(y+6)2=144。

评注:第一问中的解法1将直线方程与抛物线方程联立消元后,再运用了抛物线的焦点弦公式,最后解出k的值,得出直线的方程。解法2运用了弦长公式这个公式只适用于抛物线y2=2p x(p＞0)的焦点弦问题。第二问要求圆的方程,首先要确定圆心坐标与半径,线段A B为所求圆的弦,根据弦A B的垂直平分线经过圆心,再根据垂径定理,直线与圆相交时,|A B|=,其中r为圆的半径,d为圆心到直线的距离,解方程可得出圆心坐标和半径长。

例2设F为抛物线C:y2=4x的焦点,过F且倾斜角为30°的直线交抛物线C于A、B两点,O为坐标原点,则△A O B的面积为____。

解析:由题设可得,p=2,所以S△AOB=

因此,△A O B的面积为4。

评注:本题属于小题,可直接运用抛物线的焦点弦的性质,得出所求三角形的面积,思路简单明了。

例3设抛物线C:y2=4x的焦点为F,直线l过F且与抛物线C交于A、B两点,若|A F|=(3+22)|B F|,则直线l的方程为____。

解析:设直线A B的倾斜角为θ,由题意知

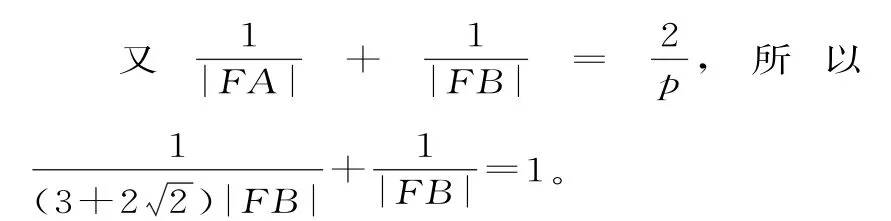
所以k=t a nθ=±1,直线l的方程为y=x-1或y=-x+1。

评注:本题运用了抛物线焦点弦的两条性质,通过解方程最终得出直线的斜率,以及直线的方程。

例4(2018年全国Ⅲ卷理科第16题)已知点M(-1,1)和抛物线C:y2=4x,过抛物线C的焦点且斜率为k的直线与抛物线C交于A,B两点。若∠AMB=90°,则k=____。

解析:记抛物线的焦点为F,由题设可得

因为∠AMB=90°,则以A B为直径的圆与准线相切于点M。

评注:本题属于小题,可直接运用抛物线性质的二级结论:以抛物线的焦点弦为直径的圆与抛物线的准线相切,解法简单明了,减少了运算量。

例5设抛物线C:y2=2p x(p＞0)的焦点为F,点E在抛物线C上,|E F|=4,若以E F为直径的圆过点,则抛物线C的方程为____。

解析:由抛物线的性质可得,以E F为直径的圆与y轴相切,且切点坐标为因为

所以抛物线C的方程为y2=4x或y2=1 2x。

评注:本题的解答中先运用了抛物线的焦点弦性质,再通过解一元二次方程,最终得出抛物线的方程,减少了运算量。

例6已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与抛物线C交于A,B两点,直线l2与抛物线C交于D,E两点,则以线段A B和线段D E为两条对角线的四边形的面积的最小值为____。

解析:设直线l1的倾斜角为α,则|A B|

所以,以线段A B和线段D E为两条对角线的四边形的面积为:

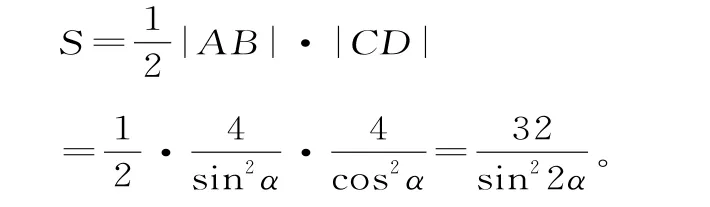
当s i n22α=1时,即时,所求四边形的面积取得最小值32。

评注:本题设出直线的倾斜角,先运用了抛物线的焦点弦公式,再利用三角函数的知识解出所求四边形的最小面积。

例7已知F为抛物线C:y2=4x的焦点,E为其准线与x轴的交点,过F的直线交抛物线C于A,B两点,M为线段A B的中点,且

解析:由题设可知E(-1,0),F(1,0),设A(x1,y1),B(x2,y2)。

设直线A B的斜率为k,则直线A B的方程为y=k(x-1)。

由焦点弦公式知|A B|=x1+x2+p=2+2+2=6。

评注:先设出两个交点的坐标,运用中点坐标公式,再将直线方程和抛物线方程联立,利用设而不求的思想,得出两根之和,建立关于k的方程,解出k2,运用抛物线的焦点弦公式和整体代换的思想,最终得出抛物线的焦点弦长。