智能交通流仿真及通行质量影响因素分析∗

陈颢天 尹超群 贺明峰

（1.大连理工大学海洋科学与技术学院 大连 116024）（2.大连理工大学文法学院 大连 116024）（3.大连理工大学创新创业学院 大连 116024）

1 引言

在现今对于道路通行效率的研究中，影响通行效率的因素随科技发展的增加而使得研究的复杂程度大大增高。在原本普通车辆模型的基础上，又增添了智能车、超速车、关卡、路段宽度以及路段长度变化因素对于道路通行效率的影响。为具体观测与预测多种因素影响下道路通行效率的变化，本文主要采用元胞自动机模型对于各类车辆运行规则建模，综合考虑且分别控制一些因素后，用计算机仿真得出通行效率的变化，并以此分析产生此类变化的原因，由此得出某因素对于通行效率的直观影响。

元胞自动机是一种离散的非线性动力系统模型［1］，标准的元胞自动机可视为由一个元胞空间和定义于该空间的变化函数组成［2］，它用简单的规则表达一般类型的规律，在计算机上模拟复杂的自然现象和社会现象。一些学者利用元胞自动机的理论构建交通流模型，模拟车辆运行，取得了较好的应用效果。

王永明等在模型中根据驾驶人对实际路况的不同判断，相应地改变车辆行驶规则中换道规则，并对不同交通流密度下的仿真分析，得出一般的换道规则［3］；程晓明等通过对NaSch模型中随机规则的研究，提出车辆的减速概率会随车流速度变化而变化的VDR模型，仿真两模型的时空分布图，得出随机规则是模拟交通车流中许多非线性现象（例如启动-停车波）的主要规则［4］；杨洪礼等对于有超车规则的交通模型建立进行了研究，提出了效率及安全评价指标、微观规则、宏观概率设计、评价方法的选取、交通规则的设计以及仿真实验等方面的建设思考［5］；丁建勋等利用驾驶人的记忆效应和当前交通环境动态调整随机慢化概率，得到一个改进的交通流元胞自动机模型，并且验证引入记忆效应可以提升道路的平均速度和车流量［6］；郑亮等将与安全间距有关的驾驶员的行为作用机理引入CA模型，得出了稳定性更高、更接近实测数据以及堵塞消溶效率更高的ACA模型［7］；卫妮娜等通过Matlab数值模拟仿真得到车流量和车流密度之间的关系曲线，并分析了两种交通规则优化下的车流量情况［8］；Tao Chongyuan等应用多车道元胞自动机模型验证“除超车外靠右行”这一交通规则的有效性［9］；文献［10～11］中也提出了阻塞-转移和元胞遗传算法演化的改进交通规则。

此外，一些学者使用元胞自动机仿真交通流之外的场景，亦取得了较好的应用效果。丁元春等利用元胞自动机模型研究楼梯及电梯-楼梯耦合情况下的疏散，并讨论恐慌心理及超越行为对整体疏散的影响［12］；于全魁等对地震作用下框架结构倒塌造成的人员伤亡进行分析，并用元胞自动机模型初步研究开发了地震时建筑物中人员逃生过程模拟及伤亡预测系统［13］；Wang Xuehua等应用元胞自动机综合分析易燃物、风力、温度及地势等影响因素对森林火灾蔓延形式的影响，提出森林火灾预测系统［14］。由此可见，元胞自动机模型规则制定是决定其应用是否成功的决定因素。

现有文献和上述学者们的研究成果中，有对元胞自动机NS规则中随机慢化规则的改进［15］，目的是为了使得元胞自动机模型更加的贴近实际，也有对于驾驶心理如何影响换道概率的研究，进而提高道路的利用率［16］，此外还有诸多对于随机过程的研究［17］，上述研究基本都是针对一般交通流模型。本文通过分析道路行驶中的动态情况及多种影响因素［18～20］，将元胞自动机模型应用于一个综合驶入流量、智能与非智能驾驶车辆、车辆超速情况以及交通收费窗口设置等多种因数的场景中，构建了相应的复杂智能交通流的模型，并在不同条件下进行了仿真。

2 智能交通流模型构建

本文依据当今车辆对道路的影响能力把行驶车辆分为普通车、智能车两类。本文智能车为全工况无人驾驶完全自动控制车辆：可全程检测交通环境，能够实现所有的驾驶目标，驾驶员只需提供目的地或者输入导航信息，在任何时候都不需要对车辆进行操控。

本文以交通情况复杂的高速公路中夹带收费亭路段作为研究路段（其中车道数量为R，收费亭车道数量为T）并将其划分成l1行l2列的元胞矩阵，其中每一个元胞代表的实际长宽皆相同且每一条车道宽度皆相同；模型中收费亭的数量多于车道数、都正常工作并且无外界因素（暴雨、大雾、路面结冰等）影响。

普通车及超速车的运行规则如下。

1）速度调整规则

调整规则：考虑驾驶人的主观意愿，在满足调整的客观条件时，驾驶人主观上可以最终决定是否调整。假定主观上决定调整的驾驶人与驾驶人总量之比为p1，当前时刻某一特定车辆速度为v，当前时刻产生的随机概率为p，则该特定车辆速度依据加速规则具体变化如下所示：

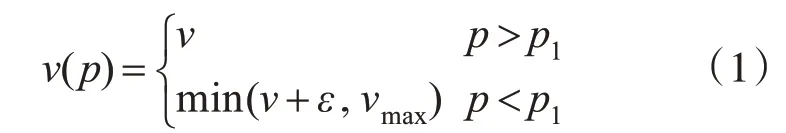
其中，ε取值如下：

2）换道规则

驾驶人在行驶时先判断前方一个元胞处有无车辆，若有车辆、当前时刻生成的随机概率值小于决定换道驾驶人占比p2、车辆任意一侧无车辆且该侧前方一个元胞内亦无车辆，则车辆向该侧换道成功。

3）碰撞条件

当车辆换道完毕前进时，车速v减去最大减速度vmax后依然大于车头间距h时则与前车发生碰撞，且碰撞之后两车所处元胞变为不可通过元胞。易分析得出仅超速车可产生碰撞，碰撞条件数学表达如下：

智能车的运行规则如下：

1）基本规则

根据定义，本模型中智能车加速减速以与前车保持安全车头间距为依据调整，即前方车速为v时，车头间距保持h+v-2＞0。

2）换道规则

本文结合智能车的不同运行功能给出两种换道规则。

换道规则1：使用前提为智能车搭载测速系统。当检测得前方车速为0且h-2＜0时，执行换道规则，若无法换道，则无间隔停在车辆后方。

第二种为换道规则2，使用前提为智能车具备联网读取路段车流情况的能力。在至少三车道情况下，智能车判断目前所处车道与左右车道中平均车流速度的大小，其中单车道平均车流速度数值计算依据微观交通流粒子模型概念，但最大不得超过vmax：

其中L为车道长度，N为车道中车辆数。

若某一时刻，车辆所在车道中车流速度小于两侧道路中任意一侧的车流速度，则判断车辆两侧有无车辆，若满足任意一侧没有车辆，则车辆换道成功。

3 程序设计与仿真分析

程序采用Matlab进行编写，由多个子程序协同运行得出结果，并进行分析得出结论。

3.1 程序设计

本文取车道数量为4，收费亭车道数量为8。定义窗口服务率S为单位时间内可服务的车辆数，并取S=0.8。

在引入车辆子程序中，本文假设车辆的到达服从泊松分布，即单位时间步长内到达的车辆数为n的概率为

依据某一时刻产生的到达车辆随机数，再与空车道数比较取最小值，即可得到某时刻应当到达的车辆。其中λ在本模型中为车辆到达率。

3.1.1 换道规则的程序设计

具体执行换道规则程序过程中，找寻车辆命令与判断车辆两侧位置是否为空命令皆存在先后顺序性，不符合实际情况。实际中车辆运行呈无序性，且车辆换道方向呈随机性。因此，本文提供一种改进方案：先将所有车辆依次找出，打乱顺序后再依次进行判断。判断时，对于产生换道需求的车辆，先判断左侧是否为空的概率与先判断右侧的概率各占50%，某侧判断换道条件一旦成立，将直接进行换道，不再判断另一侧情况。

3.1.2 速度调整规则在考虑最低限速时的程序设计

若直接限定大于0的最低速度而对模型不作任何更改，加速规则与最低限速之间将产生冲突。以无收费道口公路为例，若程序不对因防止碰撞而速度骤减的车辆以及随机被挑选减速的车辆加以区分，依照规则，程序判断完车速不可大于两车之间间隙，将车速减至低于x防止碰撞，在运行至限定最低速度处时，使得原本速度低于x的车辆重新加速至x，不仅引发碰撞，甚至导致仿真发生混乱。

本文提供的解决方案为：以不产生碰撞为最优先前提，在程序执行最低速度规则前先对车辆执行规则后的车速进行判断，若判断得出执行规则后将发生碰撞，则程序将放弃执行最低速度规则。

3.1.3 仿真结果

为更加清晰地分别观测智能车占比与超速车占比对于交通状况的影响，采取对比仅含普通车路段、普通车智能车混合运行路段以及普通车超速车混合运行路段，控制三者的入车流量、入车位置以及道路形状完全一致，以完成对两者的后续评价以及直观观测对比。先后取l1=101、l2=10与l1=1000、l2=10，迭代4000次，结果见图1。

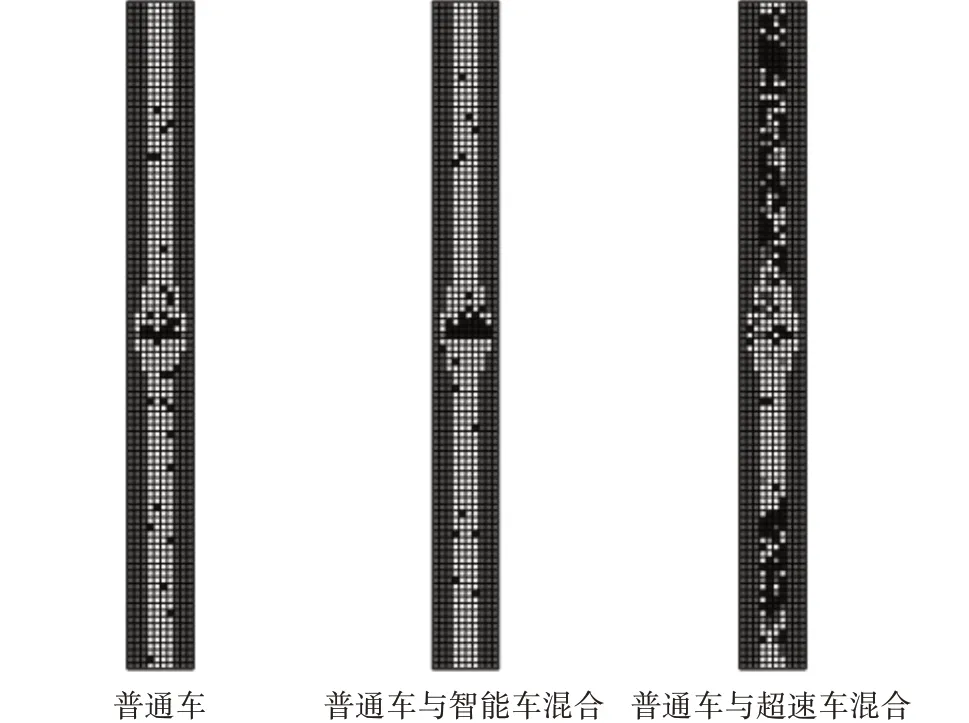
图1 三种情况下仿真过程快照图

从图1可见，智能车的加入在较小车流量时对于道路状况直观上的改变不很明显，而超速车的加入大大增加了路段中的事故发生率，事故导致道路拥堵明显，通行能力显著降低。

3.2 仿真分析

3.2.1 基于仿真结果的换道规则选取与讨论

本文对智能车的两种换道规则进行仿真模拟后，令道路长度为1000，可得出长路段下换道次数与智能车占比关系曲线如图2所示。

图2 换道规则1下智能车占比与换道次数关系

而使用换道规则2时关系曲线如图3所示。

图3 换道规则2下智能车占比与换道次数关系

由图3可观测得，当智能车占比增加至92%以上时，换道规则2下换道次数降低迅速，最后降至低于100。其原因为道路长度增加使得各条道路中车流速度增大，当智能车达较高比例后，遵守换道规则2的车辆占绝大多数，由公式可知邻近车道中车流速度接近，换道前提条件极难达成。

综合两图可知，道路长度增长可使得车辆换道次数降低，即事故发生率会降低，也从侧面证明了车辆与车辆之间距离变宽，道路中的车辆密度减少，为后文研究打下理论基础。

依据分析对比结果，换道规则1较2而言更加稳定，平均换道次数更少，而在实际路段中换道次数更少亦代表事故发生率更低，故换道规则1更加适合作为智能车运行所依据的规则。

3.2.2 分析智能车比例变化对于交通状况的影响

本文将每一辆车量通过整个路段所用时间的平均值定义为平均时间，以此作为衡量道路运行效率的指标。

1）换道规则下的影响分析

当车辆不发生换道，且道路中没有智能车加入时，为直观分析道路入口平均车流密度与车辆所用平均时间的关系，作平均时间随车辆到达率λ变化曲线如图4所示。

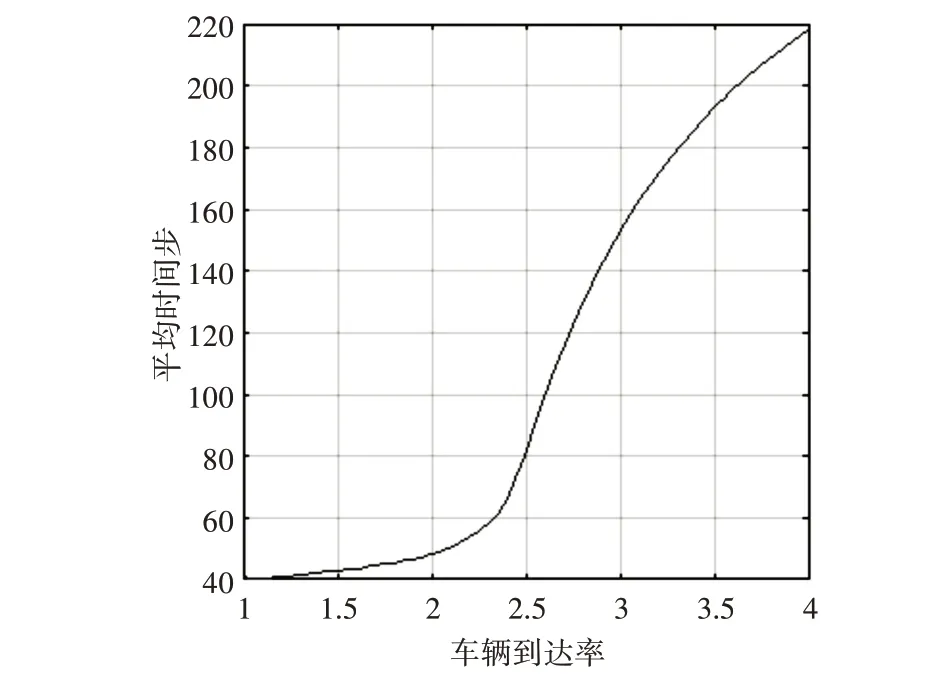
图4 无换道规则下入车流量与平均时间关系曲线

2）换道规则1下的影响分析

在模型构建部分中对于最高等级的智能车有其定义，本文用数学语言表达定义后进行多次重复仿真以去除结果的偶然性。

控制入口平均车流密度不变（限定车辆到达率为4），在设定道路长度为101时，分析换道规则1下智能车比例对于交通状况的影响，得出如图5关系曲线。

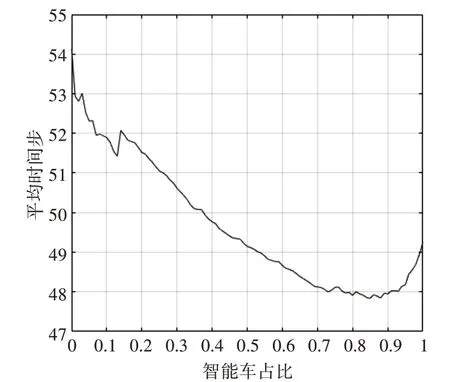
图5 道路长度101时智能车占比对平均时间的影响

如图5关系曲线所示，智能车比例在0%～80%时，对于交通流优化效果单调增加，在80%～90%之间时，对于交通流的优化效果达到最佳，在90%～100%时优化效果逐渐单调减少。从宏观角度分析智能车对于交通流的影响，由于智能车需要与前车保持间距，一方面其疏通了道路，使得拥堵减少，但另一方面，车头间距以及换道规则的存在使得车辆的密度减小，道路的运行能力则会有所降低，两者变化之间存在一个平衡点，即为图中最值点产生的原因。

而将道路长度增长至1000时，依然限定λ值为4，同样条件所得关系曲线则如图6所示。

图6 道路长度1000时智能车占比对平均时间的影响

由图6可知，当道路长度被大幅度拓宽时，追踪车速矩阵可知路段中的车辆车速将有更多时间与几率提升至最高，由前文换道规则部分研究结果可证明道路长度增加使得路段中的车辆密度减少，因此智能车的引入对于密度本就小的路段而言将不再存在负面影响，故智能车占比越高，道路运行效率则越高。

综合对比智能车对道路运行效率的影响，可得出结论：智能车的适当引入对于道路交通状况可达到一定程度的改善作用；并且在80%以下区间内引入智能车时道路状况都是随智能车占比增加而得到改善的。

3）换道规则2下的影响分析

控制入口平均车流密度不变（限定车辆到达率为4），在设定道路长度为101时，分析换道规则2下智能车比率对于交通状况的影响，得出如图7关系曲线。

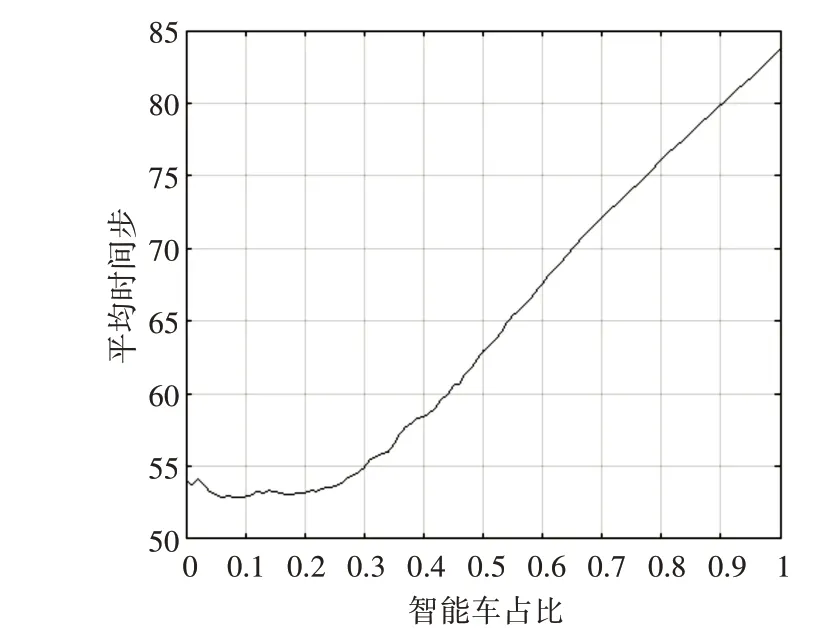
图7 道路长度101时智能车占比对平均时间的影响

如图7关系曲线所示，在以换道规则2为基本规则运行时，智能车比例的增加使得平均时间步呈增长趋势，道路的通行能力降低。

而将道路长度增长至1000时，同样条件下所得关系曲线则如图8所示。

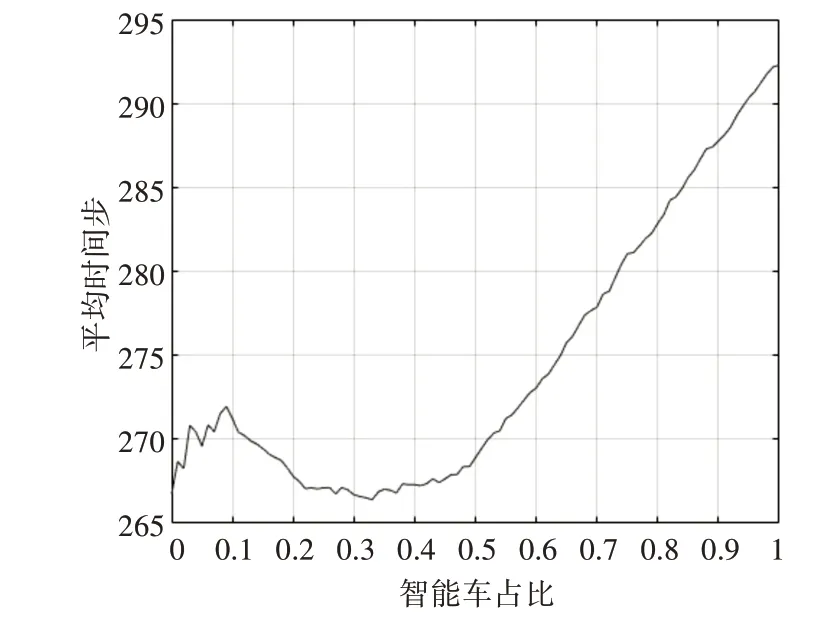
图8 道路长度1000时智能车占比对平均时间的影响

由图8可知，当道路长度拓宽后道路中车辆密度整体较小时，关系曲线出现了两次极值。可知在换道规则2下智能车比例在30%～35%之间时，智能车对于道路效率的优化效果达到最好。然而曲线整体高于换道规则1中相同条件下曲线。

对比两种换道规则下智能车占比对平均时间影响，综合比较短路段与长路段研究结果，印证前文基于仿真结果的换道规则选取部分中所讨论得出最终结果是正确的，换道规则1更加有利于道路运输效率的提高。

4 结语

本智能交通流模型的规则制定中不仅引入驾驶人可能超速行驶的主观因素，还适应智能车发展迅速的客观趋势，考虑智能和非智能车辆比例，增加了该模型的普适性。依据仿真所得数据进行对比分析，结果表明：该模型可以有效描述智能交通流，直观观测出不同比例下车流对于交通的影响，亦可追踪某一具体车辆元胞从微观上分析车流情况。