基于改进遗传算法的柔性车间调度问题的研究∗

曹 睿 侯向盼 金巳婷

（1.大连交通大学 大连 116028）（2.中车青岛四方机车车辆股份有限公司 青岛 266031）（3.沈阳铁路局通信段 沈阳 110001）

1 引言

在柔性车间调度问题中，每一个部件中的每一道工序不止固定在一台机器上，可根据具体情况选择不同的机器加工，并且不同机器加工的时间有所不同，与传统的车间调度相比更具有灵活性［1］。本次设计利用改进的遗传算法对柔性车间部件生产完工最大时间最短作为性能指标，确立为目标函数，对种群初始化和交叉变异部分进行改进，提高全局的搜索效率，通过实例说明改进的遗传算法对柔性车间的调度优化问题有所改善［2］。

2 柔性作业车间调度问题及参数描述

多目标柔性作业车间调度是指生产车间中在m台设备｛M1，…Mn｝上加工n个工件｛1,…N｝，每个工件包含ni个事先确定加工顺序的工序，每道工序可以在多台设备上加工，每道工序不同的机器加工加工时间有所不同。本文主要考虑最大完工时间最短的性能指标［3］，其目标函数的建立如下：

调度目标是为每道工序选择合适的机器、确定每台机器上各个工件工序的最佳加工顺序以及开工时间，使得工件的最大生产周期最短。除此之外，在工件加工过程中还需要满足下面的几个约束条件：1）工件i在机器j上的加工时间需要大于0；2）工件i的加工时间必须在规定时间范围内；3）对于特定的工件i，机器j必须先于机器m对其进行加工；4）任意工件的加工过程必须是连续封闭的［15］。

一个包含3个工件、5台机器的FJSP的问题描述如表1所示。

表1 3个工件、5台机器的柔性车间调度问题

3 算法设计

3.1 染色体编码

柔性作业车间调度编码由两部分组成：一部分是基于机器分配的编码，对应机器选择子问题，确定所选择的加工机器；另一部分是基于工序的编码，对应工序先后加工的排序子问题，确定工序的先后加工顺序［4］。

以3×5柔性车间调度问题为例说明，第一层对工序顺序进行编码得到的加工序列：O11→O31→O21→O12→O22→O32→O23→O13，第二层编码是基于机器的编码可以获得工序对应的加工机器序列：M1→M3→M2→M3→M4→M5→M1→M2。

第一部分是所有工件加工时间

第二部分是机器在加工工件时的准备时间

表示上一工件结束加工时的拖延时间

3.2 种群初始化

根据车间的具体情况，在M个可用机器中选择k台性能优良、加工时间相对较短的机器作为一个小规模的初始群体，求出这k台机器的平均加工时间tA，将剩下的( M-K)台机器的加工时间tP与tA相比较，为保证初始种群的数量，根据实际情况设置一个tP与tA的差异范围Q，即若 |tA-tP|∈Q，则保留，否则，该机器淘汰，这样可以保证初始种群的适应度，提高搜索效率。流程图如图1。

图1 初始化流程图

3.3 适应值函数

在遗传算法中，适应度越高，被选择的几率就越大［8］。在本次设计中，将适应度函数表示成目标函数倒数的形式，即

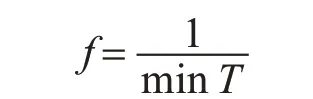
其中min T表示目标函数，即最小生产周期，这样，当生产周期T最小时，适应度函数值最大，就表示这条加工路线的时间最短［6］。

3.4 选择操作

首先将种群内个体按适应度大小从高至低排序，利用最优个体保存法将父代中的最优个体即适应度最高的个体直接保留进入到下一代［7］。

3.5 交叉操作

针对FJSP本文提出了两种交叉操作，第一种是POX交叉操作［11］，用于染色体中工序的加工顺序的交叉；第二种是节点交叉操作用于染色体工序分配的机器的交叉。

工序染色体的交叉过程：

P1和P2为父代，交叉后产生子代C1和C2。首先将所有的工件分成两个集合J1和J2，子一代的染色体C1/C2继承父代中J1/J2内的工件对应的基因，子一代剩余的部分基因由父代剔除了C1/C2中剩余的基因来补充［9］。

机器染色体的交叉过程：

采用节点交叉法，即将整个染色体的基因串均匀分成三部分，这样在染色体上就会产生两个基因位点，选取每个基因位点两侧相邻的字符组成一个基因段进行交叉，这样既避免了基因交叉分布的不均匀性，又能提高全局搜索效率［14］。

3.6 变异操作

第一部分变异时，在机器染色体基因串中随机选择一个位置，在此工序的机器集中随机选择一个与它不相等的整数，替换当前的基因［10］，这样确保得到的解是可行解。

第二部分采用相邻交换变异法，以一定的概率随机选取两个位置的相邻基因串进行交换，与交叉操作类似［13］。

3.7 终止条件

本次设计中，根据实际情况，采用设置最大迭代次数的方式来终止算法的执行［12］。

4 仿真结果分析

表2是以6×6的柔性作业车间各工件不同工序加工时间表为例。

表2 6×6柔性作业车间各工件不同工序加工时间

图2 问题收敛曲线图

图3 GA-A迭代曲线图

图4 GA-B迭代曲线图

5 结语

通过图2两种遗传算法GA-A与GA-B适应度函数的收敛曲线图可知，本次所设计的遗传算法相对于传统算法而言，能够快速收敛，迅速搜索到最优解，且能够克服早熟现象，搜索有效稳定；通过对

遗传算法运行的参数设置如下：种群初始规模S=60，交叉概率Pc=0.8，变异概率Pm=0.01，最大进化代数X=50。将最小生产周期作为适应度函数，并按上述所设置的控制参数，分别基于传统遗传算法（GA-A）与本次所设计的遗传算法（GA-B）对上述实例进行仿真，经过Matlab多次运行仿真后，仿真结果如图2～4所示。比分析图3GA-A与图4GA-B两种算法的迭代仿真图像可知，本次所设计的遗传算法GA-B在30代以内便可收敛至最优解，而传统遗传算法GA-A迭代至70代时才收敛至最优解，说明算法GA-B在解决车间实际生产调度问题时更加有效。