万有引力搜索算法的Web服务选择∗

袁 博 马 力

（西安邮电大学 西安 710061）

1 引言

由于受到自然界群体现象的启发，在过去的几十年里，研究人员提出了多种群体智能算法，如人工蚁群算法［1］，粒子群算法［2］等，它们一般通过模拟生物种群或者自然物体的客观规律来达到寻找最优值的目的。

万有引力搜索算法［3］（Gravitational Search Algorithm，GSA）在2009年首次由伊朗克曼大学的教授Esmat Rashedi等提出。万有引力搜索算法是一种新的启发式智能优化算法，它是在牛顿万有引力定律［4］及粒子间的相互作用的基础上被提出的。

近几年，有关万有引力搜索算法一直是人们研究的重点，文献［5］用万有引力搜索算法来解决约束优化问题。为防止出现早熟现象，文献［6］将混沌变异添加到万有引力搜索算法中。为提高分类问题的精确度，文献［7］提出了将GSA与SVM相结合的模型。

但GSA算法也一定的缺点：算法停滞、早熟现象以及局部最优问题，因此本文利用万有引力搜索算法和粒子群算法相结合，并对粒子运动速度方程方程进行改进，结合实验，所改进的算法具有较好的性能。

2 万有引力搜索算法

2.1 万有引力搜索算法原理

在GSA中，惯性质量大的粒子比惯性质量小的粒子运动得慢，所以物质都朝着惯性质量大的粒子运动。粒子的位置就是问题的解，当算法满足结束的条件时，拥有最大惯性质量的粒子它的位置就代表问题的最优解。

在GSA中，设参与搜索的粒子组成的系统是独立的，是遵循万有引力定律及牛顿运动定律的人工制造的世界。万有引力定律及运动定律的定义分别如下：

1）万有引力定律：任意两粒子彼此间均是互相吸引的，两个粒子间引力的大小和它们惯性质量的积成正比关系，和它们间欧氏距离的平方成反比关系。但在在GSA中，我们用R代替R2，因为大量实验结果显示，使用R比使用R2的效果更好。

2）运动定律：任意粒子的速度都等于它此时的速度与其加速度之和。加速度都等于作用在此粒子上的外力除以其惯性质量。

2.2 万有引力搜索算法简介

设在一个拥有N个粒子的引力系统中，粒子i的位置是：

其中，xid表示粒子i在第d维空间上的位置。

由牛顿万有引力定律可知，t时刻在第d维上粒子i受到粒子j的作用力为

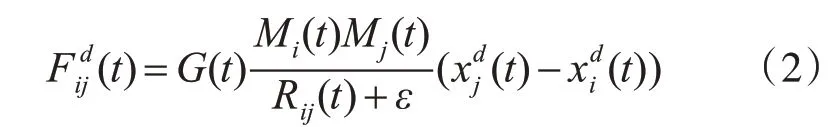
其中，Mi、Mj分别表示粒子i和粒子j的引力质量，ε是一个很小的常量，Rij(t)是粒子i和粒子j在t时刻时它们之间的欧氏距离：

G（t）是t时刻的引力常数，其值由宇宙的真实年龄决定，G（t）的值［8］随着宇宙年龄的增长反而会变小，它们之间的关系如下式所示：

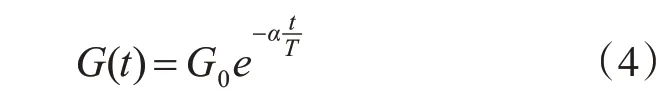
其中，G0代表在宇宙初期的万有引力常数，一般取值为100；α为20；T为最大迭代次数。

为了让GSA有随机性的特点，通常给第d维空间上作用在粒子i上的万有引力的合力设定一个随机数，如下定义：

rand为［0，1］内的随机数。

由运动定律可知，第d维空间上粒子i，t时刻的加速度为

GSA中设定引力质量与惯性质量相等，由适应度函数得出粒子的引力质量的定义：

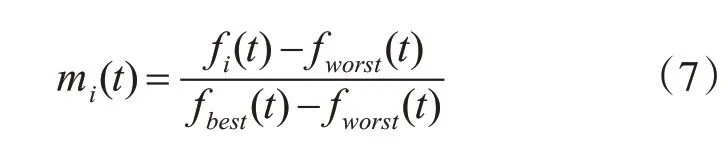
fi(t)为t时刻粒子i的适应度函数值；fworst(t)、fbest(t)分别为t时刻群体最差适应度函数值和群体最好适应度函数值；引力质量一般用单位值表示如下：

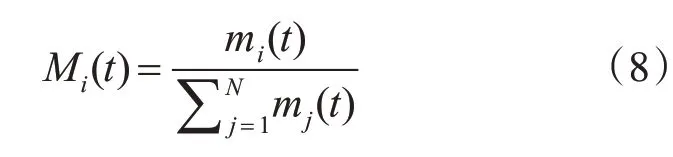
对于求最大值问题：

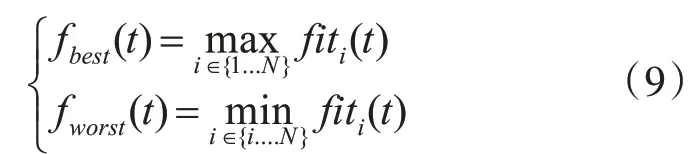
对于求最小值问题：

由以上可知粒子的运动速度和位置分别是：

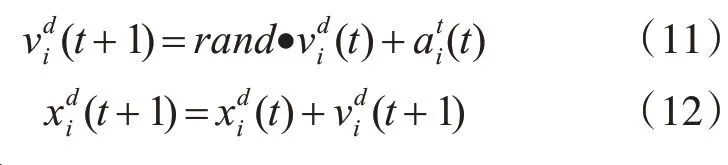
其中，rand是［0，1］上均匀分布的随机数，GSA使用随机数来实现其在搜索过程中的随机性。

3 改进的万有引力搜索算法

对万有引力搜索算法中的速度和位置，由式（11）、（12）分析可知，GSA仅有当前的位置信息在迭代过程中起作用，由此可知万有引力搜索算法是一种缺乏记忆的算法。从式（6）、（11）、（12）可以得知，当粒子运动至最优解或接近最优解之前，由于引力的大小与距离成反比，所以粒子的速度会不断的增加，当粒子运动至或接近最优解时，粒子的运动速度有可能会非常快（存在随机性），由运动学的规律可以知道，上面的情况会致使粒子在最优解周围来回的震荡，从而降低了算法的搜索精度。因此本文将万有引力搜索算法和粒子群算法进行了结合并做以改进。

粒子群优化算法（Particle Swarm Optimization，PSO）是1995年由Kennedy博士和Eberhart教授提出的算法。其它的群体智能算法相类似，PSO也是一种随机搜索的全局优化算法，当对整个群体对解空间中最优解的搜索时，仅需要粒子追随自己及整个群体当前的最好位置移动。

粒子群算法中的粒子的运动速度和位置方程为如下式（13）和式（14）：其中，rand1、rand2为区间［0，1］内的随机数。c1，c2为正常数是学习因子也称为加速系数，c1和c2分别是调整粒子的个体经验和群体经验并对粒子运动轨迹产生影响的重要参数。若c1=0，则仅有群体经验在粒子的运动中起作用，对于复杂问题算法很容易出现局部收敛的问题。若c2=0，则仅有个体经验影响粒子的运动，粒子之间缺乏信息交互的能力。w是惯性权重，w的作用就是为防止算法早熟收敛而产生扰动。pi为粒子i曾经历过的最好位置即个体极值，代表个体经验；gbest为所有粒子曾经历过的最好位置即全局极值，代表群体经验。

借助粒子群优化算法的优点，为引力搜索算法中的粒子增加记忆性和信息共享能力。则将万有引力搜索算法与粒子群优化算法相结合后的粒子运动速度的式（15）：

其中，rand1、rand2和rand3均为区间［0，1］内的随机数；w1和w2均为惯性权重，可以通过调节w1和w2的值来调整粒子在运动的过程中受引力、信息共享的影响程度，显然，当w1和w2为零时改进后的算法退化为引力搜索算法。PSOGSA的流程图如图1。

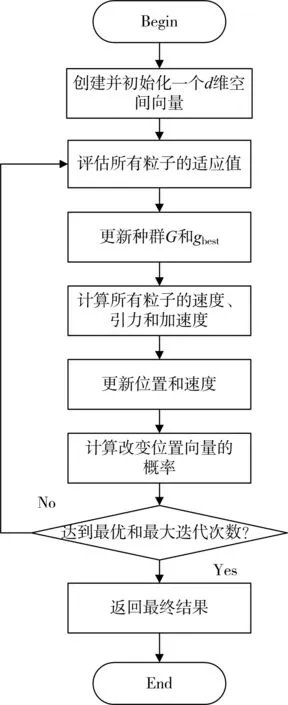
图1 PSOGSA的流程图

PSOGSA能缓解GSA出现的算法停滞的缺点。PSOGSA利用目前所获得的最优解引导惯性质量大的粒子朝全局最优方向移动，而不是所有粒子都朝最优解聚集。显然，PSOGSA也可以加快群体的整体运动，促使PSOGSA算法的寻优能力增强。

图2用y=x2函数显示了GSA在两次迭代过程中粒子的运动情况。M2是一个较优解周围的粒子向M2聚拢。如图3所示，PSOGSA利用目前所获得的最优解引导惯性质量大的粒子朝全局最优方向gbest移动［9］。（M1代表现在搜索所处位置）

图2 GSA在两次迭代过程中粒子的运动情况

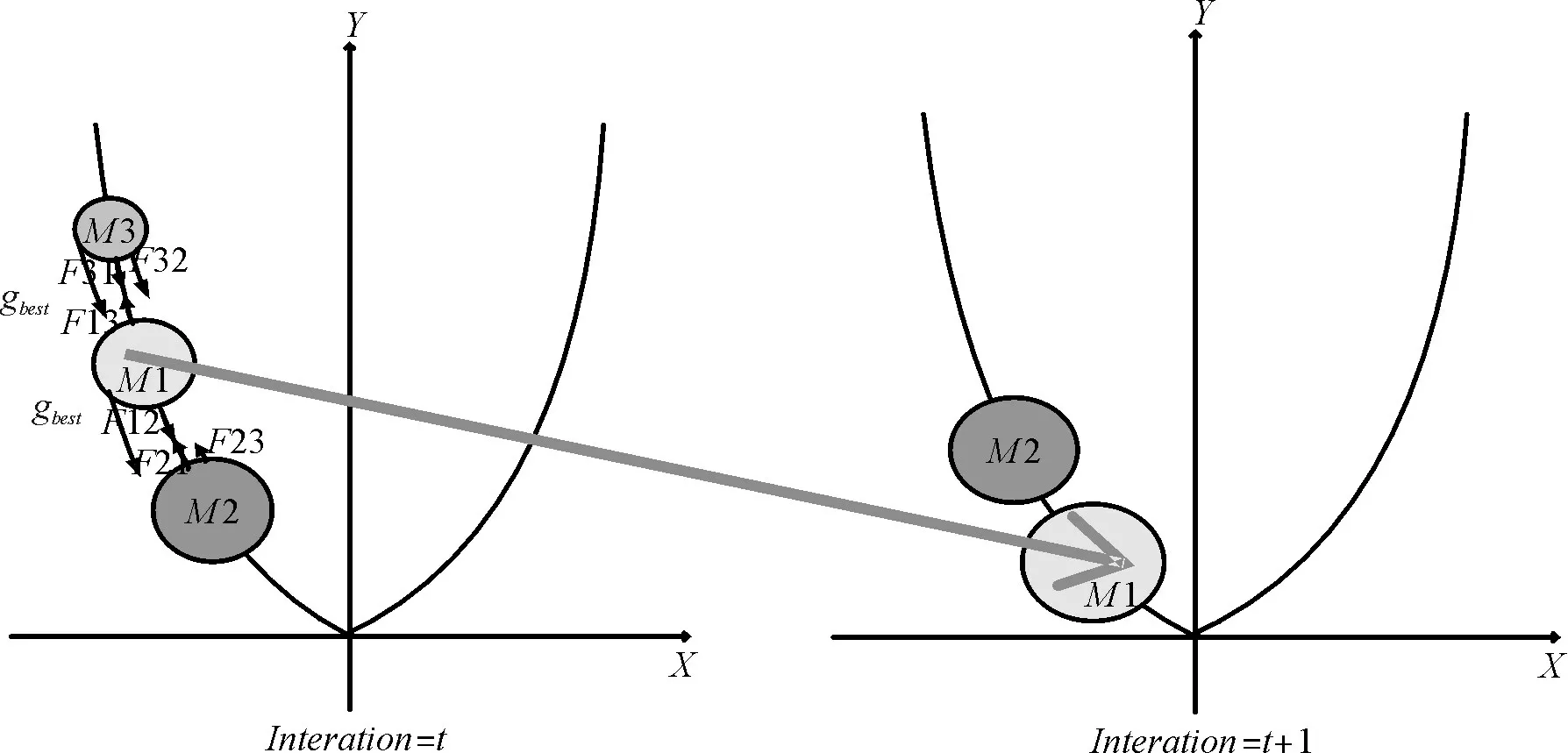
图3 PSOGSA的两次迭代过程中粒子的运动情况

文献［10］通过实验证明，PSOGSA在解决优化问题上要优于PSO和GSA。然而原始PSOGSA主要解决的是连续优化问题，但是实际中有很多优化问题都是离散的比如Web服务选择问题和路由选择问题。为了解决工程实际中众多的组合优化问题，本文借鉴Mirjalili和Lewis提出的二进制PSO算法的理论对原始PSOGSA做以改进。为了让搜索可以在离散的搜索空间内进行，需要修改位置更新式（14）。又由文献［3］和［11］可知，改变搜索代理的位置是需要一个传递函数的，这个传递函数映射速度的值对位置状态改变的概率。文献［12］中例举了许多标准传递函数。根据Mirjalili和Lewis提出的理论可知传递函数应该要保证当速度的绝对值大时，改变位置状态的概率也就大。反之概率小。此外，传递函数是在［0，1］范围内随着速度的增加而增加的。参考文献［3］本文将传递函数定义如下：

图4是对式（16）的说明。

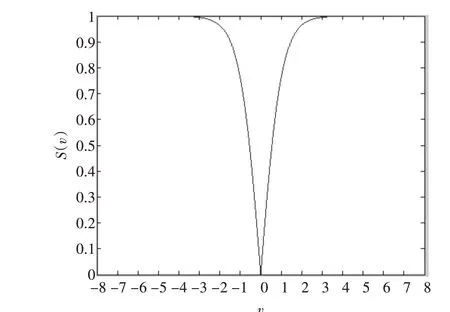
图4 S（v）与v关系

得到S（vid（t））的结果后，搜索代理就会按照下面的规则更新位置：

由文献［13］可知，将gbest加入到速度矢量中会减弱算法的寻优能力，为了解决这个问题，本文对c1和c2做如下变化：

由于PSO算法和GSA算法都存在收敛速度慢，容易出现停滞的现象，也就是说，粒子聚集且运动速度几乎为零，粒子难以逃离局部极值区，从而导致算法早熟。为了避免万有引力搜索算法与粒子群优化算法相结合后的算法出现以上问题，可以通过在进化过程中动态调整搜索空间的边界来进行对粒子飞行位置的追踪，当发现粒子聚集时，通过对边界进行一定的操作和在新的搜索空间内激活停滞粒子，使粒子跳出局部区域，去寻找最优解［14］。

通过如下公式对搜索空间的左边界进行扩展：

上面的式子中，Bdl表示d维下搜索间的左边界，Bdr表示d维下搜索空间的右边界；Cb代表收缩率，-cb=1-cb；Ob代表扩展率。

rand1～rand6是服从［0，1］上均匀分布的随机数。从式（19）～（21）可以看出，通过以全局的极值点为核心在一定范围内进行随机收缩或扩展从而对搜索空间的边界进行调整。若在第d维时当前的边界被重置，则表明在第d维粒子是聚集在一起的，那么，为了增加粒子的多样性在这时算法会随机的挑选少量的粒子进行激活，让其跳出局部极值的区域。

3.1 算法的主要步骤

在每次迭代结束后，算法都会执行下面的3个步骤。

1）标记当前搜索空间的左右边界。在第d维中，查看是否有粒子跳出当前边界［Bdl，Bdr］，若有粒子跳出，则在第d维将边界标识置为true，反之置为false。

2）在此步中，我们将分别处理搜索空间在每一维中的左右边界。如果全局极值点和边界的距离大于阈值ε，且在该维上边界的标识为false，那么使用式（19）对边界进行收缩，否则使用式（20）对边界进行扩展；如果全局极值点和边界的距离小于或等于阈值ε，则表示出现了粒子聚集的现象，那么使用式（21）重置边界。

3）在此步中为了增加粒子的多样性，我们将激活处于停滞状态下的粒子，清除粒子的个体经验。如果在第d维中当前的边界被重置，那么在此时的边界内给速度加上一个服从正态分布的随机数，以便激活粒子。当算法得到最优解或达到最大迭代次数时算法终止。

3.2 服务场景设计与数据组织

采用在Web服务组合领域经常使用的旅游场景，作为验证本文改进的万有引力搜索算法在解决基于多目标优化的Web服务组合问题中的可行性和有效性。在应用场景中，服务请求者只需再提供一些非功能需求如出发日期和酒店等级等信息，作为服务提供者选择最佳方案的依据。服务提供者就会给服务请求者返回一个最优的组合服务。该组合服务按照服务的功能需求需要4个服务类如图5所示：订票、订酒店、租车和找导游服务。为每个服务类选取5个候选服务则共有20个原子服务，从服务日志中读取这20个原子服务的历史QoS信息，经过量纲统一和极性一致性处理，然后基于灰色系统理论对其QoS属性值进行预测，得到各服务类中候选服务的QoS属性预测值如表1～4所示。

图5 旅游场景

表1 订票服务的QoS属性预测值

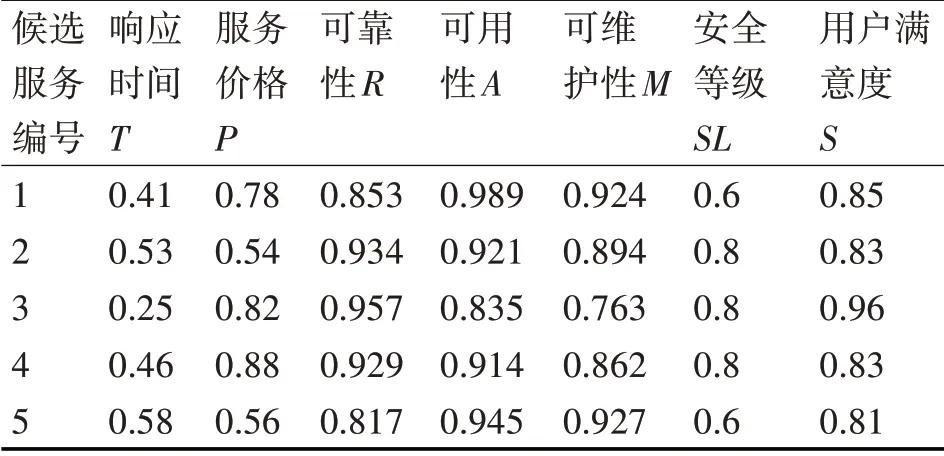
表2 订酒店服务的QoS属性预测值

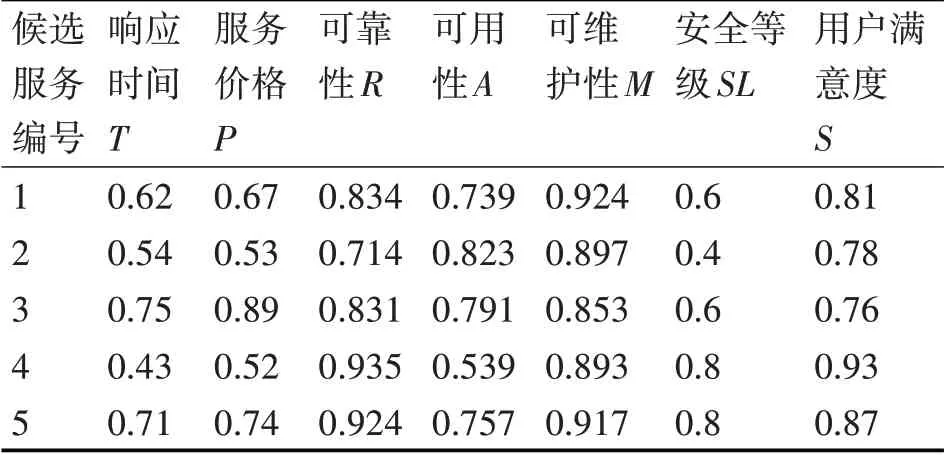
表3 租车服务的QoS属性预测值

表4 找导游服务的QoS属性预测值

根据上述表中给出的预测值，使用穷举法得到的最优服务组合方案的序列是（1，4，5，3），最优值为0.495。得到的最优结果是用于判断后文中用改进万有引力搜索算法得到的结果是否优的依据。

3.3 Web服务选择过程

依据3.2节构造的基于多目标优化问题的Web服务选择模型，应用非功能属性参数也就是QoS属性来评估服务请求中每个服务的适应度函数值。惯性质量按照下面的式（7）更新。fi(t)为t时刻粒子i的适应度函数值，它是由非功能属性参数和t时刻每个服务的适应值来计算的［15］。

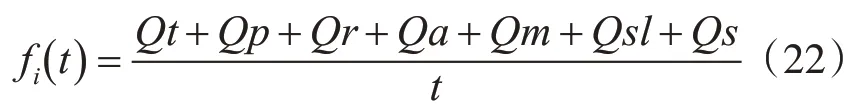
在特殊时刻，

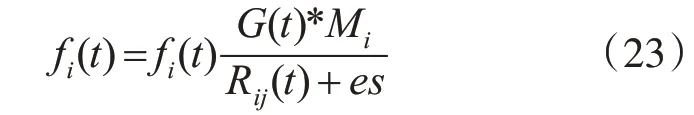
其中，G（t）是t时刻的引力常数，es是一个很小的常数，Rij(t)是t时刻服务i和服务j之间的欧氏距离。

4 实验与分析

为了证明改进的万有引力搜索算法在解决基于多目标优化的Web服务组合问题中的可行性和有效性。使用3.2节中建立的旅游场景和测试数据对改进的万有引力搜索算法进行实验，同时和标准万有引力算法进行对比。实验环境为Windows 7系统，2.27GHz CPU，4G内存，工具为Matlab 7.0，使用语言Matlab。初始参数的设置：种群规模P=80，交叉概率Pc=0.5，变异概率Pm=0.03，最大进化代数T=1000。

表5～7分别代表PSO、GSA和DBPSOGSA算法独立运行十次的结果。

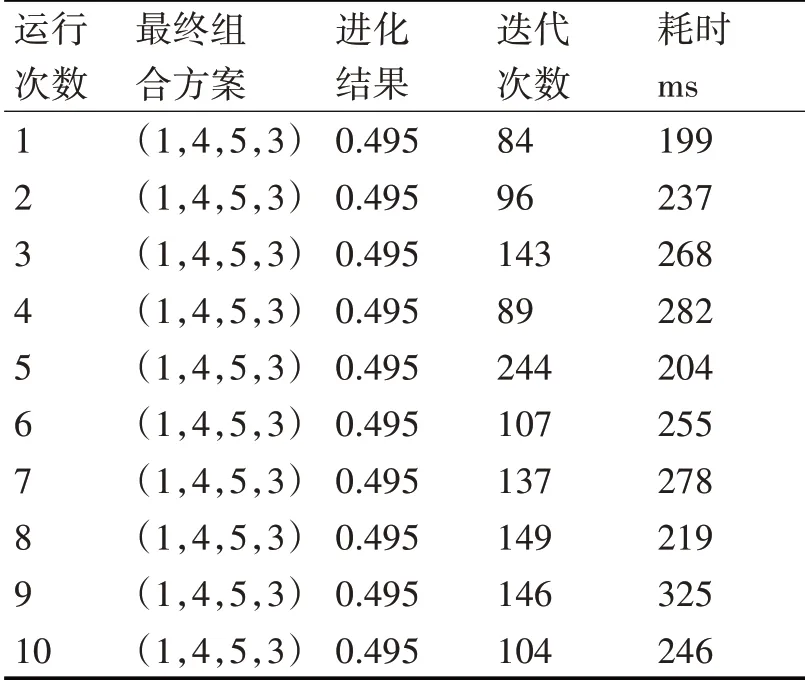
表5 PSO独立运行10次的结果

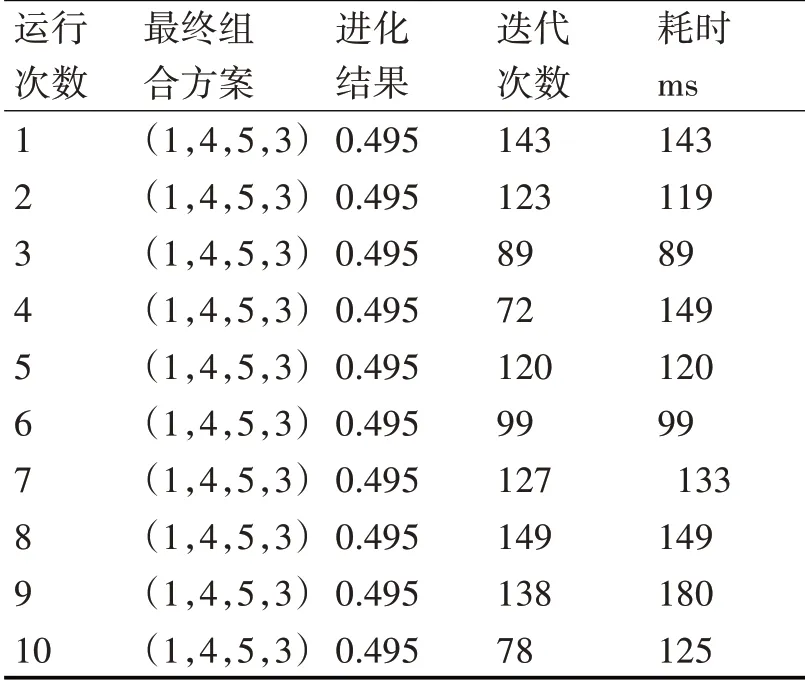
表6 GSA独立运行10次的结果

由表5、表6、表7可知在求解同一规模的问题时，GSA、PSO和本文所提出的DBPSOGSA算法都可以得到最优解，但迭代的次数和耗时是有差异的，图7是这三种算法在求解同规模问题时运行次数和迭代次数对比图。

图6 PSO、GSA和DBPSOGSA求解同规模问题时运行次数和迭代次数对比图

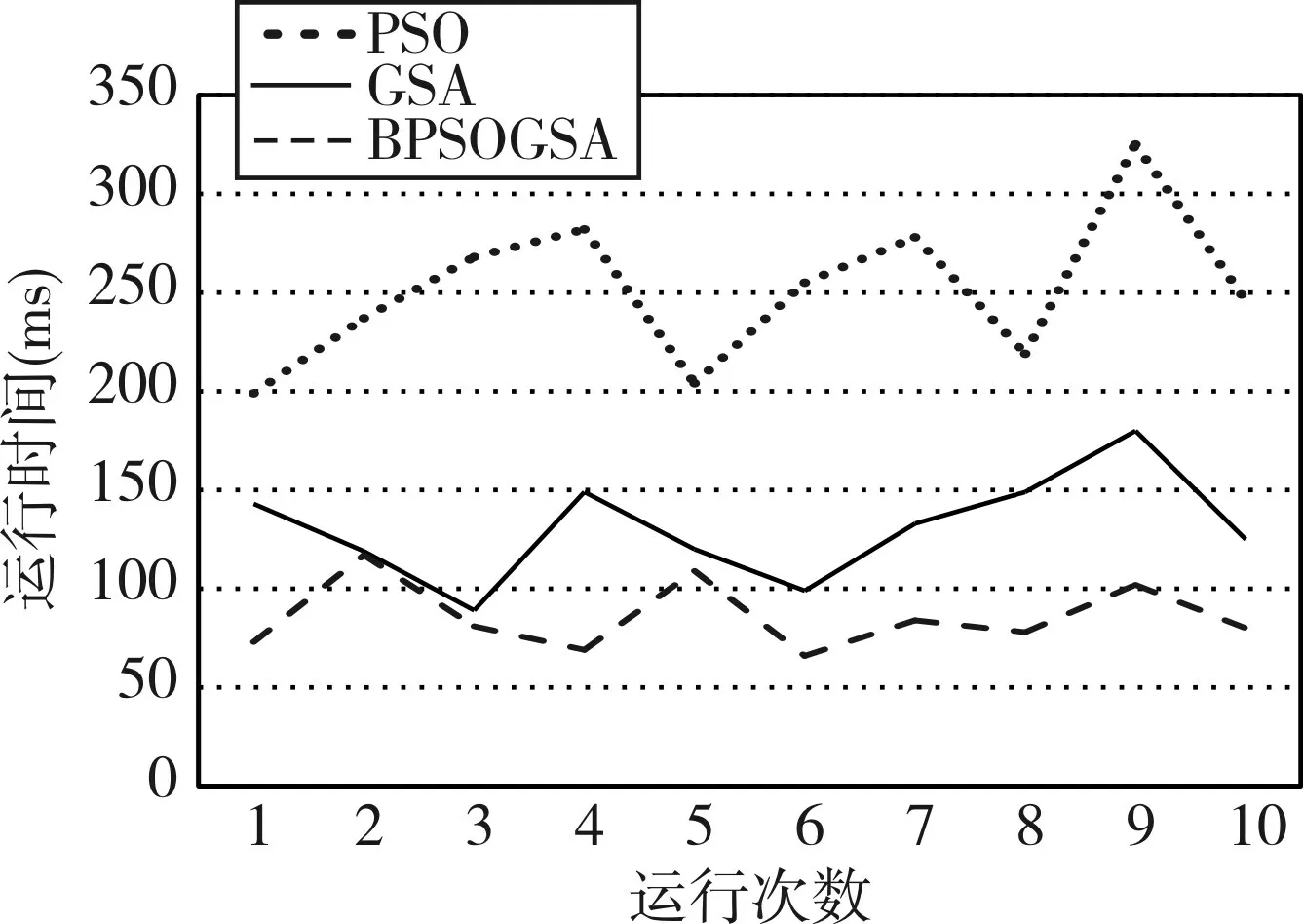
图7 PSO、GSA和DBPSOGSA求解同规模问题时运行次数和运行时间对比图

由实验结果可以看出：PSO算法平均迭代130次左右才可找到最优解，平均耗时251ms，GSA算法平均需要迭代110次可以找到最优解，平均耗时约为130ms，而改进的DBPSOGSA算法平均迭代53次就可以找到最优解，平均耗时约为85ms，该算法在迭代次数和平均耗时上都比PSO和GSA算法有所提升，拥有较好的性能。

引用旅游场景的实验证明改进的万有引力搜索算法在解决基于多目标优化的Web服务组合问题上也具有一定的可行性。

5 结语

本文先是对原始万有引力搜索算法的基本原理和优化过程做以介绍；再通过引入粒子群算法改进GSA中粒子的记忆性，使粒子在优化过程中不但受空间中其他粒子的影响，而且受自身记忆的影响，通过对边界进行一定的操作和在新的搜索空间内激活停滞粒子，使粒子跳出局部区域，去寻找最优解。最后进行了算法和服务性能的对比，证明了所提出的改进的万有引力有较好的性能。

接下来的工作就是进一步验证所提出算法的全局收敛性，以及如何改进万有引力搜索算法使其具有更广泛的适用性。