改进的C4.5算法的研究与应用∗

赵建民 黄 珊 王 梅 刘 澎

（东北石油大学计算机与信息技术学院 大庆 163318）

数据挖掘是对大数据集的探索过程，并揭示出其中的隐含规律，它融合了众多的技术，是计算机科学的一个重要分支。其中分类分析是数据挖掘中重要的分析技术之一，分类分析是根据己有数据样本集的特点发现分类规则，构造分类函数或分类器，从而对未知类别的样本赋予类别，以更好地辅助决策。

目前对涉案人的预警主要运用犯罪专业理论和统计学方法，这些方法大多需要预测人员具备专业的涉案人犯罪经验和领域内的先验知识。同时，对采用较新数据挖掘技术进行涉案人预测挖掘的研究较少［1～3］。数据挖掘中的决策树方法具有可以生成易理解的规则、清晰显示重要字段、计算量较小等优点。应用此方法不要求预测人员具有太多专业领域内的先验知识。

基于决策树的预测方法有很多种类［4］，ID3算法和C4.5算法为最主要的两大算法。其中C4.5算法通过采用信息增益率等方式对ID3算法进行了较好的改进，解决了ID3算法不能处理连续属性和容易选择属性取值较多的值作为分裂标准的弊端，从而使之具有更好的适应性。在应用过程中，由于C4.5算法是按照贪心策略以局部最优的方式构造决策树，此方法下的决策树不一定是全局最优。与此同时，涉案人不同的特征属性的影响程度不同，且不同时间及地点涉案人的特征规律不尽一致，使得运用C4.5算法的分类预测效果并不理想。针对C4.5算法目前存在的问题，相关研究人员提出了使用划分相似度为标准进行C4.5决策树最优特征选取［5］，通过选取多次抽样训练的分类规则进而形成最优规则，在提高该算法准确度的同时还提高了算法的精度，但此方法的使用范围仅限于部分数据集。

本文以C4.5算法的改进作为研究目标，针对涉案人特征挖掘这一问题，提出一种改进的C4.5算法。在C4.5算法中加入加权参数W，即C4.5-W算法。通过对涉案人犯罪数据进行训练得到先验知识-加权参数W，采用C4.5算法对进行预测。

2 改进的C4.5算法概述

将加权参数W与属性选择相结合，降低强关联属性的信息熵，提高某些弱关联属性的信息熵，构造新的决策树模型，提高决策树预测的准确性，为涉案人特征挖掘奠定基础。

2.1 划分信息熵

利用属性V划分样本集S中的数据，计算V对S划分熵值定义为Entropy（S）。属性V分为离散型和连续性两种。

1）V为离散型

取N个不同的值，则属性V依据N的不同值将S划分为N个子集｛S1，S2…，Sm｝。引入参数W后，属性V划分S的信息熵定义为

Si和S中包含的样本个数分别是|Si|和|S|。

2）V为连续型时

利用属性V的取值递增排序，假设S中属性V有N个不同的取值，则排好序的取值序列为a1、a2、…、am，按顺序逐一将两个相邻的值的平均值作为分割点，分割点将S划分为SL和SR两个子集，SL为属性V取值小于平均值的子集，SR为属性V取值大于平均值的子集，对每个可能的分割点计算信息熵为

通过计算并比较属性V所有分割点的信息增益率，选取最大信息增益率作为属性V的信息增益率。

2.2 计算信息增益率

假设划分样本集S为C个类的熵为Entyopy（S），其取值与具体的条件属性无关。则信息增益率计算公示如下：

通过对原有C4.5算法中增益率的计算，推理出新的C4.5算法中信息增益率计算公式如下：

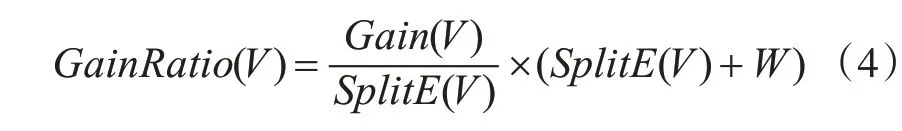
其中，SplitE（V）为按属性V分组的分裂信息，计算方法与C4.5算法相同［6～10］。

2.3 参数W与信息增益率的关系

设样本数据集为Q，包含属性集S。在任意属性V中，设属性V的第i个取值为Vi，则Vi对应的信息熵为Entropy（Si），记为X，即

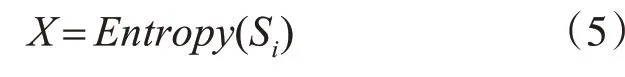
X≥0易在信息熵中得到，且X的取值可以是任意值的非负整数，即x属于［0，+00），按照式（1）和式（2）调整信息熵的取值范围，定义一个带加权参数W的加权信息熵，记为X′，具体定义如下：

其中，k的取值范围为［-1，0］。

设y=GainRatio（V），f（V）=Split（V），y可用如下公式表示：

式（3）中的Entropy（S）取值与属性无关，可取值为常数Z，Z为非负数。定义g（Z）公式如下所示：

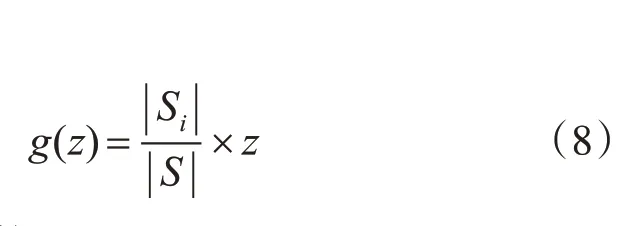
其中，C为任意实数。

经过进一步推理，y的表达式可以进一步如下表示：

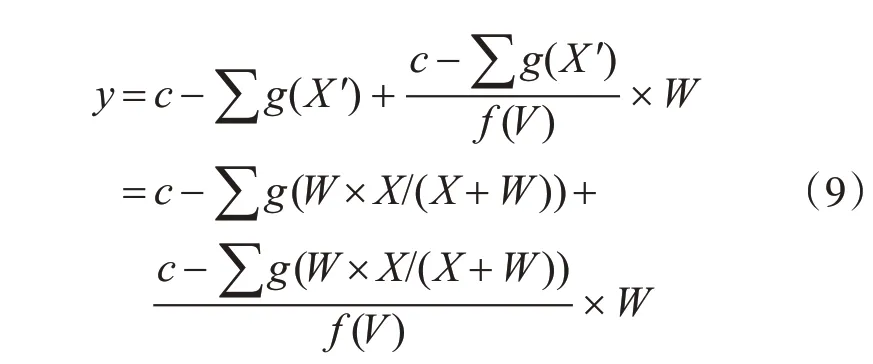
在上述公式的推导过程中可知，C4.5-W算法的信息增益率的取值受x、f（V）、K三个因素的影响。其中，X、f（V）与属性V有关，可通过样本数据计算得出；而W的值与样本的历史数据相关，是一个与具体应用领域有关的先验值或先验知识，需要通过不断训练历史数据进而构建决策树模型得出。

在决策树构建过程中，C4.5-W算法首先需要取初始W值，并判断值的属性为离散型还是连续型，如果为离散型属性，按照式（1）得到信息熵；如果为连续型属性，对数据进行排序后，通过式（2）进行信息熵计算，利用C4.5算法计算信息增益，再采用式（3）计算信息增益率，通过对比不同属性计算的信息增益率值的大小，确定优先分裂的属性。

当生成决策树模型误差率大于指定阈值时，可通过调整W的取值进行反复实验使得决策树模型和样本实际数据接近一致，降低训练误差率，提高预测准确性。

3 实验分析

将涉案人相关数据为例进行训练建模验证C4.5算法的准确性和有效性。涉案人属性主要包括姓名、性别、联系方式、户籍、曾用名、职业、年龄、涉案金额、涉案时间、涉案地点、涉案人是否有过犯罪经历、涉案类别等属性。

3.1 数据预处理

为了方便接下来算法的正常使用，对数据进行预处理，主要方式如下：

1）数据清洗

针对属性下的空缺数据，采用填补该属性下最常见的数值方法，将数据填补完整，针对属性下的噪声数据采用删除的方法［11～13］。由于涉案人中的联系方式、户籍、曾用名等属性对于特征挖掘暂无参考价值，故删除。最后保留下的属性有姓名、涉案金额、涉案时间、涉案地点、涉案人是否有过犯罪经历、涉案类别属性。将此部分属性保留，便于挖掘出各类案件涉案人群在不同时间段下的，不同涉案金额下的，不同年龄段下等的涉案人群特征。

2）数据变换

数据变换是对数据的合并、清理和整合过程［14～17］。以涉案金额为例，将涉案金额换分为各个金额区间，将每个涉案区间用特征数值进行表示，如涉案金额在0～500之间的用数值1进行表示，如果涉案金额区间段划分较多，可在数值1前加入0，即001，将数值位数补全，再将每个区间段用特定的数值表示。

3.2 训练数据及W值的选定

为了选择较适合对历史数据挖掘的W值，以高峰涉案时间段2014年1月1日至2014年3月1日的数据作为训练数据集，经过预处理后的训练数据集如表1所示。

表1 训练数据集

根据2.3节相关理论，在W的取值范围［-1，0］之间，依次取0、-0.1、-0.2、-0.3、-0.4、-0.5、-0.6、-0.7、-0.8、-0.9、-1共11个W值。将W值代入公式（1）～（3），采用Weka API构造出不同W值下的决策树模型，再通过实际中已经侦破案件中的数据分析训练误差。两者比较结果如图1、图2、图3、图4所示。

根据图1～4可以看出K取值为0、-0.1、-0.2、-0.3、-0.4、-0.5、-0.6时，预测数据与实际数据不符的情况较多。

综上所述，W取值在-0.7或-0.8时模型的误差率最低。因此，将W=-0.7对涉案特征进行预测分析对比。

图1 W=0，-0.1，-0.2，-0.3

图2 W=-0.4，-0.5，-0.6

图4 W=-0.9，-1

3.3 实验结果与分析

为了比较C4.5算法和C4.5-W算法的预测能力，以下通过选取2015年12月历史数据生成模型，两种算法得到的模型分别如图5（a）和图5（b）所示。在决策树图中将涉案金额用Money替换，将性别用Sex替换，将年龄用age替换，对比两个图中的属性划分，可以发现改进后的算法通过引入参数W，使得年龄属性重要程度大于性别属性的重要程度。

同样，从图6的预测结果可以看出，C4.5-W算法的预测曲线中预测值与实际值曲线重合度比原始C4.5算法预测曲线重合度高。因此，在C4.5算法中引入参数W可大幅提升算法的准确率。

图5 C4.5算法预测能力

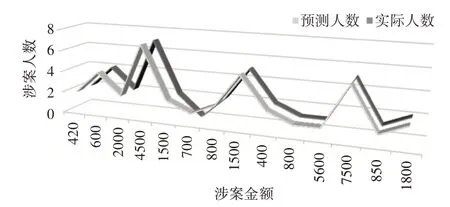
图6 C4.5-W算法预测结果

4 结语

基于涉案人的特征和数据挖掘相关理论，本文通过实验与比较，研究出了一种适合涉案人特征挖掘的决策树算法：C4.5-W算法。通过实验结果表明，C4.5-W算法在预测准确率方面较为精准，能够作为数据挖掘涉案人特征的适用方法。但是也存在一些不足，如没有深入考虑噪声数据等。