多水下机器人编队控制∗

刘瑞轩 张永林

（江苏科技大学电子信息学院 镇江 212003）

多水下机器人［1］的应用广泛。在民用方面有：海底管线铺设［2］、海底考察［3］、水下设备维修等；在军用方面有：海底的排雷、侦察、救生等。AUV的编队队形控制［4～7］越来越受到人们的关注和研究，目前研究使用较多的编队方法有领航跟随法［8～9］、基于行为法［10～11］、虚拟结构法［12］和人工势场法［13～14］。

领航跟随法采用链式的拓扑结构，编队由领航者和跟随者组成，跟随者跟踪领航者来进行移动，从而形成指定的队形；虚拟结构法将队形看成刚体，机器人与刚体上的点进行对应。根据机器人编队运动的环境改变虚拟结构的位置和方向，文献［15］采用AUV曲线路径跟踪算法，AUV在跟踪虚拟结构的过程中形成编队；人工势场法，AUV受到引力向目标移动，AUV受到斥力作用避碰。人工势场法有着陷入局部极小点和死锁的缺点；基于行为法定义了机器人运动的基本行为，对几种定义的行为综合来进行编队整体的队形控制。基于行为法有明确的队形反馈。但是，基本行为法的缺乏理论基础，编队的稳定性没有一定的保证。文献［16］设计了保持队形、奔向目标、切线避碰和随机扰动行为这几种基本行为，通过几种基本行为的优先级来决定机器人的运动，实现了机器人之间的队形保持。

上述几种方法都有各自的不足和需要改进的地方，本文将领航跟随法和基于行为法结合来改善各自方法的不足，用PSO算法对两种方法结合所定义的基本行为组成的适应度函数进行优化，本文算法从机器人传感器探测的环境来进行整体队形的控制。

2 多水下机器人模型以及环境构建

2.1 机器人传感器模型

本文考虑水下机器人的大小和速度并不考虑动力学模型，水下机器人以当前位置为中心rw为半径进行区域内的环境信息探测。在机器人运动的过程中，水下机器人根据自身传感器来探测自身四周的环境来判断当前机器人的运动方向上是否有障碍存在。

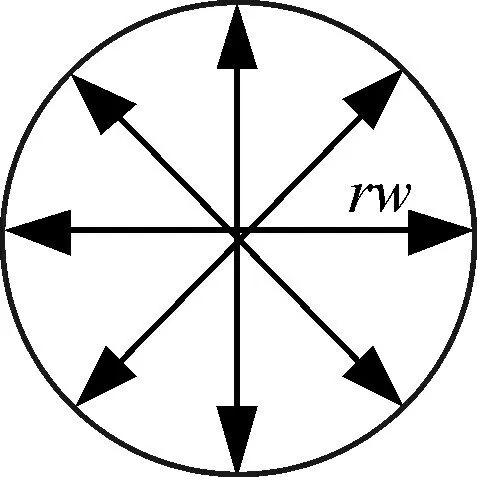
图1 机器人传感器模型

2.2 环境的构建

本文用栅格法来建立机器人运动空间的地图环境，本文机器人的运动为二维运动，在二维空间中建立直角坐标系，整个栅格地图用矩阵M来表示，M（m，n）为1表示在空间（m，n）处没有障碍，当M（m，n）为0表示在空间（m，n）处存在障碍，地图环境中的坐标（x，y）与矩阵M的行列号的关系为

2.3 队形参考点

在编队队形控制中，多水下机器人根据设置的参考点算出自己在队形中的理想位置，让每个机器人之间的相对位置不变从而形成期望的队形或者保持队形不变化。队形参考点的选取有以中心、领导者、相邻参考点三种，本文选择以领导者为队形参考点。

图2 队形参考点选取

3 多机器人队形控制设计

在多机器人编队中，根据基本行为设计目标函数、队形误差函数、避碰函数和避障函数，通过对上述函数加权平均构成适应度函数。然后采用PSO算法对适应度函数优化来对多水下机器人控制。

3.1 奔向目标函数

机器人Ri的驶向的目标点为(Gix,Giy)，第K步机器人Ri的所处位置为(xi(k),yi(k))，机器人Ri在第K步驶向的目标函数为

3.2 队形误差函数

在传统的领导者-跟随法中，领导者向目标点移动，跟随者跟随领导者移动并保持队形不变。传统的方法对领导者太过依赖，领导者运动速度过快或过慢会导致跟随者跟不上领导者，从而没有良好的队形反馈使得编队不能保持队形。为解决该问题，本文设计了队形误差函数。

1）菱形队形误差公式

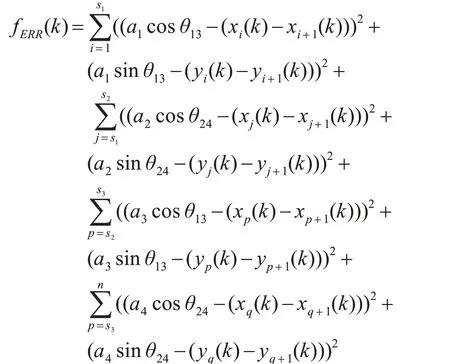
a1=l/(s1-1) a2=l2/(s2-s1)a3=l/(s3-s2)a4=l/(n-s3+1)，l为菱形边长，ai为菱形第i条边上两个机器人的距离，θ13为菱形的第一条边和第三条边与X轴正方向之间的夹角，si是i条边机器人的编号，机器人的数量为n。

2）直线队形误差公式

a=l/(n-1)，l为线性长度。

3.3 避碰函数

在编队控制中，水下机器人Ri进行运动前，Ri把自己传感器所探测到的环境信息广播给其他机器人。其他机器人Rj收到广播信息后再来决定自身的运动。当Ri与Rj之间的距离小于安全距离d时使用避碰函数进行避碰，避碰函数定义为

3.4 避障函数

当水下机器人传感器检测在行进中有障碍物阻碍其前进时，我们使用避障函数来避障。定义的避障函数为

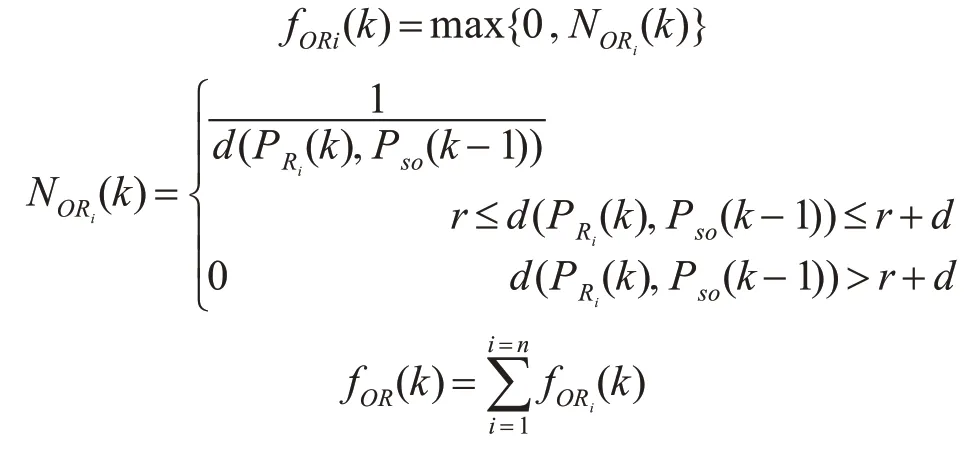
PRi(k)为Ri在第k步的预期位置，PSO(k-1)为第k-1步检测到障碍物的边沿位置，n为机器人个数，d为障碍物危险区域范围。

3.5 粒子群算法

在N维空间，群体由N个粒子构成，粒子i的位置与飞行速度为Xi(Xi1,Xi2,Xi3…Xin)和Vi(Vi1,Vi2,Vi3…Vin)，在每次迭代中粒子跟踪极值来改变自身的位置和速度。个体极值Pi(Pi1,Pi2,Pi3…Pin)，即粒子经历过的最好位置；全局极值Pgi(Pg1,Pg2,Pg3…Pgn)即全部粒子经历过的最好位置。粒子i的速度以及位置由下面的公式来更新：

Vij(t),Xij(t)分别为第t代种群中第i个粒子第j维的速度和位置；Pji(t)为粒子的最优位置；Pgi(t)为种群的全局极值；c1为认知系数，c2为社会认知系数；r1和r2分别为独立的随机数；w为惯性权重。

在队形控制任务中，跟随机器人以领导者为整个队伍的参考点。粒子群算法对基本行为法构造的奔向目标函数、队形误差函数、避障函数和避碰函数组成的适应函数进行优化，适应度函数如下：

f(k)=w1fmtg(k)+w2fERR(k)+w3fRR(k)+w4fOR(k)

水下机器人在向目标的前进时首要是进行避碰和避障，然后才是保持队形。w1、w2的选择根据探测的环境进行调整，权值的大小代表对目标的偏好程度。为了防止机器人与障碍和自身除外的其他机器人发生碰撞，w3、w4值为1。当保持队形为首要任务时w1=2、w2=1；当避开障碍物为首要任务时w1=1、w2=2；当两者同样重要需要保持平衡时w1=1、w2=1。编队控制的算法流程图如图3所示。

图3 编队控制算法

4 多水下机器人队形控制仿真

本仿真选用Matlab平台进行仿真，编队队形控制以领导者为队形参考点，四点移动到预期位置形成菱形，起始点为坐标为（11，25）（8，34）（7，26）（9，16），形成预期菱形位置为（18，13）（20，15）（20，11）（22，13），灰色表示目的地点坐标为（36，29），栅格环境中的黑色障碍物是未知的，水下机器人依靠传感器进行障碍物探测通过算法进行每一步移动，（a）～（c）为队形形成过程，（d）～（e）为队形保持过程，（f）～（h）为队形变换。

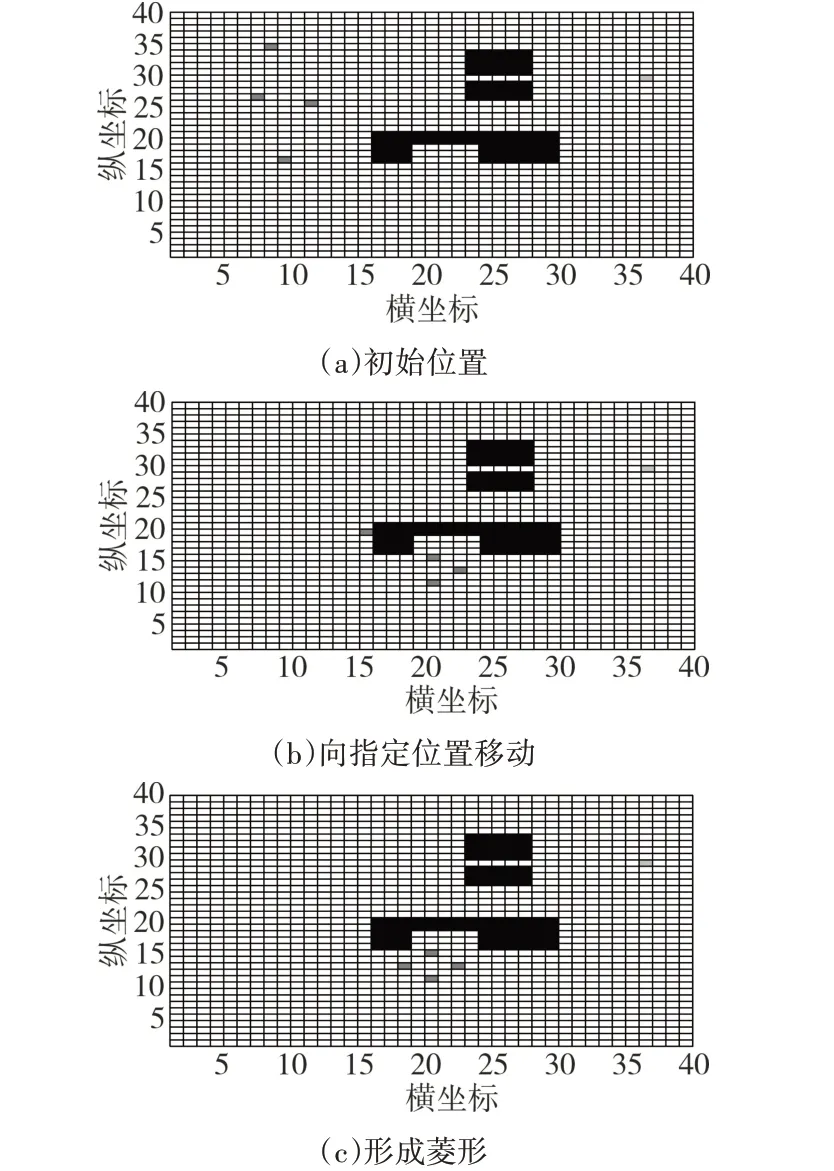
图4 队形控制仿真

5 结语

本文将领航跟随者法和基于行为法两种方法结合，粒子群算法对多水下机器人队形控制的基本子行为奔向目标、保持队形、避碰、避障的函数所组成的适应度函数进行优化。从队形形成、队形保持、队形变换的仿真结果来看，多机器人可以从随机初始位置无碰的到达了指定位置形成队形。在形成菱形后奔向目标点的过程中，在编队行进过程中队形良好的保持了菱形。当机器人碰到狭窄通道时，这时候菱形队形将队形变换成直线队形后通过狭窄通道，直线队形通过狭窄通道后又恢复成原来的菱形队形向目标点前进，最终到达所设目标点。从上述仿真实验来看，多水下机器人的编队控制算法具有很好的稳定性和适应性。