一道诊断考试题的推广探究
2019-02-26 01:02董强
数理化解题研究 2019年4期
董 强
(甘肃省西和县第一中学 742100)
2017年甘肃省第一次诊断考试中的圆锥曲线试题是探究是否存在两个定点,使得给定表达式为定值的探究问题,有别于以往的是否存在一个定点问题的探究,其中所涉探究过程均依托于圆锥曲线的定义.笔者觉得颇有研究的价值,也是一种新的命题方向,在此将试题解析与推广探究过程与读者分享,以引起更多师生的关注.
一、试题呈现

(1)求椭圆C的方程;

二、试题解析

解析设P(x0,y0),M(x1,y1),N(x2,y2).

即x1x2+2y1y2=0(*).




三、推广探究
对上述试题第二问的结论可以作以下一般性的推广:



圆可以看作椭圆的特殊情形,于是在圆中有如下的结论.
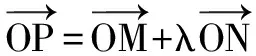
双曲线和椭圆具有很多相似的性质,上述结论还可以在双曲线中做一般性的推广.

证明设P(x0,y0),M(x1,y1),N(x2,y2).

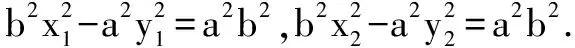
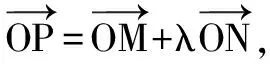




对于焦点在y轴上的椭圆和双曲线,上述相应的结论依然成立.
结论1和结论3虽然隶属不同的曲线类型,但其形式上是相同的,可以将二者合并为如下的结论.


猜你喜欢
中学生数理化(高中版.高考数学)(2022年4期)2022-05-25
中学生数理化(高中版.高考理化)(2022年2期)2022-04-26
今日农业(2021年21期)2021-11-26
新世纪智能(教师)(2021年2期)2021-11-05
中学生数理化(高中版.高考理化)(2021年5期)2021-07-16
教育周报·教育论坛(2021年21期)2021-04-14
中等数学(2020年4期)2020-08-24
中学数学杂志(2019年1期)2019-04-03
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16
中学数学杂志(2015年9期)2015-01-01

