点线面位置关系学习的主导思想方法研究——以《空间点、直线、平面之间的位置关系》一节为例

陈小娟

(福建省漳州市华安县华安一中 363800)

某种学习内容主导思想方法的寻得是在全面掌握此种内容，并能剖析出清晰的筋骨脉络的基础上进行的，这便需要教师在其PCK，即学科教学知识的支撑下，将知识浓缩成精华，升华为思想方法引导学生习得知识、提升思维与数学素养，这也便是在点线面位置关系这一学习内容本身之外要对其思想方法进行研究的缘由.所以，针对这一内容，我总结出三种有效的思想方法：思维伸缩法、梳理法、平面立体转化法.

一、思维伸缩法——平面与直线的延伸和限制

在高中低年级学段，学生关于教材权威性的认知依然没有得到突破性的改变，其学习过程遵循的依旧是意识毫无选择与反思地全面接受教材的模式，这确乎为学生获取系统知识提供了保障，但也造成了其对错误知识的无条件接收，除此之外更为严重的是其思维局限惯性的逐渐形成与渐渐远离数学学习锻炼思维能力的初衷的后果.所以，教师要适时地在教学过程中补充呈现教材中没有体现或体现不明显但却对学生对于知识的整体理解容易造成误解的相关知识，避免学生学习误区，慢慢养成真正的数学学习所需要的开阔灵活的思维方式.

例如：在引入点、直线、平面这三个图形构成基本要素的环节，书本上呈现的大多是尺寸有限的直线和平面，但在实际的空间几何中，它们是无限延展的.这一概念虽然对学生理解和运用课本知识并无大碍，因为涉及到的原理与题目几乎皆基于直线和平面有限的呈现，但如若学生意识中缺失了这一概念，那么这种缺失使其对于立体几何的本质认识造成的误解却是根源性的.所以，在点线面的概念引入之初我便向同学们明确强调了这一点，同时阐明这种为了研究方便而化无限为有限的数学方法，在保证学生接收线面知识正确性的同时，有效拓宽了其数学思维，教会学生灵活处理问题的建模方法.

二、梳理法——相交与平行的二重可能性

任何一个方面的知识都会随着研究深度的增加而逐渐细化、复杂化，所以，对其进行掌握需要的便不再是费时费力的对于每个知识点的分散记忆，而是打通知识间的经脉，发现知识的相似性与独特性，进而进行梳理.这样的方法，不仅能够使知识有逻辑地呈现，方便自己管理和记忆，由此，也会更深刻全面地认识到数学事物、规律的本质.这里的直线与直线、直线与平面、平面与平面之间的位置关系，三者皆具有某一共性，即非相交、即(不相交)平行的二重可能性，所以，教师要在教学过程中利用这种非此即彼的概念，锻炼学生的空间想象能力和全面思考问题的能力.

例如：在探究直线与平面之间的位置关系时，我带领同学们多次对两者可能的状态进行演示实验，之后，总结出三种可能性：直线在平面内、直线与平面相交、直线与平面平行.

在之后的对平面与平面位置关系的研究中，进行同样的操作实验，发现了两种位置状态：平面与平面平行、平面与平面相交.由此，同学们会发现位置关系平行、相交的二重可能性.多次实地的演示与探究大大锻炼了同学们的空间想象能力和依托空间想象进行对空间事物状态判断的能力，而且抓住了平行、相交这一位置关系研究的中心点，依此实现对点线面位置关系更深入和牢固的把握.

三、平面立体转化法——平面立体位置关系

多维立体空间和单维平面其实是两个相互依附、可以相互转化的存在：单维平面构成立体几何，多维立体拆解成单维平面.所以，有时我们可以将空间问题有意识地转化为平面问题以达到方便研究的目的.但由于这种转化涉及到空间中的动态平移，所以它需要强大的空间想象能力，这对高一新生来讲，确乎有一定难度，但是引导学生在脑海中实现这种转化的过程同样也恰恰是锻炼其空间想象能力的过程，即双赢共进.所以，教师要充分运用这一原理，在相关内容模块积极引导学生进行由立体到平面的想象转化，加深对立体几何点线面位置关系的理解和掌握.

例如：在直线与直线之间的位置关系中存在一种既非平行，也非相交的情况，即不同在任何一个平面内的异面直线，类似以下图形中AB线段和CC′线段所在的直线：

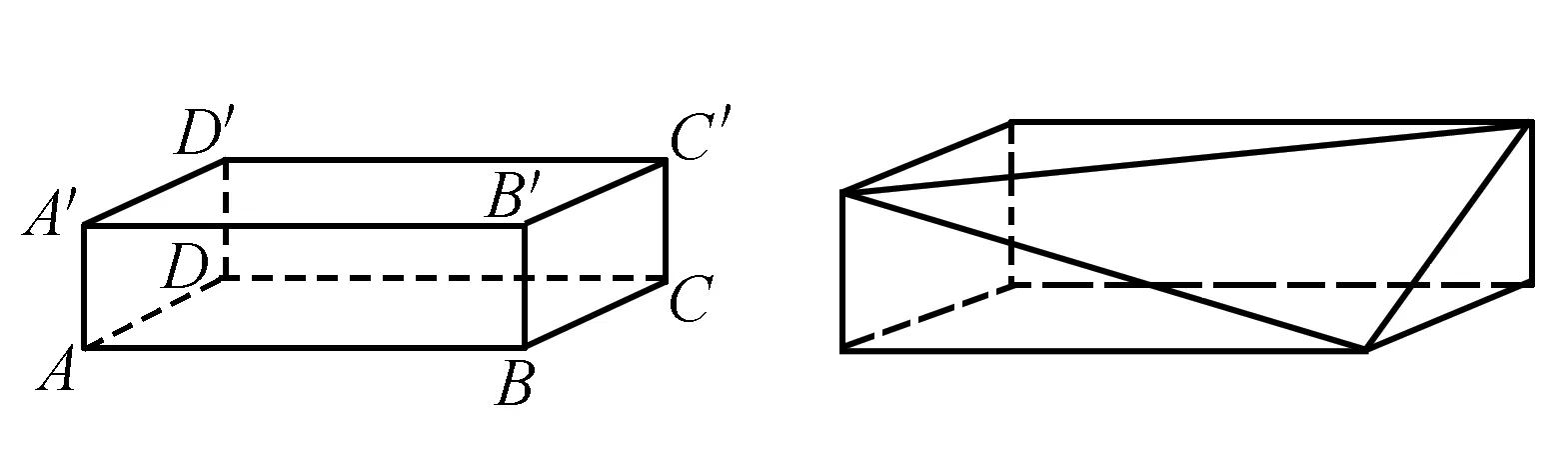
图1 图2

那么，如何利用常见的用两条直线的夹角来度量异面直线的位置关系呢？即如何求两条异面直线所成的角？解决这一问题便需要将CC′所在直线平移至BB′所在直线，或将AB所在直线平移至CD所在直线，使得两条直线在同一平面内，如此便能轻松得到两条异面直线所成的角.除此之外，它还涉及之前学习内容的立体几何体三视图与之后的关于立体几何的更深一步学习，如需要剪裁拼接某立体图形的某一部分以方便剖析研究等，如图2.一个长方体截去一个三棱锥所得的横截面与以此形成的长方体各个平面的变化，都涉及动态平移、平面和立体之间的转化等.可见，这种转化几乎贯彻立体几何内容的方方面面，所以这一点便当之无愧成为这一节内容的一大主导思想之一.

立体几何是高中数学学科中极为重要的内容，也是高中生数学理性思维培养工程的一大环节，所以，对于其具有基础性的点、线、面的位置关系便成为教师教学与学生学习需加重视的一项内容.而且其中涉及到的直线平面的无限延伸性、相交平行的位置关系二重可能性与单维平面和多维立体之间的转化关乎整个立体几何的学习过程.由此可见，这一节内容的关键性与上文中述说的三个主导思想方法的重要性.