也谈对2017年全国卷Ⅲ第12题的赏析与拓展
2019-02-26 00:50董安林
数理化解题研究 2019年4期
董安林
(甘肃省金昌市第一中学 737100)
文【1】从坐标法、基向量法、数形结合法三个视角,使用四种方法对2017年全国卷Ⅲ第12题进行了解析.笔者对此题的解析也略有心得,特撰此文,与各位同仁共赏.


于是,有如下结论成立:
(1)当P∈直线AB时,λ+μ=1;


证明(1)当P∈直线AB时,A,B,P三点共线,由三点共线性质可知λ+μ=1,结论(1)得证.
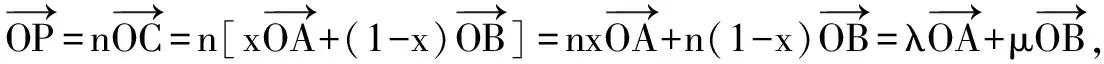
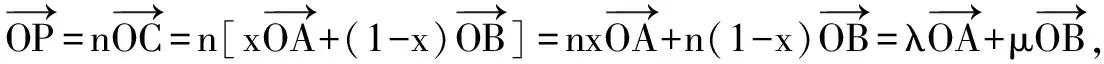
①当P∈Ⅱ区且在AB与l之间时,如图2所示.
②当P∈Ⅱ区且与AB在l的异侧时,如图3所示.
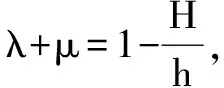

下面应用以上定理逐一解决文【1】中的所有问题.
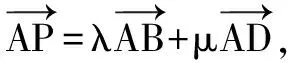


变式1 求λ+μ的最小值.
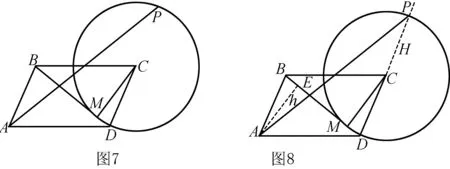
解析如图5,当点P与M重合时,P距离直线BD最近,此时P∈BD,λ+μ=1,问题得解.
变式2 求λ+2μ的最大值.

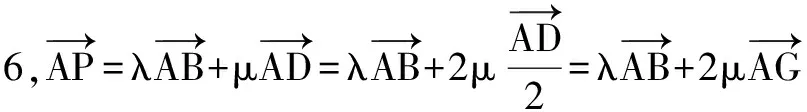
过A作AE⊥BG=E,记AE=h,过C作CF⊥BG=F且交圆C于点P(较远的交点),此时P距BG最远,λ+2μ取得最大值.

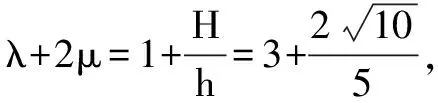
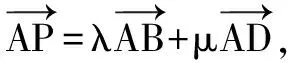

猜你喜欢
新高考·高一数学(2022年3期)2022-04-28
中等数学(2021年4期)2021-08-14
中学生数理化·高一版(2021年5期)2021-07-21
石家庄铁路职业技术学院学报(2021年1期)2021-06-09
快乐学习报·教师周刊(2021年37期)2021-02-07
中学生数理化·七年级数学人教版(2020年12期)2021-01-18
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
祖国(2018年3期)2018-03-26
中学生数理化·七年级数学人教版(2017年3期)2018-01-20
课程教育研究·学法教法研究(2016年27期)2017-04-21

