更换主元 巧解一道高考压轴题
2019-02-26 01:01:10任孝辉时英雄
数理化解题研究 2019年4期
任孝辉 时英雄
(安徽省合肥市第一中学 230601)
原题再现:(2016年高考新课标Ⅲ卷文)设函数f(x)=lnx-x+1.
(1)讨论f(x)的单调性;

(3)设c>1,证明当x∈(0,1)时,1+(c-1)x>cx.
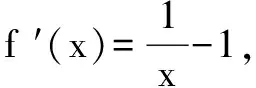
当0
(2)由(1)知,f(x)在x=1处取得最大值,最大值为f(1)=0,
所以当x≠1时,lnx (3)由题设c>1,设g(x)=1+(c-1)x-cx,则g′(x)=c-1-cxlnc. 当x 所以当x∈(0,1)时,1+(c-1)x>cx. 试题新解(1)(2)略. (3)由题设x∈(0,1),c>1,设h(c)=1+cx-x-cx=xc-cx+1-x,c>1. h′(c)=x-xcx-1=x(1-cx-1).∵x∈(0,1),∴x-1∈(-1,0). ∴函数m(c)=cx-1在(1,+∞)上是单调递减函数, ∴cx-1<1x-1=1,∴1-cx-1>0. ∴h′(c)=x(1-cx-1)>0,h(c)在(1,+∞)上单调递增. ∴h(c)>h(1)=x-1+1-x=0,所以当c>1,x∈(0,1)时,1+(c-1)x>cx,得证. 评注试题原解构造关于x的函数g(x)=1+(c-1)x-cx,通过对其求导利用(2)的结论,判断出极大值点x0∈(0,1),得证.新解中构造关于c的函数h(c)=xc-cx+1-x,更换了主元,通过求导直接判断出导函数大于零,证出单调性,使得问题简化许多,进而得证.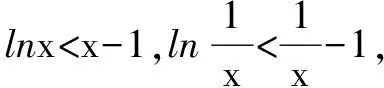
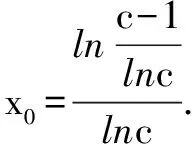
猜你喜欢
数理化解题研究(2022年22期)2022-08-30 06:37:58
中学生数理化(高中版.高二数学)(2022年6期)2022-06-30 06:36:02
中学生数理化(高中版.高二数学)(2022年6期)2022-06-30 06:36:02
中学生数理化(高中版.高二数学)(2021年4期)2021-07-20 07:18:48
河北理科教学研究(2021年1期)2021-06-07 07:49:14
高中数学教与学(2020年21期)2020-11-27 06:41:28
初中生学习指导·提升版(2020年11期)2020-09-10 07:22:44
中学数学杂志(初中版)(2019年4期)2019-09-18 15:15:11
新高考·高二数学(2018年1期)2018-11-20 02:15:42
文理导航(2018年2期)2018-01-22 19:23:54

