基于比例边界有限元广义形函数方法模拟混凝土裂纹扩展问题

章 鹏，杜成斌，张德恒

（1.南京工程学院，江苏 南京 211167；2.河海大学 工程力学系，江苏 南京 211100）

1 研究背景

在准脆性材料（如混凝土、岩石）的断裂问题中，当裂纹面的法向张开位移以及切向滑动位移较小时，裂纹面之间由于骨料互锁以及表面摩擦，还具有相互作用，存在着一定的黏聚力，构成了断裂过程区（Fracture Process Zone，FPZ）。许多学者提出了考虑断裂过程区的混凝土非线性模型，其中Hillerborg 等[1]提出的虚拟裂纹模型，由于能够准确模拟混凝土材料的能量扩散过程，在混凝土非线性断裂模拟中得到了广泛的应用和研究。

有限元法（Finite Element Method，FEM）是分析材料非线性以及非连续问题的主要方法，在有限元法中，通常采用零厚度界面单元[2]对混凝土结构的开裂进行模拟，然而在有限元中，由于需要在裂纹尖端布置很密的网格[3]或者采用特殊单元[4]（奇异单元）模拟裂纹尖端应力奇异性，此外在裂纹扩展过程中需要进行网格重划分，十分繁琐甚至无能为力。为了解决有限元在处理裂纹扩展时重划分网格较为困难这一问题，文献[5]提出了引入节点富余项的扩展有限元法（Extended Finite Element Method，XFEM），该方法被广泛地应用于模拟混凝土非线性断裂问题中，但在描述裂纹尖端的应力应变时仍需要很密的网格。Wells等[6]采用六节点三角形单元，在扩展有限元法框架内引入黏聚力模型模拟三点弯梁的裂缝扩展。Zamani等[7]采用含黏聚力的裂缝尖端渐进解的高阶项作为XFEM裂缝尖端的富集函数，模拟非线性裂缝扩展。

比例边界有限元法（Scaled Boundary Finite Element Method，SBFEM）是计算混凝土非线性断裂力学的一种新型的具有半解析解的数值计算方法，该方法由Wolf和Song在1990年代末率先提出[8-9]。SBFEM方法在计算过程中仅需离散结构的边界，降低了一维数值模拟维度，而且可以半解析地表征裂纹尖端的奇异性[10-11]。基于上述不可替代的优点，SBFEM在工程问题方面的应用正逐渐成为学术研究的前沿和热点[11-13]。在模拟混凝土非线性断裂问题中，Yang等[14]率先提出了一种简单的适用于SBFEM的网格重划分方法，并首次采用该方法来模拟混凝土黏聚裂纹的扩展，但是该方法在处理复杂结构时会出现失效的情况。随后，Ooi 等[15]采用多边形SBFEM 单元对混凝土黏聚裂纹的扩展进行了模拟，在裂纹扩展过程中，可局部自动划分网格，提高了计算效率，模拟混凝土断裂过程区能量耗散的黏聚力时皆采用在网格中插入耦合界面单元方法。朱朝磊[16]通过引入线性渐进叠加假设对该方法进行了改进，在裂尖单元采用特解方法将裂尖单元的黏聚力（侧面荷载）施加在裂纹面上，模拟得到了与试验及其它数值方法较为一致的结果。

本文在比例边界有限元基础上，对比例边界有限元广义形函数方法进行研究，考虑侧面荷载的影响，在单元的位移插值函数中附加内部无结点的位移项，该项的物理意义反映侧面荷载对单元内位移的影响。其形函数具有与非协调有限元形函数相一致的形式，但该方法相较于非协调有限元具有自然满足单元交界面连续性的优点。然后采用该方法对混凝土非线性裂纹扩展进行模拟，其中在裂纹扩展步中采用线性渐进叠加假设，在断裂过程区，裂尖单元以及非裂尖单元中的黏聚力采用形函数以等效荷载的形式统一施加在单元节点上。最后通过两个典型算例验证采用SBFEM形函数方法模拟混凝土黏聚裂纹扩展的准确性和有效性。

2 含有侧面荷载的比例边界多边形有限元广义形函数

如图1（a）为一个普通SBFEM多边形单元，在该单元内，需要选取一个比例中心，该比例中心需要满足在该处可以看到单元的全部边界。图1（b）为具有裂纹面任意荷载的比例边界有限元单元模型，其中O（裂尖）为比例中心，断裂问题比例中心通常选在裂尖处。定义ξ(0 ≤ξ≤1)为径向坐标，s(0 ≤s≤1)为环向坐标，模型边界(ξ=1) 离散成一维线单元，而裂纹侧面不需要离散。ξ-s形成比例边界有限元局部坐标系，环向坐标s正向沿着单元边界逆时针变化，径向坐标ξ正向沿着比例中心向外变化，其中ξ=0 代表比例中心O，ξ=1代表边界上的点。

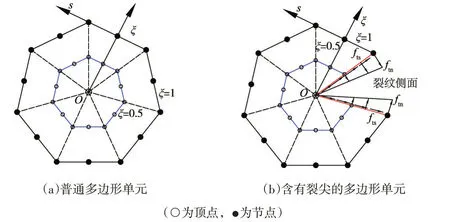
图1 多边形SBFEM单元

对于裂纹单元内任意一点，相对于比例中心的坐标(x，y)可用ξ和s表示为：

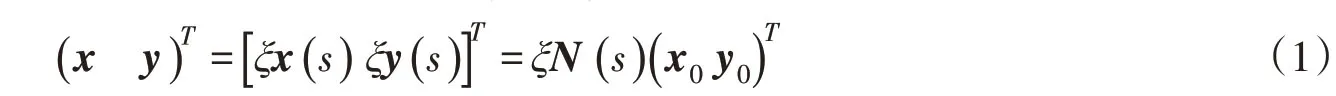
式中：(x0y0)为边界上的节点坐标；为沿s方向的形函数。

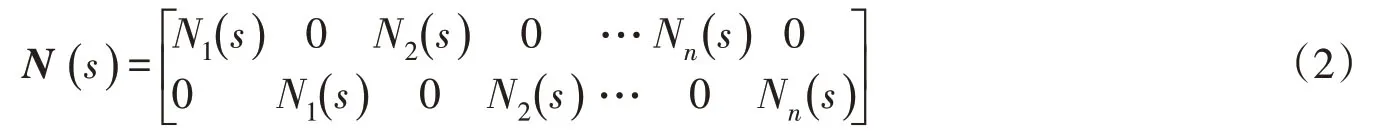
其中n为边界节点个数。

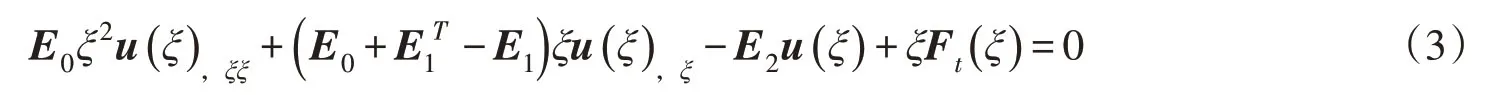
考虑侧面荷载的比例边界有限元的控制方程可通过加权平均法[8]或者虚功原理[9]得到径向上的平衡方程：式中：E0、E1、E2为单元的系数矩阵，详细表达式可见文献[9]；Ft(ξ)为侧面荷载；u(ξ)为节点位移函数。

裂纹上的侧面荷载Ft(ξ)

ξ可以分解为关于ξ的M阶多项式函数：

式中：Wi为单元侧边力分布矩阵；ai为第i阶侧面荷载多项式系数。

式（3）为关于ξ的二阶非齐次方程，可以由通解加上特解的解析形式求解[14]，解的形式为：

式中：ψd为单元的模态位移矩阵；Λλ为对应的单元特征值矩阵；c为单元积分常数组成的列向量，可由边界条件确定；Vt为侧面荷载的模态位移矩阵；Λt为对角矩阵，Λt=dig(1，2，3，…，M)；a为组成的列向量，

积分常数c用边界位移表达为：

其中ub为边界节点位移。

将式（6）代入式（5）可得：

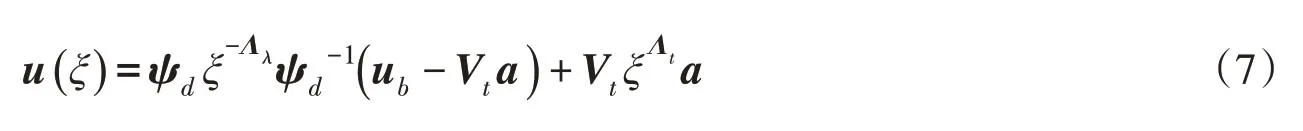
式（7）采用矩阵形式可写为：

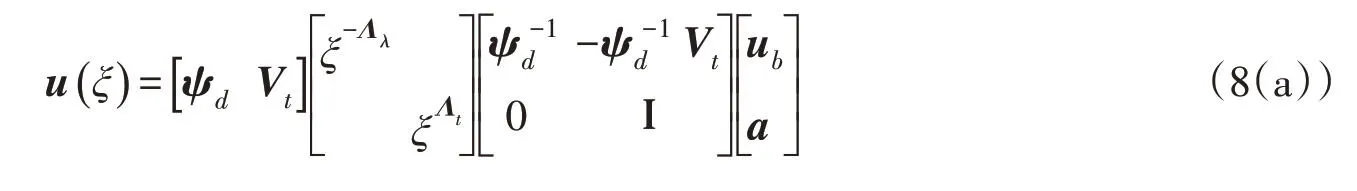
令

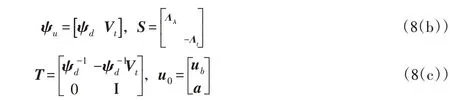
将式（8（b））、式（8（c））代入，则式（8（a））可改写为：

比例边界有限元在环向s上采用与有限单元法中形函数类似方法，通过N(s) 进行插值，即：

将式（9）代入式（10）可得：

令：

可得：

由式（13）可知，N(ξ，s)为采用比例边界有限元法考虑侧边力任意荷载时的形函数。将式（8（b））和（8（c））代入式（12），得到：

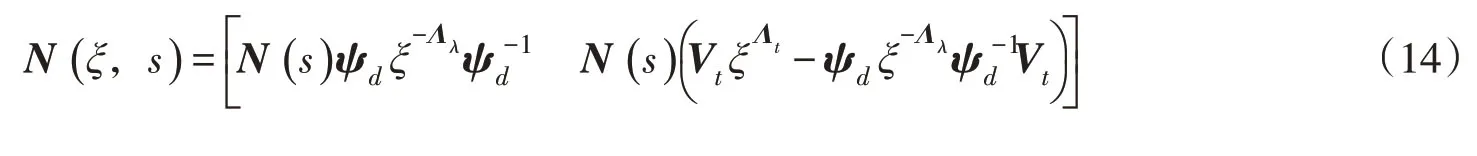
分别令：

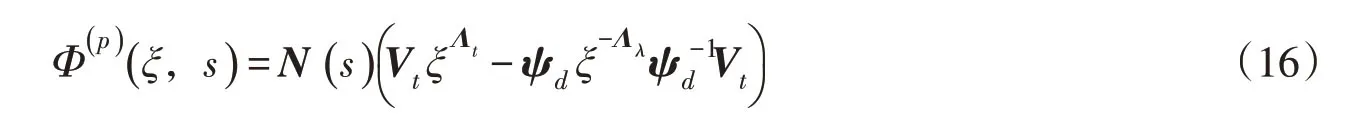
则：

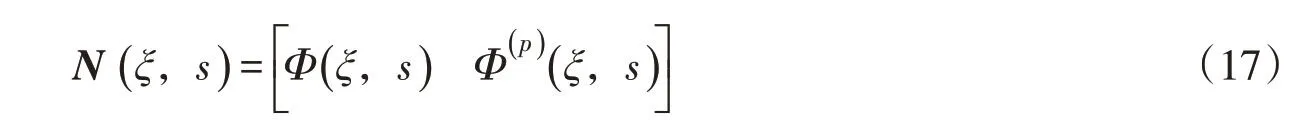
其中，Φ(ξ，s)为不考虑侧面荷载的标准比例边界元形函数[17]，其在单元内部是连续的，如果在相邻单元上有共同的单元边界，那么在单元边界上也是连续的。

矩阵Λλ包含有值为0与-1的特征值，该特征值可以反映出结构的刚体位移和常应变[18]。

式（15）、式（16）共同组成了考虑侧面任意荷载时的形函数。从式（17）中可看出，无侧面荷载的形函数Φ(ξ，s)为考虑侧面荷载的形函数N(ξ，s)的一个特例，即当式（8（c））中待定参数a=0 时：

Φ(p)(ξ，s)可看作是由侧面荷载对位移模式的影响，可将其看作附加位移项。由式（16）可看出，当ξ=1时：

即在单元边界结点上取值为0，Φ(p)(ξ，s)对结点位移没有影响，只对单元内部的位移起了调整作用，因此式（8（c））中的u0中的a可看作为附加的单元无结点位移项，为单元内部自由度。有限单元法中的非协调元[19]通过在单元的位移插值函数中附加无结点的位移项来提高单元的精度，其单元位移插值表示为：

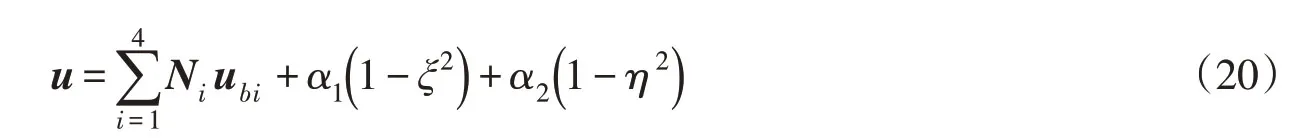
其中，Ni为有限元常规形函数，即：

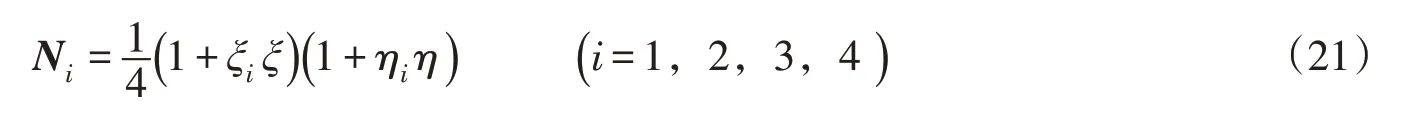
写成矩阵形式为：

其中：

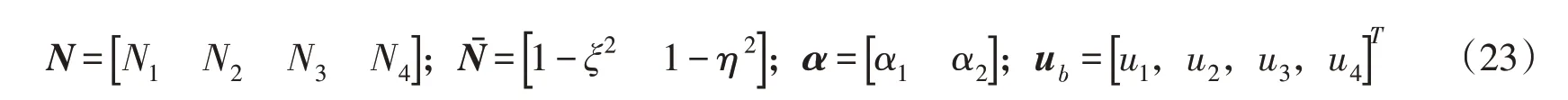
从式（22）中可看出，本文SBFEM 考虑侧面荷载的形函数与非协调元的位移插值函数较为相似，即皆在单元的位移插值函数中添加无结点的位移项，但是从式（20）可看出，非协调元在单元之间的交界面上，附加位移项呈现抛物线形式变化，不能保证单元交界面上位移具有连续性，需要采取很多手段来弥补该问题[20-21]。而由式（19）可知，在单元边界上Φ(p )(ξ，s)引起位移为0，自然满足单元交界面连续性，无需任何手段来解决单元交界面不连续问题。

本文分别给出了六结点、八结点Φ(ξ，s)、Φ(p )(ξ，s)的图形，如图2所示。图2（a）（b）分别给出了六结点、八结点Φ(ξ，s)的图形，代表一个边界节点的单位位移对整个单元内位移的影响。该图形与文献[17]中标准比例边界元形函数的图形是一致的。图2（c）（d）分别为六结点、八结点Φ(p )(ξ，s)的图形，代表侧面均布荷载对单元内位移的影响，由图中可看出，在单元内部，Φ(p)(ξ，s)引起的位移具有连续性，在单元边界上，Φ(p)(ξ，s)引起的位移为0。为了更好的表示Φ(p )(ξ，s)，图2（e）（f）分别给出了六结点、八结点Φ(p )(ξ，s)的平面图。

通过分析可知，考虑侧面荷载的形函数N(ξ，s)由无侧面荷载的形函数Φ(ξ，s)以及由侧面荷载引起的Φ(p )(ξ，s)两部分组成，不考虑侧面荷载的形函数可看作为本文考虑侧面荷载形函数的一个特例，因此将N(ξ，s)称为SBFEM广义形函数。

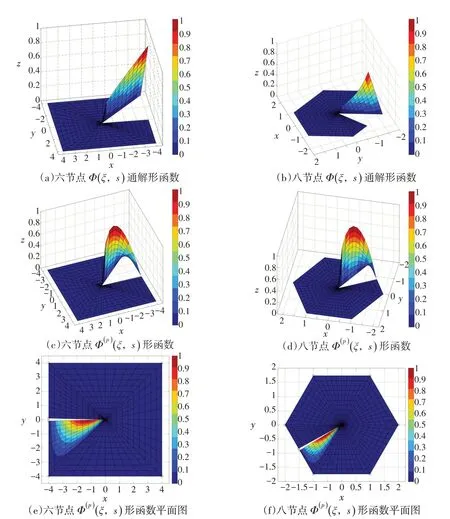
图2 形函数云图

采用与有限元相似方法，将该形函数代入虚功原理，通过计算，可得出考虑侧面荷载存在的比例边界有限元平衡方程：

式中：K为比例边界有限元刚度矩阵；F为比例边界有限元等效荷载。式（24）详细推导过程可见文献[17]。

本文采用多边形单元网格进行数值模拟。多边形SBFEM网格的优点为：对于大型或者复杂结构都可以自动生成满足SBFEM条件的多边形网格，且在裂纹扩展过程中，整体的多边形网格不变，只需对裂纹扩展的单元进行局部网格重划分即可。多边形网格局部重剖分详细过程可见文献[22]。

3 基于混凝土黏聚裂纹模型的SBFEM裂纹扩展模型

Hillerborg 等[1]基于混凝土具有应变软化以及裂尖附近存在黏聚力的特点，提出了著名的虚拟裂纹模型。在含有裂纹的结构内，当裂纹面的张开位移COD和裂纹滑动位移CSD较小时，该裂纹面内之间还具有一定的相互作用，存在着黏聚力，因其尚未发展成真正的宏观裂纹，将其称为虚拟裂纹，虚拟裂纹面构成了断裂过程区（Fracture Process Zone，FPZ）。随着裂纹的发展，当裂纹面张开位移及滑动位移超过一定限值时（wc及sc），虚拟裂纹发展为真正的宏观裂纹。

断裂过程区内黏聚力的正应力分量σ(x)可采用由σ-COD双线性或是单线性软化曲线决定。黏聚力的切向分量τ(x)则可假设为τ-COD的反对称关系[14]。具体如图3所示。

因此裂纹面法向力tn、切向力ts可以根据相对法向位移w及相对切向位移s表示为：

式（25）中黏聚力的方向为裂纹面的法向及切向方向，需要通过坐标变换，将其转换为笛卡尔整体坐标系下的黏聚力：

式中α为裂纹面与x轴的夹角。

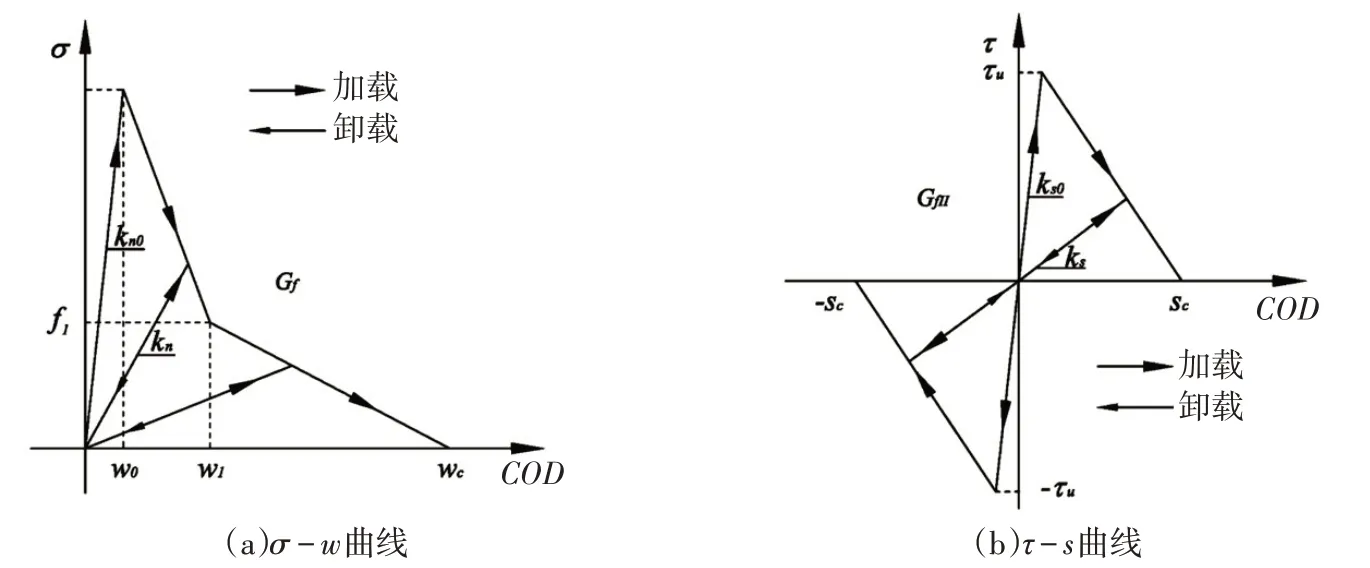
图3 断裂过程区的应力软化曲线[14]

对于黏聚裂纹的分析，Yang 等[14]提出插入界面单元来模拟断裂过程区的黏聚力，在裂尖单元，如图4（a）所示，由于SBFEM在裂尖处没有节点，无法直接和界面单元耦合，Yang等[14]提出了背景域（Shadow Domain）的方法，如图4（b）所示，需要将裂尖单元划分为两个独立单元S1和S2，同时生成两个节点O点和A点，在此基础上，插入界面单元BOC，对SBFEM和FEM进行了耦合。

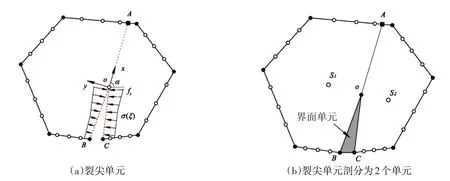
图4 断裂过程区的应力软化曲线

朱朝磊等[16，23]对黏聚力的施加方法进行了改进，通过引入线性渐进叠加假设，对混凝土的裂纹扩展进行了研究，线性渐进叠加假设塑性变形为零，在相同材料及几何尺寸下，不同的裂纹长度的构件具有一系列的线弹性点，荷载-COD曲线可以看作为线弹性点的一条包络线。该方法不需要与有限元耦合和插入界面单元，简化了计算。在计算过程中，需要将裂纹面黏聚力分为裂尖单元的侧面荷载以及非裂尖单元边界荷载，裂尖单元需要通过比例边界有限元（SBFEM）特解的形式进行计算，而非裂尖单元采用标准的SBFEM进行计算，即该计算过程需要分为裂尖单元以及非裂尖单元两种不同模式进行求解。通过计算，得到了与试验及其他数值方法相吻合的结果。

本文在扩展模拟中也采用线性渐进叠加假设，在每一扩展步中，断裂过程区的黏聚力可分为裂尖单元的侧面荷载以及非裂尖单元的边界荷载，根据SBFEM广义形函数方法，以等效节点荷载形式统一施加在节点上，将裂纹面上的边界荷载以及侧面荷载统一于式（24）的右端项，相较于文献[16，23]方法，进一步简化了计算过程。

4 黏聚裂纹开裂准则

考虑混凝土的断裂过程区，可以认为裂纹尖端的应力强度因子值是由外荷载和黏聚力共同作用下的结果：

式中：KⅠcoh为黏聚力作用下的Ⅰ型应力强度因子；KⅠext为外力作用下的Ⅰ型应力强度因子。

由于混凝土中断裂过程区的存在，裂纹尖端奇异性消失，即KⅠ=0；当外力引起裂纹的张开时，即KⅠext＞0 时，黏聚力趋使裂纹闭合，即KⅠcoh＜0；在外力与黏聚力互相作用过程中，会存在一个临界状态，即KⅠ=0，因此可以采用KⅠ≥0 作为判断裂纹扩展的依据[14]。

Moës等[24]指出，混凝土中裂缝的开裂路径对尺寸效应没有荷载位移曲线那么敏感，故混凝土非线性裂纹扩展方向可采用线弹性断裂力学进行判定，扩展方向为：

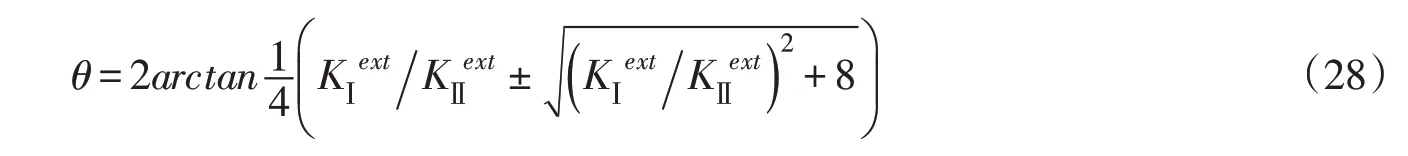
式中KⅠcoh为外力作用下的Ⅱ型应力强度因子。

5 混凝土裂纹扩展计算步骤

本文采用SBFEM广义形函数方法，采用黏聚裂纹模型对混凝土的非线性断裂扩展进行模拟，具体步骤包括：（1）设定裂纹扩展步长Δa，在每一扩展步中，设定外荷载增量步Δp，外荷载设置从0开始计算，经过n个荷载步，外荷载P=nΔp。（2）在每个荷载步中，根据图3所示的应力软化曲线可看出，裂纹面内的黏聚力是与裂纹面相对位移相关的，因此需要通过迭代方法求解黏聚力：①首先假设结构只受荷载P作用，通过SBFEM广义形函数方法求解得到裂纹面相对位移，根据应力软化曲线得到相对应的黏聚力；②将黏聚力与外荷载共同作用于结构上，再一次通过SBFEM广义形函数方法求解得到裂纹面相对位移，然后得出相对应的黏聚力；③重复②的求解过程，直至求解出的黏聚力以及裂纹面相对位移与上一迭代步中求解的结果相对误差小于设定的限值，则视为完成了该步骤，得到了相应的黏聚力。（3）在该外荷载下，通过式（27）计算应力强度因子，若不满足，则继续增大外荷载P，直至满足KⅠ≥0 后裂纹扩展。（4）采用多边形网格重划分技术进行网格重剖分来实现裂纹的扩展，扩展方向通过式（28）线弹性断裂力学方法判定。（5）重复步骤（1）—（4）对混凝土进行非线性扩展，直至结构失稳破坏。

6 数值算例

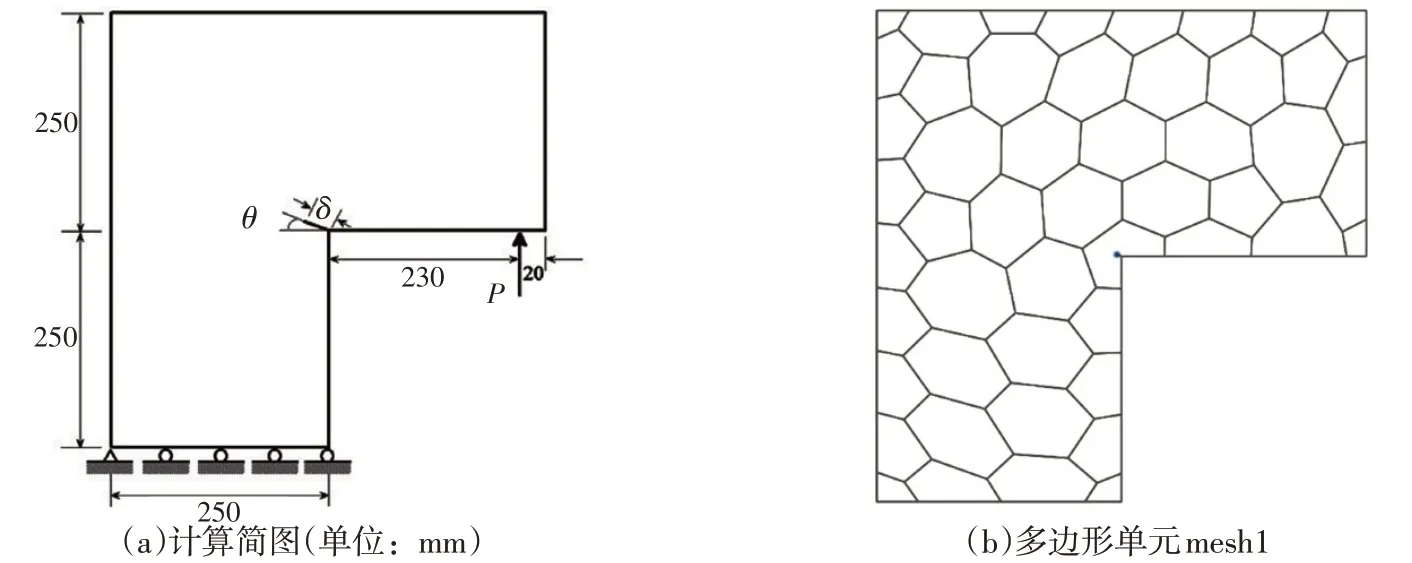
图5 L型板及多边形单元

6.1 含预设初始裂纹的L型板含有预设裂纹的L型混凝土板，模型的几何尺寸、边界条件如图5所示，该板的初始裂纹长度δ=5 mm，裂纹的角度θ=20°，板在右侧受到竖直向上的集中荷载P的作用。其材料参数为：弹性模量E=20 GPa，泊松比ν=0.18，抗拉强度ft=2.5 MPa，断裂能为Gf=130 N/m。采用双线性软化[25]曲线模型来模拟黏聚力，板的厚度为100 mm，计算过程中采用平面应变假定。该模型被划分为50个均匀的多边形单元mesh1，如图5（b）所示。

图6给出了该板的裂纹扩展过程及黏聚力分布，从图6可看出，在荷载达到峰值（P=7.375kN）之前，裂纹的断裂过程区得到了扩展，而真实裂纹并未扩展。当混凝土发展到软化阶段，在P=5.25kN时，裂纹口处的黏聚力为0，说明裂纹开始真正的扩展，随着进一步的发展，断裂过程区逐渐缩短，而真实裂纹长度逐渐增大。

在裂纹的扩展的过程中，断裂过程区的黏聚力位置以及分布也是逐渐变化的，在荷载峰值及峰值前阶段，由于裂纹法向及切向张开位移较小，裂纹面黏聚力分布较大，而在软化阶段，由于裂纹法向及切向张开位移的增大，裂纹面的黏聚力分布迅速减小，仅在裂尖附近区域内存在黏聚力。

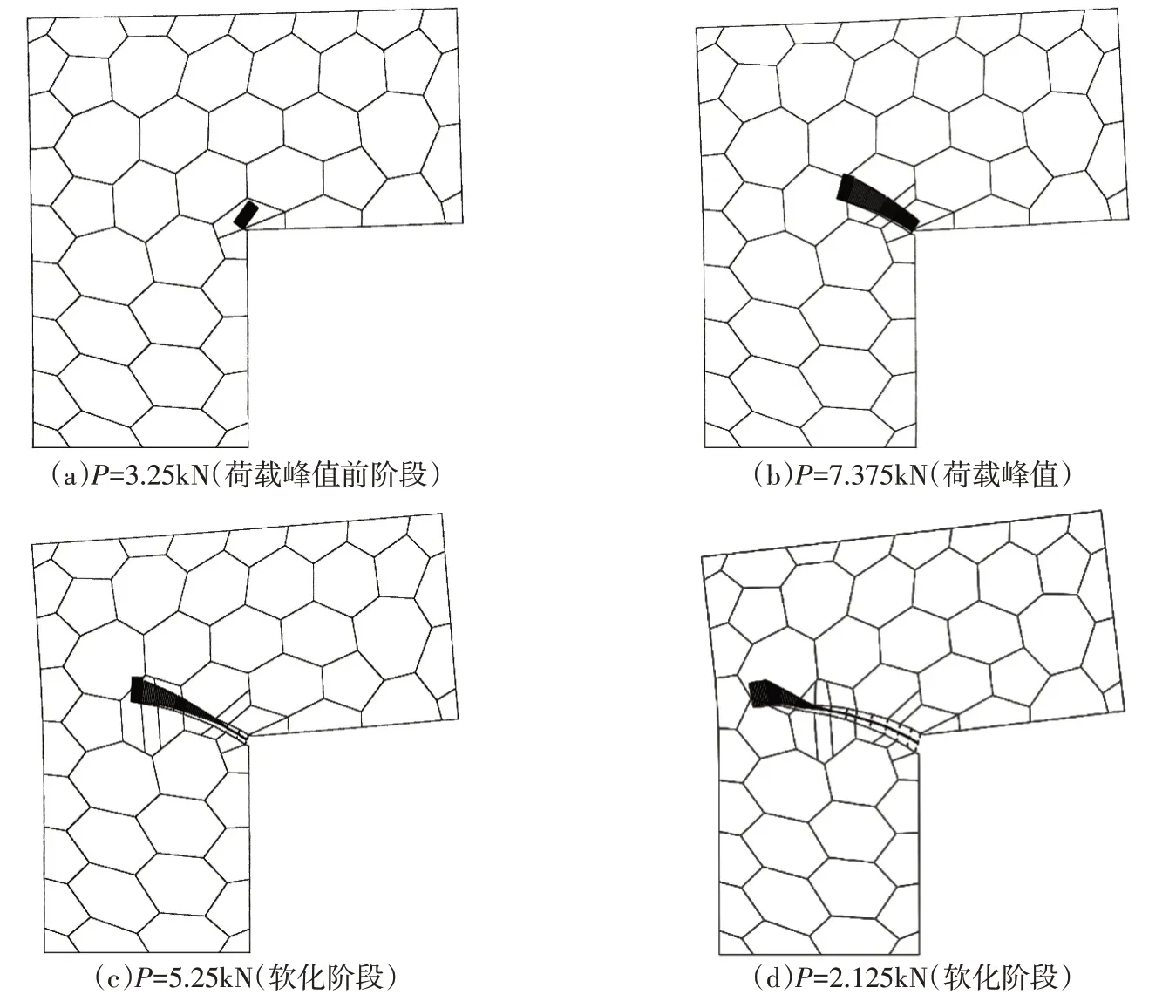
图6 裂纹扩展过程及裂纹黏聚力分布

为了研究SBFEM 方法对于网格的依赖性，本文还分别采用了如图7所示的中等网格mesh2（128个单元）以及细网格mesh3（331个单元），对该板进行混凝土黏聚裂纹扩展模拟。

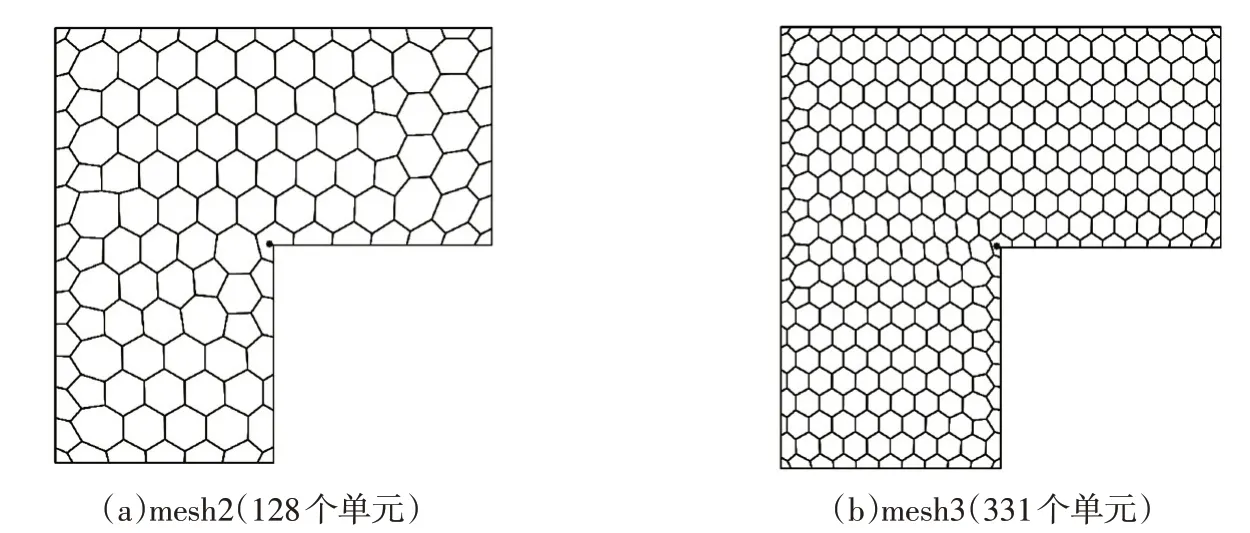
图7 逐渐加密的多边形网格

图8分别给出了mesh1、mesh2、mesh3三种不同密度网格的荷载与施加荷载处的位移关系曲线。从图8可看出，粗网格mesh1在位移为0.185 mm处取得荷载峰值7.375 kN，细网格mesh3在0.190 mm处取得荷载峰值7.375 kN，粗网格与细网格之间的计算结果基本没有差别，该结果与Ooi等[25]的模拟结果也基本一致。

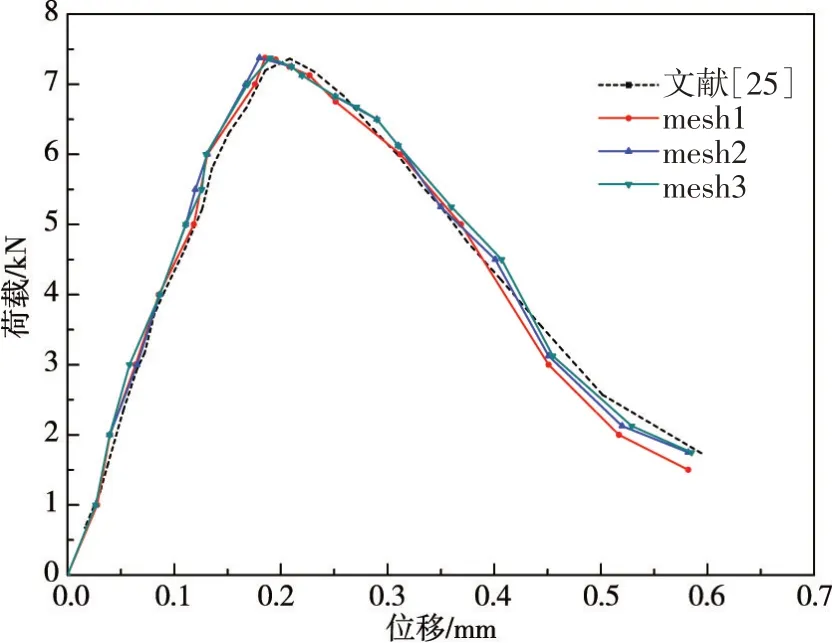
图8 荷载-位移曲线

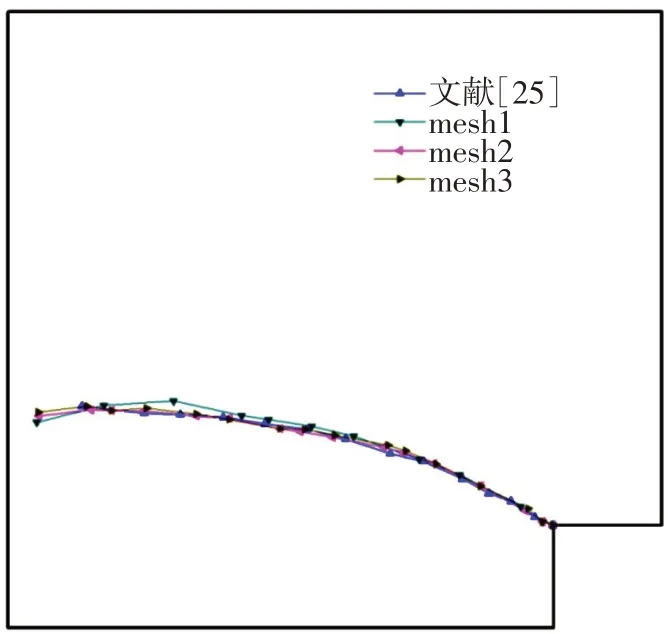
图9 裂纹扩展路径（局部放大图）

图9给出了三种不同网格密度的裂纹扩展路径。由图9可以看出，采用不同的网格的扩展路径基本一致，都是沿着初始裂纹方向倾斜向上发展，在扩展后期裂纹方向趋近于水平方向。这说明，由于SBFEM在处理裂纹问题时的独特优势，预测得到的荷载曲线以及裂纹路径对网格的粗细程度不敏感，仅采用较粗的网格就能够模拟得到准确的数值结果。

6.2 四点剪切梁含有一个预设初始裂纹的四点单边缺口剪切梁，Arrea[26]曾对该剪切梁进行了试验分析，该剪切梁模型成为非线性断裂力学的一个经典算例。图10（a）给出了梁的几何尺寸、边界条件以及材料参数。本文采用Ooi等[27]模拟给定的材料参数：弹性模量E=24.8 GPa，泊松比ν=0.18，板的厚度为152 mm，抗拉强度ft=4 MPa，断裂能Gf=0.15 N/mm。采用线性软化曲线模拟黏聚力，计算过程中，采用平面应力假定。如图10（b）所示，采用58个多边形单元进行网格划分，裂纹扩展步长Δa=20mm。

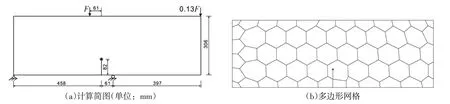
图10 含预设初始裂纹的四点弯梁

图11为裂纹扩展路径及黏聚力分布。从图11可看出，在荷载达到峰值前，断裂过程区得到了发展，而真实裂纹并未扩展。当混凝土发展到软化阶段，在F=105.9 kN时，裂纹口处的黏聚力为0，真实裂纹发生了扩展，随后断裂过程区逐渐缩短，而真正的裂纹长度逐渐变长。

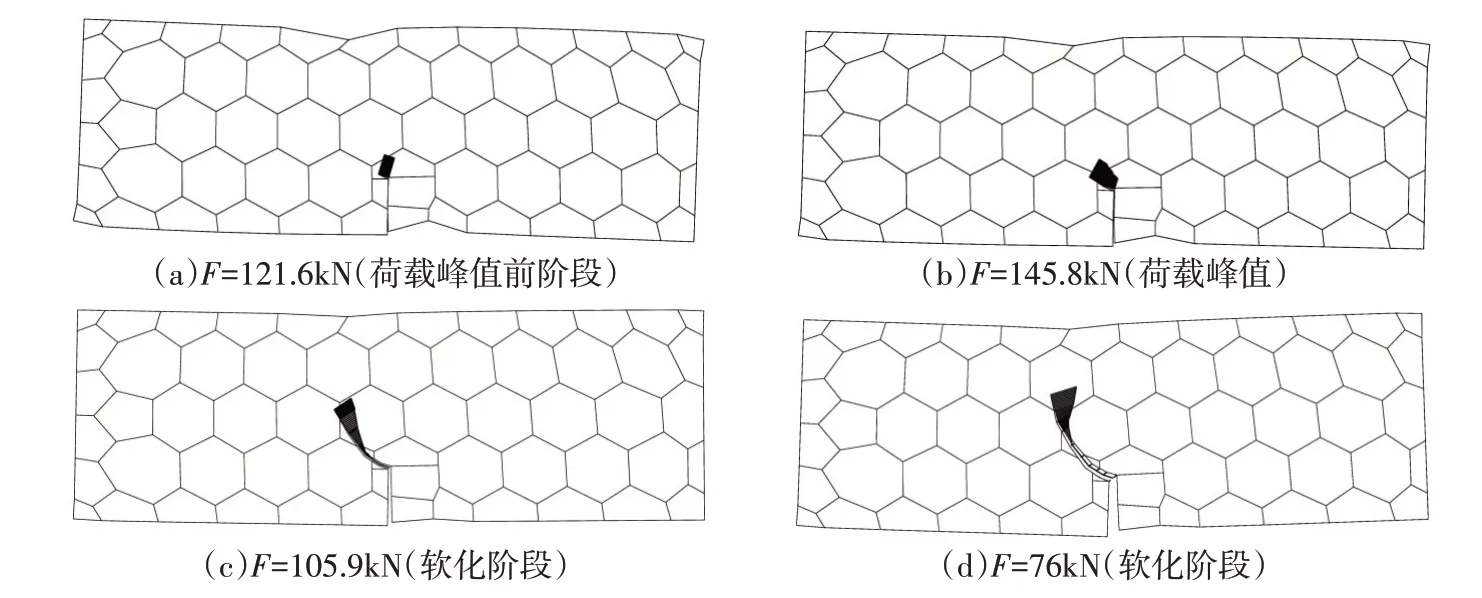
图11 裂纹扩展路径及黏聚力分布

为研究不同的裂纹扩展步长对裂纹扩展路径的影响，本文分别采用Δa=20、25和30mm对该剪切梁进行了扩展模拟。图12给出了荷载与裂纹口处的滑移位移（CMSD）曲线。从图12可看出，不同的裂纹扩展步长对荷载-CMSD的影响较小，在荷载峰值前结果几乎一致，只是在软化阶段，有较小的区别，这说明选取不同的裂纹扩展步长对模拟结果的影响不大。该方法与Arrea[25]采用试验方法得到的曲线及Ooi 等[27]采用SBFEM-FEM耦合方法模拟得到的曲线基本一致。

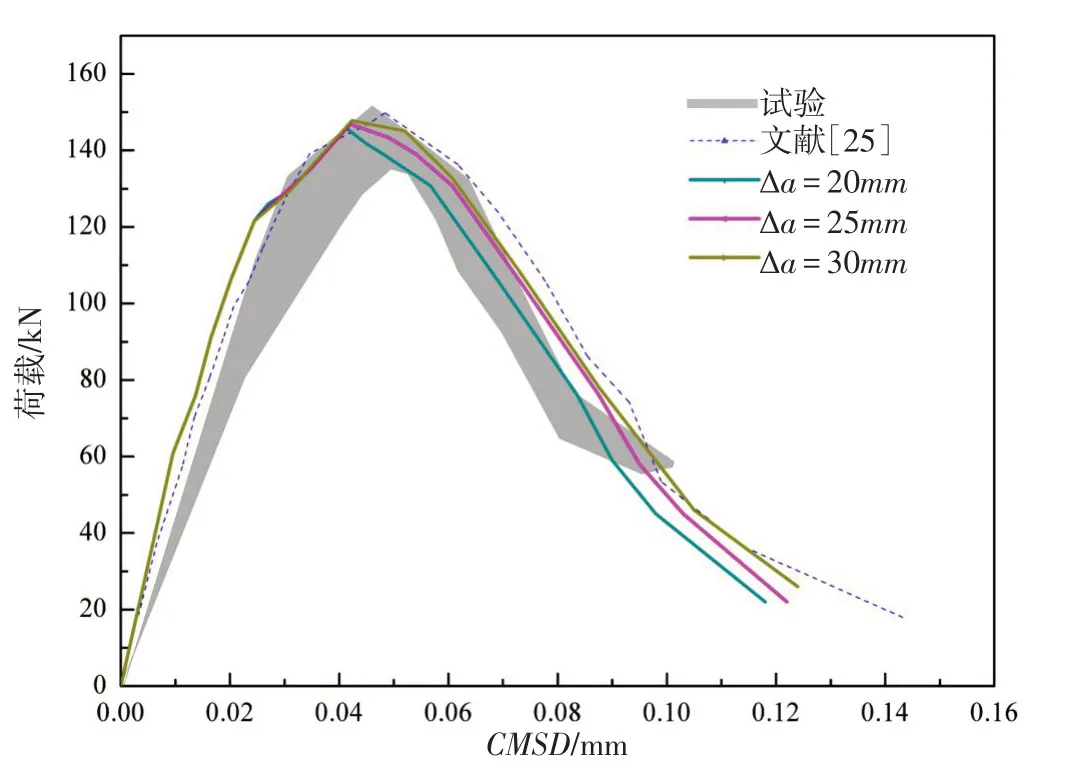
图12 荷载-CMSD曲线

7 结论

本文基于比例边界有限元法解的形式，给出了侧面在任意荷载下的比例边界有限元的广义形函数，进一步阐述了该方法具有自然满足单元交界面连续性的优点。基于该方法，建立了混凝土非线性裂纹扩展模型，在断裂过程区，虚拟裂纹面的黏聚力（分为非裂尖单元的边界荷载以及裂尖单元的侧面荷载）采用形函数以等效荷载的形式统一直接施加在单元节点上，不需要耦合界面单元或者采用特解形式求解，简化了计算过程，并给出了计算步骤以及求解与裂纹面张开位移相对应的黏聚力的迭代方法。最后两个不同数值算例的研究表明，该模型可以准确且有效地模拟混凝土非线性裂纹扩展问题。