BRR-SVR月降水量预测优化模型

贺玉琪，王 栋，王远坤

（南京大学 地球科学与工程学院，江苏 南京 210023）

1 研究背景

受地形和气候等诸多因素影响，降水时间序列多由趋势项、周期项和随机项混合叠加而成，兼有长短期变化规律[1]。传统的时间序列预测方法如简单平均法、指数平滑法等对数据的平稳性有较高要求，不适用于预测非平稳水文时间序列。神经网络（ANN）方法常用于水文时间序列分析[2-5]，但在设置复杂网络参数和结构的固定学习速率下，网络收敛速度较慢[3]，训练容易陷入局部最小值，导致学习失败[4]，这些不足限制了ANN的应用。支持向量机回归（Support Vector Regression，SVR）也常用于时间序列的研究[1，6-10]，SVR遵循结构风险最小化原则[7]，其拓扑结构由支持向量决定，避免了拓扑结构难以确定的问题[8]，最终化为求解线性约束的凸二次规划优化问题[11]，因此可得全局最优解。贝叶斯岭回归（Bayesian Ridge Regression，BRR）方法假设参数服从高斯分布，在估计过程中自动引入正则项，解决了过拟合问题[12]，且BRR适合解决小样本高维度问题，明显优于ANN方法。BRR方法曾被用于降水资料时间序列的构建，并体现一定的优越性[13]。

小波变换可将时间序列分解到不同的时间尺度，反映数据在不同分辨率水平上的变化规律[15]，已被广泛用于水文过程的多尺度分析研究[15-18]。以往研究中，小波分解后的各子序列采用相同模型，由于各序列的数据变化规律不同，在一些序列上SVR的精度较高，而BRR更适合另一些序列。本文针对这一点，提出不同子序列采用不同模型进行回归，利用校验数据从SVR和BRR中选择对各子序列预测精度更高的模型，构建BRR-SVR优化模型，根据国内外文献调研结果，该优化模型尚未用于水文及其他领域的研究。相比于单一的BRR和SVR模型，BRR-SVR模型能够充分利用小波变换的优势，由于最终的预测结果是由不同序列的预测结果叠加而得，优化模型保证了每个子序列上的预测误差最小，使得整体预测精度最大。

2 基本方法

2.1 小波变换小波是一种长度有限、平均值为零的波形。小波函数通过伸缩与平移变换形成灵活可变的时频窗进行局部化分析[5]。小波变换分为连续小波变换和离散小波变换，水文序列多为观测的离散值[17]，因此采用离散小波变换。设离散信号f(n·Δt)为一个平方可积函数，其离散小波变换为：

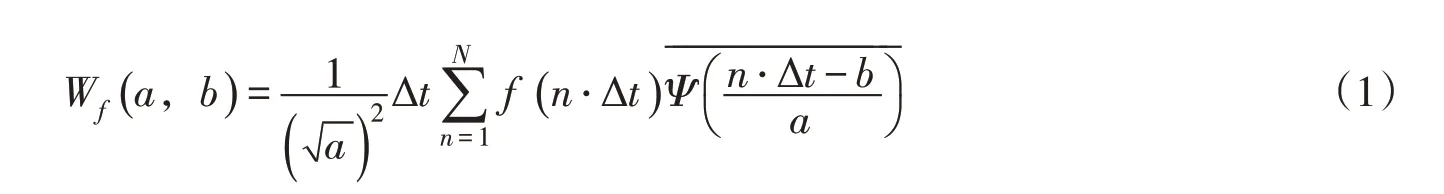
式中：W f(a，b)为小波变换系数；a为尺度因子；b为平移因子；Ψ(t)为小波母函数；Ψ-- -- (-t-)为Ψ(t)的复共轭函数；Δt为采样时间间隔；n为样本总数。

对原始序列X，使用Mallat算法进行分解和重构，Mallat算法是一种针对小波系数进行逐层分解和重构的小波变换算法[19]。原序列经第一次分解得到一个低频序列a1和高频序列d1，之后的每层分解均是将上一层的低频信号aj-1分解成一个低频序列aj和高频序列dj，长度减半。对最大分解水平上的低频序列ak和各高频序列d（jj=1，2，…，k）通过小波逆变换进行重构[5]，得到重构序列Ak和D（jj=1，2，…，k）。各重构序列的长度与原序列相等，原序列可由各重构序列叠加而得，对于序列X有：

2.2 支持向量机回归（SVR）支持向量机（SVM）是根据结构风险最小化原理提出的一种机器学习算法，其基本思想是用核函数将原样本空间中的非线性回归转化为高维空间中的线性回归[9]。SVM 包括支持向量机分类和支持向量机回归，SVR的原理如下。

给定样本{(xi，yi)，i=1，2，…，m} ∈R n，m为样本个数，n为样本维度，回归函数为：

式中：φ(x)为R n到高维特征空间的非线性映射；ω为超平面的权值向量；b为偏置。

根据结构风险最小化原则，原问题转化为在式（5）所示的约束条件下由式（4）求出最小值：

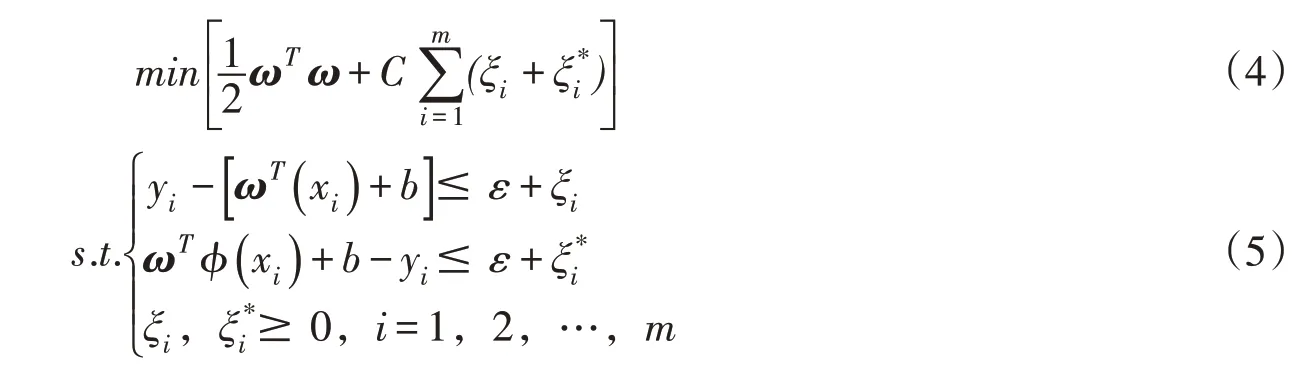
式中：常数C为误差惩罚因子；m为样本容量；ξi、ξ*i为松弛变量；ε为不敏感损失系数。

引入拉格朗日乘子，可以得到上述优化问题的对偶问题：

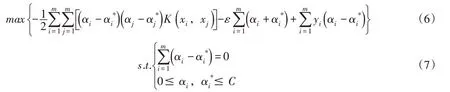
式中：αi、αi*、αj、αj*为拉格朗日乘子；K(xi，xj)为核函数。由于最后化为一个线性约束的凸优化问题，所以解具有全局最优性和唯一性[20]。

2.3 贝叶斯岭回归（BRR）BRR是以贝叶斯理论为基础的一种机器学习回归算法[21]。贝叶斯线性回归的函数见式（8），其目的是求使得损失函数式（9）最小的参数向量分布。

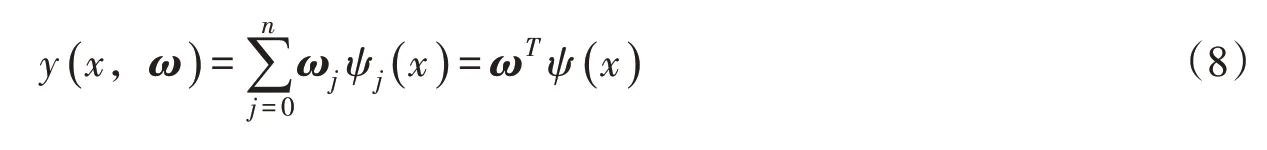
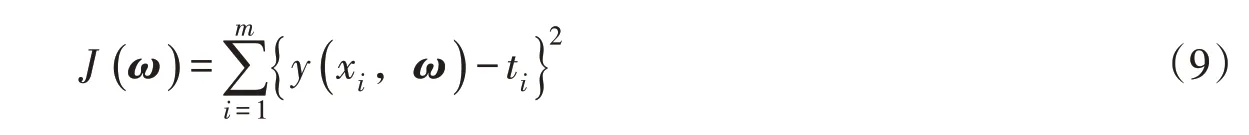
式中：n为样本空间维度；m为样本容量；ω为参数向量；Ψ(x)为输入向量x的非线性函数，其中Ψ0(x)=1；ti为观测值，ti =y(xi，ω)+ε，ε为噪声，假定ε和ω分别服从高斯分布和则t是以y(x，ω)为均值的高斯分布，t的类条件概率密度函数为式（10），ω的先验概率为式（11）：

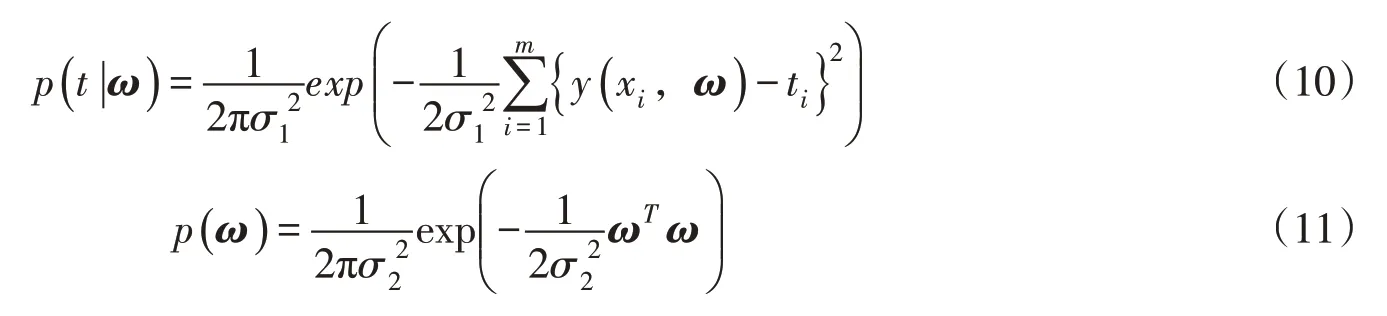
依据贝叶斯规则有：

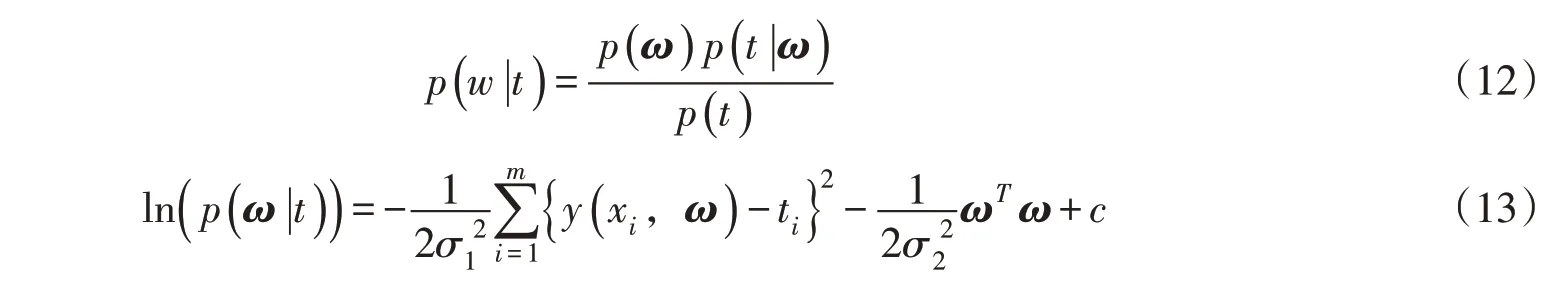
式中：p(ω|t)为后验概率；p(t)为与ω无关的常数；c为常数，先验概率对应岭回归中的L2 正则项，因此称为贝叶斯岭回归。

BRR在估计过程中自动引入正则项，最终得到的是参数的后验分布，避免了极大似然估计中的过拟合，得到更精确的参数估计。

3 模型构建

模型的构建分为数据预处理、模型的训练和校验，具体流程见图1。在模型的校验阶段，需要评价模型的预测性能，本文采用确定系数R2、平均绝对百分比误差MAPE和平均绝对误差MAE这3项指标作为评价模型性能的依据，计算公式如下：

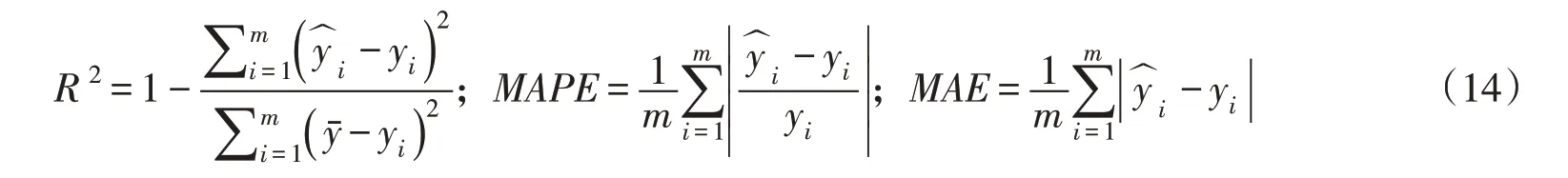
式中：yi为预测值；yi为观测值；y为观测值的平均值；m为样本总数。R2越接近1，预测值与实测值越吻合，MAPE和MAE越小预测精度越高。

3.1 数据预处理不同月份的降水数据存在极端值和较多噪音，波动频繁，经过中心化处理可避免异常值和极端值的影响，减小误差，加快模型训练速度。中心化公式为：

式中：xt为t时刻降水量，mm；μ为整个时序降水均值，mm；σ为对应的标准差。

对中心化处理后的数据进行小波分解和重构。本文选用Daubechies 小波族的“db3”正交小波和Mallat算法对数据做5层分解与重构，得到一组低频序列A5和5组高频序列D（jj=1，2，…，5）。

为了适应支持向量机回归和贝叶斯岭回归的分析方式[22]，对各子序列进行相空间重构，将一维序列转换为二维矩阵。将前m月的降水量作为输入，下个月的降水量作为输出。时间序列{xt，t=1，2，…，n}经过相空间重构后可得样本：Xi ={xi，xi+1，…，xi+m-1}，Yi =xi+m，i=1，2，…，n-m，样本量为（n-m）。

对6组子序列做相同的相空间重构，将重构后的样本进行划分，按时间先后顺序分为训练数据、校验数据和测试数据。训练数据用于模型学习历史数据的规律；校验数据用于参数的调整和选择最优模型；测试数据用于评估模型的预测性能。训练数据和校验数据都参与了模型的构建，而测试数据对于模型是全新的数据。

3.2 模型的训练和校验由2.1节可知，最终的预测结果由6组子序列的预测结果叠加而得，若要整体的预测精度最大化，需要对6 组子序列分别建模，确保每个子模型的预测误差最小。用校验数据选取最佳模型，以R2、MAPE和MAE这3项指标来评估模型的精度，遵循少数服从多数的原则，当有两项及以上指标的结果都说明一个模型的精度最高，该模型即为最佳模型。分析发现，用3项指标与仅用确定系数R2得到的结果基本一致，为了提升计算速率，仅用R2作为评价指标。3.2.1 BRR模型 贝叶斯岭回归中主要的超参数有正则化参数α1、α2和λ1、λ2，设置4 个超参数取值范围均为{10-9，10-8，…，10-1}，不同取值的超参数构成多组参数组合，用6组训练数据集在各种参数组合下训练模型，再用相应的校验数据检验所有模型，以R2为评价指标，R2最大时对应的参数组合即为最佳参数，由此确定6个子序列对应的最佳BRR模型。3.2.2 SVR模型 支持向量机回归的主要超参数有C、核函数和多项式的阶数degree，设置C的取值范围为{0.1，1，10，50，100}，degree的取值范围为{1，2，3，…，10}，核函数的取值范围为{‘rbf’，‘sigmoid’，‘poly’}。不同取值的超参数构成多组参数组合。在各种参数组合下训练模型，用校验数据检验所有模型，R2最大时对应的参数组合即为最佳参数，由此确定6个子序列对应的最佳SVR模型。

3.2.3 BRR-SVR模型 在6组子序列已经选取了对应的最佳SVR和BRR的基础上，比较每组SVR和BRR在对应的校验数据上的表现，发现对于高频序列D1、D4、D5和低频序列A5，BRR模型的精度往往高于SVR，而在序列D2和D3上，SVR的精度更高。因此，BRR-SVR的原理是，比较各序列对应的BRR 子模型和SVR子模型在校验数据上的R2值，以R2值更大的模型作为最适合该序列的模型，得到6组子序列的最佳模型，从而构建出BRR-SVR组合模型。由于R2表示预测值与实测值的逼近程度，R2越大代表预测值越接近真实值，因此选择R2值更大的模型能够确保每个子序列的预测值更逼近真实值，以此达到优化的效果。

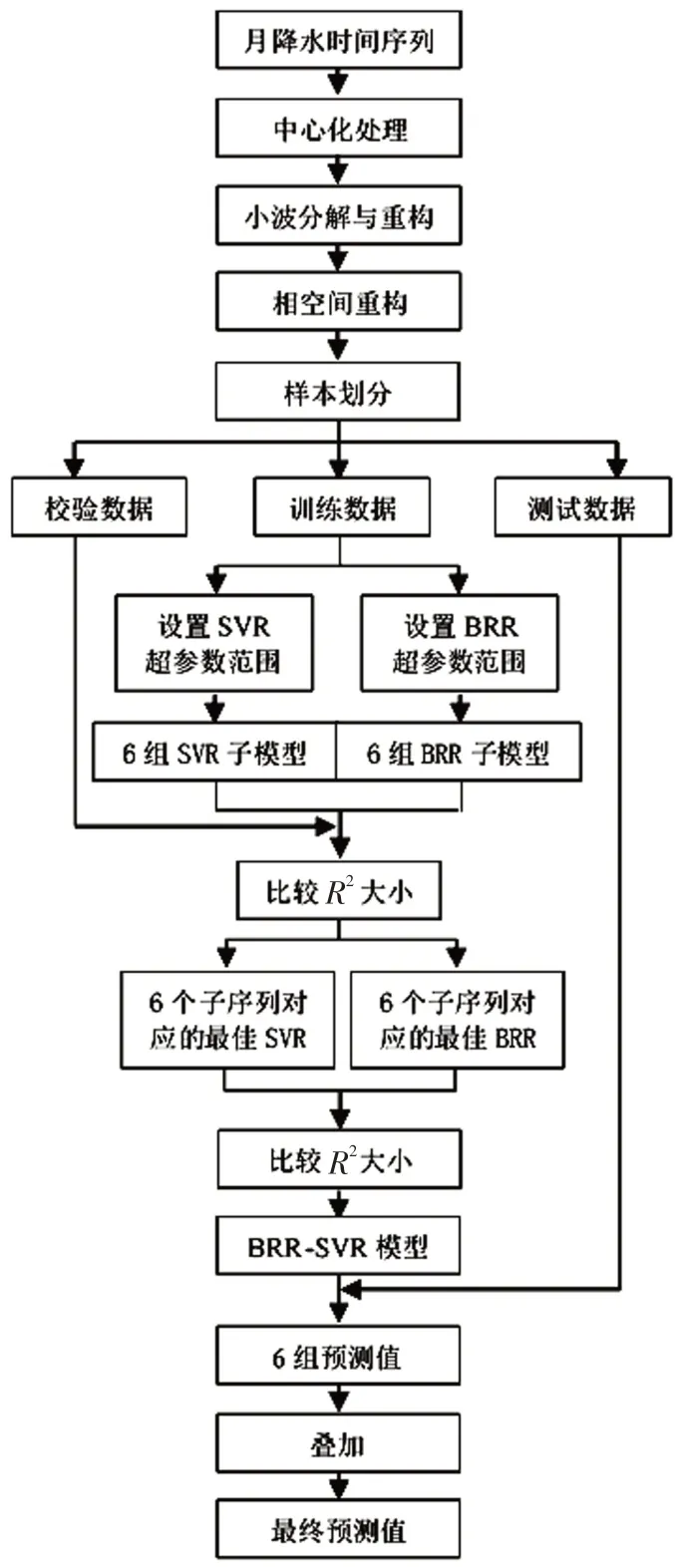
图1 BRR-SVR模型流程图

4 实例分析

以北京站、南京站和7 个太湖流域的雨量站1951—2015年间660 个月的降水资料为例，研究BRR模型、SVR模型和BRR-SVR模型对月降水量的预测性能。9个雨量站的降水数据来源于中国气象数据网1951年1月1日至2015年12月31日的无空缺日降水数据，日降水数据经过累加得到月降水数据。对月降水数据做中心化处理和五级小波分解重构，得到6 组子序列。对所有站点的数据，令m=11，对各序列做相同的相空间重构，重构后每组样本容量为649。为了保证能较好的训练，防止模型对训练数据过拟合，将样本按时间顺序分为训练数据∶校验数据∶测试数据=529∶60∶60。以上过程均通过PC机上的Python3.7编程实现。

4.1 模型参数校验及优化模型组合根据3.2节中的方法对SVR模型和BRR模型进行校验，并选择每组序列的最优模型。不同站点不同序列所对应的SVR模型超参数不同，受篇幅限制，本文只列出北京站和南京站的SVR 超参数取值（见表1）。不同站点的6 组子序列对应的BRR模型超参数几乎一致，故统一设定为α1=10-3，α2=10-8，λ1=10-8，λ2=10-3。最后利用校验数据从最优SVR和BRR中筛选出该序列的最优模型，各站点的模型组合见表2。

表1 北京站和南京站不同序列的SVR超参数取值

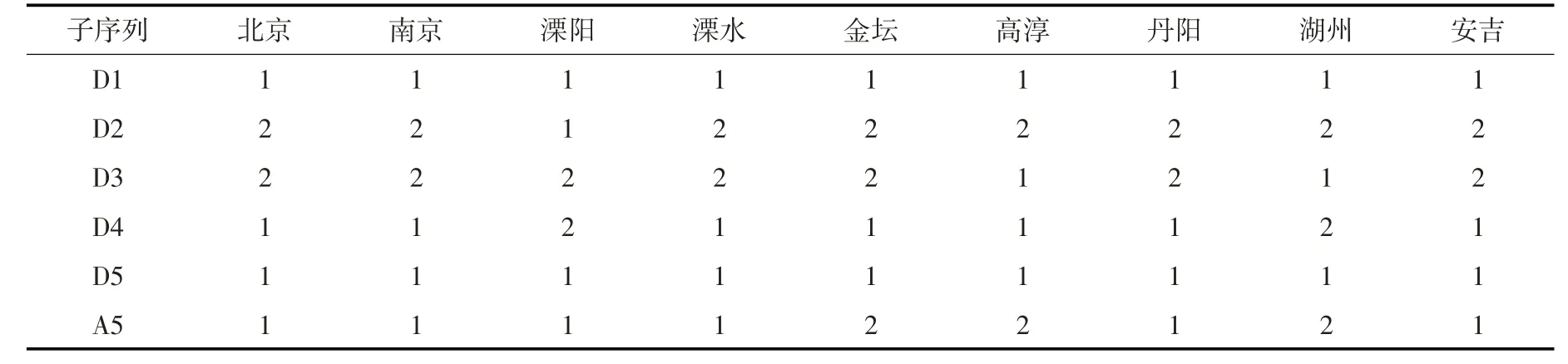
表2 各站点不同序列的模型组合（1-BRR模型，2-SVR模型）

4.2 模型预测效果评价利用校验后的模型对训练期的数据进行拟合，并对校验期和测试期的数据进行预测，3类模型对不同时期降水量的拟合和预测结果见表3、表4和表5。

由表3 可知，对于训练数据，BRR-SVR的拟合精度明显高于BRR和SVR，综合3 项指标来看，SVR对训练数据的拟合能力优于BRR。由表5可知，对于测试数据，同样是BRR-SVR的预测精度更高，但BRR的泛化能力总体上高于SVR。对比训练数据和测试数据上的R2值可知，SVR的拟合精度基本在0.92左右，而预测精度大多在0.82～0.9之间；BRR的拟合精度和预测精度均在0.9左右。对比SVR和BRR 在训练数据和预测数据上的表现可知，BRR的拟合能力稍逊于SVR，但面对新数据，BRR的泛化能力反而更强。

对比表4和表5可知，模型对不同时期的预测精度差异不大。从R2值上来看，BRR-SVR 大多高于0.89，BRR略低于BRR-SVR，对绝大多数站点，SVR模型的精度低于0.89，波动范围较大。从平均绝对百分比误差上看，大体上BRR-SVR＜BRR＜SVR，除了北京站大于2，其他站点基本处于0.2～0.6之间。从平均绝对误差上看，总体满足BRR-SVR＜BRR＜SVR，北京站的MAE值在8.32～12.82 之间，而其他站点的值处于18～30之间。由以上分析可知，3类模型对北京站的预测效果与长江中下游区域的水文站差异较大，北京市为国家重要的政治和经济中心，南京市为长江三角洲区域一体化发展等多个国家战略交汇的中心城市，因此选择具有代表性的南京站和北京站做进一步阐述。

4.2.1 北京站预测效果分析 各模型对北京站2011—2015年间的月降水量预测效果见图2，图中实线为观测值，虚线为预测值。由图2 可知，3 类模型都能较精确的预测下个月的降水量，从直观上看，BRR模型的逼近能力不如另外两类模型。

由表5可知，对于北京站，BRR-SVR与SVR的R2值均为0.966，高于BRR的0.932，从平均绝对百分比误差来看，BRR-SVR的精度最高，其次是BRR，SVR的预测精度最低。从平均绝对误差来看，SVR的精度略高于BRR-SVR，两者均明显高于BRR。由此可知，对于北京站，SVR的预测精度高于BRR，而BRR-SVR模型的预测精度与SVR基本相同，并未体现明显的优越性。

4.2.2 南京站预测效果分析 3类模型对南京站2011—2015年间月降水量的预测效果见图3，由图3可见，3类模型的预测值都能有效逼近观测值，基本捕捉到了南京站月降水量的变化规律。除了2011年3月、2011年8月、2013年1月、2013年12月和2015年3月这几个点的预测值有直观上的差异外，3 者在其他点的预测值没有明显差别。此外，3 类模型对汛期降水量的预测效果要比非汛期更好，这对于城市的防洪建设极为重要。

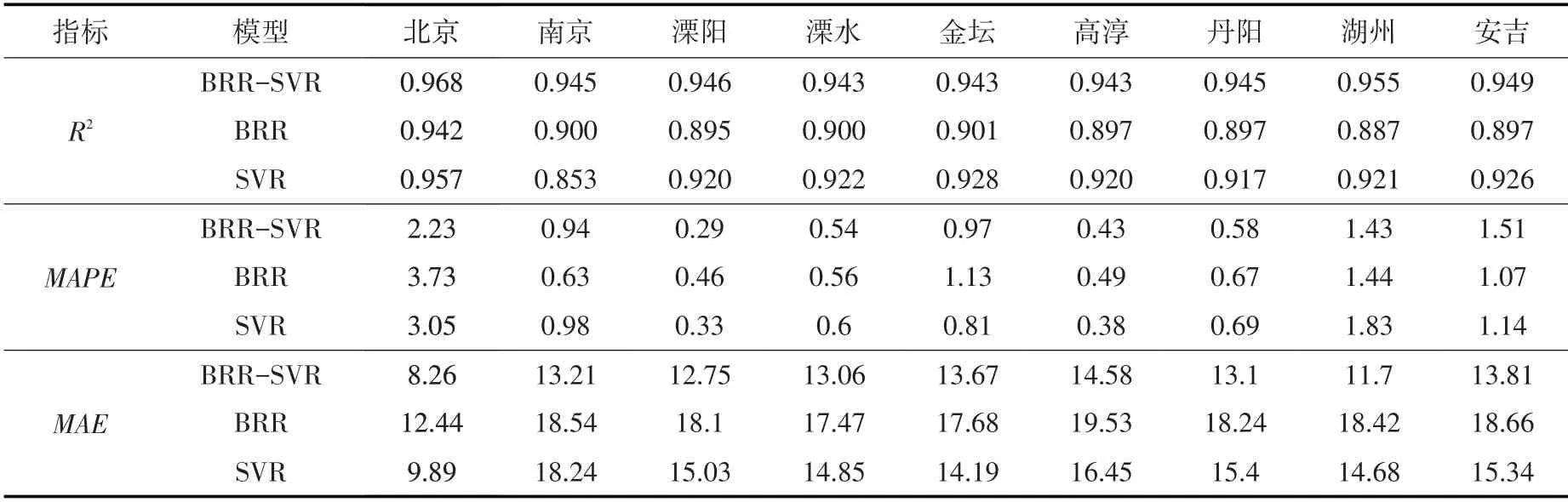
表3 训练期各站点BRR-SVR、BRR和SVR模型拟合精度计算结果

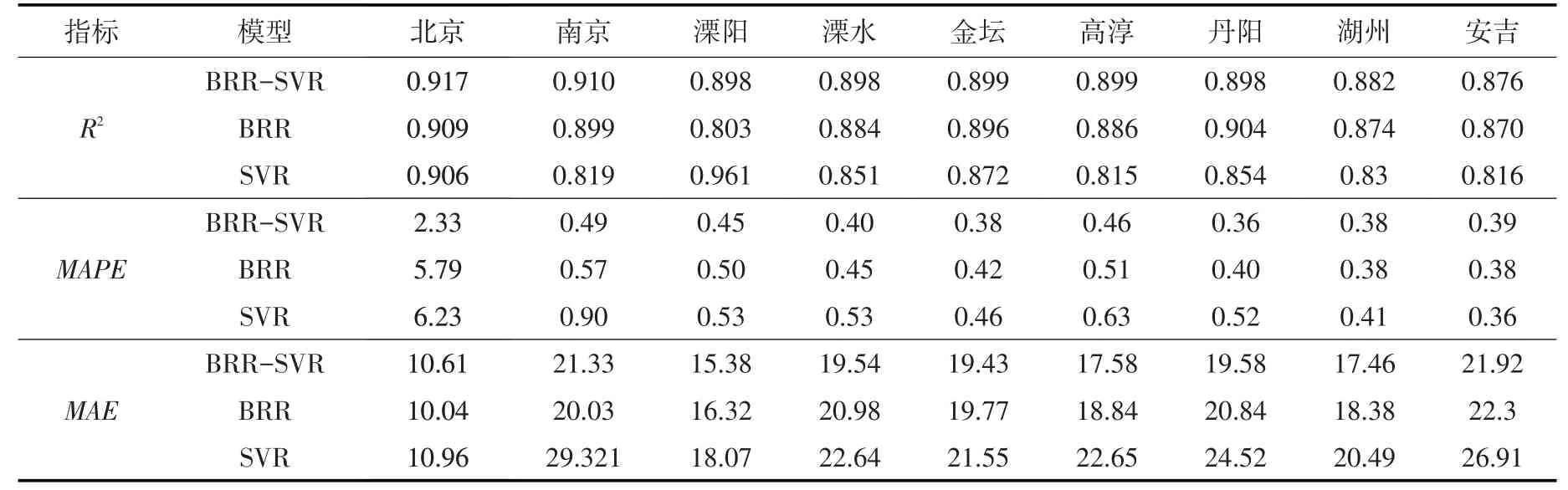
表4 校验期各站点BRR-SVR、BRR和SVR模型预测精度计算结果

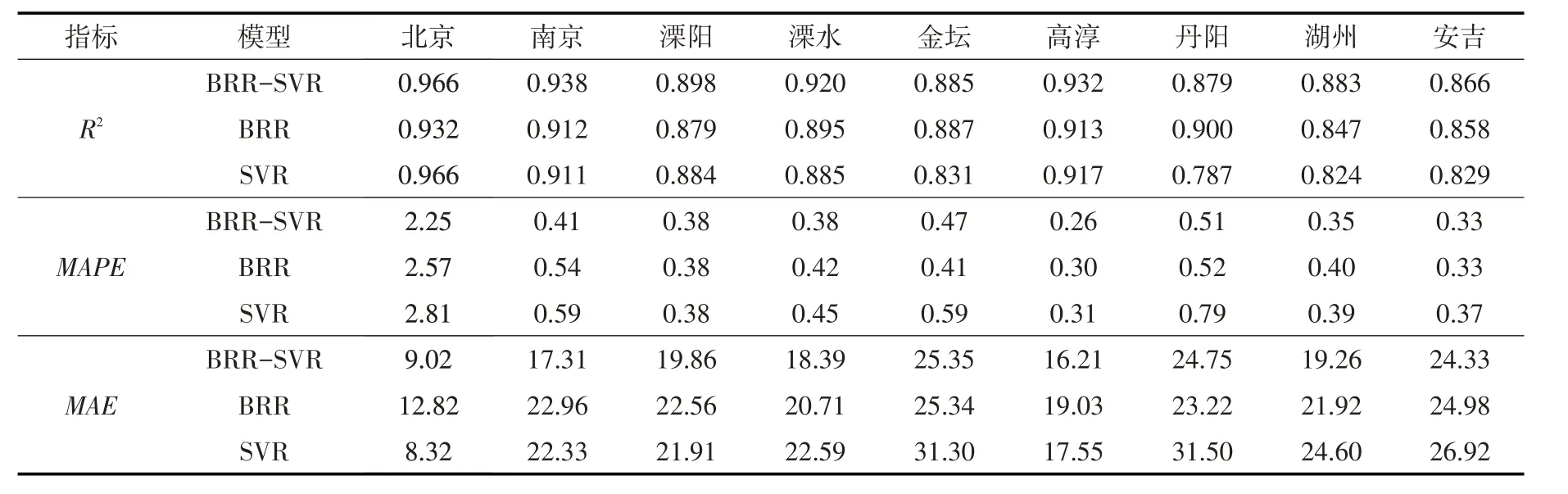
表5 测试期各站点BRR-SVR、BRR和SVR模型预测精度计算结果

由表5 可知，对于南京站，BRR-SVR模型的R2更接近1，平均绝对百分比误差和平均绝对误差都比SVR和BRR 小，可见BRR-SVR模型在南京站上更具优势。相比于SVR，BRR模型的R2更大，平均绝对百分比误差更低，仅在平均绝对误差上表现次于SVR，因此对于南京站，BRR的预测性能要优于SVR。

4.2.3 北京站与南京站预测效果的对比 由4.1节中的分析可知，仅考虑R2值和平均绝对误差的情况下，3类模型对北京站的预测精度高于长江中下游的水文站。以BRR-SVR模型为例，将北京站和南京站的降水量置于同一纵坐标水平下（图4），由图4可见，北京站每年11月至次年2月，月降水量曲线十分逼近横坐标轴，这段期间降水量处于极低的水平，对应的MAPE表达式（15）中的分母几乎为0，导致北京站的平均绝对百分比误差偏大。因此，不考虑MAPE指标的情况下，可以认为模型对北京站的预测精度高于长江中下游。

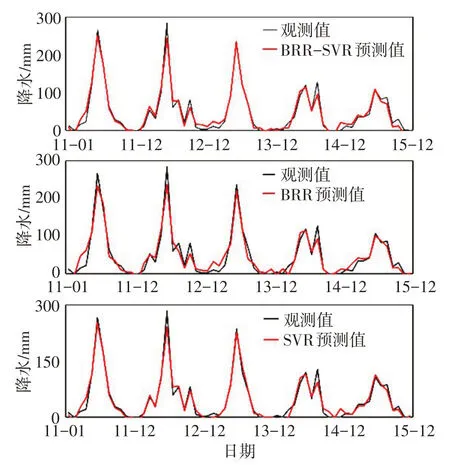
图2 BRR-SVR、BRR和SVR对北京站月降水量预测结果

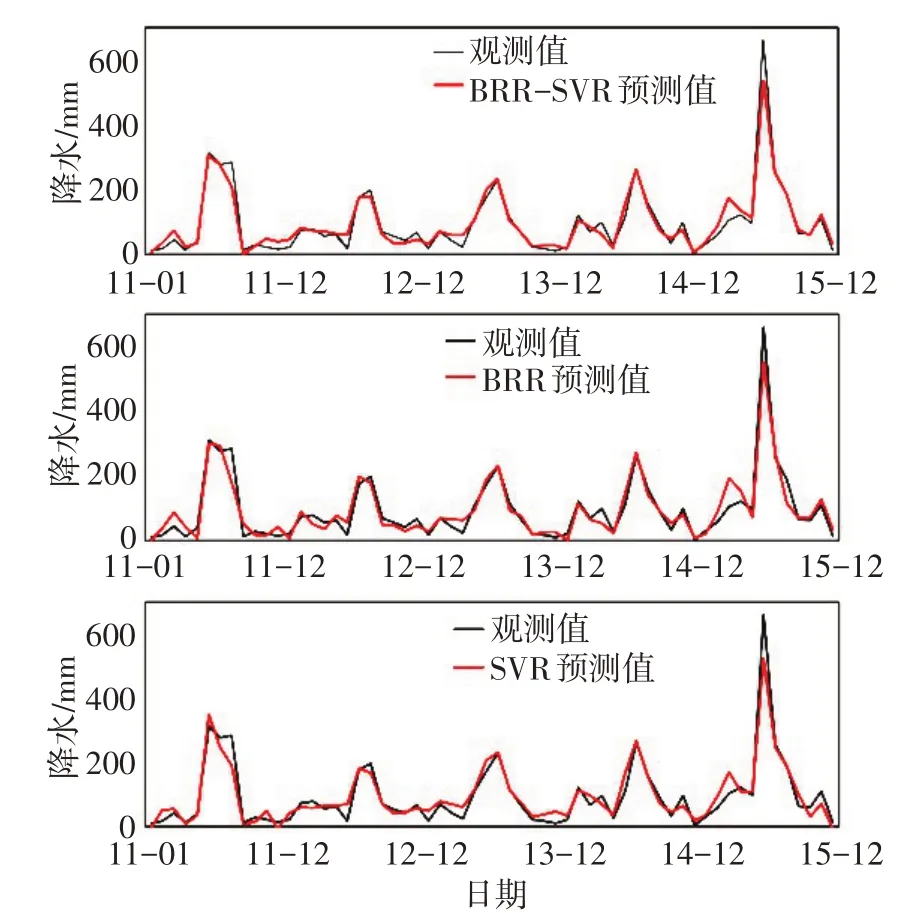
图3 BRR-SVR、BRR和SVR对南京站月降水量预测结果

4.3 讨论本节以各模型对南京站的预测相对误差分布（图5）为例，探讨BRR-SVR模型的精度高于BRR和SVR的原因，与yi分别表示各样本的预测值与观测值。由图5可见，BRR-SVR的误差整体处于较低水平，其在某一点的误差值低于SVR和BRR或更接近两者中的较低值。如2011年9月，BRR的误差接近3，远高于SVR，而BRR-SVR模型的误差更接近SVR；2014年12月，SVR的误差高于4，BRR的误差也接近1，而BRR-SVR模型的相对误差几乎为0，2011年4月、2013年1月和12月都有类似情况，这说明BRR-SVR模型能够对两类模型“取长补短”，使模型的预测误差整体上维持较低的水平。

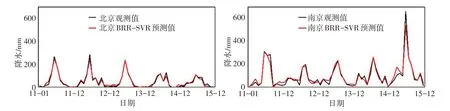
图4 BRR-SVR模型对北京站和南京站预测效果

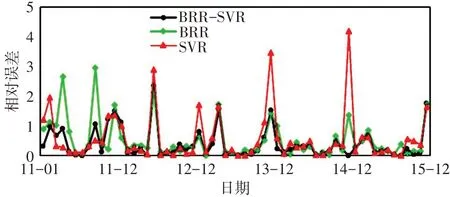
图5 BRR-SVR、BRR和SVR对南京站预测值相对误差

5 结论与展望

本文构建了BRR、SVR和BRR-SVR优化模型，以北京站、南京站和太湖流域7个雨量站的数据来验证模型的性能，结论如下：（1）对文中所应用的各站点，BRR-SVR、BRR和SVR3类模型都存在对汛期降水量的预测效果比非汛期更好的特点；3类模型对北京站的预测效果整体上优于对长江中下游雨量站的预测效果。（2）对于北京站，训练阶段BRR-SVR为最优模型，测试阶段BRR-SVR的精度与SVR基本相同，未体现明显优越性；SVR的精度在训练阶段和测试阶段均高于BRR。（3）对于长江中下游雨量站，BRR-SVR在训练阶段和测试阶段均为最优模型；BRR对训练数据的拟合能力稍逊于SVR，但对新数据的泛化能力强于SVR。

整体上看，对于长江中下游雨量站，BRR-SVR能够从BRR和SVR中选择最优模型，提升预测精度；对于北京站，由于SVR和BRR的精度已经很高，故预测北京站降水使用单一SVR模型即可。本文依据经验选取Daubechies 小波为小波基，以后研究中将尝试用其他类型小波。另外，对北京站的研究，若要得到更具代表性的结论，需要在以后的工作中获取更多站点的降水数据来验证。