贝叶斯概率水文预报研究进展与展望

刘章君，郭生练，许新发，成静清，钟逸轩，巴欢欢

（1.江西省水利科学研究院，江西 南昌 330029；2.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072）

1 研究背景

随着流域产汇流理论研究的深入、计算机技术的迅速发展和预报实践经验的增加，水文预报在理论和实践上都取得了长足发展[1-2]。目前广泛使用的水文预报模型或方案大多是确定性的，即以一个确定的点估计值形式输出给用户[3-4]。实际上，水文预报模型不可避免地存在着输入、结构和参数等诸多不确定性因素影响，进而使得预报结果也具有不确定性[5-6]，即确定性预报值不可能与观测流量值完全吻合，总会出现预报偏大或偏小的误差。以概率分布的形式定量描述和估计水文预报不确定性，不仅可以发布概率预报的中值或均值作为确定性预报，还能给出预报置信区间。概率预报在理论上比确定性预报更加科学准确[7-8]。

传统的确定性水文预报由于没有考虑预报的不确定性，难以对决策风险做出正确评判。比如1997年美国国家气象局发布的北达科他州Grand Forks市雷德河一次洪水位预报值为49英尺，当地官员和居民以为这一预报值是完美（准确无误）的并按此进行防汛准备工作，后来实际水位却高达54英尺，导致发生洪水漫堤，造成重大人员伤亡和财产损失。事后该市参议员Glassheim 说：“如果有人告诉我们这个预报值是不确定的，我们可能会做更加充分的准备”[9]。在实践应用中，概率水文预报能帮助决策者定量考虑风险信息，实现水文预报与决策过程的有机结合，更好地体现水文预报的作用与价值[10-12]。水利部水文水资源监测预报中心提出的新形势下水文情报预报工作的五大转型，明确指出要由确定性预报转向集合预报和概率预报[13]。因此，量化和降低水文预报的不确定性，实现概率水文预报，具有重要的理论意义和实践价值[10-11，14]。

概率水文预报的形式多样灵活，既可以单独对模型输入、模型参数和模型结构进行不确定性分析，也可以对以上这几种不确定性进行全要素耦合分析，还可以直接对模型输出进行统计后处理。

近年来，国内外学者开发了许多水文预报不确定性量化方法，主要包括贝叶斯概率水文预报方法[15-18]、误差概率分布法[19-20]、分位数回归法[8，21-22]和广义线性模型[23-24]等。不同水文预报不确定性量化方法比较见表1。

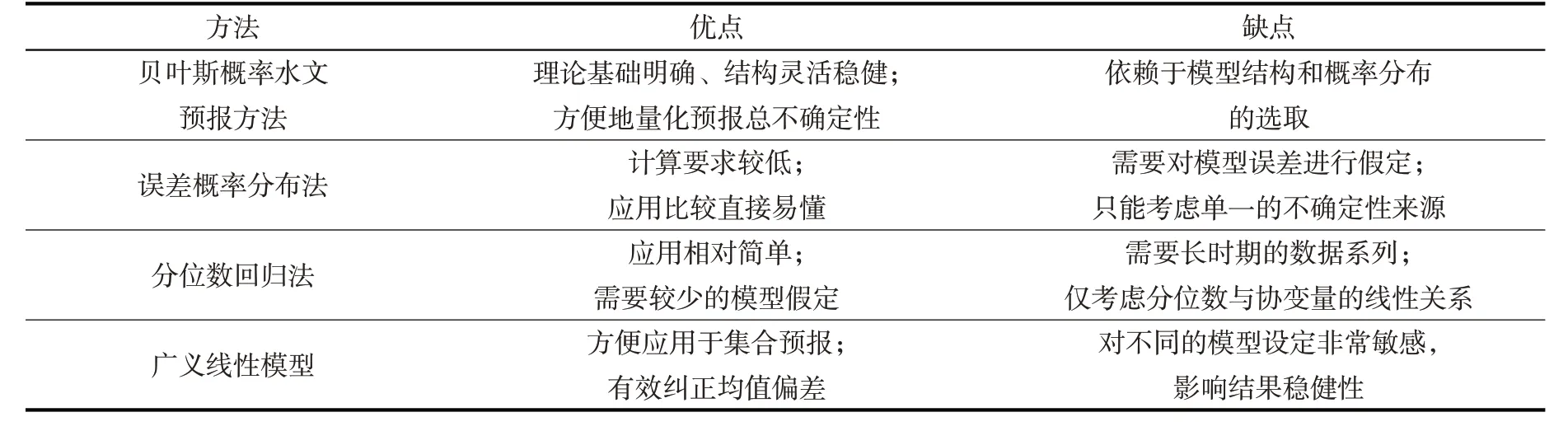
表1 不同水文预报不确定性量化方法比较

在上述这些水文预报不确定性量化方法中，贝叶斯概率水文预报方法理论基础明确，在实际中应用广泛，是目前概率水文预报最具代表性的方法。本文将全面综述贝叶斯概率水文预报的研究进展，并对该领域的未来发展方向进行展望，以期为概率水文预报研究提供技术参考。

2 贝叶斯概率水文预报方法研究现状综述

根据水文预报不确定性来源的不同，从输入资料、模型参数、模型结构和综合不确定性分析等4个方面，综述贝叶斯水文概率预报的研究进展。

2.1 输入不确定性降水是水文模型最重要的输入，直接关系到水文预报结果的好坏。用于水文预报的降水不确定性，可以分为预报时刻已知观测降水（“落地雨”）的不确定性和预见期内降水预报的不确定性。

2.1.1 观测降水不确定性 降水时空分布的随机性与实际情况中固定降水观测站网之间的不符是“落地雨”不确定性的基本来源。Gabellani 等[25]采用随机降雨发生器探讨了降雨时空分布不确定性对典型山区流域洪峰流量预测的影响，揭示了流域降雨不确定性向径流不确定性的传播规律。徐静等[26]分析了降雨的量级、空间分布和时程分配产生的不确定性对流量模拟的影响，表明雨量不确定性的传播对洪水预报的影响处于主导地位，降雨时空分布引起的不确定性对洪水模拟的影响次之。梁忠民等[27]利用抽站法原理推导了以面雨量计算值为条件的面雨量真值的概率分布，从而定量描述流域“落地雨”计算的不确定性。Zeng等[28]以湘江流域及其子流域为例，采用贝叶斯方法分析了雨量站密度和空间分布对新安江模型径流模拟不确定性的影响。温娅惠等[29]研究了降雨量和降雨时间误差对洪水预报精度的影响，表明降雨量误差主要影响洪量和洪峰相对误差，降雨时间误差则主要影响峰现时间误差。

2.1.2 定量降水预报不确定性 除了利用“落地雨”资料外，往往还需要把定量降水预报结果输入到水文模型，延长洪水预见期。目前短期定量降水预报的精度普遍较低，存在较大的不确定性。降水集合预报或降水概率预报技术是刻画和处理定量降水预报不确定性的主要手段，有关这方面基础理论和应用研究可参见文献[30]。包红军等[31]分别以地面雨量站网观测降水和TIGGE集合预报降水输入淮河流域洪水预报模型，比较论证集合概率预报的优势。彭勇等[32]探讨了欧洲天气预报中心（ECMWF）降雨集合预报在桓仁水库径流概率预报的应用。杨明祥等[33]定量分析了样本数量与集合预报技巧的关系，依据ETS评价结果实现了青狮潭水库降水集合预报，经验证构建的集合预报方案较集合算数平均预报技巧更高。

在实际应用中基于集合模式得到的原始降水集合预报结果，常表现出系统性偏差以及欠离散或过离散的情况，需要进行偏差校正以改善预报性能[34]。目前降水集合预报产品的偏差校正方法主要有模式输出统计（EMOS）、人工神经网络方法和贝叶斯模型平均方法（BMA）。其中，BMA方法应用到降水集合预报中，不但能达到偏差校正的目的，而且可以通过对多个预报成员信息进行概率集成提取更为有用的预报信息，具有先进性和广泛的应用前景。Liu等[35]利用BMA方法建立了淮河流域概率定量降水预报模型，研究表明BMA 校正后的降水概率预报结果优于原始降水集合预报。Zhong 等[36]基于TIGGE多中心超级降水集合预报数据，并采用BMA方法进行偏差订正，实现了丹江口水库入库流量的概率预报。此外，降水的时空相关性结构对于水文预报非常重要。由于偏差校正和概率集成方法通常应用在单个雨量站点，同时针对不同预见期也做单独处理，导致降水预报结果的空间相关性和时间连续性丢失。通常采用Schaake Shuffle 方法和ECC（Ensemble Copula Coupling）方法，通过对降水预报集合成员进行重新排序，重建各雨量站点降水预报的空间相关性和时间连续性[37-38]。

2.2 水文模型参数不确定性对于给定的模型结构，其模型参数虽然具有一定的物理意义，但也存在概化的成分，往往只能通过实测资料优选得到。传统的水文模型参数率定基于指定的某种目标函数，依据实测的输入输出资料，采用一定的优化方法得到一套“最佳”模型参数，作为对参数客观真值的估计。国内外学者对各类模型参数的率定和优选问题进行了广泛而深入地研究[39]。1970年代到1990年代末，主要的研究方向是某种优化算法（如遗传算法、SCE-UA 算法等）在模型参数估计中的使用。2000年之前，参数估计中的优化以单目标优化为主，2000年以后这类研究逐步扩展到多目标优化[40]。

2.2.1 广义似然不确定性估计（GLUE）方法 随着研究的深入，后来人们开始认识到模型参数间可能存在一定的互补性和相关性，两套不同的参数可以使模型的目标函数取得相同或几乎相同的水平，即所谓的“异参同效”，从而使得“最佳”模型参数的选择具有很大的不确定性。Beven等[41]最早对这一问题进行了系统研究，并提出了用于评估模型参数不确定性的GLUE 方法。GLUE 方法虽然原理简单，但其自身理论也存在缺陷，越来越多的水文学者对GLUE方法提出了质疑和改进[42-44]。更重要的是，如Mantovan 等[45]所指出的，由于GLUE 方法采用的广义似然函数不具备严格的概率分布形式，导致推求的参数后验概率分布不具有显著的统计特征，在贝叶斯推理方面的不一致性和不连贯性，因此是一种“伪贝叶斯”方法。

2.2.2 基于贝叶斯理论的MCMC 方法 基于贝叶斯理论的MCMC 方法作为一种正式的贝叶斯方法，在水文模型参数不确定性分析中应用广泛。Bate等[46]采用基于Metropolis-Hastings 抽样算法的贝叶斯MCMC方法，估计概念性降雨径流模型参数。Marshall等[47]从简单、易用，探索参数空间的统计效率和运行速度等方面，比较了4个MCMC算法在概念性降雨径流模型不确定性分析中的应用效果，发现自适应Metropolis 算法在很多方面都具有优越性。程春田等[48]发展了一种基于并行自适应Metropolis算法的贝叶斯MCMC方法，用来估计新安江模型参数的不确定性。梁忠民等[49]应用Monte Carlo 途径确定TOPMODEL模型的敏感参数，采用贝叶斯理论和MCMC抽样技术估计敏感参数的后验概率密度分布，探讨了流域水文模型参数及预报不确定性问题。Cheng等[50]在贝叶斯MCMC方法的框架下，比较和改进了用于模型参数不确定性评估的似然函数形式。Zhang等[51]提出了一种基于贝叶斯MCMC的多层因子分析方法，不仅可以用来评价模型参数的不确定性，而且可以估计多个参数的交互作用及其对模型输出结果的影响。Wang 等[52]利用基于Metropolis-Hastings 抽样算法的贝叶斯MCMC 方法进行参数估计及不确定性量化，并与传统的最大似然估计方法（MLE）进行了比较。

2.2.3 GLUE和贝叶斯MCMC方法的比较研究 对GLUE和贝叶斯MCMC这两种模型参数不确定性方法进行比较也是研究的热点。Jin等[53]比较了GLUE方法和正式的贝叶斯方法在计算效率和结果上的差异。结果表明，贝叶斯方法生成的参数后验分布要比GLUE方法稍微更加集中，若GLUE方法使用较高的效率系数阈值（如大于0.8）则与贝叶斯方法得到的结果非常相似。Li等[54]对GLUE方法和贝叶斯MCMC方法在TOPMODEL模型参数不确定性分析中的应用效果进行了比较研究，发现GLUE 方法在取效率系数阈值0.7的条件下得到的预报区间较贝叶斯方法略窄。

2.3 水文模型结构不确定性模型结构是水文模型的核心，是建模者基于水文现象的知识与经验，对水文过程的数学描述。但由于真实的水文现象十分复杂，人们目前还不能完全准确地理解径流形成的每一个物理过程，只能用相对简单的数学公式进行概化，因此往往会出现失真，从而造成水文模型结构的不确定性[55]。考虑到单个水文模型结构的不确定性，很多水文组合预报的方法也得到了水文学者的广泛关注。水文组合预报的优点在于可以集合几个水文模型，吸收几个模型在径流模拟中的优势，规避其短处。

贝叶斯模型平均方法（BMA）在多模型组合预报和模型结构不确定性分析中得到了广泛的应用。BMA与其它多模型综合方法一样，是各个模型预报结果的加权平均，但不同于它们的是，BMA方法还能计算模型间和模型内的误差。Ajami 等[56]将BMA 方法应用于水文模型结构不确定性分析之中，利用BMA对美国的3个盆地流域进行研究，结果表明BMA加权综合的预报值比3个模型单独的预报值精度高。Duan等[57]从多个具有竞争性的水文模型预报结果中，利用BMA方法来获取预报技巧更高和更可靠的概率水文预报，并且发现BMA预报采用多组权重通常比那些仅使用一组权重的预报结果要好。董磊华等[58]利用BMA方法对新安江、SIMHYD和SMAR等3个模型的预报值的后验分布进行综合，以此推断预报量的更可靠概率分布。Parrish等[59]提出了一种耦合BMA和数据同化的方法以降低水文模型模拟预报的不确定性。Liang等[60]通过亚高斯模型对原始数据进行转化，根据BMA方法实现了不同水文模型预报结果的综合，从而得到预报变量的概率密度函数及概率预报，并分别在浙江省密赛流域和黄河东湾流域进行了验证。为了克服BMA方法需要假定流量服从某些特定分布（如正态、Gamma）或者数据转化的不足，Madadgar 等[61]提出了耦合Copula 函数的BMA 方法，并发现相较于BMA 方法效果得到改善。Arsenault 等[62]系统比较了包括简单算术平均、基于AIC 信息准则的平均、Bates-Granger 平均、基于SCE-UA 算法优化的平均和BMA 方法在内的9 种模型平均方法在径流组合预报中的应用。He等[63]通过耦合基于Copula函数的贝叶斯处理器和BMA，提出了一种对多个集总式水文模型进行概率集成的新方法（CBP-BMA），使得BMA建模中条件概率密度的限制更小。Huo等[64]提出了一种具有物理基础的BMA方法——Green-Ampt-BMA方法（G-BMA），并证明在半湿润地区GBMA方法在降低洪峰误差和预测不确定性方面比传统BMA方法具有更好的性能。

2.4 综合不确定性水文模型输入、模型参数和模型结构三者的不确定性往往是相互交织在一起的，共同决定了最终预报结果的不确定性大小。这里所指的水文预报综合不确定性分析是指同时对模型输入、模型参数和模型结构3种不确定来源中至少两者进行不确定性分析，通常包括以下3种情形[65-67]：（1）假设模型结构是确定的，同时考虑输入和模型参数的不确定性；（2）假设输入是确定的，同时考虑模型参数和模型结构的不确定性；（3）同时考虑输入、模型参数和模型结构的不确定性。很多学者讨论和强调了研究这种综合不确定性的重要性，因为这种综合不确定性是决策者更加关心的，它在实际决策中更有价值。在综合不确定性分析方面的主要成果有Krzysztofowicz[15]建立的贝叶斯预报系统BFS、Kavetski等[16]提出的贝叶斯总误差分析方法BATEA和Ajami等[17]发展的综合贝叶斯不确定性估计方法IBUNE，其中BFS最具代表性。

2.4.1 BFS 基本原理与发展脉络 美国弗吉尼亚大学Krzysztofowicz 教授是研究在考虑综合不确定性的基础上构建贝叶斯概率水文预报的先驱，他及其团队在这方面做了大量开拓性的研究和探索工作，主要包括解析-数值型BFS、基于变量状态转移的第二代BFS和贝叶斯极值概率预报方法三大部分。

Krzysztofowicz[15]系统地阐述和介绍了解析-数值型BFS，图1显示了其基本结构框架。BFS在算法上分别利用降水不确定性处理器（Precipitation Uncertainty Processor，PUP）[68]和水文不确定性处理器（Hydrologic Uncertainty Processor，HUP）[65]独立估计定量降水预报不确定性和水文不确定性，再通过贝叶斯全概率公式将这两种不确定性进行综合，最后根据得到的后验概率密度和分布函数提供水文要素的概率预报。Herr和Krzysztofowicz[69]进一步将解析-数值型BFS推广至可以考虑降水集合预报的情形。

基于变量状态转移的第二代BFS的最大特点在于它以单步转移概率密度为工具，可以考虑不同预见期流量之间的内在相关性结构。Krzysztofowicz 等[70]融合降水预报不确定性处理器PUP和多变量水文不确定性处理器（multivariate HUP，MHUP）[71]发展了第二版本的解析-数值型BFS用于概率转移预报。Krzysztofowicz[72]利用基于概率转移预报的第二个版本BFS输出产品，给出了极值变量精确的概率分布函数，创建了贝叶斯极值概率预报（BEPF）方法。BFS的发展脉络如图2所示。

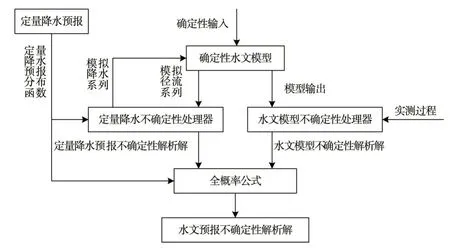
图1 BFS的基本结构框架

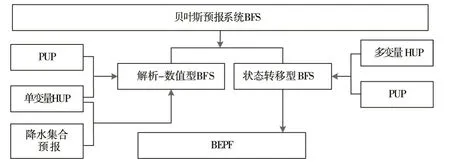
图2 BFS的发展脉络

由于水文预报不确定性来源十分复杂，涉及内容较多，且往往受定量降水预报不确定性的支配，因此对每一个不确定性都进行明确的量化处理是不可行的，也是没有必要的。水文预报不确定性分析要在理论性与实用性之间选择一个折衷的方案，既要尽量精确的考虑到各种不确定性因素，充分利用所有的信息，又要考虑到模型的实用性与可推广性。BFS突破了常规确定性水文模型在信息利用方面的局限性，将水文预报不确定性分为定量降水预报不确定性和水文不确定性两个独立分量，分别对其量化，再通过全概率公式耦合得到综合的水文预报不确定性。由于BFS具有理论基础明确、结构灵活等特点，在理论和实践中得到了迅速的发展和广泛的应用，已经成为目前水文不确定研究的主要手段[5]。BFS不对水文模型附加任何假定与改进，可与任意的水文模型结合，为开发研究概率水文预报提供了一个理论性的框架，引起了国内外水文界的广泛兴趣和关注。但BFS仅仅是给出了研究水文预报不确定性的理论框架，如何提高定量降水预报的精度、如何选取适合的先验分布与似然函数、如何融合多模型预报信息以有效量化和降低水文预报确定性，这些关键问题还有待根据实际情况进一步深入探讨。

2.4.2 国内外学者关于BFS的研究及应用进展 国内外很多水文学者应用Krzysztofowicz 提出的贝叶斯概率预报理论与方法进行各种概率水文预报，并做了一些改进，取得了一系列有益成果。李向阳等[73]利用BP人工神经网络来表达先验分布和似然函数以改进原始的HUP，并基于贝叶斯MCMC方法推求出预报期望值和方差，实现了湖南省双牌水库入库流量的概率预报。邢贞相等[74]在此基础上采用自适应的MCMC抽样算法替代原有的MCMC 方法，在长江支流沿渡河流域应用的结果发现提高了计算效率。Todini[18]在HUP的基础上提出了可以考虑多个确定性预报值进行贝叶斯概率预报的模型条件处理器（Model Conditional Processor，MCP）。张铭等[75]将BFS应用到中长期水文预报中，通过气象因子灰关联预报模型进行中长期降水概率预报，耦合得到丰满水库中长期径流概率预报。Biondi等[76]将依赖于预报降水的HUP 在意大利南部的小流域进行了应用和检验，取得了不错的效果。Bogne等[77]先采用3种实时误差修正方法对确定性水文模型的输出进行校正，在耦合HUP进行概率预报，提高了概率预报的可靠性和精度。Coccia 等[78]回顾了基于模型条件处理器MCP的预报不确定性评价的研究进展，并将MCP拓展为采用2个联合截断正态分布构建实测和预报流量的联合分布，以提高对低流量和高流量的适用性。Todini[79]从理论结构和意大利波河的数值实例两方面对比了HUP和MCP的异同点，发现两者是密切相关的，并且MCP的结果略优于HUP。Biondi 等[80]基于预报可靠性、区间分辨率、准确性和连续等级概率评分CRPS 等多项概率预报评价指标全面系统地评估了BFS的性能。Liu等[81]以长江三峡水库为研究实例，利用HUP评估入库流量预报存在的不确定性，并探讨了概率预报结果在水库汛期运行水位动态控制中的应用。鉴于Copula函数理论在构建多变量联合分布和条件分布中的优势，刘章君等[82]采用该函数在原始空间推导了先验分布和似然函数的计算公式，提出了基于Copula函数的HUP（Copula-HUP）。

Liu等[83]研究比较了自回归模型（AR）、递归最小二乘模型（RLS）和HUP在实时洪水预报校正中的应用，发现HUP误差校正能力优于其他两种模型，且能给出流量的不确定性区间估计。Li等[84]通过HUP分析了淮河流域梅山水库入库洪水预报的不确定性，得到了入库流量的概率预报，并以此进行水库调洪演算的风险分析。Li等[85]通过HUP实现湖南省柘溪水库的概率洪水预报，着重研究探讨了采用不同的实测和预报流量边缘分布线型对概率预报结果的影响。Barbetta等[86]将单变量单模型MCP拓展至多变量多模型MCP，可以考虑不同预见期流量之间的相关性，并通过多水文模型组合降低预报不确定性。Biondi等[87]通过改进现有的BMA和MCP等不确定性后处理器，可以对水文集合预报结果进行概率后处理，得到预报流量的完全概率预报，得到的概率预报更加客观合理。刘章君等[88]提出了基于Copula函数的贝叶斯转移预报（CBTF）方法和基于Copula函数的多变量水文不确定性处理器（CMHUP），进而发展了基于Copula 函数的贝叶斯极值预报（CBEF）方法。巴欢欢等[89]以三峡水库为例，采用TIGGE 降水预报数据考虑降水预报不确定性，结合水文统计后处理开展洪水集合概率预报，并对BMA、Copula-BMA、EMOS和M-BMA等4种后处理方法的有效性进行了分析比较。

3 概率水文预报精度评定和效果检验

水文预报的可靠性如何，精度怎样，是否能满足预期目标，如何进行量化的比较，均需要由评定或者检验给予回答。常用的水文预报精度评定指标主要是针对确定性预报，这些指标不适用于概率预报的精度评定。因此，需要研究提出一套概率水文预报精度评定指标和效果检验方法[90-91]。Gneiting等[92]基于统计学理论指出，概率预报的目的是在保证概率准确性（Calibration）或可靠性（Reliability）的前提下，使得预报分布具有最大的集中度（Sharpness）。从确定性预报、置信区间、概率预报等3个方面介绍概率水文预报精度评定指标和效果检验方法。本文只给出概率水文预报精度评定指标的基本概念，具体计算公式读者可以参阅相关文献。

3.1 确定性预报通常采用概率预报后验均值、后验中位数或后验最可能值作为概率预报的确定性预报结果，其精度评定指标与常用的确定性预报相同。一般采用确定性系数（DC）、径流总量相对误差（RE）、平均绝对误差（MAE）、洪峰相对误差（EQP）和峰现时间误差（TQP）等指标进行精度评价[29，93]。

3.2 置信区间预报置信区间预报评定一般针对于某一指定置信度的预报区间而言，例如90%置信区间。常用的置信区间预报精度评定指标包括覆盖率（CR）、平均带宽（B）与平均相对带宽（RB）、平均偏移幅度（D）等[58，84，90]。覆盖率CR值越接近指定的置信水平越好。对于指定的置信水平，在保证有较高的覆盖率前提下，预报区间平均带宽B或平均相对带宽RB越窄越好。理论上，平均偏移幅度D越小，表示预报区间的对称性越好。

3.3 概率预报通常采用Q-Q图、可靠性（α-index）、分辨率（π-index）和连续概率排位分数（CRPS）等指标来评定概率预报的整体性能[66，94-96]。P值分位数-分位数（Quantile-Quantile，Q-Q）图通过比较预报概率分布与实测值概率分布的差异，从概率角度检验预报概率分布的准确性。Q-Q图曲线越接近于1∶1 线，概率预报结果越合理。α-index 用来定量描述可靠性的高低，而π-index 表示预报概率分布的平均精度。CRPS是结合可靠性和分辨率的综合指标，是目前评估概率预报结果总体效果的常用标准方法，CRPS值越小，表明概率预报性能越好。

4 展望

从上述国内外研究现状可以看出，学者们开展了大量卓有成效的工作，促进了贝叶斯概率水文预报的迅速发展。水文预报中输入（主要是降水）不确定性评估方面，“落地雨”的不确定性一般先获得真实雨量的概率分布，再通过Monte Carlo 抽样方法进行评估，而降水集合预报或降水概率预报技术是刻画和处理定量降水预报不确定性的主要手段。贝叶斯模型平均方法（BMA）在降水集合预报的偏差校正和概率集成方面具有先进性和广泛的应用前景，重建各雨量站点降水预报的空间相关性和时间连续性，最常采用的两种方法是Schaake Shuffle方法和ECC方法。水文预报中水文不确定性评估方面，通用似然不确定性估计方法（GLUE）及其改进方法、基于贝叶斯理论的马尔科夫链蒙特卡洛法（MCMC）是目前应用最广泛的两种水文模型参数不确定性分析方法。水文模型结构的不确定性评估最常用的是贝叶斯模型平均法（BMA）及其改进方法。在综合不确定性分析方面的主要成果有贝叶斯预报系统BFS、贝叶斯总误差分析方法BATEA和综合贝叶斯不确定性估计方法IBUNE。其中BFS理论基础明确、结构灵活，而且实用性强，是目前进行综合不确定性分析的代表性方法。美国弗吉尼亚大学Krzysztofowicz教授及其团队在这方面做了大量开拓性的研究和探索工作，主要包括解析-数值型BFS、基于变量状态转移的第二代BFS和贝叶斯极值概率预报方法。国内外很多水文学者应用Krzysztofowicz提出的贝叶斯概率预报理论与方法开展各种时空尺度、服务于各种目的概率水文预报，并做了一些改进和完善。

由于实际的水文过程非常复杂，水文预报不确定性问题涉及范围相当广泛，解决难度很大，尽管贝叶斯概率水文预报已经取得了很多研究成果，但仍存在不少需要继续深入探讨的问题。综合国内外贝叶斯概率水文预报研究进展，建议进一步深入开展以下几个方向的研究工作：

（1）科学有效地解释、沟通和传播水文预报不确定性信息和概率水文预报产品。实际预报决策中水文预报不确定性是不可避免的，准确描述和量化不确定性本身也是一种重要的决策参考信息。在完善改进模型输入和水文模型、提高确定性预报精度的同时，要科学对待预报不确定性，并自觉利用不确定性信息提升决策水平和效益。如今，确定性预报向概率预报转变是水文预报的发展趋势。很多欧美发达国家已经实现业务化，国内目前处于研究探索阶段，尚未建立概率水文预报业务系统。另外，社会公众和决策者长期习惯使用确定性预报产品和决策思维，如何沟通和传播水文预报不确定性信息并用来决策非常重要，需要预报调度“政产学研用”各界的共同努力。

（2）建立水文集合概率预报框架，估计并降低水文预报的总不确定性。水文预报不确定性来源广泛，需要综合考虑输入、水文模型（包含模型参数和模型结构）等带来的不确定性。目前的水文预报不确定性量化研究很多只单独针对输入不确定性或水文不确定性，同时考虑这两种不同来源的不确定性以量化洪水预报总不确定性的研究相对较少。因此，建立水文集合概率预报框架，估计并降低水文预报的总不确定性，获取水文预报变量的完全概率分布更加客观合理。水文集合概率预报框架通常应包括输入前处理、水文模型预报和输出后处理等模块。输入前处理模块中利用地面站网、天气雷达和卫星遥感等多源降水观测信息进行融合降低“落地雨”不确定性，基于TIGGE多中心超级降水集合预报数据并进行气象预报后处理（即水文预报前处理）量化并降低定量降水预报不确定性。水文模型预报模块采用多个水文模型进行组合预报降低水文模型结构不确定性，并通过输出后处理模块采用的多水文模型输出统计后处理（可隐式地综合考虑水文模型参数和结构不确定性）进一步量化并降低水文模型不确定性。

（3）开展考虑预报变量时空相关性的贝叶斯概率水文预报研究。目前的贝叶斯概率水文预报通常都属于单变量、单站点类型，即只能单独提供某一时刻、某一站点流量的概率预报，没有考虑各预见期流量的时间相关性和各站点间流量的空间相关性，可能造成各时段、各站点流量预报时空相关结构的丢失。因此，贝叶斯概率水文预报的研究发展趋势正逐步从单站点、单变量向多站点、多变量转变，以期准确考虑水文变量间的时空相关性并降低预报不确定性。

（4）深入推动概率水文预报信息在风险决策中的应用。概率水文预报的效果和应用价值最终仍需要体现在决策中，贝叶斯概率水文预报结果只有真正引入洪水预警、水库调度和水资源管理决策中，实现预报与风险决策过程的有机结合，才能更好地体现概率水文预报的价值和效益。然而，目前决策者长期习惯于接受确定性预报产品，因而如何将概率水文预报结果应用于实际决策中依然任重道远，亟需进一步深入研究和探讨。