考虑场次降雨年际变化特征的年径流总量控制率准确核算
杨默远,潘兴瑶,刘洪禄,于 磊,邸苏闯,张宇航
(1.北京市水科学技术研究院 北京市非常规水资源开发利用与节水工程技术研究中心,北京 100048;2.河海大学 水文水资源学院,江苏 南京 210098)
1 研究背景
年径流总量控制率是海绵城市建设的主要建设目标和关键考核指标,与年径流总量控制率相对应的设计降雨量,是海绵城市规划设计的重要依据,也是模拟评估时的重要输入条件[1-4]。因此,年径流总量控制率核算,即获取准确的年径流总量控制率-设计降雨量对应关系,是海绵城市研究中的关键问题[5-8]。在2014年发布的《海绵城市建设技术指南—低影响开发雨水系统构建(试行)》(后文简称《指南》)和2018年发布的《海绵城市建设评价标准》(后文简称《标准》)中,均给出了年径流总量控制率的核算方法,即根据至少30年的日降雨资料,在扣除小于等于2 mm的无效降雨数据后进行排频计算,从而确定年径流总量控制率-设计降雨量对应关系,可以理解为日雨量经验排序的百分位数。
上述方法是目前进行海绵城市试点建设和推广应用时的主要依据,但随着对海绵城市理解的不断加深,以及实际建设经验的不断丰富,年径流总量控制率的内涵以及计算方法引起了相关学者的广泛讨论[9-11]。张建云等[12]认为场次降雨特征(总量和时程分布)对海绵城市的径流控制效果有直接影响,在计算径流控制指标时应考虑区域场次降雨特征;王家彪等[13]对比分析了降雨总量控制和降雨场次控制模式的主要区别和侧重点;李俊奇等[14-16]探析了极端降雨事件对年径流总量控制率的影响规律,给出了极端降雨事件的最佳扣除比例,并对比分析了国内外三种径流总量控制率计算方法;张质明等[17-18]探讨了年径流总量控制率的空间分布规律与气候变化的影响。林炳章等[19]基于大量计算,更明确指出“就全国范围的平均情况,与日雨量经验排序70%对应的设计日雨量仅相当于1年一遇的30%(0.304);而与85%对应的设计日雨量仅相当于1年一遇的50%(0.534)。”
根据年径流总量控制率的概念和内涵,年径流总量控制率计算的核心是对场次降雨事件的排频计算,反映的是场次降雨特性。但《指南》和《标准》中给出的年径流总量控制率计算方法均是基于日降雨数据。因此,利用人为划分的日降雨数据反映实际的场次降雨特性难免会存在一定的偏差,而这一偏差对年径流总量控制率计算结果的影响仍有待更多深入的定量研究。此外,年径流总量控制率计算中,普遍认为历史降雨资料序列越长,资料的代表性就越好,计算得到的年径流总量控制率就越准确。这在一定程度上忽视了长降雨序列特征变化对年径流总量控制率的影响,当历史降雨序列存在突变或趋势性变化时,过长的历史资料意味着更多地受到与现阶段降雨特性不符的“负面”数据影响,从而降低了年径流总量控制率计算结果的准确性。因此,有必要在识别降雨序列特征阶段性变化的基础上,合理选取用于年径流总量控制率计算的代表性历史序列长度。
本文围绕年径流总量控制率核算中有关基础资料选取的2项关键问题开展研究,以北京市长序列场次降雨数据为例,对比分析日降雨序列和场次降雨序列的降雨特性,定量分析场次降雨划分方法对年径流总量控制率的影响。在此基础上,提出场次降雨序列年际变化特征的识别方法,并定量判别场次降雨序列统计特征对年径流总量控制率计算结果的影响。研究成果有助于进一步完善年径流总量控制率精细化核算方法,为年径流总量控制率指标的合理确定和海绵城市建设的科学开展提供参考和帮助。
2 资料和方法
2.1 场次降雨数据场次降雨数据来源于北京市水文部门,雨量站为北京城市副中心海绵城市试点区邻近的通州站,数据资料为场次降雨摘录数据,降雨序列长度达66年(1951—2016年),满足长序列年际变化特征分析的需求。该雨量站与《指南》选用的北京站相距17.5 km,且均位于北京平原区(图1),因此两个站点的降雨资料具有较好的一致性,年降雨序列相关系数为0.87(图2)。

图1 雨量站点空间位置
2.2 场次降雨划分方法对于某一确定的历史降雨序列,不同的降雨场次划分方法,将得到不同的场次降雨特征识别结果。目前在海绵城市建设中常用的降雨场次划分方法主要有两种:(1)《指南》和《标准》中采用的日降水数据,例如前后两日20时至20时内的累计降雨量;(2)按照实际降雨过程进行划分,其关键是最小降雨间隔时间(T)的合理确定。场次降雨数据一般以最小降雨间隔时间为判别标准进行划分,能够较为客观地反映实际降雨过程。而日降雨数据是在人为给定每一日起止时间(如0点、早8点或晚8点等)的基础上,通过统计在某一日内的降雨总量得到的。在特定情况下(图3中降雨事件1),日降雨数据和场次降雨数据保持一致,但对于大多数情况,日降雨数据可能导致人为整合日内多场小降雨事件(图3中降雨事件2和降雨事件3)或分割一场连续降雨事件(图3中降雨事件4),进而造成较大的偏差。因此,在数据资料的时间分辨率满足条件时(至少为小时降雨数据),按照最小降雨间隔时间进行降雨场次划分更为合理。在本文研究分析中,综合考虑降雨特性(普遍为6 h内的短历时降雨)、排水设施排空时间(6~12 h)和流域退水时间(3~6 h)等因素,将最小降雨间隔时间确定为6 h[20-24]。

图3 场次降雨和日降雨数据对比
2.3 年径流总量控制率计算方法本文的年径流总量控制率核算参考《指南》和《标准》中给出的方法,具体如下:选取不同资料长度(不局限于至少30年这一标准)的日降雨或场次降雨数据,扣除小于等于2 mm(不产生径流)的降雨事件,按照降雨量由小到大进行排序,统计小于某一降雨量(设计降雨量)的降雨总量(小于设计降雨量的降雨事件按实际降雨量计算降雨总量,大于设计降雨量的降雨事件按设计降雨量计算出降雨总量,两者累积求和)在总降雨量中的比例,此比例即为该设计降雨量对应的年径流总量控制率。
2.4 突变及趋势检验M-K突变和趋势检验是一种非参数检验方法,其优点是不需要样本遵循一定的分布,同时不受少数异常值的干扰,因此适用于水文变量的分析[25-28]。通过分析UFk和UBk′这两个统计量可以识别时间序列的趋势和突变点。若UFk>0,则序列呈上升趋势;UFk<0,则表示呈下降趋势。如果UFk和UBk′这两条曲线存在交点,且交点位于临界区间内,则交点对应的时刻即是突变发生的时刻。
3 降雨场次划分方法对年径流总量控制率的影响分析
3.1 场次降雨数据和日降雨数据对比分析基于1951—2016年北京市场次降雨数据,按照最小降雨间隔时间为6 h进行划分,得到降雨事件共3530场,其中有效降雨(降雨量>2 mm)共计2109场。基于日降雨数据统计得到的降雨事件共4577场,其中有效降雨2525场。从不同量级的场次降雨事件数量统计结果可以看出(图4),日降雨数据统计得到的小量级降雨事件(降雨量在2~25 mm范围内)明显多于场次降雨数据。对于2~5 mm的降雨事件,日降雨数据统计得到820场,而场次降雨数据统计得到602场,偏多36%。对于中等量级降雨事件(场次降雨量在25~30 mm范围内)而言,日降雨数据统计得到的场次数低于场次降雨数据统计得到的场次数(偏低17%),此量级降雨场次也是海绵城市建设的重点控制对象[29]。
如前文所述,较实际场次降雨过程而言,日降雨数据一方面会合并多场小量级降雨事件(减少小量级降雨事件发生频率),另一方面会分割降雨事件(增加小量级降雨事件发生频率),两方面作用是相互影响的。具体对于北京市场次降雨数据而言,日降雨数据对降雨事件的分割作用占主导,造成中等量级降雨事件的减少和小量级降雨事件的增加,进而可能会高估年径流总量控制率计算结果。

图4 场次降雨量分布特征
3.2 基于场次降雨数据的年径流总量控制率计算根据《指南》中给出的资料长度取值标准,结合研究区数据资料基础,共考虑1987—2016年(30年)和1951—2016年(66年)两种降雨序列长度,分别计算基于日降雨数据和场次降雨数据对应的年径流总量控制率-设计降雨量关系(图5和表1)。计算结果表明,1987—2016年日数据计算结果与《指南》中给出的数值具有较好的一致性,整体偏差在1%左右。在相同资料长度条件下,较场次降雨数据而言,日降雨数据计算得到的设计降雨量明显低估,对于1987—2016年序列计算结果,整体低估约14%,对于1951—2016年序列计算结果,整体低估约19%。具体而言,在海绵城市实践中重点关注的85%年径流总量控制率条件下,30年序列日降雨数据计算得到的设计降雨量较场次降雨数据计算结果而言偏低5.9 mm。在具体的海绵规划设计中,设计降雨量偏低5.9 mm意味着海绵设施规模的严重不足,进而会影响到真实年径流总量控制率指标的完成。
较1987—2016年降雨序列而言,1951—2016年降雨序列计算得到的设计降雨量偏高约20%,这一现象反映出研究区不同阶段的场次降雨特性差异明显,选取近30年降雨(1987—2016年)资料仅能够反映现阶段的年径流总量控制率-设计降雨量关系,而对长序列历史降雨过程的周期性和趋势性变化特征考虑不足。因此,有必要在进一步识别研究区场次降雨序列年际变化特征的基础上,充分利用整个历史降雨序列资料(1951—2016年),综合确定年径流总量控制率-设计降雨量关系。

表1 日数据和场次数据设计降雨量计算结果 (单位:mm)

图5 年径流总量控制率-设计降雨量对应关系
4 场次降雨年际变化特征及其对年径流总量控制率的影响分析
4.1 场次降雨序列年际变化特征识别在场次降雨数据年际变化特征分析中,选取了6个场次降雨特征值,并分别进行M-K突变和趋势检验,根据各场次降雨特征值检验结果,综合判定场次降雨的年际变化特征。6个场次降雨特征值分别为:年降雨总量、年降雨场次数、年平均场次降雨历时、年平均场次降雨量、年平均降雨间隔时间和年最大场次降雨量。

图6 场次降雨特征值的M-K突变检验结果
通过M-K 突变检验(图6),识别得到北京市海绵城市试点区场次降雨过程主要存在两个突变点:第一个突变发生在1964年,年降雨总量、年平均场次降雨量和年最大场次降雨量序列均在该处发生突变;第二个突变发生在1996年,年平均场次降雨历时和年平均降雨间隔时间序列在该点发生突变。因此,整个降雨过程可划分为3 个阶段,分别为:1951—1964年、1965—1996年和1997—2016年。通过计算UFk统计量,可以判定各特征值序列的变化趋势,其计算结果如表2所示,仅降雨总量序列在阶段Ⅲ表现为显著上升的趋势,其他特征值在各阶段均无显著性变化趋势,因此,研究区降雨序列发生的两次突变为均值突变。
整体而言,降雨序列的平均场次降雨历时、平均场次降雨量和最大场次降雨量呈显著下降趋势,反映出降雨事件的量级呈显著降低趋势。3个阶段的场次降雨特性区别明显,较阶段Ⅰ而言,阶段Ⅱ的年降雨总量、年平均场次降雨历时、年平均场次降雨量、年平均降雨间隔时间和年最大场次降雨量分别下降约17%、36%、23%、12%和39%,下降趋势明显;而阶段Ⅲ与阶段Ⅱ相比,年降雨总量下降约10%,年平均场次降雨历时下降约19%,年平均场次降雨量下降约11%,下降趋势有所缓解。

表2 场次降雨特征值的阶段性统计结果
4.2 年径流总量控制率合理区间确定在具备较长的历史降雨资料,且得到降雨序列阶段性变化过程划分结果的基础上,可以通过以下3种方式核算年径流总量控制率-设计降雨量关系:①仅利用现阶段降雨序列(阶段Ⅲ,1997—2016年)进行核算;②利用整个序列(1951—2016年)的降雨资料进行核算;③利用3个阶段(1951—1964年、1965—1996年、1997—2016年)的降雨资料分别进行核算。
方式①能够最为准确地反映目前这一阶段的降雨特征,但对于北京市海绵城市试点区而言,阶段Ⅲ处于一个相对偏干旱的阶段,仅利用阶段Ⅲ的降雨数据不利于应对未来可能发生的降雨非平稳变化情势,可能会在一定程度上造成设计降雨量的低估。方式②利用全部历史降雨资料进行计算,过多地引入了与现阶段降雨特征不符的历史降雨序列,计算得到的年径流总量控制率-设计降雨量关系缺乏对降雨特征变化的响应。方式③针对不同降雨阶段分别进行核算,能够反映可能发生的偏干旱和偏湿润的降雨特征,为年径流总量控制率的估算提供更加全面和客观的变化区间参考(图7)。
对于北京市海绵城市试点区而言,阶段Ⅰ的降雨量级整体偏高,因此在一定的设计降雨量条件下,仅能够实现较低的年径流总量控制率目标;与阶段Ⅰ相反,阶段Ⅲ的降雨量级整体偏低,因此在一定程度上对应较高的年径流总量控制率计算结果;阶段Ⅱ的年径流总量控制率-设计降雨量关系介于阶段Ⅰ和阶段Ⅲ之间。具体而言,考虑不同的场次降雨演变阶段,在设计降雨量等于20、30和50 mm 时,得到的年径流总量控制率合理区间分别为54.1%~69.5%、65.4%~80.5%和77.8%~90.3%。
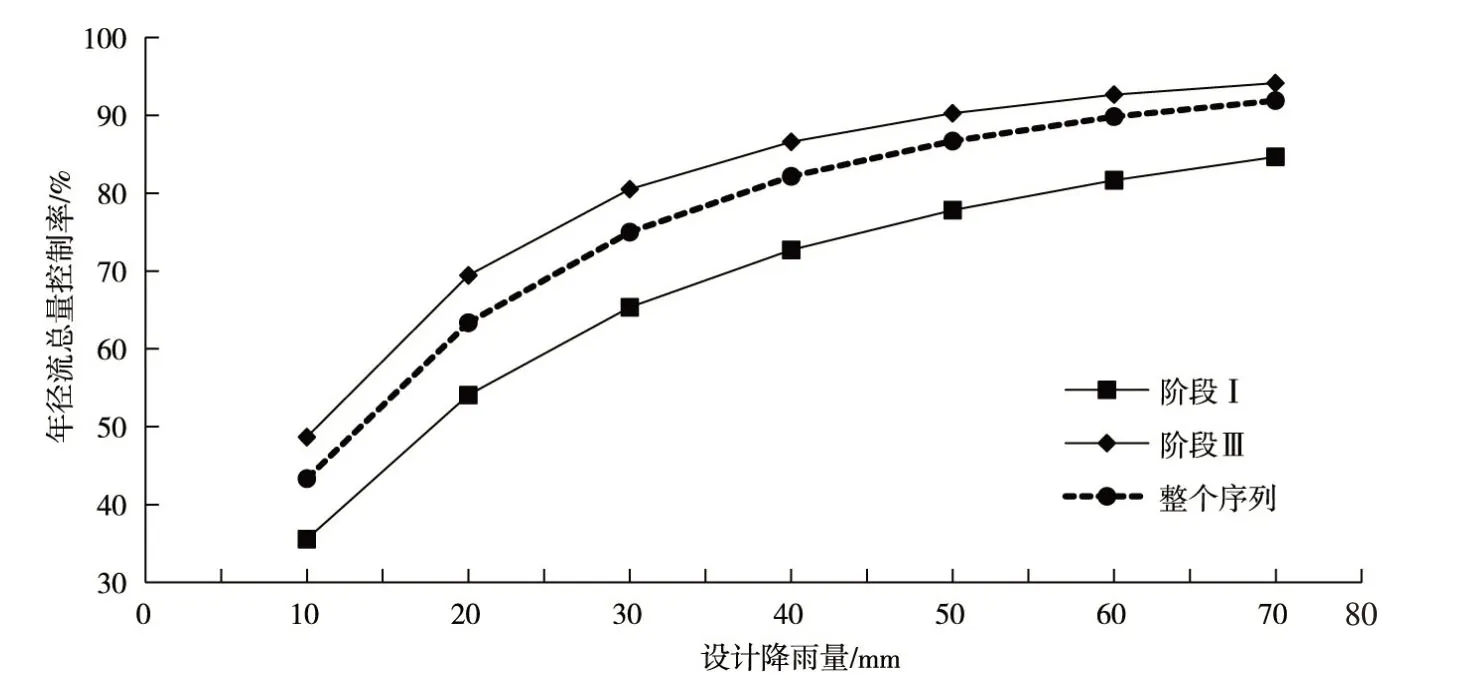
图7 年径流总量控制率-设计降雨对应关系计算结果
5 结论
本文以北京市海绵城市试点区长序列降雨过程为例,围绕年径流总量控制率核算中降雨资料的合理选取这一问题开展研究。首先对比分析了日降雨数据和场次降雨数据反映出的场次降雨特性,并定量分析了场次降雨划分方法对年径流总量控制率计算结果的影响。在此基础上,通过M-K突变和趋势检验,识别了场次降雨序列6个特征值的年际变化并进行了阶段划分,进而计算得到了年径流总量控制率合理取值区间。
通过对近30年的降雨数据分析,发现日降雨数据会增加小量级降雨事件数量,降低中等量级降雨事件发生频率,进而造成设计降雨量整体低估约14%。对应85%年径流总量控制率条件,日降雨计算得到的设计降雨量偏低5.9 mm。在实际的海绵规划设计中,设计降雨量的低估意味着海绵设施规模的不足,进而会影响到海绵城市建设真实年径流总量控制率指标的实现。
场次降雨序列年际变化对年径流总量控制率影响显著,在进行年径流总量控制率计算时,应首先识别场次降雨阶段性变化特征。通过对6个场次降雨特征值进行M-K突变和趋势检验,将降雨序列划分为3 个阶段,分别为:1951—1964年、1965—1996年和1997—2016年,降雨量级依次降低。针对上述3 个降雨阶段分别核算年径流总量控制率-设计降雨量关系,能够反映整个历史降雨序列(1951—2016年)中偏干旱和偏湿润阶段的降雨特征,为年径流总量控制率的估算提供更加全面和客观的变化区间参考。具体而言,在设计降雨量等于20、30和50 mm时,年径流总量控制率合理区间分别为54.1%~69.5%、65.4%~80.5%和77.8%~90.3%。
科学选取降雨资料序列是进行年径流总量控制率统计分析的重要基础。在数据资料基础允许的前提下,应优先利用场次降雨数据进行年径流总量控制率计算,并开展针对性的场次降雨特性年际变化特征分析,确定年径流总量控制率合理变化区间,进而考虑海绵城市建设目标、海绵城市建设生命周期和未来气候变化情景等综合因素,确定最终的年径流总量控制率取值。上述核算方法能够提高年径流总量控制率-设计降雨量对应关系计算结果的科学性,有效指导海绵城市的规划设计,从而确保最优的海绵城市建设效果与合理的工程建设投入。

