排考场次分配方法及其SQL实现
袁子昂
(杭州电子科技大学计算机学院,杭州310018)
0 引言
高校期末排考场次分配,要将上万名学生和数百门课程安排到若干场次,每一场次不能出现课程冲突(同场的任意两门课程不能有相同的学生),也不能超过容量限制(考场数量和容量所限)。现实中总是希望考试场次尽量少,以保证在一周左右完成考试。文献[1]和文献[2]证明了排考时间表是NP难问题,文献[3]和文献[4]提出了用顶点着色算法来解决排考场次分配问题,但未考虑容限。本文用带权顶点着色算法求解容限约束下的场次分配问题,并给出了该算法在SQL Server上的具体实现,对其中的T-SQL脚本进行简单修改就能适应各学校的具体情况。
1 场次分配的带权顶点着色算法
场次分配的输入是选课集SC={(学号,课程号)},用二部图表示如图1。
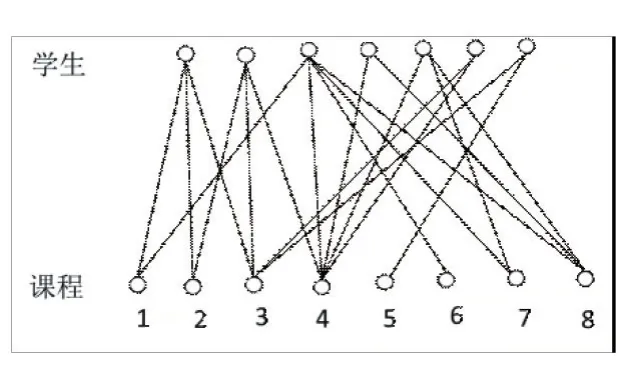
图1 选课集二部图
由选课集可导出带权的课程冲突关系如图2,图2中的含权顶点表示课程,顶点的权表示学生数,顶点间的边表示冲突,顶点的度表示与该课程有冲突的课程总数。
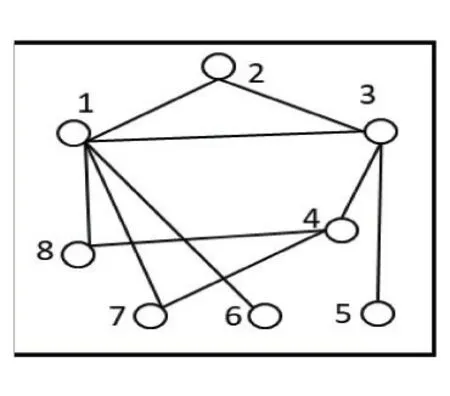
图2 课程冲突关系图
场次分配的输出是场次集CT={(课程号,学生数,场次号)},其中课程号和学生数可由选课集得到,初始时,所有的场次号均为0,表示课程待分配。分配完成后,场次号取值为1,2,…,n,并且满足约束:场次号相同的课程彼此不冲突,同一场次的学生数之和低于限额。
在不考虑容限约束时,场次分配与顶点着色问题等价,可用贪心算法求解:①k=1。②若图中没有无色顶点则结束;否则,从图中找度数最大的顶点,染色为k。③从无色且与k色顶点无连接的顶点中,找与无色顶点连接数最大的顶点,染色为k;重复本步直到没有满足条件的顶点。④从图中删除k色顶点及其关联的边。⑤k=k+1,回第②步。以上步骤如图3a,3b,3c所示,最后结果如图3d,8个顶点被分为3组:第1组(1,4,5),第 2 组(2,6,7,8)和第 3 组(3)。
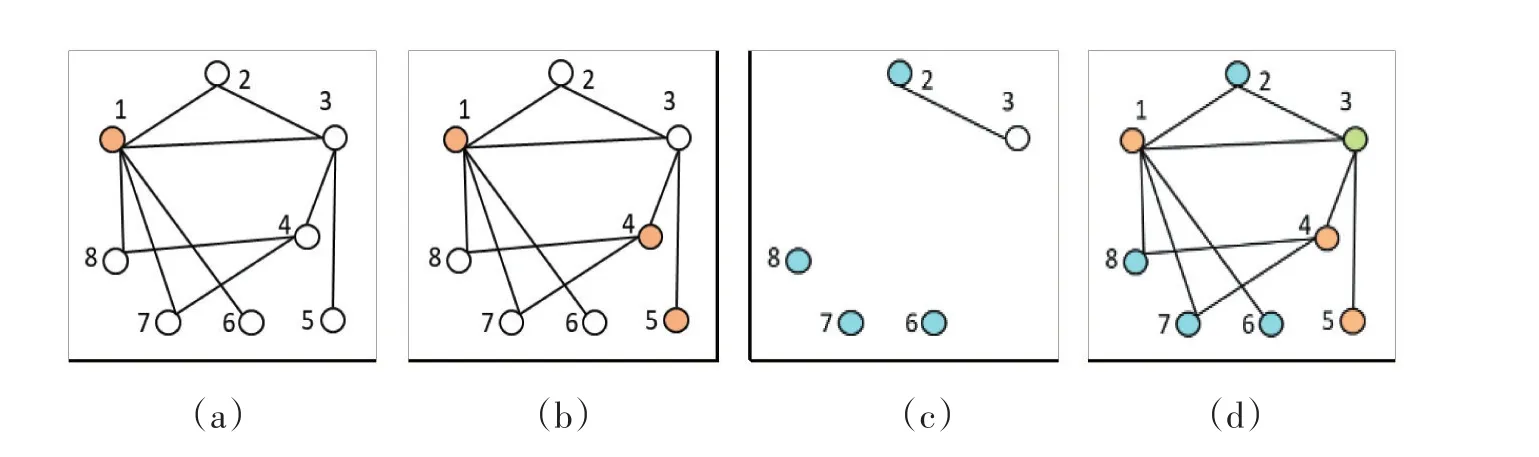
图3 顶点着色贪心算法
考虑容限时,场次分配与带权顶点的着色问题等价,每次对一个新的顶点染色时,要检查改色节点的权重之和是否超过容限。容限记为max,余量记为rest,顶点和权重记为vi和wi,对以上算法进行调整:
带权顶点最小着色算法
(1)k=1。
(2)若图中没有无色顶点则结束;否则,找到度数最大的顶点vi,染色为k,rest=max-wi。
(3)从无色且权值小于rest且与k色顶点无连接的顶点中,找到与无色顶点连接数最大的顶点vi,染色为k,rest=rest-wi,重复本步直到没有满足条件的顶点。
(4)从图中删除k色顶点及其关联的边。
(5)k=k+1,回第(2)步。
2 算法的SQL实现
在SQL Server上,通过设计数据库、预处理、分配、检查结果等四个步骤完成场次分配。
2.1 数据库设计
在SQL Server上创建一个数据库,其中创建三个表:选课表、场次表和冲突表。
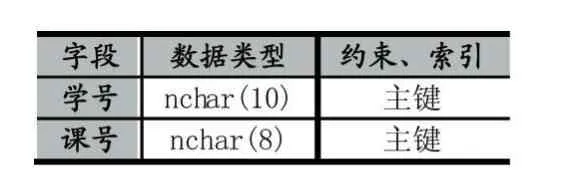
表1 选课表
选课表用于存放选课数据,表中的每一行表示一个学生要参加一门课程的考试。
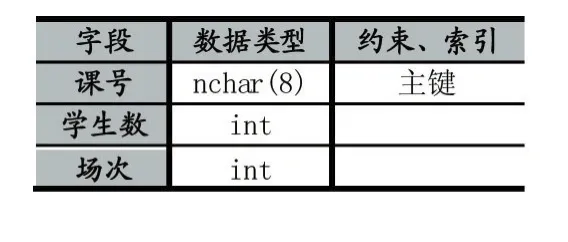
表2 场次表
场次表用于存放场次分配的中间过程和结果,表中的每一行表示一门课程分配进一个场次,若有n门课程,则共有n行。所有的课程的初始场次都为0,表示未分配;在分配过程中,课程的场次将分别变为1,2,…,场次号相同的课程属于同一场次。
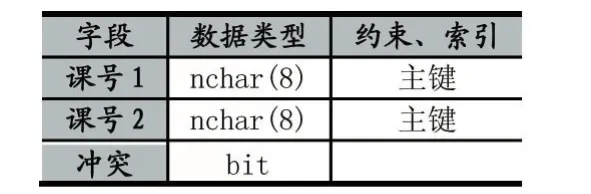
表3 冲突表
冲突表用于存放课程关系,冲突值取1/0表示有/无冲突。为编程方便,一对课程c1和c2会存入两行:(c1,c2,1/0)和(c2,c1,1/0)。冲突表中的初始数据由选课表导出,在分配过程中,数据将逐渐减少直至为空。
2.2 预处理
预处理用于生成选课表数据、场次表初始数据和冲突表初始数据。
选课表数据可从Excel表导入到数据库,也可从现有的信息系统中取得。
场次表初始数据从选课表中取得,所有课程的初始场次都置为0。
生成场次表初始数据的T-SQL脚本:

冲突表初始数据从选课表中取得。首先取得所有的课程对,若有n门课程,则得到n*(n-1)行,所有课程对的冲突都设为0;然后从选课表中找到有冲突的课程对,将其冲突设为1。
生成冲突表初始数据的T_SQL脚本:

由于冲突表在分配过程中数据会逐渐减少,为了对分配后的结果进行检查,对冲突表备份得到备份冲突表。
2.3 场次分配
场次分配用一个存储过程来实现,该存储过程有一个输入参数@max,执行该过程会更新场次表。
创建存储过程的T_SQL脚本:


2.4 检查结果
对得到的场次表进行检查,一是检查是否所有课程都分配了场次,只要场次表中所有行的场次列都不为0,即说明检查通过;二是检查每一场次内有无冲突,只要场次相同的课程冲突值之和为0,即通过检查。三是检查每一场次考生数是否超过容限。
场内冲突检查的SQL脚本:

3 实验
取某校2017学年第一学期的选课数据,含10037名学生,193门课程,36714条选课记录,每一场次的容限为5000人。经过预处理,得到课间冲突关系共2796对,场次分配过程在5秒内执行结束,得到考试场次共20场,分场次的课程数和学生人数如表4。
实验中发现,后分配的课程不能移入先分配的场次,但某些先分配的课程可以移入某些后分配的场次,这一现象是贪心算法造成的。如图3中,被放入第1组的5号节点,也可以放入第2组;而第2组中的6,7,8号节点,可以全部放入第3组。在实际应用中,这一特点为实际排考工作提供了一定的调整余地。
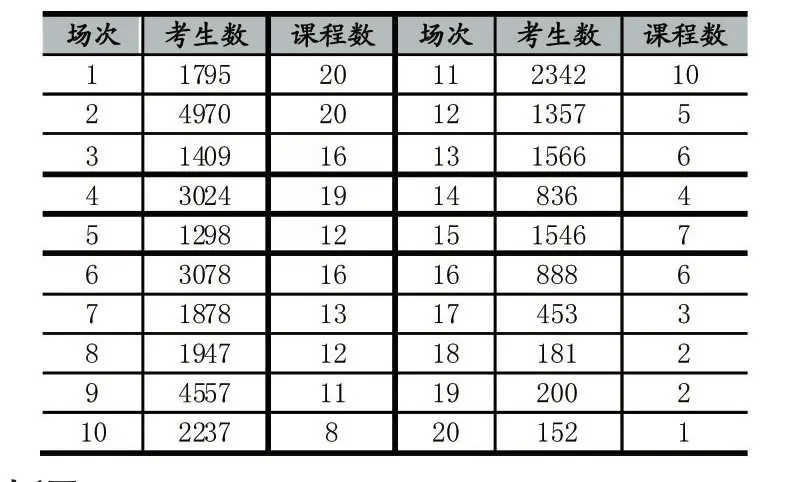
表4 场次考生数量
4 结语
本文将带容限约束的排考场次分配问题转化为带权图顶点最小着色问题来求解,给出了一种贪心算法,并给出了算法在SQL Server平台上的具体实现,解决方案易于部署实现,对本文中的T-SQL脚本进行简单修改就能适应各学校的具体情况。

