张量Z-特征值的新包含域

何 军，刘衍民

(遵义师范学院数学学院，贵州遵义563006)

1 预备知识

张量特征值是矩阵特征值的推广，并广泛应用到医学成像、图像分割和量子计算等问题中[1-7].令（实数集），Qi在文献[1]中给出了如下的张量Z-特征值的定义.

定义1[1]设（阶维），若存在非零向量和数使得

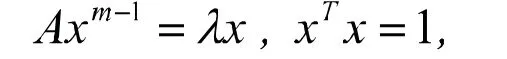
其中，

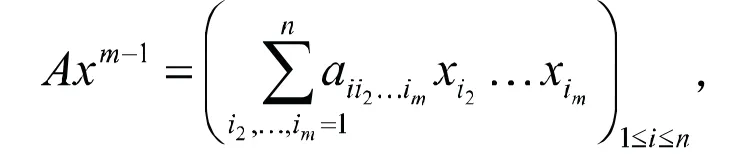
张量Z-特征值在最佳秩一逼近以及高维统计中都有着重要的

引理1[8]设，则

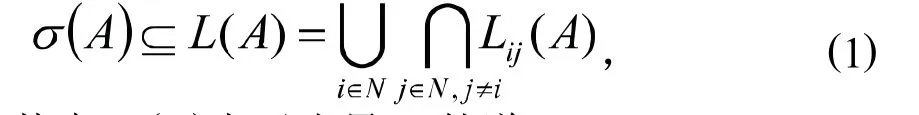
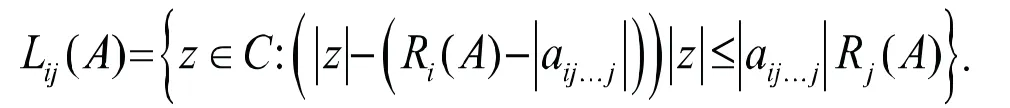
引理2[9]设是非负不可约且弱对称的张量，则(A)是张量的正Z-特征值，并且(A)对应的Z-特征向量是正向量.

基于引理1和引理2，Wang等在文献[8]中给出了如下的非负张量Z-谱半径上界.

引理3[8]设是非负弱对称不可约的张量，则

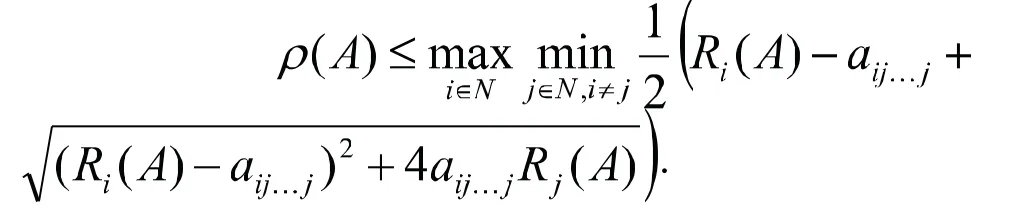
令张量A的阶m≥4，本文给出了张量Z-特征值的新包含域，并通过张量Z-特征值的新包含域，给出了非负张量Z-谱半径的新上界.数值例子说明本文结果优于文献[8]中的结果.

2 主要结果

对任意k∈N，令

我们可得如下张量Z-特征值的新包含域.

其中，

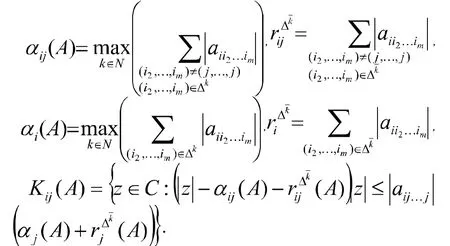
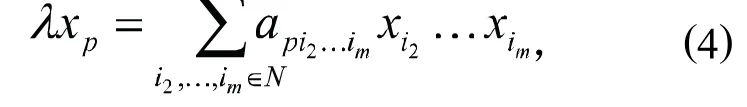
在等式(4)两边同时取绝对值有

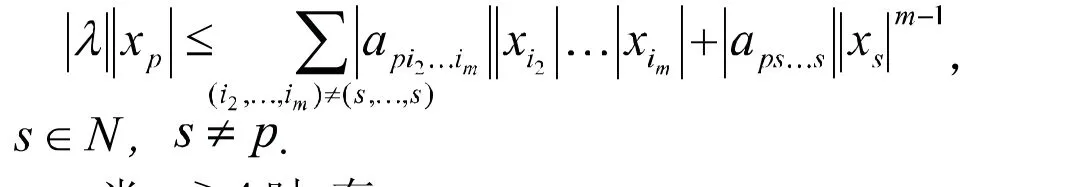
当m≥4时，有

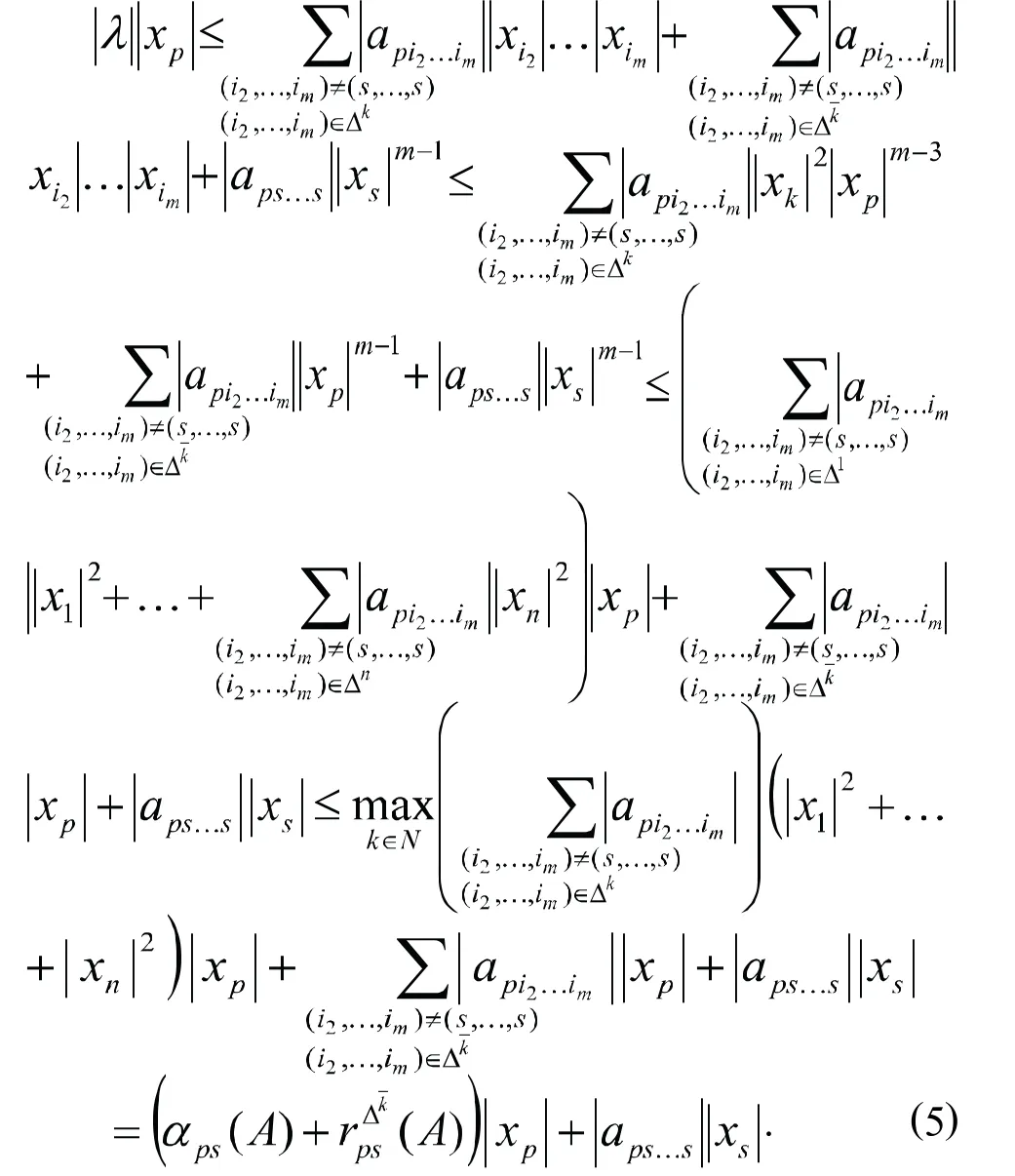
由(5)和(6)可得

证毕

注 由定理1的证明可得，

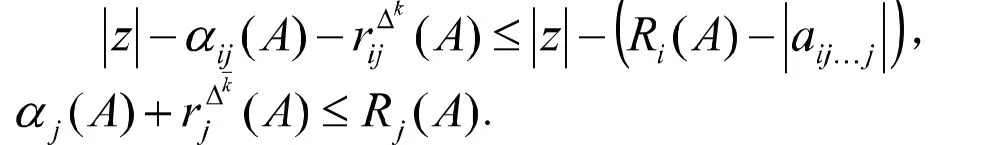
则可得

基于定理1，我们可得如下非负弱对称不可约张量的Z-谱半径的新上界.

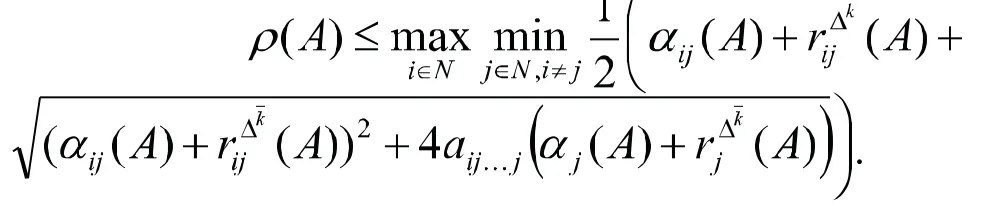
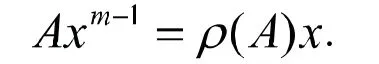
由定理1可知，存在p∈N使得

即

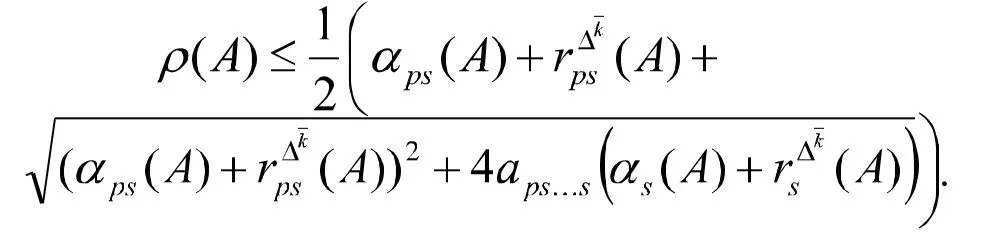
由s的任意性可得

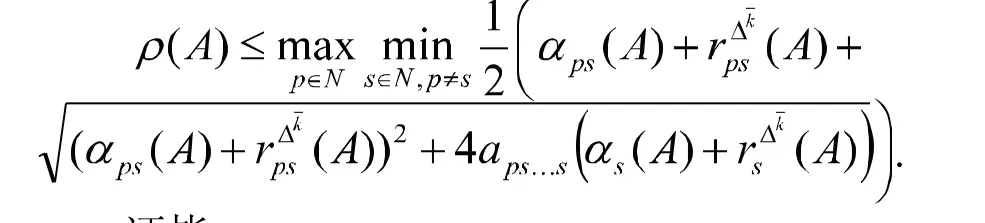
证毕.

3 数值例子

本节我们用数值例子来说明结果的有效性.

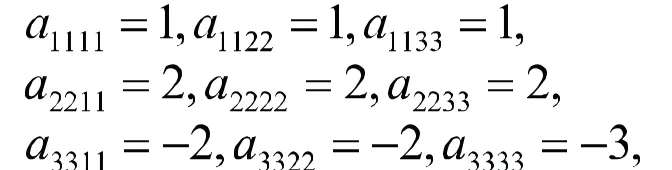
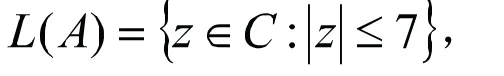
由定理1可得

由图1可以看出，定理1的结果比文献[8]中定理3.2的结果好.

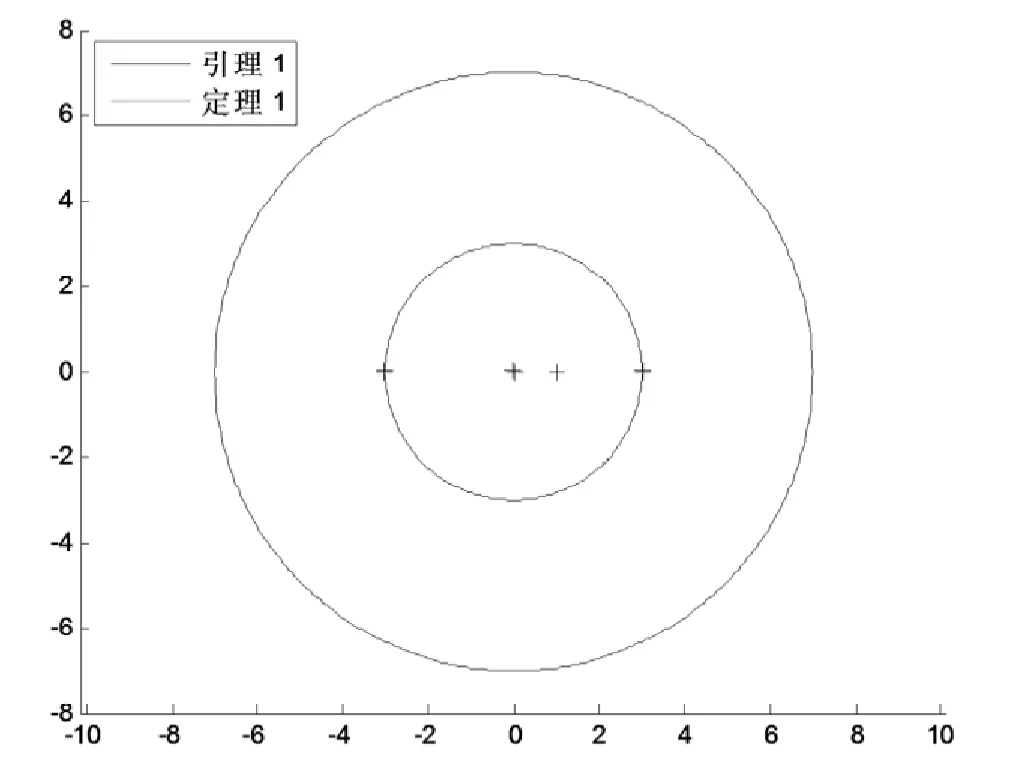
图 1 L（A）VS K（A）

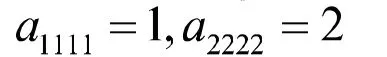
由例2可以看出，定理2的结果比文献[8]中定理4.5的结果好.