一类受媒体影响的传染病模型的动力学分析

姜大要，薛亚奎

（中北大学理学院，太原 030051）

现代社会中，快速发展的大众媒体对人们的生活方式产生了越来越深刻的影响，并且成为人们获取健康信息的重要渠道。在传染病的传播和控制过程中，媒体会报道疾病的传播情况，并告诉人们采取相应的预防措施（如戴口罩、减少去公共场所的次数、经常洗手等）来阻止和减少疾病的传播和发生［1］。

利用数学模型可以分析疾病的传播和控制，以及预测一段时间内疾病是如何传播的［2-5］。在疾病的传播和控制过程中，媒体报道的作用不可忽视。因此，近年来部分学者对此进行了相关的研究。Yorke等［6］通过建立一个性传播的 SIS模型研究媒体报道对疾病传播的控制。文献［7］在信息传播与染病者的死亡人数成正比的假设下，建立了一类带时滞的传染病模型。文献［8］则引入一个常数来说明其他地域对所考虑地域的信息传播的影响。Huo等［9］主要研究了带有正面信息和负面信息影响的SEI模型。

本文在经典的SIS传染病模型的基础上，考虑媒体报道对该模型所产生的正面影响和负面影响，并分析了其前向和后向分支以及Hopf分支出现的条件。

1 模型的建立

假设在人口规模不变的情况下，将人口分为易感者、染病者 2类，分别用 S（t）、I（t）表示 t时刻的易感者、染病者的数量。M1（t）和 M2（t）分别表示t时刻关于传染病的正面和负面信息的数量。模型的传播过程如图1所示。

图1 SIS模型的传播动力图

由图1可得如下系统：

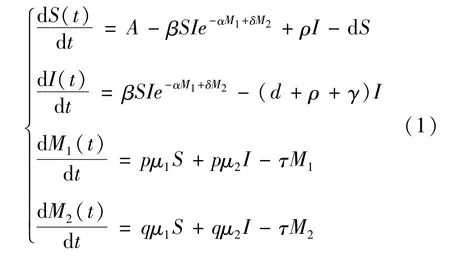
则t时刻的人口总数可表示为：N（t）＝S（t）＋I（t），其中所有的参数均为正数。式（1）中：A表示人口的输入率；d表示自然死亡率，本文假设所有个体的自然死亡率相等；γ表示因病死亡率；β表示个体从易感者变为染病者的传染率系数；α表示正面信息对传染病传播的减少率；δ表示负面信息对传染病传播的增加率；ρ表示染病者的恢复率；p表示传染病期间提供关于疾病正面信息的个体所占的比率；q表示传染病期间提供关于疾病负面信息的个体所占的比率；τ表示信息的失效率；μ1和μ2分别表示传染病期间易感者和染病者发布信息的发送率。

显然，系统（1）的可行域为 X＝｛（S，I，M1，M2）∈｝。则有下面的引理：

引理1 系统（1）在 X中是正向不变和有界的。

2 基本再生数的计算

由系统（1）容易得到其无病平衡点为：

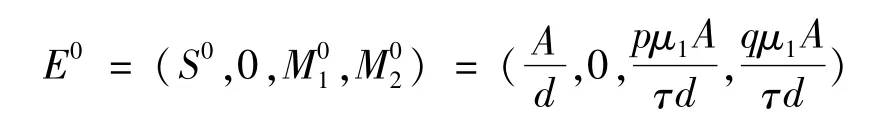
用下一代生成矩阵［10］的方法可以求出基本再生数：

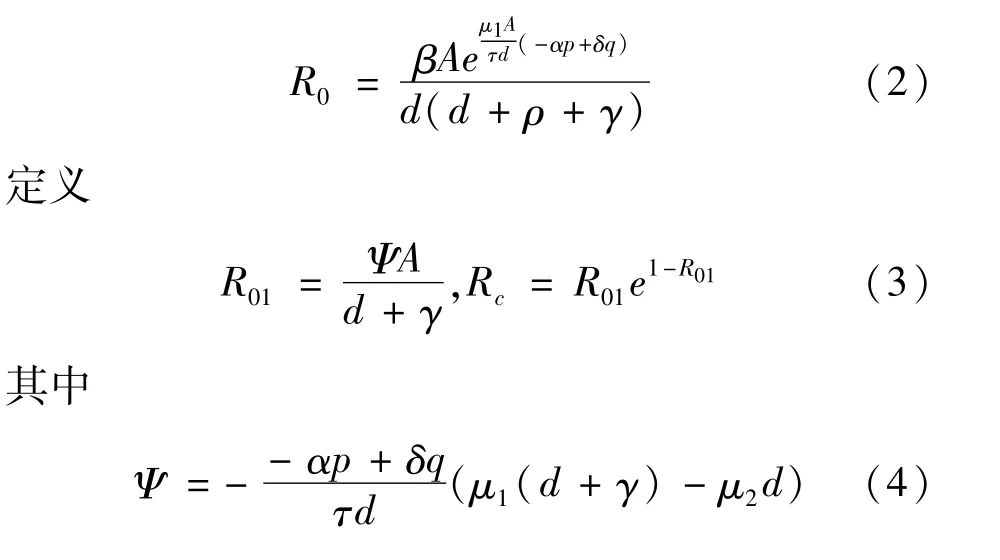
3 平衡点的存在性和稳定性

3.1 无病平衡点的存在性和稳定性

定理1 系统（1）的无病平衡点E0，当R0＜1时，E0是局部渐近稳定的；当R0＞1时，E0是不稳定的。

证明 系统（1）在无病平衡点处的特征方程为：

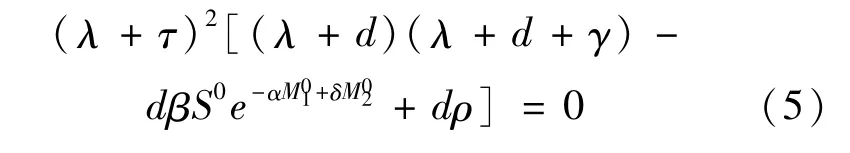
方程（5）的2个特征根分别为：λ1＝λ2＝-τ，另外2个由以下方程确定：

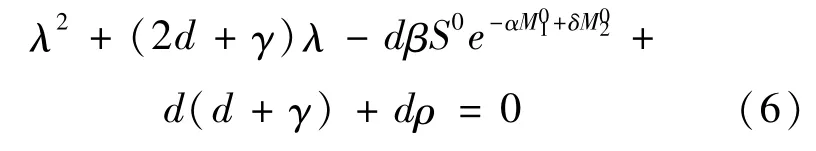
因此，由以上的计算和分析可以得到：

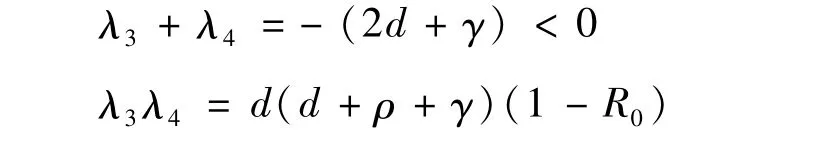
当R0＜1时，方程（6）有一对负实根，因此E0是局部渐近稳定的；当R0＞1时，方程（6）由2个符号相反的实根，此时E0是不稳定的。

3.2 地方病平衡点的存在性

定理2 对于系统（1）：

1）当 R0＞max｛1，R01｝时，它有唯一的正平衡点；

2）当 Rc＝R0＜min｛1，R01｝且 R01＞0时，它有唯一的正平衡点；

3）当 Rc＜R0＜min｛1，R01｝且 R01＞0时，它有2个不同的正平衡点和。

证明 不妨假设（S，I，M1，M2）＝（S*，I*，）满足系统（1）的右边均为0，计算可得

1）当R0＞1时，有φ（0）＝R0-1＞0，φ（∞）＜0。若 Ψ≠0，φ″（I）＝-Ψ2e-ΨI＜0，有 φ′（I）＜φ′（0），即 Ψe-ΨI＜Ψ，则

当 R0＞R01时，φ（I）＝0有唯一的正解。

若 Ψ＝0，由方程（7）可得

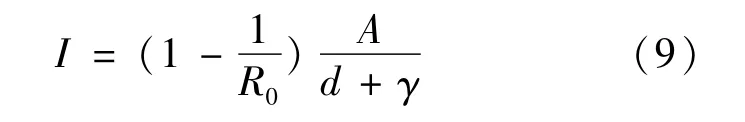
当R0＞1时I＞0。因此，可以求出正平衡点。

2）当R0＜1时，可以得到 φ（0）＝R0-1＜0，φ（∞）＜0。若 φ′（I）＝0，则有在此情况下，为了确保I为正，必须满足条件Ψ＞0和R0＜R01。更进一步，当且仅当R0＝Rc时，仍可得I是一个正解。因此，可以求出正平衡点。

3）在证明2）的基础上，当 φ（0）＞0时，R0＞Rc成立。此时满足。因此，可以求出正平衡点。证明完毕。

3.3 地方病平衡点的稳定性

1）当 R0＞max｛1，R01｝，a1（）a2（）-）＞0，a1（）［a2（）a3（）-）］-（））2＞0，a4（）＞0时，地方病平衡点是局部渐近稳定的；

2）当 Rc＝R0＜min｛1，R01｝且 R01＞0时，地方病平衡点是一个鞍结点；

3）当 Rc＜R0＜min｛1，R01｝且 R01＞0时，地方病平衡点是一个鞍点；

4）当 Rc＜R0＜min｛1，R01｝且 R01＞0时，地方病平衡点是一个结点。

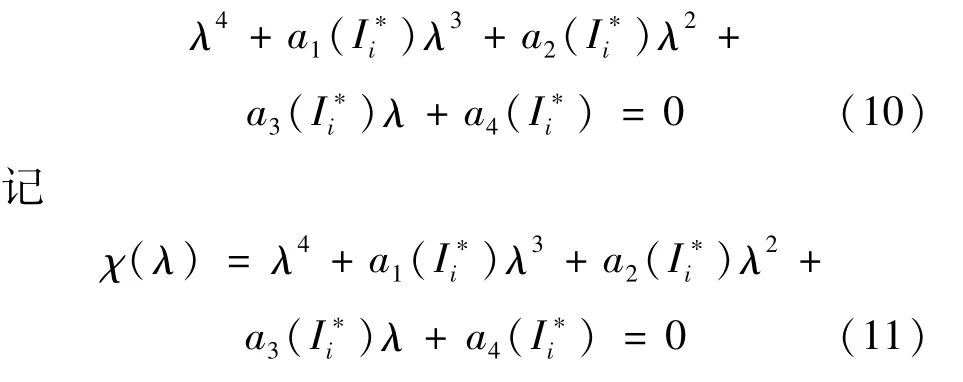
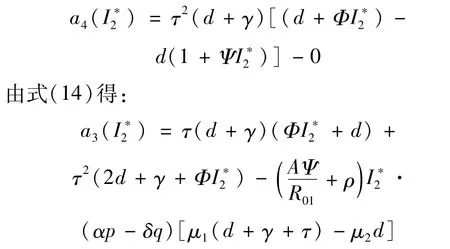
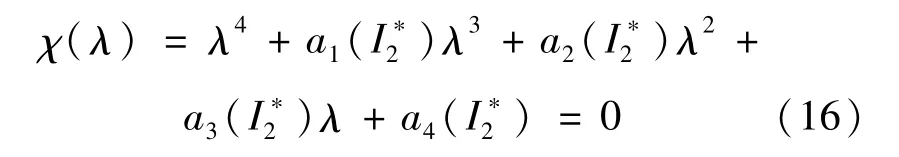
令 λj（）（j＝1，2，3，4）是方程（17）的根。

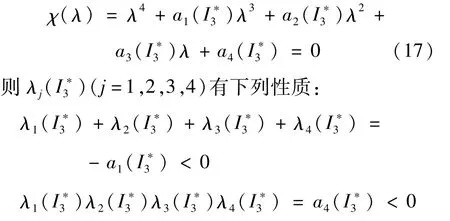
此时可知方程（17）有正特征根和负特征根。则系统（1）的地方病平衡点为鞍点。3）证明完毕。

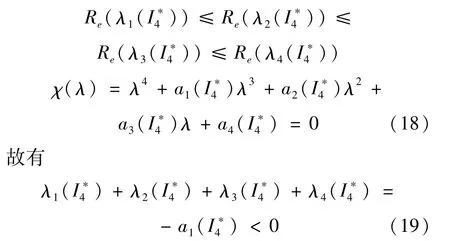
和 λ1（）λ2（）λ3（）λ4（）＝a4（）＞0。易知 λj（）＜0（j＝1，2，3，4）。不失一般性，不妨假设：

4 分支分析

4.1 前向分支和后向分支

定理4 当R01＜1且R0＝1时，系统（1）出现前向分支。当R01＞1且 R0＝1时，系统（1）出现后向分支。

证明 系统（1）在 E0处的 Jacobian矩阵J为：

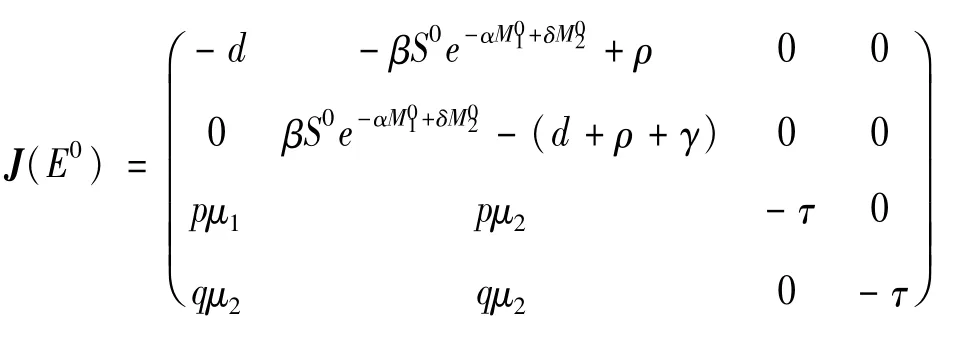
由文献［12］中的定理4.1可得R0＝1时的分支参数 β。因此，当β＝βm时，系统（1）在E0处的特征方程为

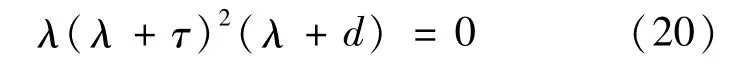
显然，0是一个特征根，对应于0的一个右特征向量为 η＝（η1，η2，η3，η4）T，其中：

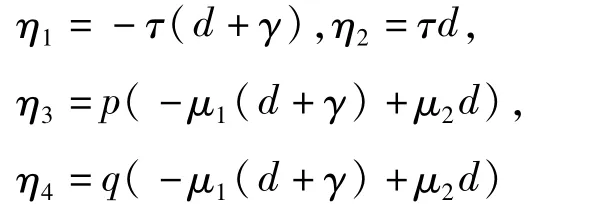
对应于 0的一个左特征向量为 ξ＝（ξ1，ξ2，ξ3，ξ4），且满足 ξJ＝0和 ξη＝1，于是有

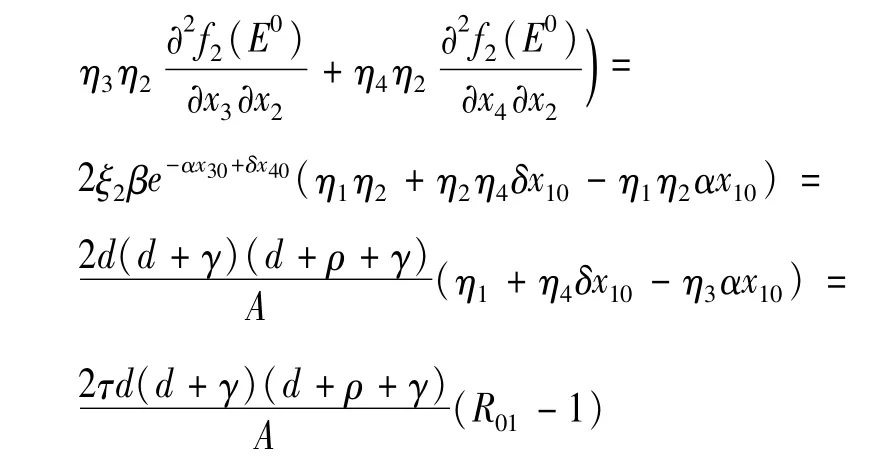
显然，M＞0恒成立，当且仅当 R01＞1时，N＞0。即当R01＜1且R0＝1时，系统（1）出现前向分支。当R01＞1且R0＝1时，系统（1）出现后向分支。

4.2 Hopf分支

定理5 令R0＞1，当β达到临界值β＝βc时，系统（1）在附近出现Hopf分支。

证明 不妨假设χ（λ）有2个实根x、y和一对复根 a±bi，其中 x＜0，y＜0且 a，b∈R。则

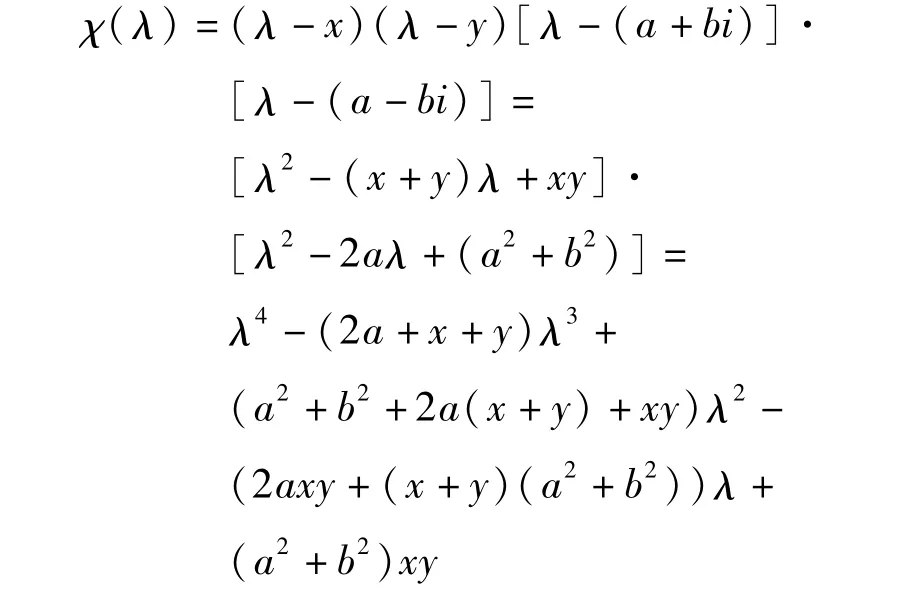
与式（11）进行比较，可得

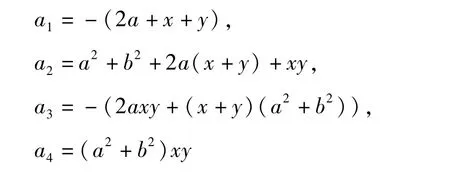
其中 ai＞0（i＝1，2，3，4）由式（12）～（15）给出。当χ（λ）＝0有一对纯虚根即a＝0时，可得

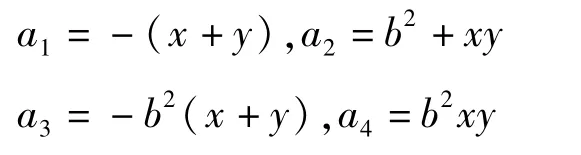
且 a3（a1a2-a3）-（a1）2a4＝0，这说明此时 β＝βc，即β＝βc和一对纯虚根的出现是一致的。把a＋bi代入式（11），可得χ（a＋bi）＝0。则 Re（χ（a＋bi））＝0，其中Re表示复数的实部。计算可得

由 a1、a2、a3和 a4的表达式可知，a1、a2、a3和 a4均含有β。故▽可以看作含有a和β的隐函数。则▽（a，β）＝0定义了一个自变量为 β的函数a（β）。对▽关于β求导，得＝0。故有。

接下来，沿着曲线β＝βm确定的符号。注意到a＝0和a2＝b2＋xy在曲线 β＝βm上，且a2、a3依赖于β，则可得

即当β到达临界值βc时，系统（1）在附近出现Hopf分支。证明完毕。

5 参数敏感性分析

通过分析可得

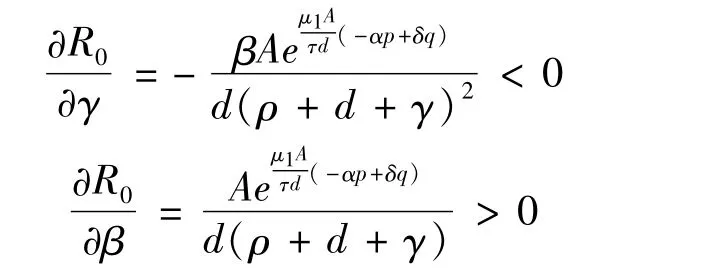
图2说明R0随着γ的减小而增大，随着β的增大而增大。图2所取的参数为：A＝0.8，β＝0.8，ρ＝0.2，d＝0.6，γ＝0.2，p＝2／3，q＝1／3，μ1＝0.8，μ2＝0.06，τ＝0.6。图3说明 α、δ和 R0之间的关系。根据

可知，R0与α成反比关系，R0与δ成正比关系。即在传染病传播期间，适当减少负面信息的影响和传播，或者增加正面信息的影响和传播，对于减少传染病的传播都是有重要作用的。图3所取的参数为：A＝0.8，α＝0.4，δ＝0.2，ρ＝0.2，d＝0.6，p＝2／3，q＝1／3，μ1＝0.8，μ2＝0.06，τ＝0.6。

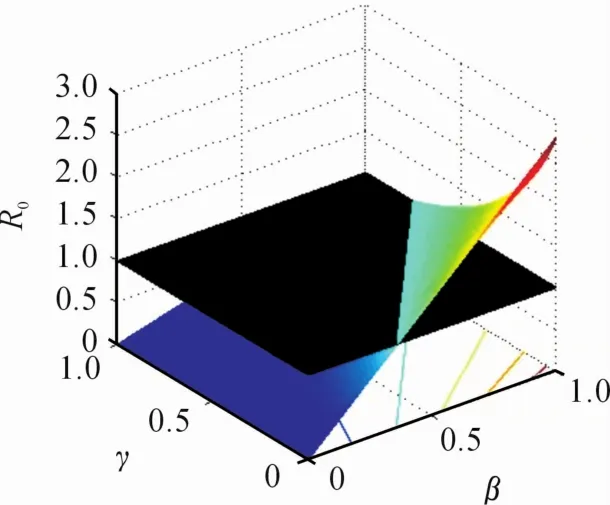
图2 R0与γ、β的关系

图3 α、δ和R0之间的关系

图4 说明当R01（＜1）减小时，前向分支会出现，地方病平衡点局部渐近稳定，而无病平衡点不稳定。对于给出的一组参数值，R0的值是确定的，当R0＜1时，染病者的数量会减小到0；当R0＞1时，染病者的数量会增加或减小到图中表示地方病平衡点的曲线。图5说明R01（＞1）增大时，出现后向分支，无病平衡点和较大的地方病平衡点局部渐近稳定。从流行病学的意义讲，后向分支的出现表明：仅仅使得基本再生数小于1是不足以消除某种疾病的。

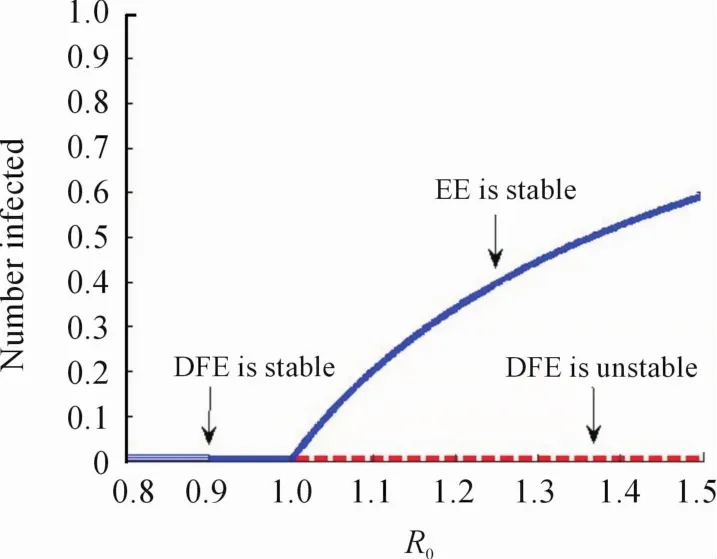
图4 前向分支

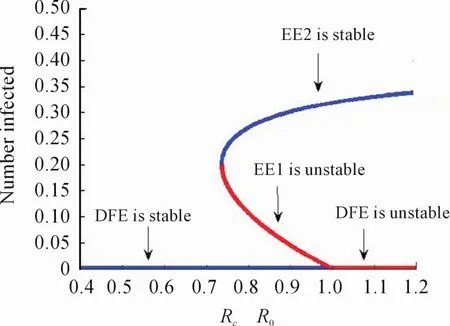
图5 后向分支

图6 把系统（1）与没有媒体影响的经典SIS传染病模型（α＝0，δ＝0）进行了比较，结果显示，媒体报道会影响染病者的数量。图7、8对参数进行了敏感性分析。从图中可以看出：当α增加时，染病者的数量会减少；当δ增加时，染病者的数量会增加。由此可见，媒体报道对传染病的传播有一定程度的影响。

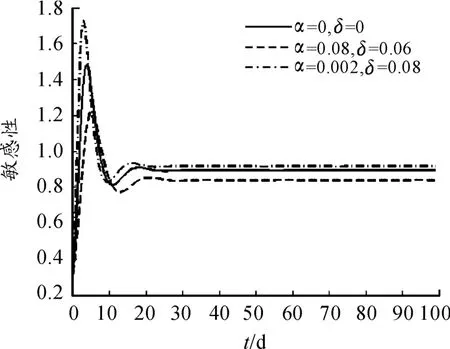
图6 系统（1）与没有媒体影响的经典SIS传染病模型（α＝0，δ＝0）的比较

图7 α敏感性分析

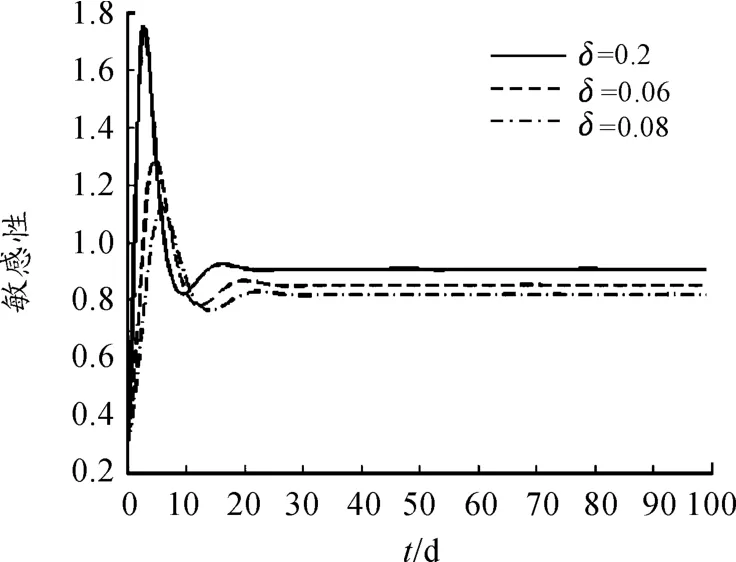
图8 δ敏感性分析

6 结束语

本文建立并研究了一类受媒体影响的传染病模型。分析了模型（1）的无病平衡点和地方病平衡点的存在性和稳定性。结果显示：媒体报道在降低传染病的传播速度方面能起到一定的作用。另外如果考虑到信息的滞后性，系统或许会产生更为复杂的动力学性质，这也是即将要开展的工作。