上市券商股CAPM模型适用性及收益影响因素研究

王 尧，杨克磊

（天津大学管理与经济学部，天津 300072）

对中国股市而言，2014年是不平凡的一年，上证综指年涨幅逾50%，成为亚洲资本市场榜首，创全球金融危机以来最佳表现。以券商股板块为例，年平均涨幅达160%，屡屡成为股民及媒体眼中的焦点，宏源证券、太平洋等涨幅更超过250%。在此大背景下，新股开户数持续增加，天量资金涌入，如何选择高收益的标的资产再次成为广大股民迫在眉睫的问题。在各种新方法层出不穷、众说纷纭的今天，我们不妨换个思维，重拾经典。

1964年，William Sharp［1］、John Lintner［2］和Jan Mossion［3］在 Harry Markowitz建立现代投资组合管理理论的基础上，将其进一步发展为资本资产定价模型（CAPM）。作为现代金融理论的三大基石之一，资本资产定价模型给出了确定资产风险及其期望收益率之间关系的精确预测方法［4］。在犹如过山车般的中国股市，CAPM模型能否为投资人提供一种选择标的资产的有效渠道，摒弃总风险，仅关注系统风险。如果CAPM模型在中国股市或其若干子板块具有适用性，也就是说，影响单只股票收益率的最主要因素是其与整个市场共同变化的程度，那投资者在牛市选择β系数高的股票，获得高于大盘平均水平的超额收益，在熊市选择β系数低的股票，在经济萧条的大背景下主动防御，使损失低于大盘平均水品，而β系数也是一个易于获取且具有横向可比性的指标；如果CAPM模型不具有预期中的适用性，那么影响某一类股票收益的因素都有哪些，该以何指标作为选择投资标的参考，也是值得投资者关注的问题。

1 概述

关于CAPM模型在我国股市的适用性，众多学者做了大量研究，但结果分为迥然不同的两派：文献［5］在深证A股中随机选择81只股票，通过时间序列检验和截面回归2种方法，得出CAPM模型在深证股票市场并不完全适用的结论。夏裴［6］、黄振等［7］学者均认为 CAPM模型在中国证券市场不适用。文献［8］随机选择了涵盖各大行业的47只股票，通过分析得出结论：CAPM模型在上交所具有较好的适用性，且β系数的拟合优度高达0.997，系统风险对股票收益率的解释能力很强。此外，文献［9］分析了CAPM模型在钢铁子板块中的适用性，得出钢铁行业β系数整体偏高的结论，在70%以上的钢铁股票中，系统风险对收益率有着较好的解释能力。陆艳［10］、表二苏等［11］也分别讨论了CAPM模型在移动通讯行业、银行业、电力行业、酿酒业等领域的适用性。

关于个股收益的影响因素，周孝华等［12］选择了537支个股在5年内的月度收益数据，通过研究发现：收益率与市值正相关，与股票市净率、净营运资产等负相关。厦门大学的张菁［13］研究了我国上市银行股收益的影响因素，发现银行股收益与账面市值比负相关，与市值呈现二次曲线关系。总的来说，券商股领域的CAPM模型适用性及收益影响因素研究都属于较空白的领域，而随着我国经济政策的更加开放以及资本市场的日趋完善，券商股板块的地位更加重要。本文的研究将在一定程度上弥补现有研究的不足，对券商股领域的行情分析及投资策略都有一定的现实和理论意义。

2 数据与方法

2.1 研究思路

本文拟选取我国A股上市的21支券商股，其中国信证券于2014年12月29日开始上市交易，故不在本文的研究范围。研究时间为2012年1月1日—2014年12月31日，首先利用20支股票在这3年以来的收盘价，计算以周为单位的收益率，利用定义式求取20支股票的β系数并通过在时间序列上回归的方法进行验证，通过分析β系数研究我国券商股收益率对系统风险的敏感程度。再用157个时间点的横截面数据，以β系数作为自变量，个股收益率作为因变量进行线性回归，来验证β系数与个股收益率的线性关系及其对收益率的解释能力，从而得出CAPM模型对我国上市券商股是否适用的结论。若适用，则为投资者提供了一种简单可靠的标的资产选择方法；若不适用，进而讨论上市券商股收益率的影响因素。

2.2 研究方法

CAPM模型适用性的实证研究一般采用历史数据，构建模型（1）：

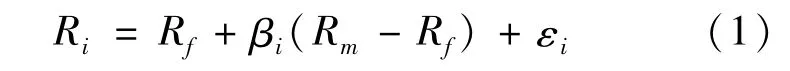
其中：Ri表示资产i的收益率；Rf表示无风险收益率；Rm表示市场收益率；βi表示资产i的β系数；εi为其他因素影响的度量。在同一时点下，Rm、Rf均为常数，若已知每个βi及其对应的Ri，便可进行回归。

以往的研究中，β的计算均采用历史数据回归，而没有采用定义式直接计算。为了提高数据的准确性，本文打算采用定义及回归2种方法分别计算，再以两者的平均值作为最终的β系数。得到β系数之后，就可作为模型检验中的自变量，采用横截面数据，对同一时点一系列股票的β系数和收益率进行回归，并进行检验，对模型（1）通过变形得到如下形式：

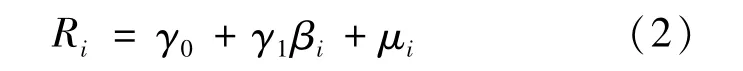
根据回归结果就可得到结论。

2.3 样本选取

本文样本采用在我国A股上市的20家券商股，信息见表1。另从国泰安数据库（CSMAR）获得这20家上市券商从2012年1月1日—2014年12月31日每个交易日的收盘价作为基础数据。

2.4 变量计算

2.4.1 收益率的时间间距

根据模型，首先需要确定时间间距t。计算β系数并验证CAPM模型适用性的过程是对大量的历史数据进行回归的过程。就回归分析的方法本身而言，样本容量越大，回归的效果越好。但是在较短的时间内，交易信息中可能包含偶发事件造成的噪音影响，为了既得到足够的样本量，又能剔除噪声波动的影响，使数据真实可靠，必须将2个维度综合考虑。本文选取的数据是2012年1月1日—2014年12月31日之间每个交易日的交易数据，时间间距t设为1周（一般为每周五的收盘价，如遇法定节假日则选择距离周五最近的一个交易日的收盘价），于是得到157组收益率指标。

2.4.2 市场收益率

公式中的Rm是指市场收益率，通常用股票价格指数的平均收益率来代替。股票指数本质上是通过选取一组有代表性的股票来描述整个股票市场总的价格水平的变化，是整个股票市场的缩影，因此以股票指数的收益率替代理论上的市场收益率是可行的。我国股市中现有上证180指数、沪深300指数、央视50指数、上海证券综合指数（简称上证综指）、深证股票综合指数等，它们分别从不同的方面反映股票市场的价格走势。根据实际生活及研究中的习惯及指数本身的适用范围，本文以上证综指和深证成指为依据计算市场收益率：

指数收益率＝（当期收盘指数-上期收盘指数）／上期收盘指数

本文将上证综指和深证成指的收益率取平均数，定义为综合市场收益率Rm：

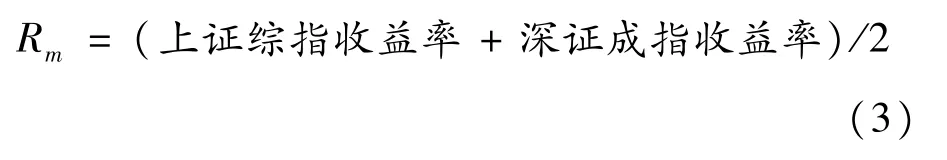
2.4.3 股票收益率

利用式（4）可计算时间间距t下的157组券商股周收益率。

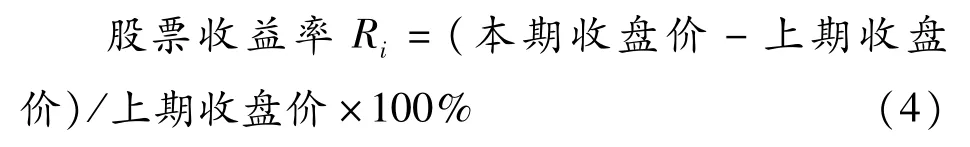
为了剔除股票除权除息对价格的影响，本文采用的收盘价均为复权价格。此外，在研究期内，5家股票因重大事项停牌，造成一部分期间内交易数据的缺失，且西部证券于2012年5月3日上市交易，在此之前也没有交易信息。为了减少缺失的交易数据对分析结果的影响，在根据定义计算β系数以及回归过程中，本文对缺失的部分直接从样本中予以剔除，剔除数据最多的宏源证券剩余117组数据，仍属于大样本，认为数量减少对计算结果不会造成实质性差异。

2.4.4 无风险收益率

无风险利率是指将资金投资于某一项没有任何风险的投资对象而能得到的利息率，这是一种理想的投资收益。在金融资产的定价研究中，无风险利率一般指投资者可以在此利率下进行自由借贷。国外的实证研究中多以短期国债利率或银行同业拆借利率来代替。在文献［14］中，指出了我国债券交易市场不统一、期限结构不合理，以及银行同业拆借利率隐含了银行自身经营风险等缺点，因此无法利用成熟资本市场中的方法选择无风险利率。考虑到我国居民仍以储蓄作为最主要的投资方式、大型商业银行违约率极低以及央行指导利率的高适用性，本文拟用银行存款利率代替无风险利率，且我国股市多以短线持有赚取资本利得为主，故选择3个月定期存款利率，定义为Rf。

2.4.5 β系数

如本文所述，β系数的定义式为

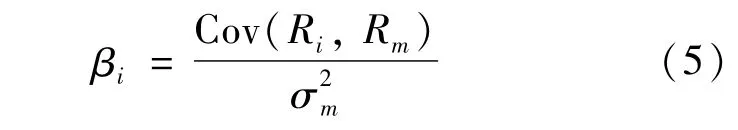
已知Rm和Ri（其中i为1～20支券商股股票），利用excel自带的covar和varp函数公式可求得20支券商股的β系数。对模型（1）适当变形得到如下模型：

这个回归方程通常被称为“一次回归”方程，在每一个时点 t下，Rmt＝Rm-Rf，而 Rit＝Ri-Rf，对每一支股票的收益率Rit与均衡市场组合的收益率Rmt进行时间序列的回归，也可得到一组β系数，将2组数据求平均数，从而得到最终的 β系数。

3 实证分析与检验

3.1 β系数的实证分析与检验

要利用历史数据回归求得β值，首先要求模型（6）中的Rit和Rmt线性关系成立，并进行异方差与序列自相关的检验。

用SPSS18处理数据并得到如图1所示结果。

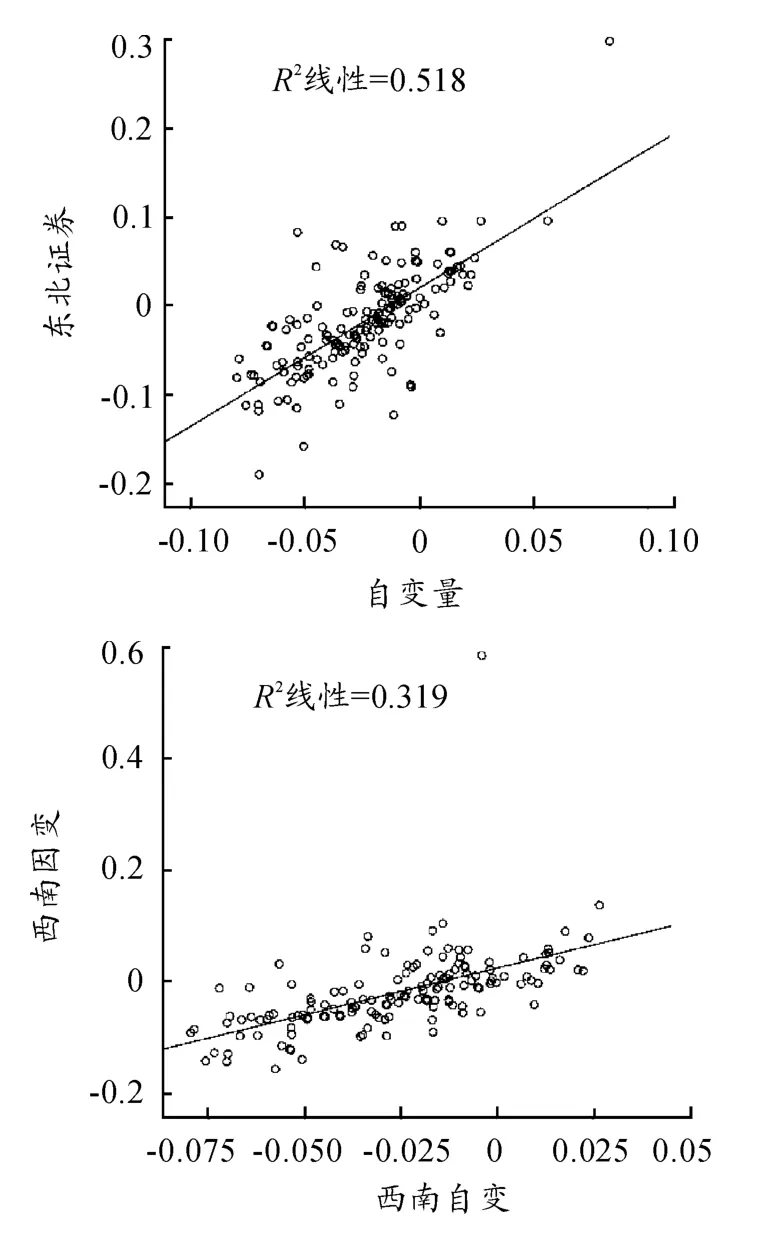
图1 异方差检验的散点图

用图示法进行异方差的检验（如图1所示），分别做出20支股票自变量和因变量的散点图，如果模型（1）中的随机项εi存在异方差，则随着自变量的增大，因变量偏离回归直线的离散程度将增大，使得点集呈现出三角形状或哑铃形状。观察图像发现，散点与拟回归直线之间没有明显的递增或递减的偏离趋势，则说明模型中的随机项是同方差的。

进行序列自相关检验，给定显著性水平α＝0.05，查Durbin-Watson分布表，当样本容量为T＝157时，得到临界值 dL＝1.72，dU＝1.747。

当0＜d＜dL时，说明随机项存在一阶自相关；当4-dL＜d＜4时，说明随机项存在一阶负自相关；当dU＜d＜4-dU时，说明随机项不存在一阶自相关；当dL＜d＜dU或4-dU＜d＜4-dL时，则不能判别随机项是否存在1阶自相关。

再观察可见，R2的平均值为0.51，T值的平均值为12.77，最小值为5.8，说明线性关系显著且自变量对因变量有很高的解释能力，说明回归效果较好，结果可信。用回归方法得到的β值和定义式求得的β值平均后得到20只股票最终的β系数，见表2。

3.2 CAPM模型适用性的实证分析与检验

得到每一支券商股的β系数之后，就可以在157个时间点分别用β系数和与之对应的收益率进行横截面上的回归，结果描述如表3所示。

表2 β系数的计算结果

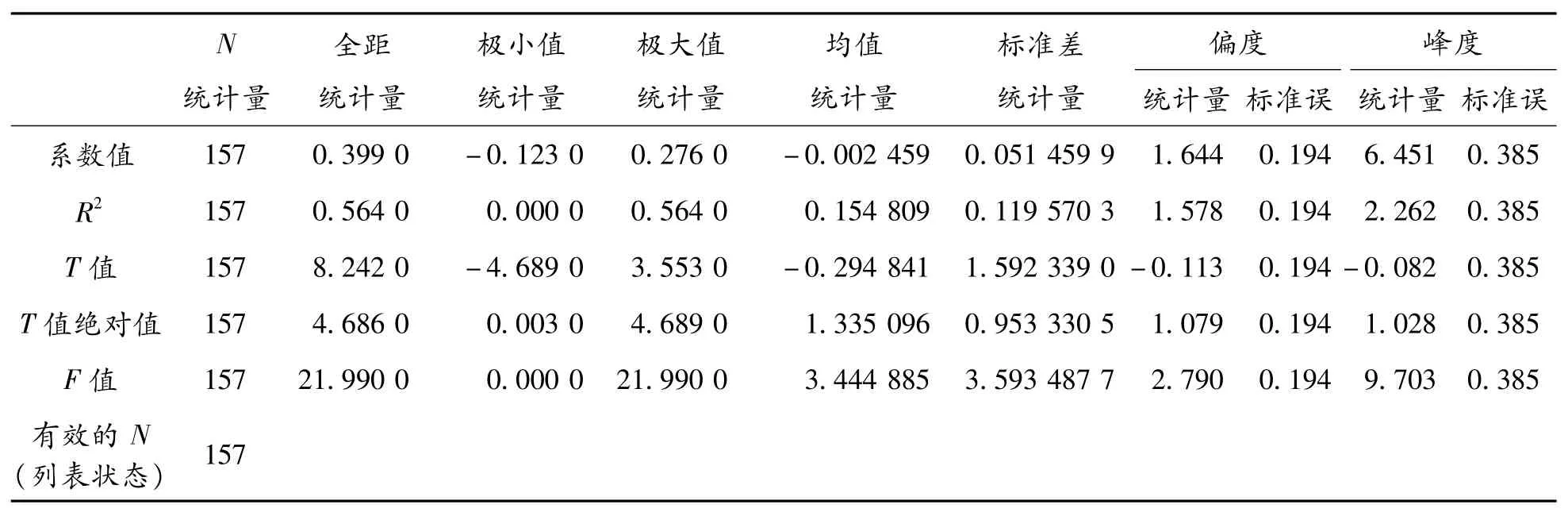
表3 CAPM模型回归结果的描述统计量

R2的平均值为0.155，拟合优度不理想，说明β值对个股收益的解释能力平均只有15.5%。进行回归参数估计值的显著性t检验，T绝对值的平均值为1.335，勉强通过显著性水平α＝0.10时的检验。即当α＜10%时，β系数对股票收益率没有显著的线性关系；当α≥10%时，线性关系成立。在157组数据中，T值绝对值大于临界值的有87组，占比55.41%。在模型的整体显著性检验中，F的平均值为3.44，而α＝0.1时，自由度为（1，18）的F分布的临界值为3.01，则模型整体在α＝10%的水平下显著。

3.3 券商股收益率影响因素的实证分析

通过上一步的分析，发现β系数虽然与股票收益率线性相关，但对其解释能力仅有15%，因此仍然有其他因素能够影响个股收益。根据Fama-French的三因子模型，认为上市公司的市值、账面市值比、市盈率可以解释股票收益率的差异，因此定义并引入如下变量。

市值（SZ）等于每一个时点下，股票市场价格乘以股份数的积，因为我国股权分置改革的最终目的是实现股份的大流通，因此此处的股份数是指企业账面中的股本（实收资本），包括流通股和非流通股；账面市值比（ZM）是指该时点下所有者权益总额与市值的比，此处的账面权益应包括实收资本、资本公积、未分配利润以及少数股东权益等；市盈率（PE）等于当前市价除以每股收益。

每一个时点的收益率为本时点的收盘价较上一时点收盘价的涨（跌）幅（例如2014年中期收益率是2014年6月30日股票收盘价较2013年12月31日股票收盘价的涨幅），根据20家券商的财务数据，计算上述变量的值并分别与股票收益率进行回归，结果如表4所示。

在显著性水平α＝0.05，T＝20，k＝1的情况下，随机项不存在1阶自相关的DW值范围为（1.41，2.59），则所有回归方程均不存在序列自相关。市值与收益率回归结果的R2为0.05，拟合度非常低，T值绝对值为0.882 2，F值为1.049 8，模型整体及参数估计值均不显著；账面市值比、市盈率与收益率的回归结果均不能通过F检验及T检验。考虑现实情况中，投资者获得财务报表信息后会影响其投资意愿，而投资意愿的改变造成股票价格的变动，最终影响到下一期的收益率，也就是说本期的财务信息并不能立刻被投资者吸收并反映在本期的收益率上，而是会影响下一期的收益率，按照此种思路将收益率滞后一期再与市值、账面市值比和市盈率等自变量回归。

新的回归结果中，市值作为自变量的回归仍然不能通过F检验和T检验；在α＝0.1的显著性水平下，T（18）的临界值为 1.33，F（1，18）的临界值为3.01，则账面市值比、市盈率与收益率的线性关系显著，且对收益率的解释能力分别为15%和19%，均是影响股票收益率的重要因素之一。

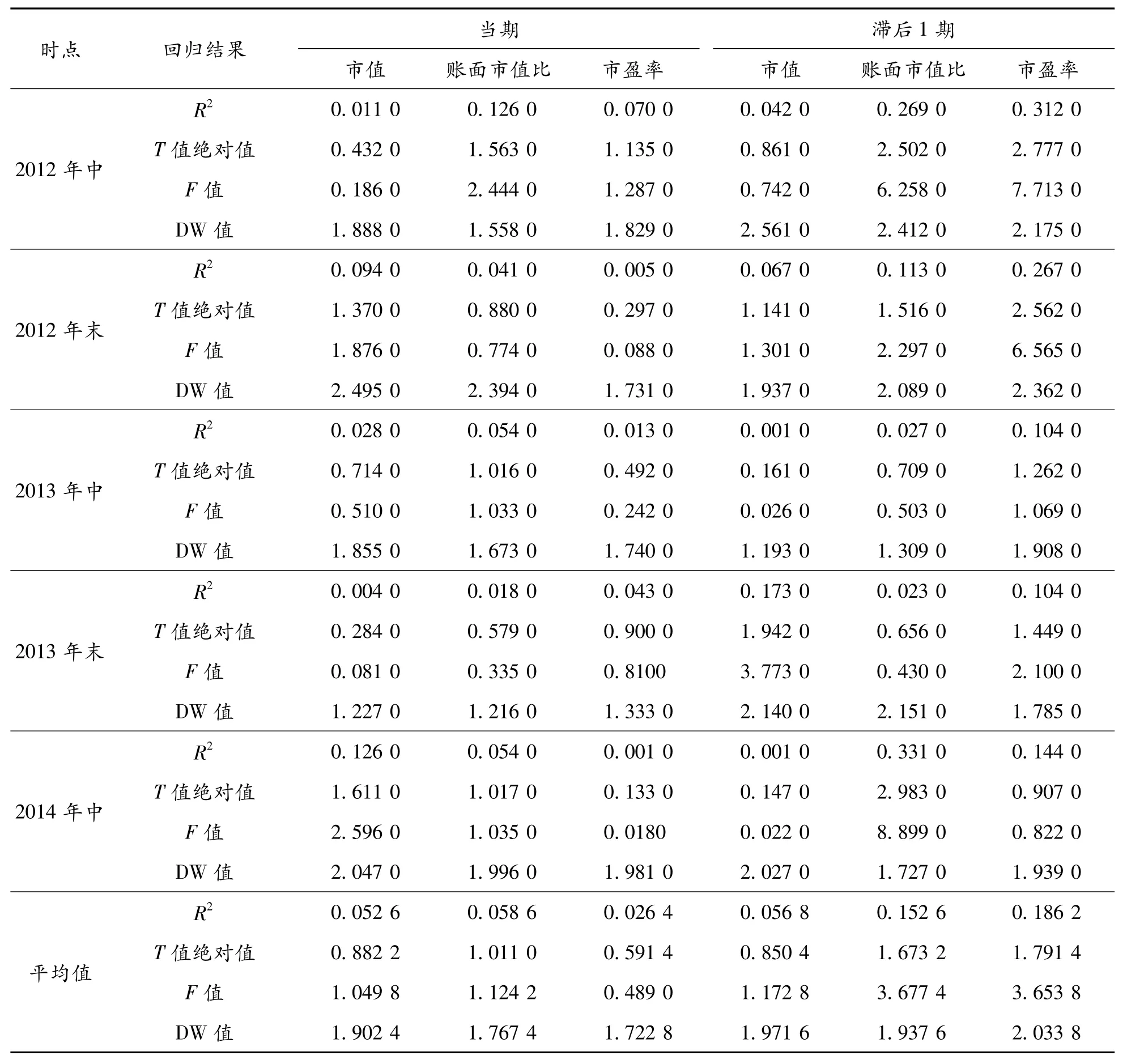
表4 收益率影响因素的回归结果

4 结束语

根据本文实证分析，发现券商板块股票的β系数整体偏高，平均值为1.724 3，最大值为华泰证券2.035，仅有的β系数小于1的锦龙股份为0.901，而其低于1的主要原因可能是虽然锦龙股份在股票分类中属于证券板块，但其仅仅是控股中山证券、参股东莞证券，其主营业务一半是自来水业务，并非真正意义上的券商股。券商股β系数整体偏高说明其波动程度远高于大盘平均水平，风险高、投机性强、对信息的反应敏感且剧烈。而券商股在股市的实际表现也确实如此，无论是在沪港通、央行降准等利好消息下的带头疯长，还是在原油走熊、资本监管等利空消息下的集体跳水，尤其是在2015年初的119暴跌中，券商股板块集体跌停，充分体现了券商板块是整个股市的“风向标”，作为牛市的带头大哥，现阶段值得投资者关注。

从本文3.2节的实证分析来看，CAPM模型在我国现阶段的券商股板块适用性并不很高，系统风险对收益率变动的解释能力不足20%，虽然通过了参数估计值的显著性T检验，说明β系数确实影响收益率，但绝非主要因素，投资者在选择标的资产时，可参考其β系数，但不应该将其作为主要的选择标准。

通过本文3.3节的实证分析可见：Fama-French的三因子模型并不完全适用我国现阶段的券商股板块，市值对收益率并没有显著的影响，而账面市值比和市盈率对滞后一期的收益率有一定的影响，但解释能力均小于20%。

综上所述，CAPM和三因子两大经典模型适用性欠佳，再次说明我国资本市场发展尚不成熟，投资者机构畸形，以个人为主体；投资观念不成熟，以盲目投机为主，羊群效应显著；信息披露不充分，大小投资者之间存在信息不对称；股权结构不合理，行政干预过多。在这样一个不成熟的市场，投资者切忌根据简单的模型和单个指标选取标的资产，应该综合考虑账面市值比、市盈率等多个指标，并密切关注经济大环境下股票市场整体的牛熊行情，充分利用 β系数增加收益、规避损失。