运用贝叶斯方法的混合异方差模型的参数估计

朱 莹，陈 萍

（南京理工大学理学院，南京 210094）

在一开始，描述股票价格波动等金融现象最常用的模型是随机游动模型。随着时间的发展，随机游动模型在应用中逐步暴露它的局限性：它无法解释金融变量波动的集聚性特征，因为股价或者其他类似金融产品的变化率不仅随时间t变化，而且常常在某一时段出现偏高或偏低的情况。1982年，Engle［1］提出了 ARCH模型（自回归条件异方差模型），并将其运用到英国通货膨胀特征的描述中。后来，Bollerslev［2］将这一模型进行推广，提出的GARCH模型（广义自回归条件异方差模型）被认为是最能集中反映方差变化特点而被广泛应用于金融数据时间序列分析的模型，该模型同时被广泛应用于验证金融理论中的规律描述以及金融市场的预测和决策中。非线性时间序列还往往呈现多峰、异常点、极端值等现象，这时单一的异方差模型很难给出精确的预测结果，而混合模型能很好地捕捉波动的聚集性以及金融数据所呈现的高峰厚尾和极端值的统计特征。基于此，本文建立混合异方差模型［3］来对经济领域中出现的复杂现象进行有效的分析研究。

1 混合正态异方差模型

Ft-1表示直到t时刻的信息，

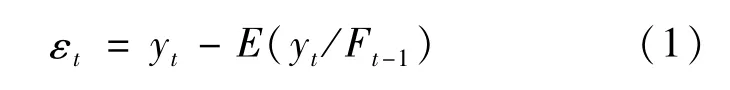
εt的条件分布由K个分布组成

Φ（·）是高斯分布，πk表示分布的概率，称之为混合正态异方差模型。εt是由以概率 π1，π2，…，πK的K个条件分布组成的，且：

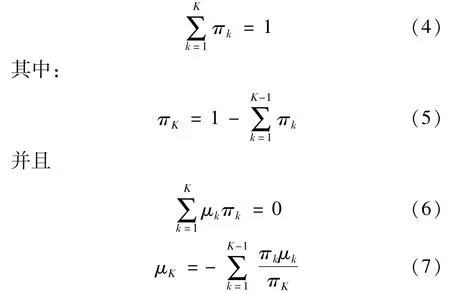
不过 ＝0并不意味着对称分布，只有当μK均为0才会发生。

从计量经济学的角度来看，混合正态分布是具有吸引力的，因为它的创新项εt是由K个条件方差方程组成的。因此，没有路径依赖问题，所以似然函数的估计是可能的，请注意，要有一个弱平稳的总体方差过程，只需要一个条件方差过程弱平稳即可。只要其他K-1个条件方差过程概率不太高，就被看作是爆炸性的。更正式的说，模型弱平稳条件［4］是

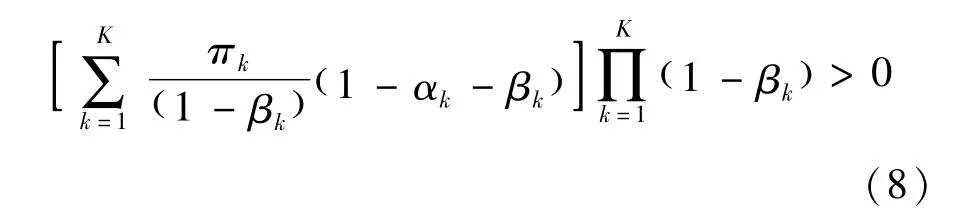
当改变有限混合分布中的顺序时，模型的似然性不变。如果需要对这些参数进行财务解释的话，可对参数增加π1≥π2≥…πK的限制。

1.1 混合正态异方差模型下的资产收益

假设股票价格St过程服从：

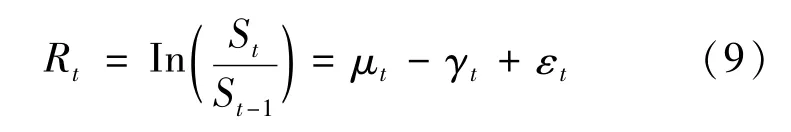
其中：εt／Ft-1～D（0，）；St是 t时刻股票价格；表示t时刻对数收益的条件方差；γt表示平均校正因子，它可以保证收益率的条件期望：

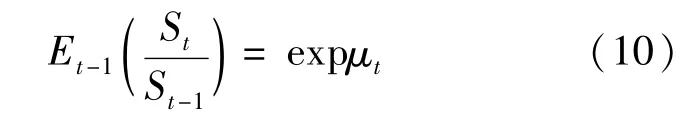
其中μt可以理解为预期的总回报率。式（8）中εt的条件矩母函数为：

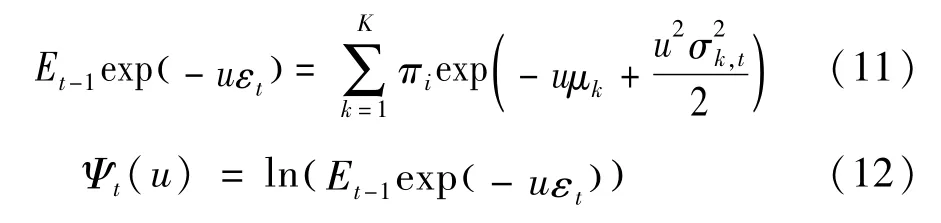
Ψt（u）表示条件累积量生成函数（即条件矩母函数的对数），所以有：

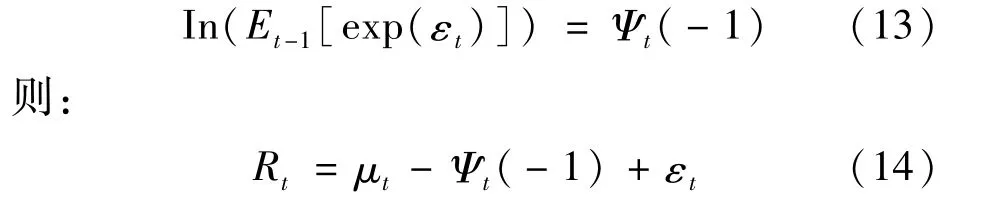
1.2 风险中性状态下的混合正态异方差模型下的资产收益

Rt的条件分布一旦给定，就可以直接代入数据。但最终目标是期权定价，则需要进一步计算。进行期权定价，需要一个等价鞅测度（EMM）。在这个测度下的预期总收益率等于无风险利率，即贴现后的收益为鞅。

在目前情况下，市场是不完整的，因此不存在恒定波动率BSM模型中独特的等价鞅测度。可以通过采用Nadom-Nikodym导数的规范来指定等价鞅测度。因此，期权价格由于Nadom-Nikodym导数的选择又是独特的。因为原始的测度和转变之后的测度必须有相同的空集，才能保证2种测度等价。在分布上加上上标Q来与原始分布进行区分，称之为风险中性测度Q下的分布或者简称为风险中性测度。

给定一个序列｛υt｝，定义 Nadom-Nikodym导数为：

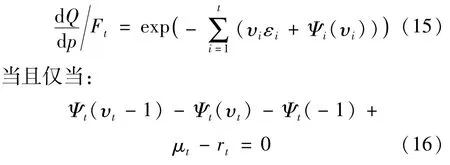
Nadom-Nikodym导数定义的测度Q是等价鞅测度，那么式（11）可以改写为：

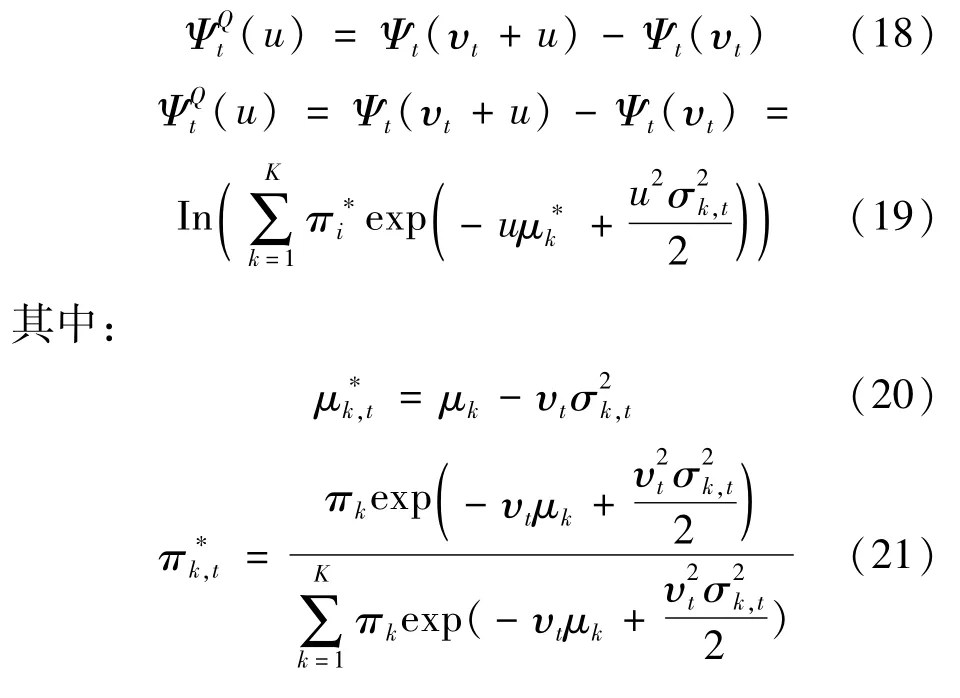
2 混合正态异方差模型下的贝叶斯参数估计

马尔科夫链蒙特卡罗（Markov Chain Monte Carlo，MCMC）方法己经成为一种主要的贝叶斯计算方法。一方面是由于它处理复杂问题的效率非常高，另一方面是由于它的编程相对容易。在贝叶斯分析应用中，最为广泛的MCMC［5］方法主要有Gibbs抽样方法和Metroplis-Hastings（简称MH）方法等。MCMC的研究为推广贝叶斯方法的应用开辟了广阔的前景，成为近几年时间序列分析以及计量经济学的重要研究课题之一。

根据式（17）的要求，模型的收益被规定为：

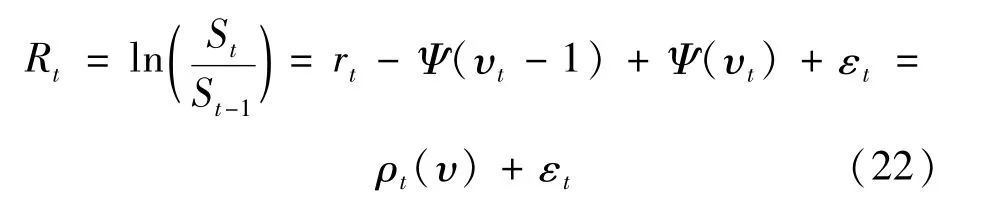
其中，T时刻观察值的似然函数［6］可以表示为：

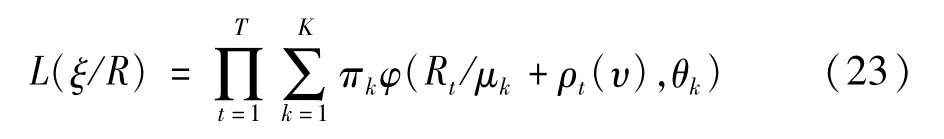
式中：ξ表示 υ，πk，μk，θk，k＝1，…，K组成的参数；R＝（R1，R2，…，RT）′表示收益向量；φ（Rt／μk＋ρt（v），θk）表示均值是 μk＋ρt（v），方差为依赖于θk＝（ωk，αk，βk）的

由于似然函数形式的复杂性，直接进行参数估计非常困难。考虑给每个观察值引入一个状态变量 Gt∈｛1，2，…，k｝，如果 Rt属于分布 K，则该状态变量就取值K。假设状态变量与给出的概率分布独立，那么Gt＝K的概率等于πk，可以写成：

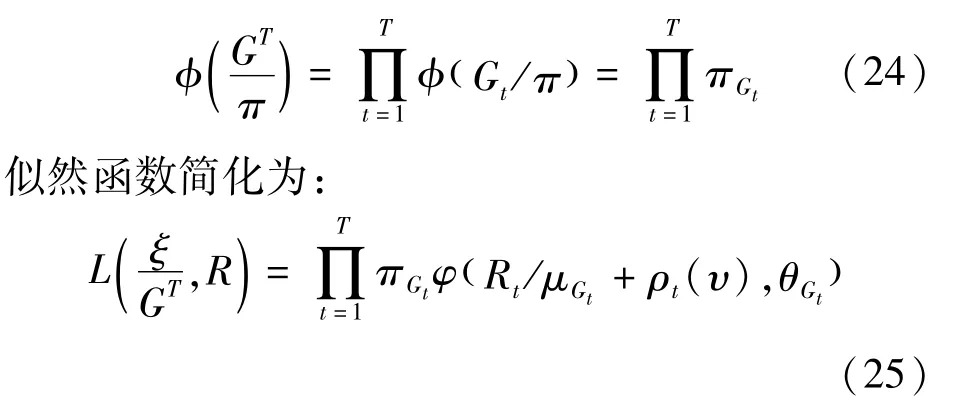
因为和的形式消失了，所以比式（23）便于计算。由于Gt没有被观察，可以把它作为模型的额外参数。尽管现在模型包含了更多的参数，但通过MCMC方法进行推断将会更加简单。

下面采用MCMC方法，用Gibbs抽样的方法，通过从参数的后验条件分布中抽样来得到后验分布的抽样。

联合后验分布为：

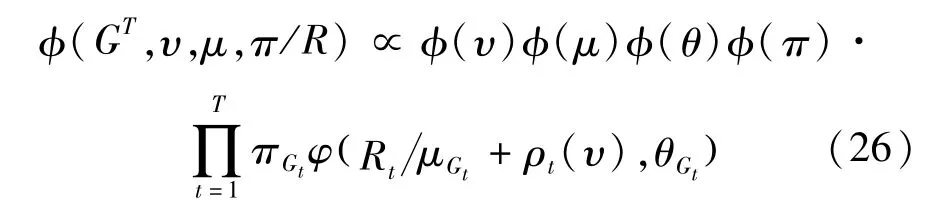
φ（υ）φ（μ）φ（θ）φ（π）为先验分布，并且假设它们独立，且K已知，采用Gibbs抽样如下：

1）φ（GT／υ，μ，θ，π，R）抽取 GT

由于GT之间相互独立，条件后验密度可以表示为：

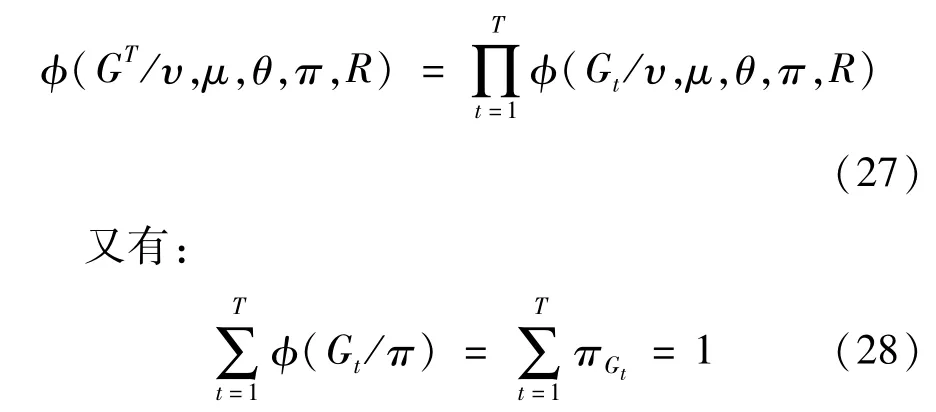
因此，｛GT｝可以看作多项分布，我们可以从下面的多项分布中抽取GT：

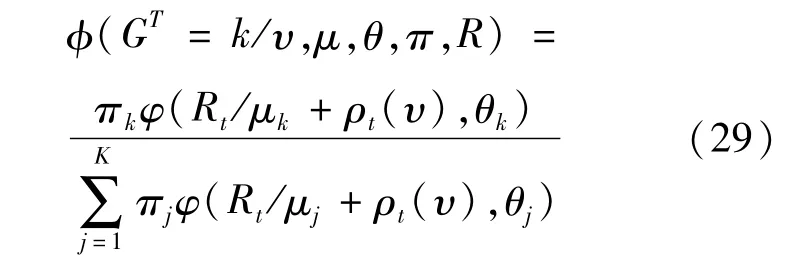
抽取GT时，可以先从均匀分布U［0，1］上随机抽取U，根据抽取U的利用多项分布得到相应的k，则完成GT的抽取。

2）φ（π／GT，υ，μ，θ，R）抽取 π

π的完全条件后验密度 φ（π／GT，υ，μ，θ，R）中，π的大小仅与GT有关，即：

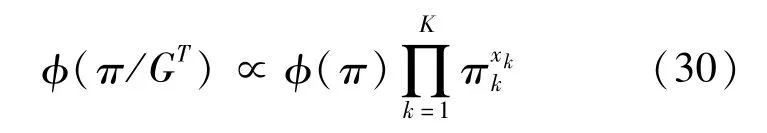
xk是Gt＝K的次数，π的先验分布φ（π）选择为Dirichlet分布，则其全条件后验分布服从Dirichlet（a1，…，ak）分布，ak＝ak0＋xk。

3）φ（μ／GT，υ，π，θ，R）抽取 μ

记 ~μ＝（μ1，…，μK-1）′，则条件分布 φ（μ／GT，υ，π，θ，R）服从多元正态分布，并且如果抽取了 ~μ，则μK可以从公式（7）中取得。

条件分布是均值为-A-1b，协方差矩阵为A-1的高斯分布：

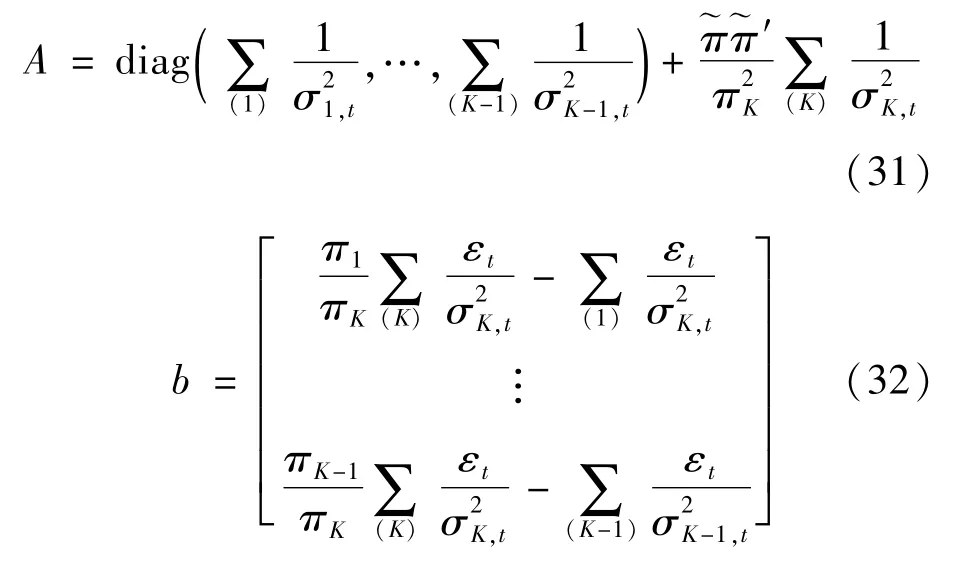
4）φ（θ／GT，υ，μ，π，R）抽取 θ

假定θk之间独立，即：

5）φ（υ／GT，θ，μ，π，R）抽取 υ

υ的条件后验分布不属于任何已知的分布族，由于υ是向量，可以在均匀分布U（0，1）中绘制一个观察值并找到υ的条件后验分布的对应分位数。

为了计算期权价格，首先需要去预测在Q测度下的收益密度，对于给定的样本R1，R2，…，RT，模型的一步超前预测密度RT＋1为：

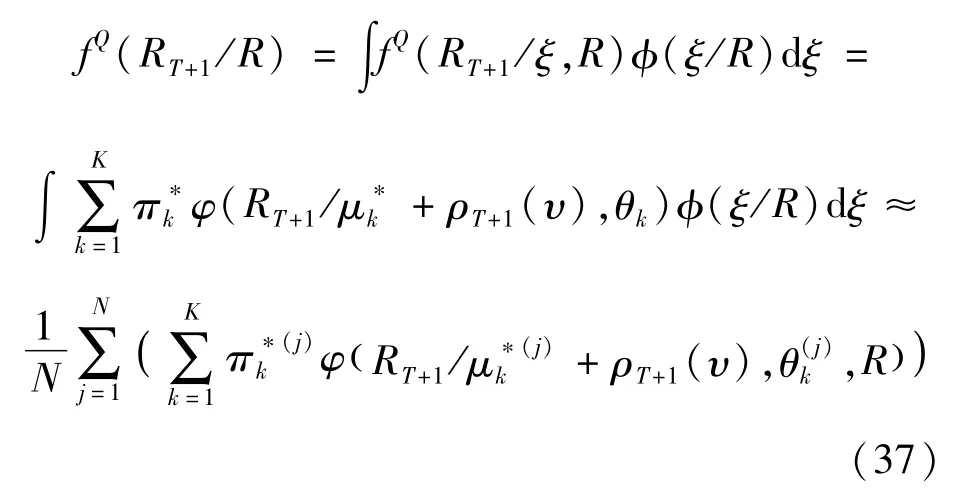
直到这里描述的预测密度是收益密度，为了获得预测期权价格，需要期权交易到期日的价格密度，这种预测的价格密度是通过将预测的收益汇总到n个到期日为止，对于欧式期权［7］来说：

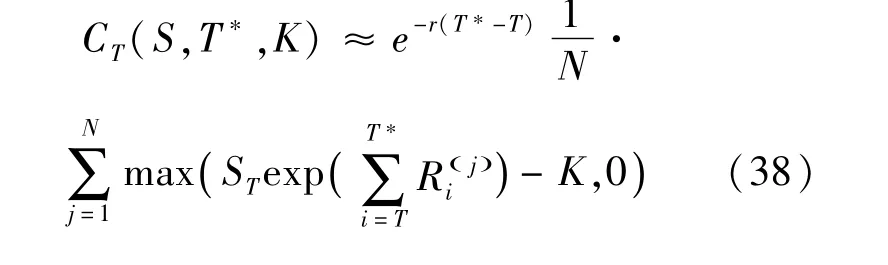
3 实证分析

2004年1月2日，上交所编制发布了上证50指数［8］。它主要由上海证券市场中具有较大规模和较好流动性的50支最具代表性的股票组成样本股。2005年2月23日，上证50ETF（华夏上证50ETF上市。它是基于上证50指数的交易型开放式指数基金。2015年2月9日，上海证券交易所正式推出了上证50ETF期权。它是上证50ETF为标的物的股指期权，是我国证券市场的第1个股指期权产品，填补了我国证券交易所期权产品的一大空白。本文选取上证50ETF 2017年1月3日—2017年12月29日242个交易日的日收益率数据进行参数估计，并且对2018年1月2日至31日的1 567份看涨期权进行期权定价误差的分析。

在混合正态模型中，有限混合分布中的个数还没有固定，事实上发现当K＝3时，它的概率非常小，趋近于零，可以忽略不计，因此K＝2被认为是最优的。本文利用stata和EViews软件进行估计［9］得到的参数估计结果见表1。

表1 参数估计结果

根据看涨期权的在值程度和剩余期限t分别将样本数据分类，见表2。

从表3中数据可以观察出模型的定价误差都不是很大，从剩余期限角度来看，剩余期限小于60天比天数大于60天的定价误差都要小，从在值程度的角度来看，深度实值期权的定价误差要更小一些。

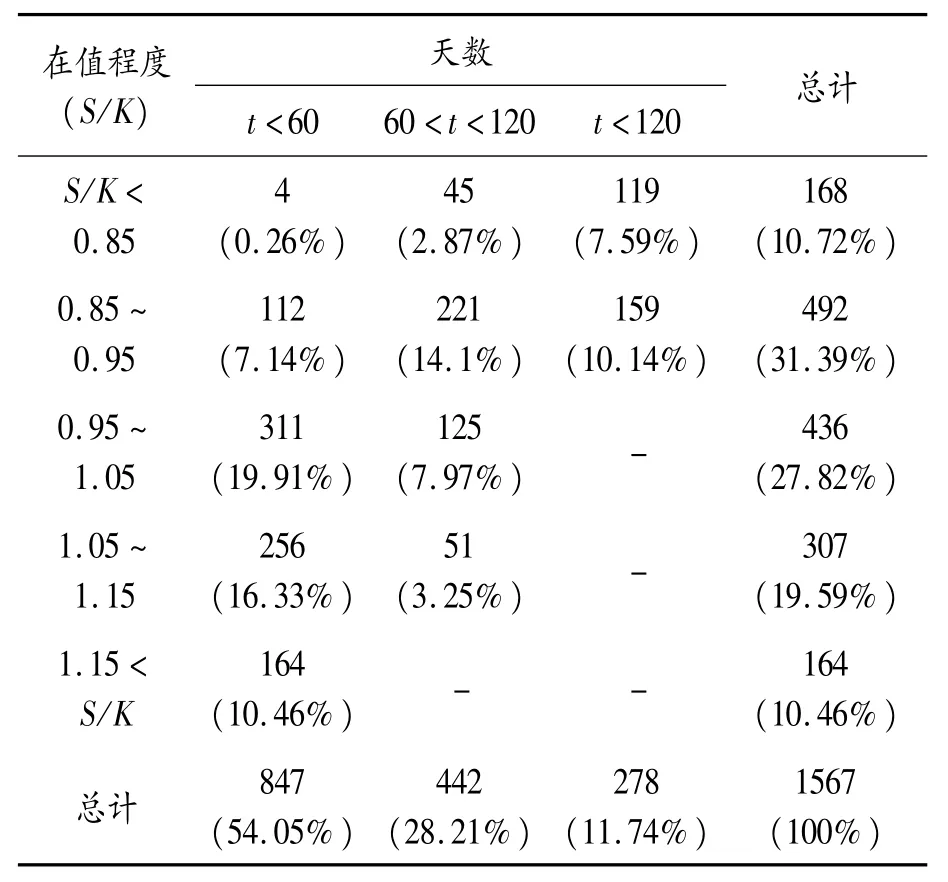
表2 上证50ETF期权数据

表3 标准均方根误差

4 结束语

本文将混合正态异方差模型应用到期权定价中，提供了在一般框架下的资产收益以及如何获得适当的风险中性状态下的资产收益的方法。此外，在贝叶斯框架中进行参数估计，使我们能够在考虑了参数的不确定性的情况下计算出预测的价格密度，从而推导出期权定价。实证结果表明：该模型对收益率数据可以进行有效的统计分析，预测出的期权价格与实际情况相比效果也比较好，值得进一步深入研究和推广。