一种基于几何约束的插值曲线的参数连续性
师 晶
(闽南理工学院 信息管理学院, 福建 石狮 362700)
计算机辅助几何设计的主要功能是用来满足工业中曲线曲面的几何造型要求.随着工业产品设计的复杂化、几何形状要求的多样化,原有的传统曲线曲面无法方便地、灵活地描述一些造型复杂的曲线曲面.这时,通常采用组合曲线曲面解决这些问题,因此,CAGD引入了曲线曲面的拼接问题.
在CAGD中,Bezier曲线与B样条曲线是两种主要的曲线构造方法[1-3].它们具有许多良好的性质,如结构简单、使用方便等.然而,Bezier曲线的形状是由控制顶点唯一确定的,若要改变Bezier曲线的形状,必须调整相应的控制顶点.此外,Bezier方法与B样条方法既不能描述除抛物线以外的圆锥曲线,也不能精确描述工程中常见的二次曲面,这为曲线曲面造型带来一定的不便.近年来,人们对三角函数空间中构造的曲线进行了很多研究,但此类曲线仍存在局部调控不灵活等问题[4-5].
本文研究一种基于几何约束的插值曲线的参数连续性.这种插值曲线不仅具有类似样条曲线的一些性质,如端点插值性、凸包性、保凸性和形状可调性等,而且在曲线间C1,C2的光滑拼接条件下,通过调整形状参数,还可较好地设计一些曲线曲面.
1 基础知识
给定R2中的两端点Pi(i=1,2),两端点处的两条切线Li(i=1,2)以及两个实常数Ki(i=1,2).现构造一条插值曲线G(λ),使其依次通过两端点,并且在两端点Pi(i=1,2)处的切线分别为Li(i=1,2),曲率分别是Ki(i=1,2).设L3是通过P1,P2两点的直线,点P3是直线L1,L2的交点.直线Li(i=1,2,3)的方程为
li(x,y)=aix+biy+ci,i=1,2,3.
(1)

通过点P1并且在点P1的切线为L1的圆的标准化方程为
φ(x,y)=(x-m)2+(y-n)2-R2,
(2)
其中R是圆φ(x,y)=0的半径.
假设K1≠0,K2=0,插值两端点两切线两曲率的曲线G(λ)定义为
(3)
其中0<λ<1为形状参数,如图1所示.
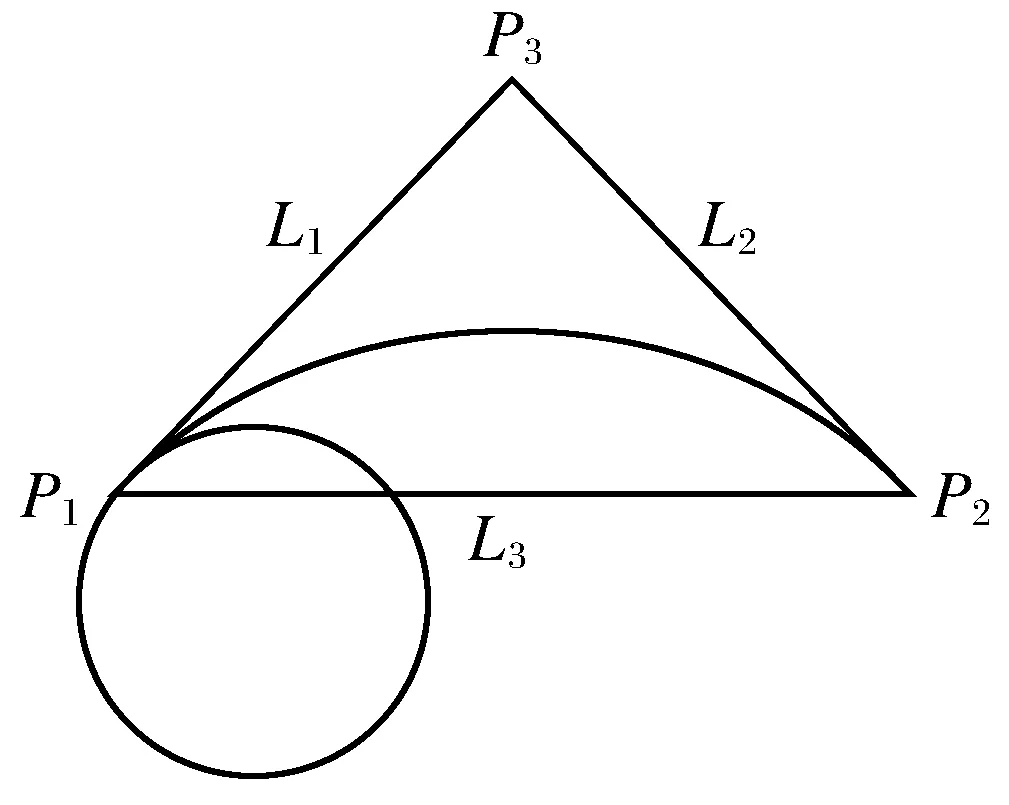
图1 插值曲线Fig.1 The interpolation curve
引理1 设G:g(x,y)=0是R2中的代数曲线,其中g(x,y)是关于x,y的至少一阶连续偏导数,P(x,y)是G上的正则点,那么曲线G在点P(x,y)的切向量为Δg(x,y)={gy,gx}(x,y).
引理2 曲线G(λ)在两端点P1,P2处的切向量分别为如下形式:
(4)
证明 由式(1)~式(3)得曲线G(λ)的一阶偏导数
由于圆φ(x,y)=0和直线L3的交点是P1,直线L2,L3的交点是P2,故
φ(P1)=0,l3(P1)=0,l2(P2)=0,l3(P2)=0,
代入上式得
根据引理1化简可得曲线G(λ)在两端点P1,P2处的切向量为式(4).
引理3 曲线G(λ)在两端点P1,P2处的二阶偏导数分别为如下形式:
(5)
证明 由引理2得曲线G(λ)的二阶偏导数
因为φ(P1)=0,l3(P1)=0,l2(P2)=0,l3(P2)=0,分别代入上式化简可得曲线G(λ)在两端点P1,P2处的二阶偏导数为式(5).
定义1 设G:g(x,y)=0是区间[a,b]内的代数曲线,在区间[a,b]内取n-1个分点,它们依次为a=x0 [a,b]=[x0,x1]∪[x1,x2]∪…∪[xn-1,xn], 其中xi(i=1,2,…,n-1)表示曲线中拐点、尖点或极值点的横坐标.在区间(xi-1,xi)中,第i段曲线表示为 Gi:gi(x,y)=0,x∈(xi-1,xi). (1) 端点性质:该曲线插值于首、末两端点,并且与控制△P1P2P3的两边相切,即 证明 由式(4)和式(5),曲线G(λ)在端点P1处与端点P2处曲率分别是 (3) 凸包性和保凸性:设圆φ(x,y)=0与直线L3的另一个交点是A,则当λ>0且点A在P1P2线段的延长线上时,曲线G(λ)在控制△P1P2P3内保凸. 证明 ① 存在性.由题意得,当A位于线段P1P2的延长线上时,除去P1,P2,对线段L3上任一点P4有 φ(P4)<0,l2(P4)>0,l3(P4)=0, 故g(P4)=g(P4)l2(P4)<0. ② 凸包性和保凸性.在控制△P1P2P3中任意作一直线L,设其与直线L1,L2分别交于点Q1,Q2,由题意得, 由于g(Q1)与g(Q2)同号,所以直线L与曲线G(λ)在△P1P2P3内的交点个数为偶数.而G(λ)是三次曲线,所以交点个数是0个或2个,故当A不在P1、P2所在的线段上且λ>0时,G(λ)在控制△P1P2P3内的曲线是凸的. 综上所述,当λ>0且点A在P1P2线段的延长线上时,曲线G(λ)在控制△P1P2P3内保凸,如图2所示. (4) 几何不变性:曲线G(λ)的形状取决于R2中的两点Pi(i=1,2),两条切线Li(i=1,2)以及两个实常数Ki(i=1,2),与坐标系的位置无关. (5) 形状可调性:固定两端点Pi(i=1,2),两端点处的两条切线Li(i=1,2)以及两个实常数Ki(i=1,2),当形状参数λ逐渐增大(或减小)时,曲线G(λ)在控制△P1P2P3内逐渐远离(或靠近)控制顶点P3,可通过改变参数的大小调控曲线的形状,如图3所示. 图2 当λ>0时,点A位于不同位置时G(λ)的图形Fig.2 Graphs of G(λ) when point A is in different positions with λ>0(a)—点A位于线段P1P2上; (b)—点A与P2重合; (c)—点A位于线段P1P2的延长线上. 图3 曲线G(λ)中不同参数的取值 (6) 定理1 两曲线G1(λ1)和G2(λ2)的C1连续的充要条件如下. (1) 若P12=P21是两曲线G1(λ1)和G2(λ2)的公共连接点,则这两条曲线在P12=P21处C1连续的充要条件是 (7) (2) 若P12=P22是两曲线G1(λ1)和G2(λ2)的公共连接点,则这两条曲线在P12=P22处C1连续的充要条件是 (8) (3) 若P11=P21是两曲线G1(λ1)和G2(λ2)的公共连接点,则这两条曲线在P11=P21处C1连续的充要条件是 (9) 证明 (1)因为P12=P21是两曲线G2(λ1)和G2(λ2)的公共连接点,所以这两条曲线是C0连续的.两曲线G1(λ1)和G2(λ2)在P12=P21处C1连续,还应满足它们在公共连接点处具有相同的一阶导数,即 (10) 此时直线L12与L21重合,即l12=l21. 由引理2及式(6)得 将上式代入式(10)化简得 所以式(7)是两曲线G1(λ1)和G2(λ2)在公共连接点P12=P21处C1连续的充要条件. 类似地可以证明定理1中的(2)和(3). 两曲线G1(λ1)和G2(λ2)的C1连续的几何意义是:P13,P23和公共连接点三点共线,且点P13和P23位于公共连接点两侧. 定理2 两曲线G1(λ1)和G2(λ2)的C2连续的充要条件如下. (1) 两曲线G1(λ1)和G2(λ2)在公共连接点P12=P21处C2连续的充要条件是满足式(7)及 (11) (2) 两曲线G1(λ1)和G2(λ2)在公共连接点P12=P22处C2连续的充要条件是满足式(8)及 (3) 两曲线G1(λ1)和G2(λ2)在公共连接点P11=P21处C2连续的充要条件是满足式(9)及 证明 (1) 两曲线G1(λ1)和G2(λ2)在公共连接点P12=P21处C2连续的充要条件是:除满足C0,C1连续条件外,还应满足它们在公共连接点处具有相同的二阶导数,即 (12) 由引理3及式(6)得 将上式代入式(12)化简得 所以式(7)和式(11)是两曲线G1(λ1)和G2(λ2)在公共连接点P12=P21处C2连续的充要条件. 类似地可以证明定理2中的(2)和(3). 两曲线G1(λ1)和G2(λ2)的C2连续的几何意义是:控制三角形△P11P12P13和△P21P22P23共面. 利用插值曲线的拼接定理及良好的形状可调性,可方便地构造一些常用曲线曲面图形,具体拼接步骤如下: 步骤1 给定代数曲线G,根据定义1的方法对代数曲线G进行分段,得到曲线段Gi(i=1,2,…,n),Gi在区间(xi-1,xi)内具有固定的凹凸性和单调性; 步骤2 根据曲线段Gi的两端点、两切线及曲率,计算出插值曲线Gi(λ)[6-8]; 步骤3 绘制插值曲线Gi(λ),并通过修改λ的值调节曲线形状; 步骤4 根据定理1、2对插值曲线Gi(λ)依次进行光滑拼接. 插值两端点两切线两曲率的曲线G(λ)本身具有形状控制参数,可以通过选取不同的参数值来调整同一控制三角形中曲线的形状,并且通过曲线间的连续条件,可以方便地把曲线G(λ)应用到曲线曲面造型中. 梨曲线图形是由多条插值曲线G(λ)拼接而成的.在控制三角形△P11P12P13和△P21P22P23中,当两个形状参数λ1,λ2分别取7,0.9时,拼接而成的曲线如图4所示.同理可得梨曲线图形的其他部分,根据曲线间的连续条件,将曲线段分别按定理1和定理2进行拼接,得到的梨曲线图形如图5所示. 图4 部分梨曲线的控制三角形Fig.4 The control triangles for some pear curves 图5 插值曲线拼接的梨曲线Fig.5 Pear curves joined by interpolation curves 图6所示酒杯旋转曲面的母线是由两条插值曲线G(λ)拼接而成的, 从图6中可以看出, 两条曲线段在公共连接点处具有较好的拼接效果. 图7是插值曲线G(λ)生成的酒杯旋转曲面. 图6 酒杯旋转曲面的母线Fig.6 The generatrix of the wine glass rotating surface 图7 酒杯旋转曲面Fig.7 Wine glass rotating surface 本文通过研究一种基于几何约束的插值曲线的端点性质、凸包性和保凸性等,给出两条插值曲线的C1,C2连续条件及几何意义.这种插值曲线在控制三角形中,可通过选取不同的参数值来调整曲线的形状,具有较好的形状可调性.实例表明,该插值曲线的连续性条件可较好地构造一些曲线曲面图形,这对于计算机辅助几何设计具有一定的实用价值.2 曲线性质
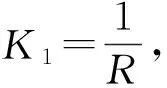


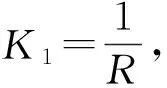
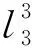
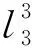
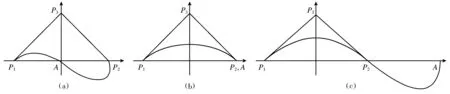

3 曲线拼接
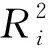

4 拼接步骤
5 计算实例




6 结 语

