考虑潮位变动的淹没水平板防波堤设置方案

高喜峰，王洪树，贺 铭，徐万海



考虑潮位变动的淹没水平板防波堤设置方案

高喜峰，王洪树，贺 铭，徐万海

(天津大学水利工程仿真与安全国家重点实验室，天津 300350)

淹没水平板借助上部波浪破碎、端部涡旋脱落、底部脉动回流等机理能够较好地抵御波浪入侵，是一种富有开发价值的透空型防波堤．然而淹没水平板多采用桩柱支撑，结构高程不随潮位的变化而改变．在潮差较大的海域，低潮位时水平板可能位于水面以上，而高潮位时其浸没深度又可能过大，两种情况下水平板防波堤均不能有效抵御波浪．为此，本文探讨如何设置双层水平板防波堤来削弱潮位变动对消浪性能的不利影响．研究基于光滑粒子流体动力学(SPH)方法进行，首先建立了模拟波浪与淹没水平板相互作用的二维数值波浪水槽，接着以文献中记录的物理模型实验为目标，重现了孤立波和规则波与单层淹没水平板的相互作用过程．数值计算得到的波面形态、结构波浪力、基倍频波浪透射系数均与实测结果吻合较好．随后应用验证过的数学模型，对单层水平板和两种形式的双层水平板的消浪性能进行了比较．一方面展现出在变潮位环境下采用双层水平板的必要性，另一方面从所提出的两种双层水平板设置方案中确定出较优的形式．进一步地，综合对波浪透射系数和水平板垂向波浪力的分析，得出双层水平板防波堤的最佳板间距．研究结果表明，在高低潮位下各设置一层水平板所组合而成的双层水平板防波堤能够有效克服潮位变动对消浪性能的不利影响，且双层水平板的最佳板间距宜与潮差相等．

淹没水平板；潮位；波浪透射系数；波浪力；薄壁结构；光滑粒子流体动力学

防波堤是抵御波浪入侵、掩护港湾内船舶作业的工程结构．在其众多形式中，淹没水平板防波堤以其对地质条件要求较低、深水环境下性价比较高、不阻断掩护区内外水质交换等优点，受到科研界和工程界的共同关注．

早期开展的淹没水平板水动力性能研究多采用解析方法．如Heins[1]使用Wiener-Hopf方法推导了有限水深半无限水平板的波浪透反射解析解．Siew等[2]利用匹配渐近展开法分析了淹没水平板对浅水长波的散射作用．Cho等[3]和Liu等[4]分别采用特征函数展开法研究了波浪与弹性板及开孔板间的相互作用．Dong等[5]近期推导了不平整海底地形条件上波浪与单层刚性水平板相互作用的解析解．

解析研究提升了对淹没水平板水动力性能的认识，但通常受线性或弱非线性假设的局限．而为获得较好的消浪性能，淹没水平板需靠近自由液面[6]，水平板上部波浪非线性较强．为此，Liu等[7-8]基于去奇异边界积分方程法建立了一套完全时域非线性数值波浪水槽，用以研究波浪在固定和弹性支撑水平板上的非线性传播过程．Lalli等[9]分别利用线性和非线性边界元方法计算了波浪与淹没水平板的相互作用过程，比较发现基于线性假定无法完整地给出透射波浪的信息．

由于水平板端部存在剧烈的涡旋场[10]，因此关于淹没水平板的数值计算还应考虑流体黏性作用．随着计算流体力学的发展和计算机运算能力的提升，基于求解黏性流体控制方程的仿真模拟得以实现．如Jin等[11]建立了波浪与淹没水平板相互作用的有限体积模型，其中使用-模型描述流体湍流运动，使用流体体积函数(VOF)方法捕捉自由液面．Qi等[12]利用有限差分法离散雷诺平均Navier-Stokes方程，模拟了水平板顶部波浪破碎、尾部涡脱落和底部脉动回流等现象．

除上述数值研究工作外，现也开展了大量关于淹没水平板水动力性能的物理模型实验研究．Patarapanich等[13]测试并找到了规则波和不规则波作用下单层淹没水平板的最佳浸没深度和板长．Gu等[14-15]测量了多向不规则波作用下双层水平板的消浪性能和波浪力情况．Fang等[16]探讨了4层开孔水平板的优化布置问题．

现有淹没水平板研究仍存在的一个不足是多假定水位固定不动，与真实海洋环境中潮位时刻变化的情况不相符．传统有网格数值方法在处理结构出入水问题时需依赖复杂算法来捕捉流-固-气交界面，且需耗费大量的时间和资源来调整或重新划分网格．而以光滑粒子流体动力学(SPH)为代表的新兴无网格方法则极其方便．SPH方法将物质材料用离散分布的节点来表示，且各节点间没有固定的几何拓扑关系，因此在模拟流固体大变形和复杂自由液面问题上优势显著[17-19]．近年来，该方法被广泛应用在流固耦合问题的数值计算上，取得大量成功先例[20-25]．

采用SPH方法研究淹没水平板问题的主要难点在于对水平板薄壁特性的模拟．由于SPH粒子间没有固定几何拓扑关系，水平板上下两侧本无接触的流体粒子间将发生非物理性相互作用．为此，Meringolo等[26]提出了多节点固定虚粒子方法，实现了以低一级空间分辨率对相同厚度薄壁结构的模拟．Ren等[27]发明了模拟零厚度结构的色域粒子技术．

本文将Meringolo等[26]的思想融入到动力学固边界处理方法中，提出了多层动力学边界粒子法，在相同的空间分辨率情况下，比Meringolo等[26]所模拟的薄壁结构厚度更薄．基于该种薄壁结构处理方法，建立了波浪与淹没水平板相互作用的二维弱可压缩SPH模型，并用于研究考虑潮位变动情况下的淹没水平板防波堤的设置问题．

1 数学模型

1.1 流体控制方程

SPH方法的基本理论和推导公式可参见文献[28]，这里直接给出经SPH方法离散后的弱可压缩黏性流体运动控制方程．

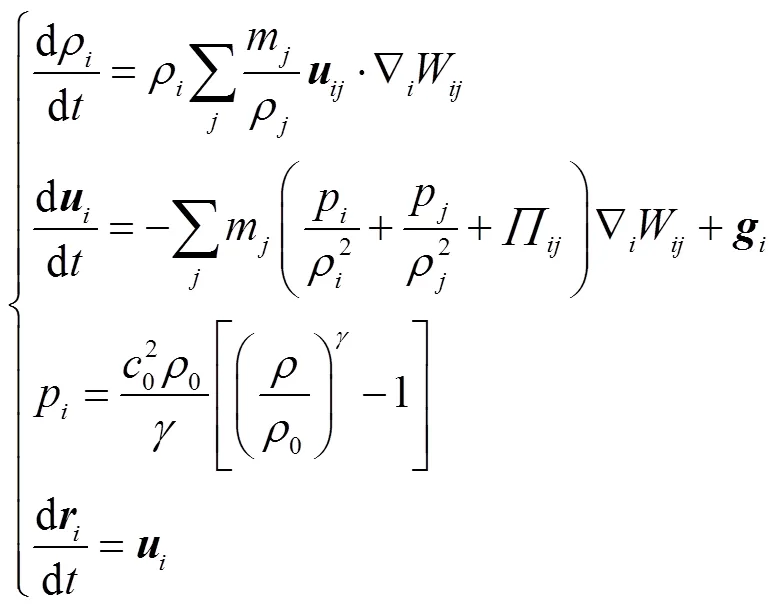
由于弱可压缩SPH的密度场存在高频振荡，因此利用简单的Shepard密度过滤法来稳定数值计算，即每30个计算步应用式(2)重新指定流体粒子的 密度．

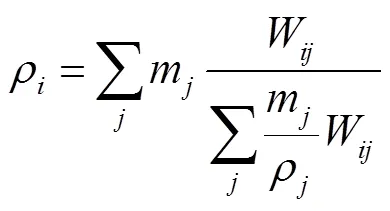
1.2 数值积分

采用具有二阶精度的预报校正法[29]求解式(1).另外为保证数值积分的稳定性，选用了由式(3)计算得到的可变时间步长．

式中：等号右侧的3项依次为CFL条件、黏性扩散项和粒子加速度项；0是流体的运动学黏度．

1.3 固壁边界条件

1.3.1 一般固壁边界

一般固壁边界(包括数值波浪水槽的侧壁和底边壁)由动力学边界粒子方法[30]实施．具体地，在固壁边界上设置两排固壁粒子，其与流体粒子一样参与连续性方程和状态方程的计算，但位置和速度不随时间改变，或按照指定速度人为施加(指造波板上的固壁粒子)．采用传统的动力学边界粒子法处理干湿交界面时，面临密度场梯度异常和粒子间非物理性吸附或排斥等问题，为此需用式(4)来修正固壁粒子的密度．

(4)

1.3.2 薄壁边界

由于水平板的水平尺度远大于其厚度，因此可视其为薄壁结构，则在布置固壁粒子时希望所用排数尽可能少．如果使用第1.3.1节中的动力学边界粒子方法，则至少需布置4排固壁粒子，否则水平板底侧(顶侧)的流体粒子会通过改变固壁粒子的密度来间接作用于顶侧(底侧)的流体粒子．也就是说，结构的最小厚度为4p．

图1 多层动力学边界粒子示意

1.3.3 流体力计算

基于流体粒子和固壁粒子间的动量方程，得到流体粒子对固壁粒子的作用力．

(5)

将水平板上全部固壁粒子(共3层)受到的作用力累加，得到水平板所受总流体力为

(6)

式(6)包含静水压力和动水压力2部分．对于如淹没水平板一类位于静水位以下的结构，垂向静水压力等于结构浮力，则垂向动水压力计算式为

(7)

式中为水平板的长度．

2 模型验证

2.1 孤立波与淹没水平板相互作用

图2 孤立波与淹没水平板相互作用示意(单位：m)

图3 计算与实测波面形态的比较

图4 计算与实测垂向波浪力的比较

2.2 规则波与淹没水平板相互作用

(8)

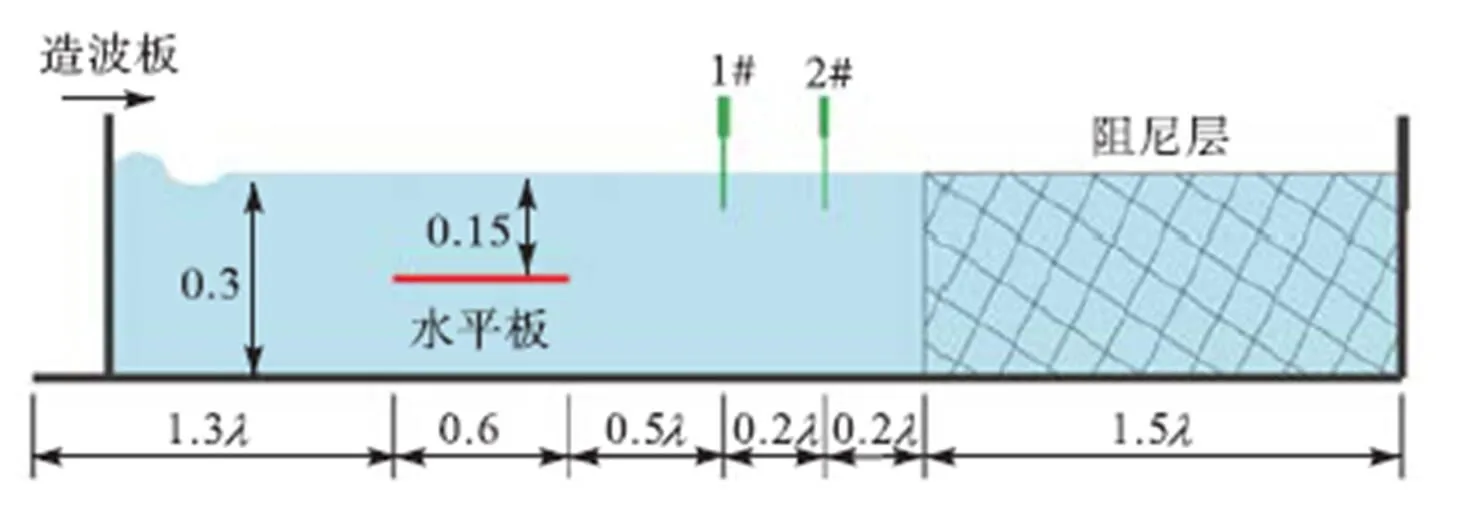
图5 规则波与淹没水平板相互作用示意(单位：m)

图6 计算与实测波浪透射系数的比较

3 结果与讨论

3.1 计算设置

我国沿海潮差介于0.7～5.5m之间[35]，跨越弱、中、强3个潮差区间．在强潮区宜建造高度可调节的防波堤(如浮式防波堤)来抵御波浪，而在弱潮区使用单层淹没水平板即可取得较好的消浪效果，以上两种情况均非本次研究所要探讨的．本次研究关注的是中等潮差海域(潮差介于2～4m)淹没水平板的二维设置问题．潮差D设为3m，低潮位水深＝8m，板长与波长比值/介于0.25～0.85区间，波高选取1m和2m两种．

3.2 结果与分析

为兼顾淹没水平板在高、低潮位下的消浪性能，水平板应设置在低潮位以下．研究[13]表明，当水平板浸没深度与水深比p/介于0.05～0.15区间时其消浪性能最佳，但考虑尽可能减小高潮位时水平板的浸没深度，低潮位时p/取为0.05．

图7为高、低潮位下单层水平板的基频波浪透射系数的比较．可以看到，低潮位下单层水平板的消浪性能良好，T基本控制在0.4以下，特别是当＝2m、/＝0.55时T尚不足0.1．但高潮位下T显著增大，虽然当/≈0.32时，T小于0.5，但鉴于海洋波浪的随机性，认为在中等潮差海域单层淹没水平板消浪性能不佳．

使用双层水平板是克服潮位变动不利影响的一种解决方案，但现有研究多探讨固定水位下双层水平板的设置问题，很少有结合潮位变动开展的双层板布置研究．本文对图8所示的两种双层板系统进行了研究：方案1为2#水平板设置在低潮位与高潮位之间；方案2为2#水平板设置在1#水平板底部．

低潮位下，方案1中2#水平板位于静水位以上，因此对波浪传播的影响较小，双层板系统的消浪性能与单层板接近．方案2中波浪主要与浸没深度较小的1#水平板相互作用，因此双层板系统的消浪性能主要受1#板控制．

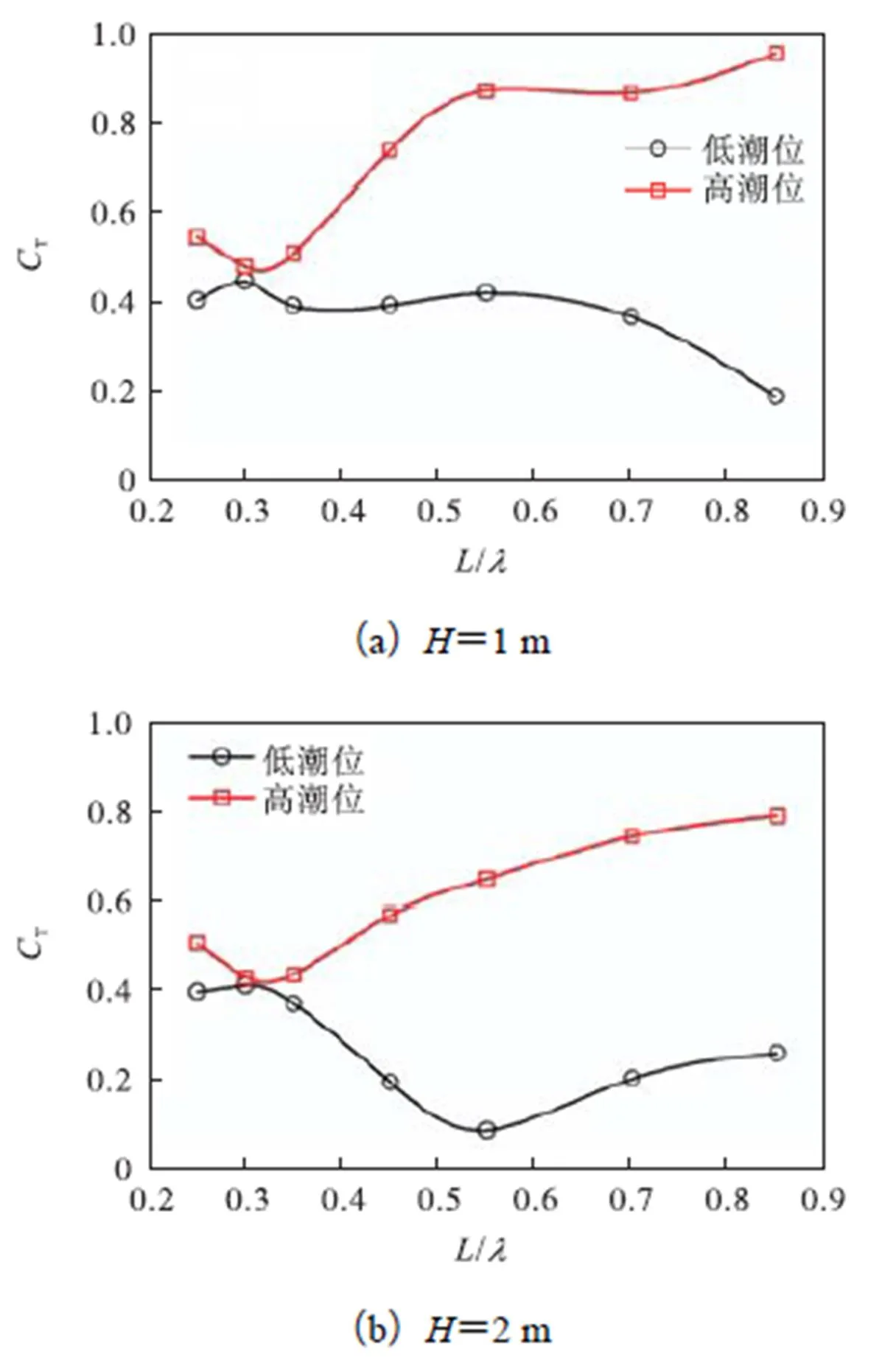
图7 高、低潮位下单层水平板CT的比较

图8 双层水平板系统的两种设置方案

图10给出高潮位下单层水平板与第2种双层水平板T的比较．可以看到，在1#水平板下部增设2#水平板，虽然也能够提升消浪性能，但效果远不如第1种双层板方案，并且无法判断*设置为多少更合适．不过在高潮位下，第1种双层板方案会因2#水平板露出水面而影响岸线景观．

图9 高潮位下单层板与第1种双层板CT的比较

图10 高潮位下单层板与第2种双层板CT的比较

图11～14为高潮位下/＝0.55时单、双层水平板周围的流体压力和速度分布情况的比较．结果以一个波浪周期内的4个典型时刻(＝0，0＋0.25，0＋0.50，0＋0.75)给出，其中0为波峰到达水平板迎浪端的瞬时．速度矢量标记在结构化网格的节点上，速度大小和方向通过对节点周围拉格朗日粒子信息的插值得到．

图11 t＝t0时单层板与双层板周围压力场和速度场的比较

图12 t＝t0+0.25T时单层板与双层板周围压力场和速度场的比较

图13 t＝t0+0.50T时单层板与双层板周围压力场和速度场的比较

图14 t＝t0+0.75T时单层板与双层板周围压力场和速度场的比较

比较单层板和第1种双层板发现，波浪经过单层板时，在浅水效应的作用下波面非线性增大，有微弱的溢破现象产生，伴随有少量波能损耗．而2#水平板的存在极大地减小了防波堤系统的浸没深度，导致浅水波浪崩破，波能大量损耗并由基频波浪向高倍频波浪转化．另外，双层板背浪侧产生了明显的涡旋流场，涡的内摩擦也极大地消耗了入射波能．综上两方面因素，第1种双层板的消浪性能显著优于单层板．

比较单层板和第2种双层板发现，2#水平板的存在主要增大了防波堤系统的迎浪面积，继而增强了波浪的反射作用．但由于2#水平板设置在1#水平板底部，其对浅水波浪形态的影响可忽略不计，因此不会过多贡献额外的波浪破碎耗能．另外，同单层板一样，第2种双层板背浪侧也观察不到无明显的涡旋流场，亦就不会因涡内摩擦损耗波能．因此，第2种双层板的消浪性能略好于单层板．

图15进一步给出第1种双层水平板波浪力随板间距的变化结果．对于桩锚系统，最不利荷载为波浪力向上且达到最大值的情况，因此图15中的波浪力结果以最大向上波浪力的无因次化形式Z*/呈现．可以看到，Z*/随板间距的增大而显著减小．当＝1m且/＞0.65时，双层板甚至仅受向下波浪力的作用．综合图9对波浪透射系数和图15对垂向波浪力的研究结果，可认为板间距s＝1.0的第1种双层水平板方案最佳．

图15 高潮位下不同间距的双层板波浪力的比较

4 结 论

本次研究建立了波浪与淹没水平板相互作用的二维SPH数学模型．通过与物理模型实验的比较，验证了所建立数学模型的可靠性．以此研究了潮位变化对单层淹没水平板消浪性能的影响，分析了双层水平板在潮位变动情况下的消浪性能，并从消浪性能和波浪力两个角度对双层板的垂向间距进行了优化．结果表明：

(1) 在中等潮差海域，单层淹没水平板防波堤的消浪能力不足；

(2) 在高低潮位下各设置一层水平板所形成的双层板系统能够克服潮位变动对水平板防波堤消浪性能的不利影响；

(3) 双层水平板的垂向间距建议设置为潮差的高度．

需要说明的是，本文工作是在规则波浪简化条件下进行的，所得到的结论仍有局限性．但目前基于SPH方法的不规则波浪生成技术[36]和波流耦合方 法[37]已基本实现，有望近期引入至淹没水平板水动力分析中，以使研究结果更具实践价值．

［1］ Heins A E. Water waves over a channel of finite depth with a submerged plane barrier[J]. Canadian Journal of Mathematics，1950，2：210-222.

［2］ Siew P F，Hurley D G. Long surface waves incident on a submerged horizontal plate[J]. Journal of Fluid Mechanics，1977，83(1)：141-151.

［3］ Cho I H，Kim M H. Interactions of a horizontal flexible membrane with oblique incident waves[J]. Journal of Fluid Mechanics，1998，367：139-161.

［4］ Liu Y，Li YC. An alternative analytical solution for water-wave motion over a submerged horizontal porous plate[J]. Journal of Engineering Mathematics，2011，69(4)：385-400.

［5］ Dong J，Wang B，Zhao X，et al. Wave forces exerted on a submerged horizontal plate over an uneven bottom[J]. Journal of Engineering Mechanics，2018，144(6)：04018030.

［6］ Verduzco-Zapata M G，Ocampo-Torres F J，Mendoza E，et al. Optimal submergence of horizontal plates for maximum wave energy dissipation[J]. Ocean Engineering，2017，142：78-86.

［7］ Liu C，Huang Z，Chen W. A numerical study of a submerged horizontal heaving plate as a breakwater[J]. Journal of Coastal Research，2017，33(4)：917-930.

［8］ Liu C，Huang Z，Tan S K. Nonlinear scattering of non-breaking waves by a submerged horizontal plate：Experiments and simulations[J]. Ocean Engineering，2009，36(17/18)：1332-1345.

［9］ Lalli F，Bruschi A，Liberti L，et al. Analysis of linear and nonlinear features of a flat plate breakwater with the boundary element method[J]. Journal of Fluids and Structures，2012，32：146-158.

［10］ Poupardin A，Perret G，Pinon G，et al. Vortex kinematic around a submerged plate under water waves. Part I：Experimental analysis[J]. European Journal of Mechanics B/Fluids，2012，34：47-55.

［11］ Jin H，Liu Y，He S-Y，et al. Numerical study on the wave dissipating performance of a submerged horizontal plate breakwater using OpenFOAM[C]// Proceedings of the Eleventh(2014)Pacific/Asia Offshore Mechanics Symposium. Shanghai，China，2014：307-311.

［12］ Qi P，Hou Y-J. Numerical wave flume study on wave motion around submerged plates[J]. China Ocean Engineering，2003，17(3)：397-406.

［13］ Patarapanich M，Cheong HF. Reflection and transmission characteristics of regular and random waves from a submerged horizontal plate[J]. Coastal Engineer-ing，1989，13(2)：161-182.

［14］ Gu Q，Huang G，Zhang N，et al. Experimental study on the wave loads of twin-plate breakwater under oblique waves[J]. Acta Oceanologica Sinica，2016，35(12)：100-109.

［15］ Gu Q，Huang G，Zhang N，et al. Wave-dissipating performance of twin-plate breakwater under oblique random waves[J]. International Journal of Offshore and Polar Engineering，2017，27(2)：184-192.

［16］ Fang Z，Xiao L，Kou Y，et al. Experimental study of the wave-dissipating performance of a four-layer horizontal porous-plate breakwater[J]. Ocean Engineering，2018，151：222-233.

［17］ Ming F R，Sun P N，Zhang A M. Numerical investigation of rising bubbles bursting at a free surface through a multiphase SPH model[J]. Meccanica，2017，52(11)：2665-2684.

［18］ Khayyer A，Gotoh H. On particle-based simulation of a dam break over a wet bed[J]. Journal of Hydraulic Research，2010，48(2)：238-249.

［19］ Khayyer A，Gotoh H，Shao S. Corrected incompressible SPH method for accurate water-surface tracking in breaking waves[J]. Coastal Engineering，2008，55(3)：236-250.

［20］ Ming F R，Zhang A M，Xue Y Z，et al. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions[J]. Ocean Engineering，2016，117：359-382.

［21］ Ren B，He M，Li Y，et al. Application of smoothed particle hydrodynamics for modeling the wave-moored floating breakwater interaction[J]. Applied Ocean Research，2017，67：277-290.

［22］ Zheng X，Lü X，Ma Q，et al. An improved solid boundary treatment for wave-float interactions using ISPH method[J]. International Journal of Naval Architecture and Ocean Engineering，2018，10(3)：329-347.

［23］ Gao X，He M，Xu W，et al. Hydroelastic analysis of a submerged horizontal plate using a coupled SPH-FEM model[C]// Proceedings of the ASME 2018 37th International Conference on Ocean，Offshore and Arctic Engineering. Madrid，Spain，2018.

［24］ Li Y，He M，Ren B，et al. Numerical simulation of wave interaction with a hinged multi-module floating structure[C]// Proceedings of the ASME 2017 36th International Conference on Ocean，Offshore and Arctic Engineering. Trondheim，Norway，2017.

［25］ Shi Y，Li S，Chen H，et al. Improved SPH simulation of spilled oil contained by flexible floating boom under wave-current coupling condition[J]. Journal of Fluids and Structures，2018，76：272-300.

［26］ Meringolo D D，Aristodemo F，Veltri P. SPH numerical modeling of wave-perforated breakwater interaction[J]. Coastal Engineering，2015，101：48-68.

［27］ Ren X-F，Sun Z-C，Wang X-G，et al. SPH numerical modeling for the wave-thin structure interaction[J]. China Ocean Engineering，2018，32(2)：157-168.

［28］ Zhang AM，Sun PN，Ming FR，et al. Smoothed particle hydrodynamics and its applications in fluid-structure interactions[J]. Journal of Hydrodynamics，2017，29(2)：187-216.

［29］ Monaghan J J. Simulating free surface flows with SPH[J]. Journal of Computational Physics，1994，110(2)：399-406.

［30］ Ren B，He M，Dong P，et al. Nonlinear simulations of wave-induced motions of a freely floating body using WCSPH method[J]. Applied Ocean Research，2015，50：1-12.

［31］ Lo HY，Liu P LF. Solitary waves incident on a submerged horizontal plate[J]. Journal of Waterway，Port，Coastal，and Ocean Engineering，2014，140(3)：04014009.

［32］ Goring D G. Tsunamis：The propagation of long waves onto a shelf[D]. Pasadena，California：Division of Engineering and Applied Science，California Institute of Technology，1978.

［33］ Hirakuchi H，Kajima R，Kawaguchi T. Application of a piston-type absorbing wavemaker to irregular wave experiments[J]. Coastal Engineering in Japan，1990，33(1)：11-24.

［34］ Grue J. Nonlinear water waves at a submerged obstacle or bottom topography[J]. Journal of Fluid Mechanics，1992，244：455-476.

［35］ 胡方西，谷国传. 中国沿岸海域月平均潮差变化规律[J]. 海洋与湖沼，1989，20(5)：401-411.

Hu Fangxi，Gu Guochuan. Seasonal changes of the mean tidal range along the Chinese coasts[J]. Oceanologia et Limnologia Sinica，1989，20(5)：401-411(in Chinese).

［36］ Wen H，Ren B. A non-reflective spectral wave maker for SPH modeling of nonlinear wave motion[J]. Wave Motion，2018，79：112-128.

［37］ He M，Gao XF，Xu WH. Numerical simulation of wave-current interaction using the SPH method[J]. Journal of Hydrodynamics，2018，30(3)：535-538.

Configuration of Submerged Horizontal Plate Breakwater Considering Tidal-Level Variation

Gao Xifeng，Wang Hongshu，He Ming，Xu Wanhai

(Stake Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300350，China)

On the help of the wave breaking above，the vortex shedding at the ends，and the pulsating flow beneath，a submerged horizontal plate attenuates incident water waves passing over the plate and becomes an exploitable open-type breakwater. However，restrained by piles，the elevation of the plate remains unchanged during tidal-level fluctuations. In case of a large tidal range, the plate may be exposed above the low-tidal water surface，but at high tide，the submergence of the plate can be large. Both situations are unfavorable for the wave attenuation performance of the submerged horizontal plate breakwater. In this regard，the method of designing a twin-plate system to weaken the adverse effect of tidal-level variation is discussed. Based on the smoothed particle hydrodynamics (SPH) method, a 2D numerical wave tank (NWT) was first built. Following available experiments in the literature，the NWT was used to reproduce solitary wave as well as regular wave interaction with single submerged horizontal plates. The wave profiles，wave forces，and fundamental- and high-order wave transmission coefficients obtained by numerical calculation agree well with the measured results. The validated SPH model was applied to compare the wave transmission coefficients between a single-plate and two twin-plate systems with different configurations. The necessity of using a twin-plate system in the tidal-level varying environment was confirmed. Additionally，the superior configuration out of the two proposed twin-plate systems was determined. Furthermore，the optimal spacing between the twin-plates was determined by comprehensive analysis of the wave transmission coefficient and vertical wave force. The results indicate that a twin-plate system with one plate below the low water level and the other between the low and high water levels can effectively cope with the tidal-level variation. The vertical spacing between the twin-plates is recommended to be equal to the tidal range.

submerged horizontal plate；tidal-level；wave transmission coefficient；wave force；thin-wall structure；smoothed particle hydrodynamics(SPH)

10.11784/tdxbz201806015

TV139.2

A

0493-2137(2019)05-0529-10

2018-07-05；

2018-09-20.

王树新（1966— ），男，博士，教授.

张国凯，zhang_gk@tju.edu.cn.

国家自然科学基金资助项目(51475323)；国家重点研发计划资助项目(2017YFC0110403).

the National Natural Science Foundation of China(No. 51475323)，the National Key Research and Development Program of China(No. 2017YFC0110403).

(责任编辑：王新英)