基于预测控制的无人驾驶车辆爆胎转向控制
胡超芳,曹 磊,赵凌雪,王 娜
基于预测控制的无人驾驶车辆爆胎转向控制
胡超芳1, 2, 3,曹 磊1, 2, 3,赵凌雪1, 2, 3,王 娜3, 4
(1. 天津大学电气自动化与信息工程学院,天津 300072; 2. 系统控制与信息处理教育部重点实验室,上海 200240; 3. 微光机电系统技术教育部重点实验室(天津大学),天津 300072; 4. 天津工业大学电气工程与自动化学院,天津 300387)
针对无人驾驶车辆爆胎后的转向控制问题,考虑实时性和控制性能的要求,提出了连续时域自适应预测控制方法.爆胎使得滚动阻抗系数和侧偏刚度等轮胎参数在短时间内产生剧烈的变化,从而导致转向控制失灵,进而引起无人驾驶车辆偏离道路甚至侧翻.为此,对无人驾驶车辆标称动力学模型进行反馈线性化,结合泰勒展开预测无人驾驶车辆的运动趋势.在此基础上,将爆胎引起的参数变化转化为不确定,利用模糊系统万能逼近原理,通过设计自适应模糊观测器进行在线观测.并同时考虑控制输入的饱和约束,利用连续预测控制方法设计解析控制律,以满足系统控制的实时性要求.最后,与传统非线性预测控制以及PID控制进行了仿真对比.从仿真结果可以看出,当车辆发生爆胎后,轮胎滚动阻抗系数瞬时增大了29倍、侧偏刚度瞬时降低了72%,如不施加额外的转向控制作用,无人驾驶车辆将在1s内偏离原车道约5.5m.而施加本文所提方法后,系统的实时性和控制性能均优于给定传统算法.一方面,与非线性预测控制和PID控制相比,所提方法计算速度提高了约150倍,计算时间缩短约50%;另一方面,在给定的控制输入饱和约束范围内,所提方法仍能够控制无人驾驶车辆在爆胎后只发生微小偏移,偏移量仅为传统算法的2.5%左右.
无人驾驶;爆胎;预测控制;模糊观测器
爆胎是指轮胎因破裂产生的干瘪以及胎压急剧减少至零等一系列现象,爆胎发生后车辆动力学特性突变,易引起车辆冲出道路边界或者侧翻等事故[1].根据美国公路交通安全管理局的数据[2],每年大约有78392起由于轮胎爆裂而导致的车祸,其中约414人死亡、10275人受伤.而高速公路是爆胎事故的频发地段,因为车辆长时间高速行驶时,轮胎的机械损伤和热损伤会快速累积导致轮胎的抗压性变差.因此高速公路上的爆胎控制研究有着重要的意义.
车辆爆胎产生最为显著的动力学特性变化为爆胎轮滚动阻抗系数的增加[3],从而使车辆偏向爆胎轮一侧行驶.除此之外,轮胎的有效半径和侧偏刚度等参数也会发生改变.在线胎压检测[4]是预防爆胎发生的有效手段,在爆胎发生前可以报警提示驾驶员,但这种被动预防手段不能从根本上解决问题,必须结合各类底盘控制系统才能改善车辆动态稳定性能.这类底盘系统包括防抱死制动系统[5]、主动前轮转向系统[6]等.但因这些系统都不是专门应对爆胎控制的,所以爆胎后控制效果一般,因此有必要进行爆胎控制算法研究.文献[7]提出了基于输入状态稳定的鲁棒控制方法解决爆胎控制问题,文献[1]对考虑约束的∞爆胎控制方法进行了研究,文献[8]提出了基于非线性预测控制(NMPC)的爆胎控制方法.前两种方法虽然实时性能和鲁棒性能突出,但是不能确保取得最优控制输入.预测控制(MPC)[9-10]是无人驾驶领域应用较为广泛的算法,虽然在线优化可以在满足多约束的情况下求出最优的控制输入,但是对计算硬件的负荷大、实时性的保障是一个有难度的问题.文献[11-12]提出的连续时域预测控制算法就很好地解决了这个问题,但不能考虑约束是该算法最大缺陷.
本文针对高速路段上的无人驾驶车辆的爆胎控制中实时性与控制性能难以同时满足的难题,将爆胎引起的参数变化转化为不确定项,并设计自适应模糊观测器在线观测,对车辆的动力学模型进行反馈线性化后,结合泰勒展开原理,设计了连续时域预测控制律.该控制律满足控制输入饱和约束以及实时性要求,仿真结果也证明了所提出控制系统的有效性.
1 动力学模型
前轮转向的无人驾驶车辆模型如图1所示,建立了两个坐标系,其中为地面惯性坐标系,为车体坐标系,为车辆的质心.

图1 无人驾驶车辆动力学模型
无人驾驶车辆的动态可描述为

(1)
式中:和I分别代表车辆的质量和转动惯量;和分别为质心侧偏角和横摆角;F、F和M分别为质心处的纵向合力、横侧向合力以及合外力矩.
F、F和M的表达式分别为
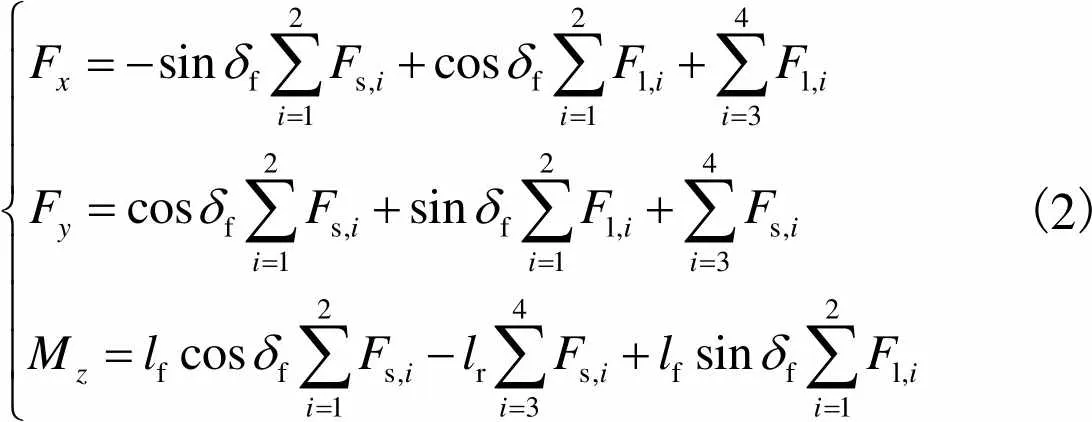
(2)
式中:f和r分别为前后轴与质心的距离;f为前轮偏转角;l和s分别为轮胎的纵向合力和横侧向合力;=1,2,3,4为轮胎编号,分别代表前左、前右、后左、后右轮胎.因为本文研究无人驾驶车辆在高速行驶时的机动问题,可以做如下假设.
假设1纵向滑移率以及质心处侧偏角和前轮偏转角都足够小,以至于可以对模型做简化得

(3)
式中:c,i、l,i和s分别为轮胎侧偏刚度、纵向刚度和滑移率;α为轮胎侧偏角.假设1成立时,α的计算公式为

(4)
式中为无人驾驶车辆的速度.最后整理式(1)~式(4)可以得到

(5)
2 爆胎后的车辆动态
轮胎爆胎后,胎压瞬时减少为0,引起滚动阻抗系数急剧增加以及侧偏刚度的降低,如图2所示.

图2 爆胎引起的参数变化
f0和c0为未发生爆胎时的滚动阻抗系数和侧偏刚度.爆胎轮滚动阻抗系数的变化引起左右轮的纵向力不相等,进而导致横摆角方向增加一个新的力矩驱使车辆偏向爆胎一侧行驶,同时侧偏刚度的变化也会引起爆胎轮侧向力的改变,爆胎后的无人驾驶车辆的动力学模型(假设1号轮爆胎)为
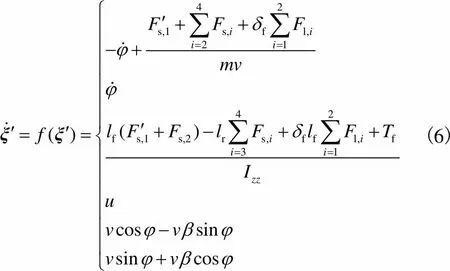
(6)

(7)

(8)
当后轮爆胎时,

(9)
式中:f和r分别为前后轴的宽度;f,i为滚动阻抗,且有

(10)
式中f,i和F分别为滚动阻抗系数和垂直载荷.
假设3爆胎后造成的车辆侧倾和俯仰对悬架结构的干扰足够小,不足以影响每个轮胎处的垂直载荷分布.
假设3成立时,前后轮的垂直载荷为

(11)
3 控制器设计
本文引入并改进了连续时域预测控制方法[12]并应用于无人驾驶车辆的爆胎控制.首先对爆胎前后的模型进行整合,然后根据自适应模糊观测器对因爆胎引入的不确定项进行观测,并基于最优目标距离准则设计连续时间预测控制器进行补偿,最终完成车道保持任务.
整合后的无人驾驶车辆动力学模型为

(12)
式中dis1和dis2为因爆胎引入的不确定项,且有

(13)
反馈线性化成立的必要条件是系统连续且足够光滑,显然系统(12)不满足条件,所以对标称模型(5)进行反馈线性化,然后通过对不确定项的观测实现输出的准确预测.
对模型(5)的输出逐次求解李导数,直至出现控制输入为止,即

(14)
其中

(15)
线性化后的系统可以整理为

(16)

(17)
得到线性化模型之后可通过泰勒展开原理预测p时间后的输出

(18)


(19)


(20)
进而设计目标函数在满足控制输入饱和约束的条件下,通过目标函数的最小化求得控制输入,其目标函数为


(21)


(22)
上述优化问题可以看作是二次规划问题,其中作为优化参数.考虑到爆胎是在车辆高速行驶时发生的紧急事件,一般的求解二次规划的方法很难满足在线计算的实时性要求,所以基于如下最优目标距离准则引理设计解析的反馈控制律.
引理1[13]针对一般的非线性系统

(23)

(25)
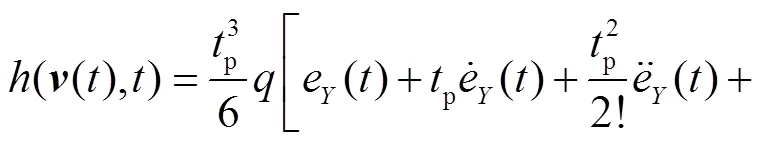
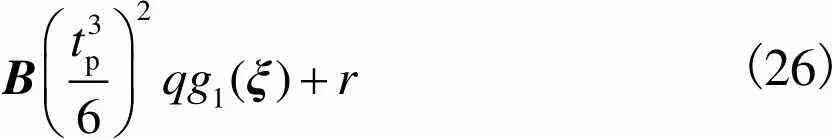
(26)

(27)

(28)
从式(26)可以看出本文中的T为对角阵,所以对应的解析控制律为


(29)


(30)

(31)
其中

(32)

(33)


(34)
成立.

(35)

(36)
将式(36)代入到式(35)中可以得到


(37)
设计自适应律为

(38)

(39)
4 爆胎控制仿真
本文研究的是前轮转向的无人驾驶车辆,车辆技术参数如表1所示.
表1 车辆技术参数

Tab.1 Vehicle technical parameters
先验证模型(12)与实际情况的趋近程度,图3为在惯性坐标系下,不进行转向控制时车辆质心纵坐标在2s内的变化.从图中可以看出,在1s的时间内,车辆向爆胎轮一侧产生了5.5m的侧偏,基本与实际情况一致.所以爆胎时的转向控制是必要的.

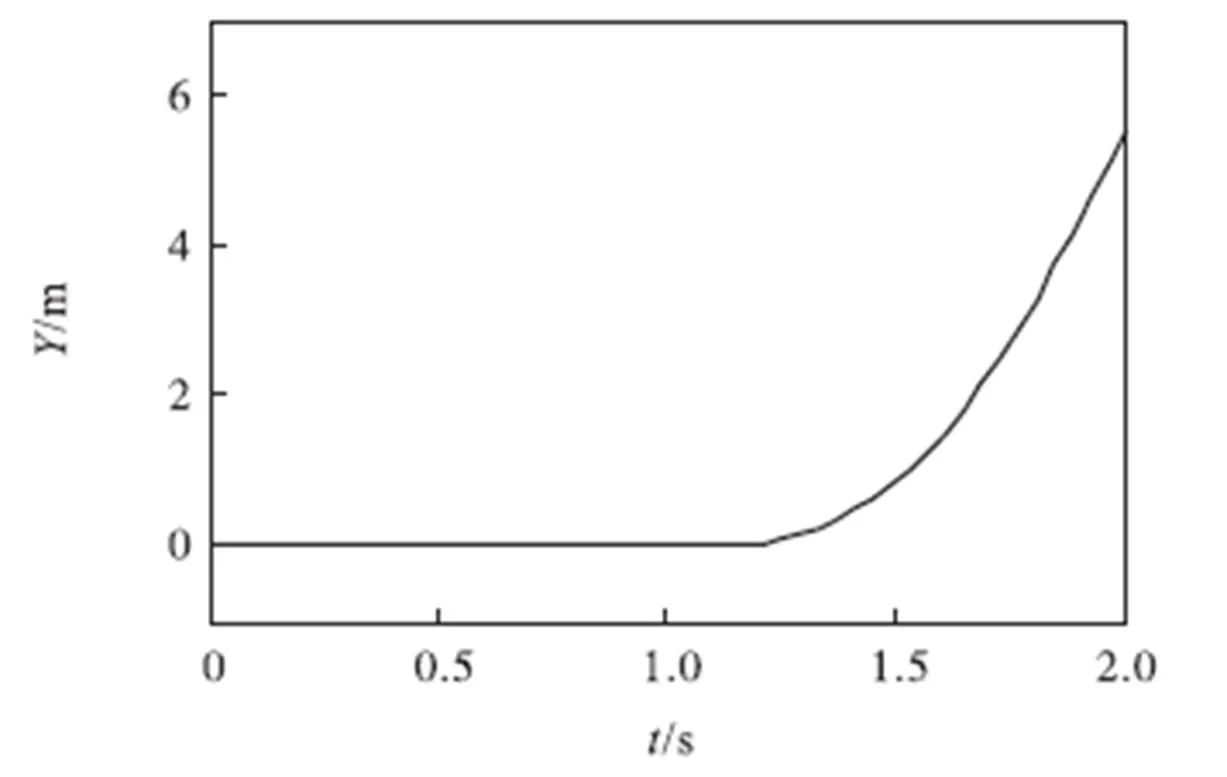
图3 惯性坐标系下车辆质心纵向位移

图4 本文方法下的车辆质心纵向位移
与图3对比,本文方法可以在爆胎发生时间未知的情况下控制车辆保持在当前车道上而不发生偏移,控制效果基本与文献[7]的结果有相同的满意度.总计算时间为5.64s,实时性也满足爆胎控制的需求.
图5为控制输入的变化情况,图中红色虚线为约束的上下界,从图中可以看出,控制输入严格满足控制输入饱和约束条件,并且车辆在发生爆胎后1.6s的时间内回复到了稳定的状态.
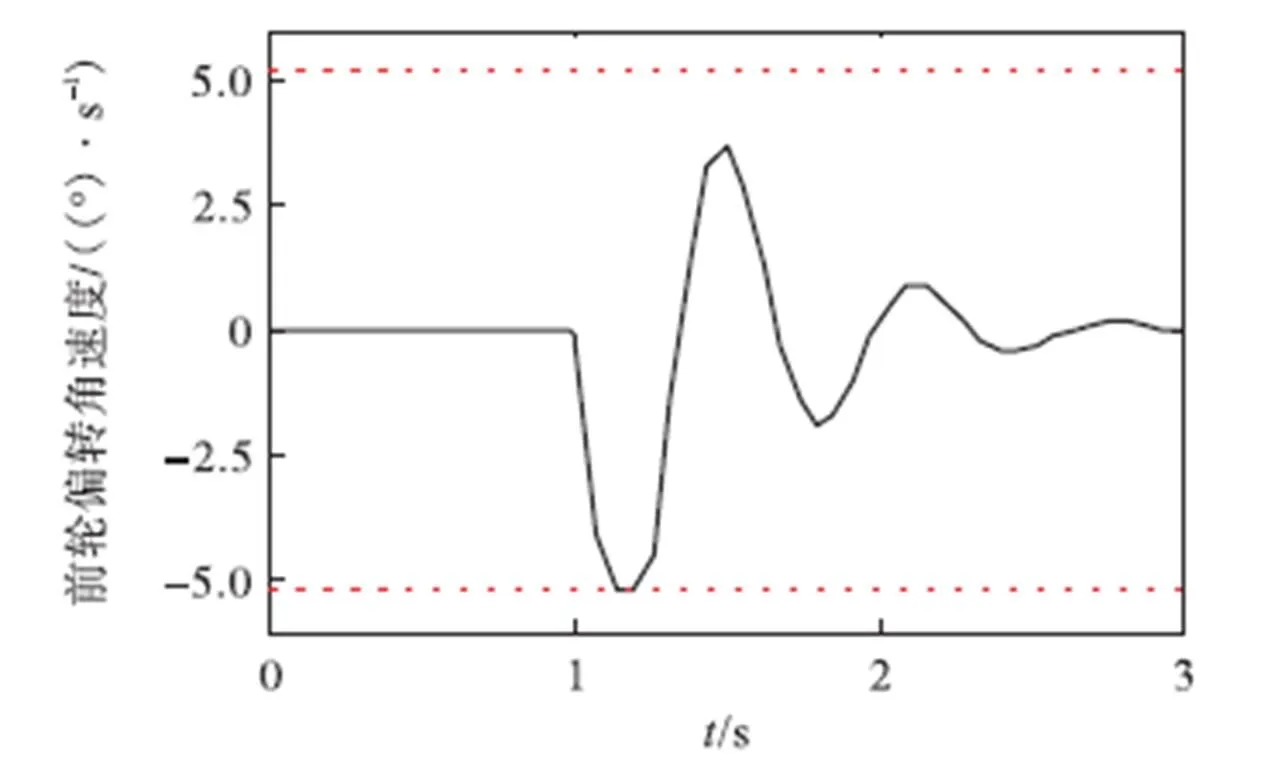
图5 前轮偏转角速度
图6为前轮偏转角的变化,从图中可以看出,前轮偏转角在爆胎发生1.6s后稳定在了0.8°.
为进一步说明本文提出方法的有效性,设计NMPC控制器以及PID控制器进行仿真对比,设置相同的输入约束,控制效果如图7所示.

图6 前轮偏转角

图7 NMPC和PID下的车辆质心纵向位移对比
虽然NMPC同样可以抑制车辆向爆胎轮一侧发生偏移并最终保持直行状态,但是存在8cm的稳态误差,而且相同情况下的在线优化总时间为859.76s,这在高速行驶情况下的爆胎控制中显然是不可取的.相比之下,PID的总计算时间为10.20s,虽然可以满足实时性的要求,但是控制效果不佳,不能完全抵消掉向爆胎轮一侧偏移的趋势.
总之,所提爆胎转向控制算法比NMPC计算速度提高约150倍,比PID控制算法计算时间缩短约50%,且可以控制无人驾驶车辆在爆胎后仅产生传统算法2.5%左右的偏移量.所提控制器不仅可以保证比一般控制方法更好的实时性,而且可以保证更好的控制效果,基本可以完全抵消爆胎的不良影响.
5 结 语
本文针对无人驾驶车辆爆胎后的转向控制问题,引入并改进了连续时域预测控制算法,使得解析的控制律满足控制输入约束.将爆胎引起的参数变化转化为不确定项,设计自适应模糊系统进行观测,同时对反馈线性化后的车辆动力学模型,利用泰勒展开预测输出形成二次规划问题,基于最优目标距离准则设计控制律.仿真结果证明了该方法可以在保证实时性的同时控制爆胎车辆保持当前的行驶方向.
[1] Wang F,Chen H,Guo H,et al. Constrained H∞control for road vehicles after a tire blow-out[J]. Mechatronics,2015,30:371-382.
[2] Choi E H. Tire-Related Factors in the Pre-crash Phase[R]. Washington,DC,USA:National Highway Traffic Safety Administration,2012.
[3] Tandy D F,Ault B N,Colborn J,et. al. Objective measurement of vehicle steering and handling performance when a tire loses its air[J]. SAE International Journal of Passenger Cars-Mechanical Systems,2013,6(2):741-769.
[4] Qian J,Kim D S,Lee D W. On-vehicle triboelectric nanogenerator enabled self-powered sensor for tire pressure monitoring[J]. Nano Energy,2018,49:126-136.
[5] Mirzaeinejad H. Robust predictive control of wheel slip in antilock braking systems based on radial basis function neural network[J]. Applied Soft Computing,2018,70:318-329
[6] Zheng B,Anwar S. Yaw stability control of a steer-by-wire equipped vehicle via active front wheel steering[J]. Mechatronics,2009,19(6):799-804.
[7] Wang F,Chen H,Cao D. Nonlinear coordinated motion control of road vehicles after a tire blowout[J]. IEEE Transactions on Control Systems Technology,2016,24(3):956-970.
[8] Wang F,Guo H,Chen H. Nonlinear model predictive control of blowout tire vehicles and its map-based implementation[C]// Chinese Control Conference. Hangzhou,China,2015:4043-4048.
[9] Ding B,Pan H. Output feedback robust MPC with one free control move for the linear polytopic uncertain system with bounded disturbance[J]. Automatica,2014,50(11):2929-2935.
[10] Zheng Y,Li S,Tan R. Distributed model predictive control for on-connected microgrid power management[J]. IEEE Transactions on Control Systems Technology,2017,26(3):1028-1039.
[11] Lu P. Optimal predictive control of continuous nonlinear systems[J]. International Journal of Control,1995,62(3):633-649.
[12] Panchal B,Kolhe J P,Talole S E. Robust predictive control of a class of nonlinear systems[J]. Journal of Guidance Control & Dynamics,2014,37(5):1437-1445.
[13] Barnard R. Continuous-time implementation of optimal-aim controls[J]. IEEE Transactions on Automatic Control,1976,21(3):432-434.
[14] Lee H,Tomizuka M. Robust adaptive control using a universal approximator for SISO nonlinear systems[J]. IEEE Transactions on Fuzzy Systems,2000,8(1):95-106.
Model Predictive Control-Based Steering Control of Unmanned Ground Vehicle with Tire Blowout
Hu Chaofang1, 2, 3,Cao Lei1, 2, 3,Zhao Lingxue1, 2, 3,Wang Na3, 4
(1. School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China;2. Key Laboratory of System Control and Information Processing of Ministry of Education,Shanghai 200240,China;3. Key Laboratory of Micro Opto-Electro Mechanical System Technology of Ministry of Education,Tianjin University,Tianjin 300072,China;4. School of Electrical Engineering and Automation,Tianjin Polytechnic University,Tianjin 300387,China)
To control the steering of unmanned ground vehicles with tire blowout,we designed a continuous-time adaptive model predictive control method that meets the requirements of real-time and control performance. In a very short period of time,tire blowouts cause drastic changes in the tire parameters,including the rolling resistance coefficient and cornering stiffness,which lead to steering control failure and deviation of the unmanned ground vehicle from the lane of travel or even a rollover. In this paper,we linearize a nominal dynamic model of an unmanned ground vehicle using feedback linearization,and predict the motion trend of the vehicle by Taylor expansion. On this basis,the parameter changes caused by the tire blowout are transformed into uncertainties,so we designed an adaptive fuzzy observer to perform on-line observation based on the universal approximation theorem of fuzzy systems. Using control input saturation constraints,we designed an analytic control law using continuous model predictive control to satisfy the real-time requirement of the control system. Finally,we performed simulations to compare the performance of the proposed method with those of traditional nonlinear model predictive control and PID control. The simulation results showed that,after a tire blowout,the tire rolling resistance coefficient experiences an instantaneous 29-fold increase,and the cornering stiffness experiences an instantaneous decrease of 72%. Without additional steering control,the unmanned ground vehicle would deviate from the original lane by about 5.5meters in one second. We validated that the system using the proposed method exhibited better real-time and control performance than those using the traditional algorithms. We found the proposed method to improve the computing speed 150-fold and to cut the computing time 50%,respectively,compared to the nonlinear model predictive control and PID algorithms. In addition,the proposed method can guarantee that the vehicle experiences only a slight deviation from its lane of travel after a tire blowout within the given control input saturation constraints,with the deviation being only about 2.5% of that of the traditional algorithm.
self-driving;tire blowout;model predictive control(MPC);fuzzy observer
10.11784/tdxbz201809084
TP2
A
0493-2137(2019)05-0468-07
2018-09-26;
2018-11-06.
胡超芳(1973— ),男,博士,副教授.
胡超芳,cfhu@tju.edu.cn.
国家自然科学基金资助项目(61773279);系统控制与信息处理教育部重点实验室开放课题基金资助项目(Scip201608);微光机电系统技术教育部重点实验室(天津大学)开放基金资助项目(MOMST 2016-4).
the National Natural Science Foundation of China(No. 61773279),the Research Foundation of Key Laboratory of System Control and Information Processing of Ministry of Education(No. Scip201608),the Open Project of Key Laboratory of Micro Opto-Electro Mechanical System Technology of Ministry of Education(Tianjin University)(No. MOMST 2016-4).
(责任编辑:孙立华)

