再谈区间端点赋值的合理性
甘肃省兰州市第五中学 (邮编:730000) 甘肃省兰州新区舟曲中学 (邮编:730087)
函数的零点是函数的重要概念,特别地,由于在导函数的变号零点两侧导函数值的正负不相同,函数的单调性不相同,所以导函数的零点在解决函数的单调性中起着决定性的作用. 但是有些问题,首先需要判断导函数的变号零点是否存在,这就需要借助零点存在性定理构造一个区间,使得区间端点导函数值异号,那么,有些试题答案中的区间端点为何偏偏就是那两个数据呢?取点很巧妙,方法来得很突然[1],是偶然还是另有玄机,文1给出了区间端点赋值的常见方法,本文通过几道函数与导数综合题的探析,再次给出几种取点赋值的方法.
1 根据已知条件给定的区间,直接得到赋值的区间端点
例1(2018年四川省遂宁市高三第二次模拟考理科)已知函数f(x)=(x-2)ex-a.
(1)若函数f(x)在[0,2]有两个零点,求实数a的取值范围;
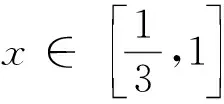
解(1)f′(x)=(x-1)ex.
当0 当1 令g(x)=(x-2)ex-x+lnx+1,下面求函数g(x)的最小值, 当x0 例2(2013年全国卷2第21题)已知函数f(x)=ex-ln(x+m). (1)设x=0是f(x)的极值点,求m的值,并讨论f(x)的单调性; (2)当m≤2时,证明f(x)>0. 当-1 (2)令g(x)=ex-ln(x+2)(x>-2), 由于f(x)=ex-ln(x+m)≥ex-ln(x+2)(m≤2),故只需证明g(x)>0即可. 当-2 当x>x0时,g′(x)>0,g(x)单调递增. 评析本题判断g′(x)零点的时候,选择的区间端点为什么右端点赋值为x=0呢?由切线不等式ex≥x+1, 故x≥0,或x≤-3(舍), 例3(四川德阳市2018届高三第二次诊断数学(理)试题)已知函数f(x)=a+lnx2,且f(x)≤a|x|. (1)求实数a的值; 解(1)令g(x)=f(x)-a|x|,则g(x)=g(-x). 当0 故g(x)≤g(1)=0,符合题意,因此a=2. 令h(x)=x-2lnx-4, 故h(x)单调递增,h(8)h(9)<0,∃x0∈(8,9)使得h(x0)=x0-2lnx0-4=0. 当2 当x>x0时,h(x)>0,g′(x)>0,g(x)单调递增. 则f(m)=m-2∈(6,7). 评析h(8)h(9)<0是怎么来的呢?事实上,根据已知条件结合推理过程,在(2,+∞)内,函数g(x)先减后增,所以g(x)min的最小值只能是在极小值点x0处取得,并且g(x)min=g(x0)=x0=m,因此要证明f(m)=m-2=x0-2∈(6,7),只需证明x0∈(8,9)时,h(8)h(9)<0,从结论上推导得出了零点存在的区间端点赋值的合理性. 例4(2018北京市西城区高考一模数学(文)试题)已知函数f(x)=ex(a+lnx),其中a∈R. (2)记f(x)的导函数为g(x), 当a∈(0,ln2)时,证明:g(x)存在极小值点x0,且f(x0)<0. (1)函数区间端点的赋值问题,本质考查导函数的零点存在性定理,纵观这几年高考试题和一些省市的高三诊断试题,落脚点几乎都在判断导函数零点是否存在的特殊情况,即单调函数存在零点时,最多只有一个零点.并且当条件中的区间为开区间时,函数的最值一定在导函数的零点x0处取得;同时,在得到导函数存在零点之后,常借助导函数在x0处的值为0,实现超越式和其他代数式的转化,是化归思想指导解题的有力体现. (2)含参数的函数的区间端点赋值问题,参数是困惑函数取点的主要矛盾,可根据已知条件中参数的范围,合理放缩,去掉参数,转化为不含参数的函数的区间端点赋值问题.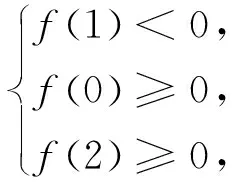
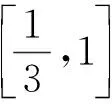
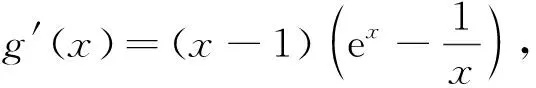
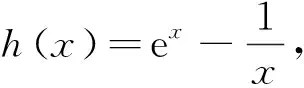
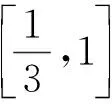
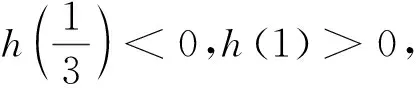
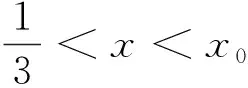
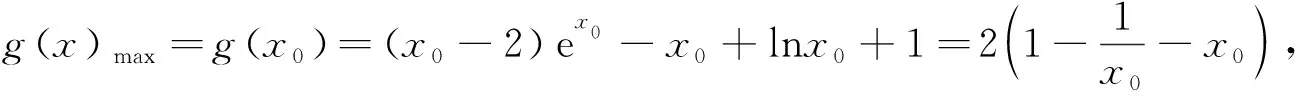
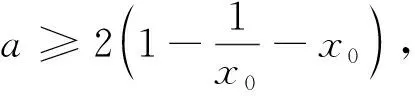
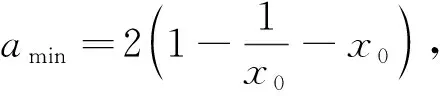
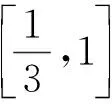
2 利用切线不等式变化得到的常见不等式,寻求赋值的区间端点
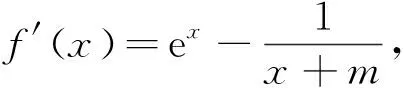
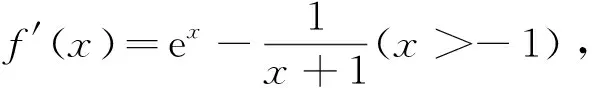
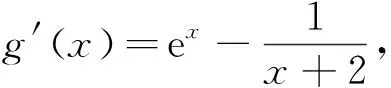
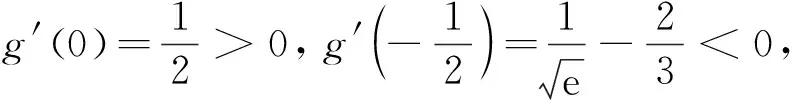
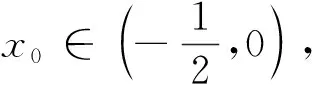
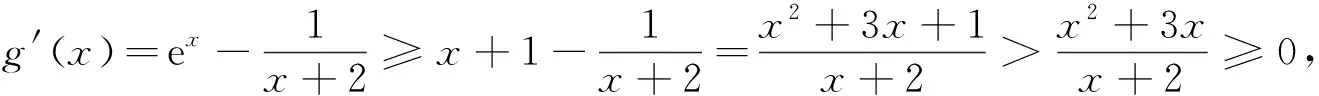
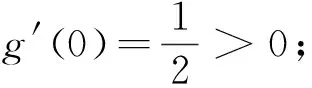
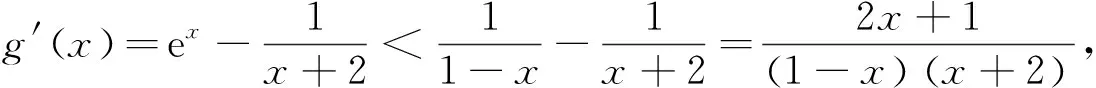
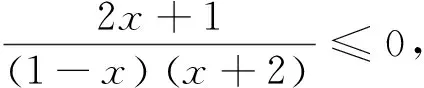
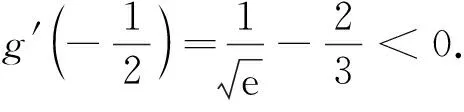
3 执果索因,推导出合理赋值的区间端点
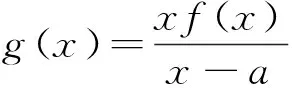
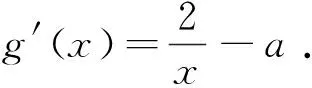
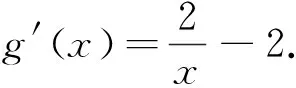
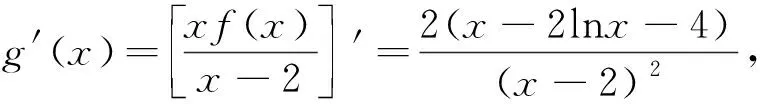
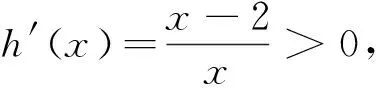
4 参数放缩与切线不等式齐发力,得到赋值的区间端点
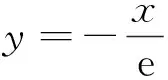
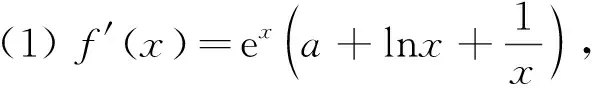
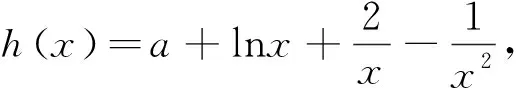
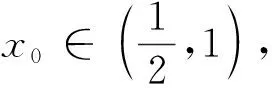
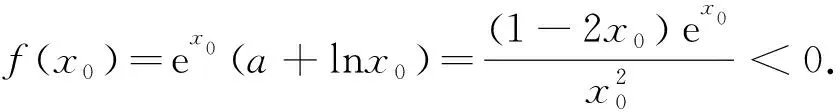
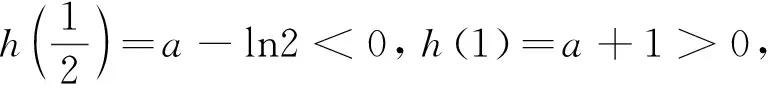
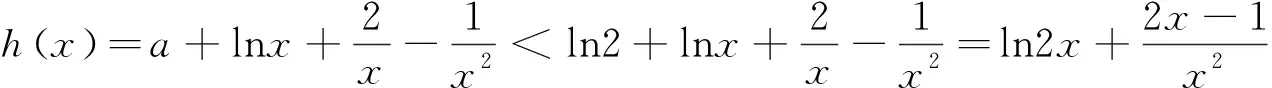
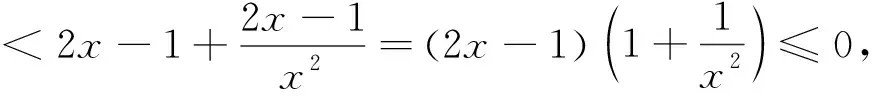
5 几点感悟