再谈编拟习题时应注意问题的存在性

北京丰台二中 (邮编：100071)

拙文[1]通过9道例题阐述了“编拟习题时应注意问题的存在性”的观点，本文再通过7道例题进一步阐述这一观点.

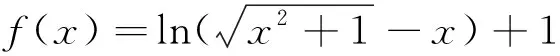
笔者的分析编题者没有给出这道题的答案.

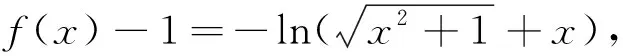
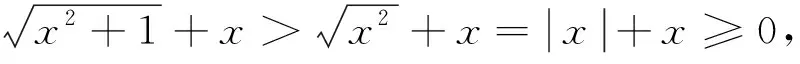
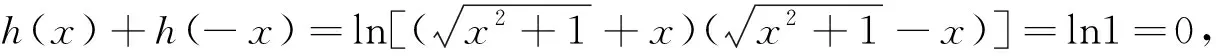
所以h(x)是奇函数.因为

所以h(x)是减函数.

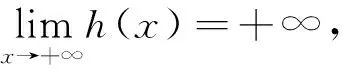
对此题的分析，再一次说明了编拟习题时应注意问题的存在性.

例2(《高中数学同步检测三级跳(必修5)》(李振雷主编，中国财政经济出版社，2010年出版，2015年印刷)第36页第10题)设数列{an}(n=1，2，3，…)的前n项和Sn满足Sn=2an-a3，且a1，a2+1，a3成等差数列，求数列{an}的通项公式.

常规解法由题设Sn=2an-a3(n∈N*)，可得an=Sn-Sn-1=2an-2an-1(n≥2)，

an=2an-1(n≥2)，

从而a2=2a1，a3=2a2=4a1.

又因为a1、a2+1，a3成等差数列，即a1+a3=2(a2+1).

所以a1+4a1=2(2a1+1)，解得a1=2.

所以数列{an}是首项为2，公比为2的等比数列，得an=2n.

注下面再给出该题的另一种解法：

由题设Sn=2an-a3(n∈N*)，可得

a1=S1=2a1-a3,a1=a3，

a1+a2=S2=2a2-a3=2a2-a1,a2=2a1，a1+a2+a3=S3=2a3-a3=a3,a2=-a1，

所以a2=2a1=-a1,a1=0.

在常规解法中已得到an=2an-1(n≥2)，所以an=a1·2n-1=0(n∈N*).

但an=0(n∈{N*)不满足后面的题设“a1，a2+1，a3成等差数列”，说明题设有多余[2]，建议去掉后面的题设.

题4(很可能有印刷错误)可能源于2015年高考四川卷文科、理科第16(1)题：

设数列{an}(n=1，2，3，…)的前n项和Sn满足Sn=2an-a1，且a1，a2+1，a3成等差数列.

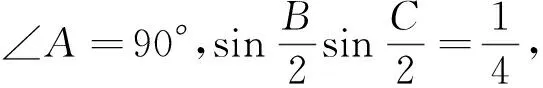
常规解法设AB=c,BC=a,CA=b.在△ABC中，角B、C的平分线分别是BD、CE.

笔者的分析本题是道错题.因为可证得：

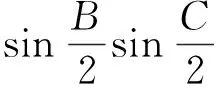
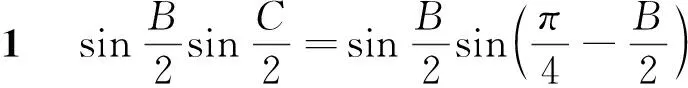
进而可得欲证结论成立.

可得欲证结论成立.

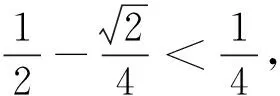
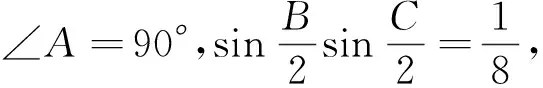
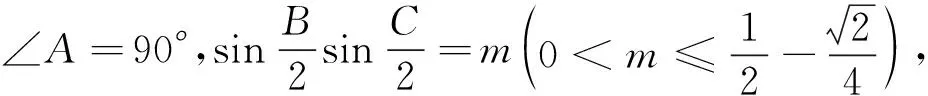
例4(2013年高考浙江卷理科第15题)设F为抛物线C:y2=4x的焦点，过点P(-1,0)的直线l交抛物线C于两点A、B，点Q为线段AB的中点，若|FQ|=2，则直线的斜率等于______.

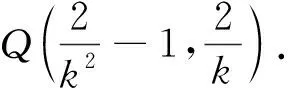
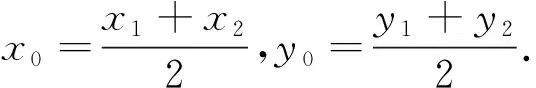
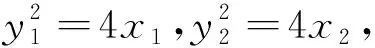
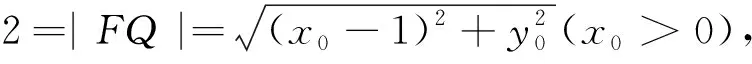
笔者的分析求得kAB=±1后，还应检验它是否满足题设“过点P(-1,0)的直线l交抛物线C于两点A、B”.事实上，此时直线l与抛物线C相切(即两点A、B重合)，说明所求直线的斜率不存在.

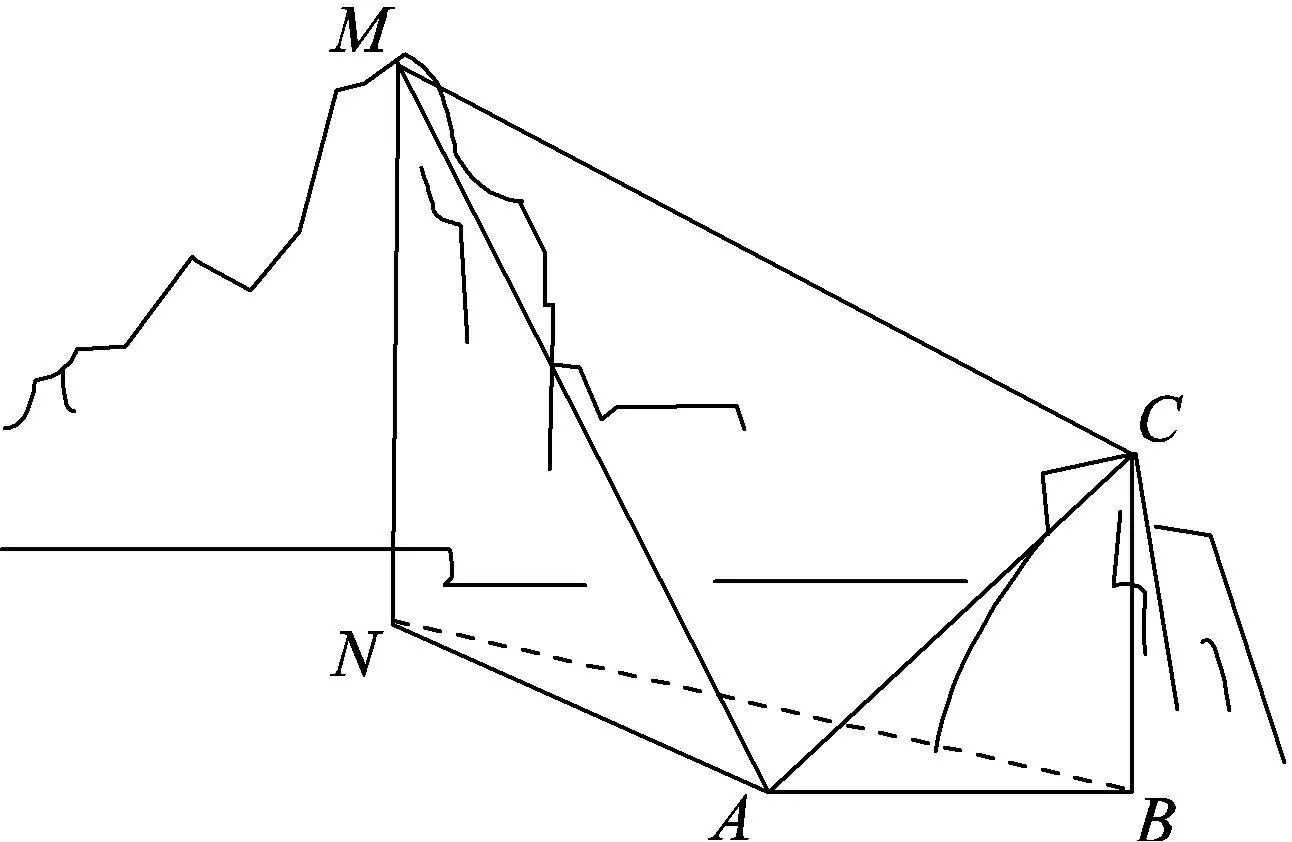
图1

例5(2014年高考全国新课标卷Ⅰ文科第16题)如图1，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=45°，以及∠MAC=75°，从C点测得∠MCA=60°.已知山高BC=100 m，则山高MN=______m.

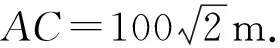
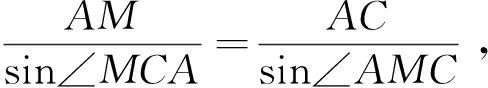
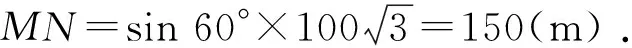
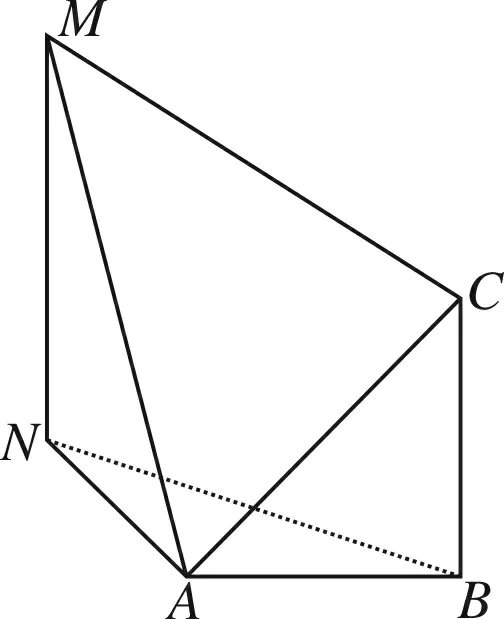
图2

笔者的分析 我们先证明

定理2 (1)若三条射线SA、SB、SC不共面，则∠ASB+∠BSC>∠ASC；

(2)底面是凸多边形的棱锥在顶点处的所有顶角之和小于周角.

证明当∠ASB≥∠ASC时，可得欲证结论成立.

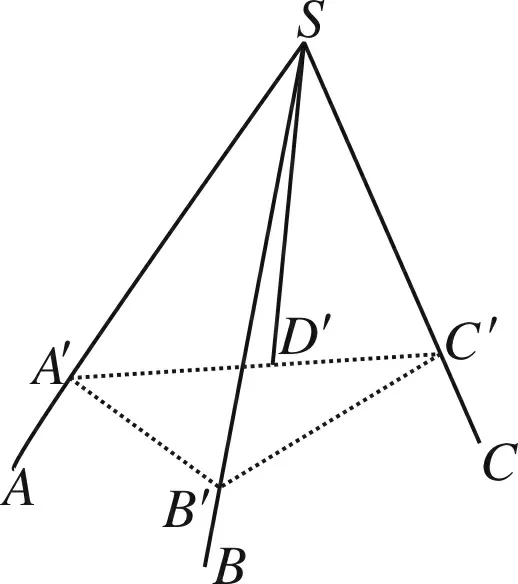
图3

当∠ASB<∠ASC时，如图3所示，可在∠ASC内(包括端点S)作∠ASB=∠ASD′，再在射线SB,SD′上分别截取相等的线段SB′,SD′.又过点B′,D′作平面分别与射线SA、SC交于点A′、C′.

进而可得△SA′B′≌ △SA′D′(边角边)，所以A′B′=A′D′,∠ASB=∠ASD′.

在△A′B′C′中，可得A′B′+B′C′>A′C′=A′D′+D′C′,B′C′>D′C′.

在△SB′C′与△SD′C′中，由余弦定理可得cos∠B′SC′∠D′SC′,∠BSC>∠D′SC.

所以∠ASB+∠BSC>∠ASD′+∠D′SC=∠ASC.

(2)下面只证明五棱锥S-ABCDE的情形.如图4所示，由定理2(1)可得

∠SAE+∠SAB>∠EAB；

∠SBA+∠SBC>∠ABC；

∠SCB+∠SCD>∠BCD；

∠SDC+∠SDE>∠CDE；

∠SED+∠SEA>∠DEA.

把它们相加后，由三角形、五边形内角和定理可得

5π-(∠ASB+∠BSC+∠CSD+∠DSE+∠ESA)>3π，

∠ASB+∠BSC+∠CSD+∠DSE+∠ESA<2π，

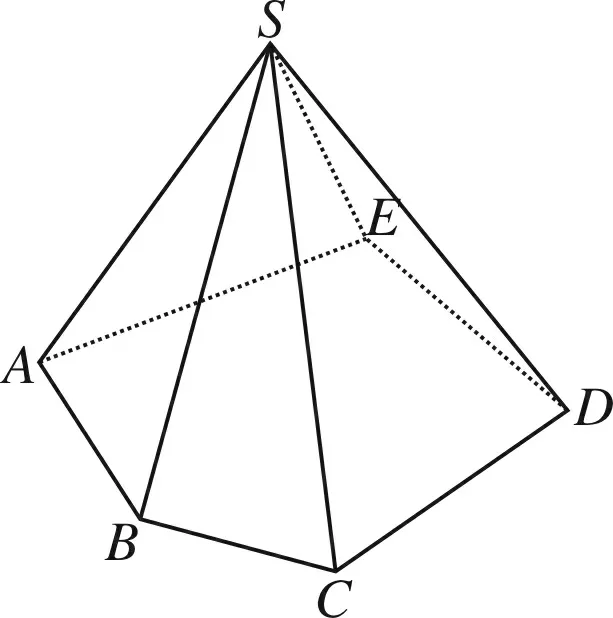
图4

得欲证结论成立.

下面再来分析上面的这道高考题及其解法.

如图5所示，延长MN至M′，使得NM=NM′，延长CB至C′，使得BC=BC′.

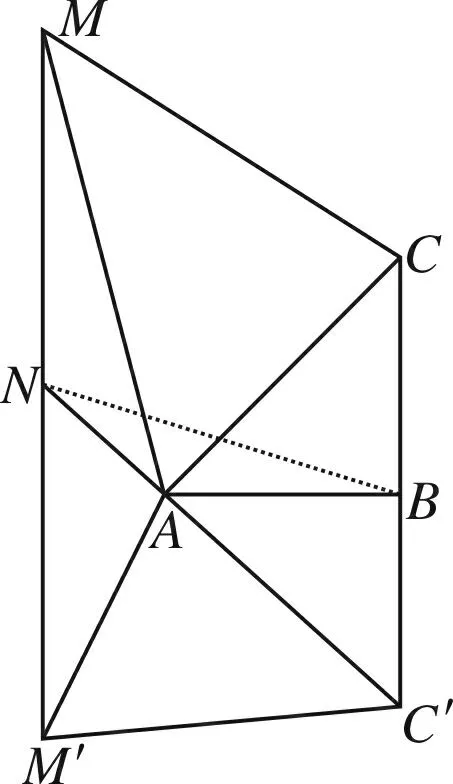
图5

进而可得Rt△ANM≌Rt△ANM′，∠NAM=∠NAM′,AM=AM′；还可得Rt△ABC≌Rt△ABC′，∠CAB=∠C′AB,AC=AC′.

可得四边形CBNM≌四边形C′BNM′，所以CM=C′M′，进而可得△ACM≌△AC′M′(边边边)，∠MAC=∠M′AC′.

所以∠NAM′+∠M′AC′+∠C′AB=∠NAM+∠MAC+∠CAB=60°+75°+45°=180°，

∠MAM′+∠M′AC′+∠C′AC+∠CAM=180°·2=360°.

进而可得凸四棱锥A-MCC′M′在顶点A处的所有顶角之和为周角，这与定理2(2)相矛盾！

这就说明这道高考题中的图1不准确，即在图1中不存在四棱锥A-BCMN，即点A应当在线段BN上.

下面再用另一种方法说明点A应当在线段BN上.

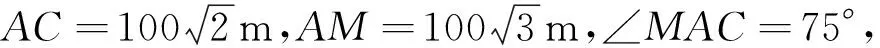
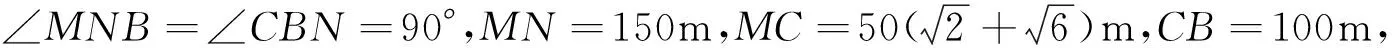
例5出错的原因是没有注意到满足题设的四棱锥A-BCMN不存在.

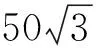
例6(1987年高考全国卷理科第15题)一个正三棱台的下底和上底的周长分别为30cm和12cm，而侧面积等于两底面积之差，求斜高.

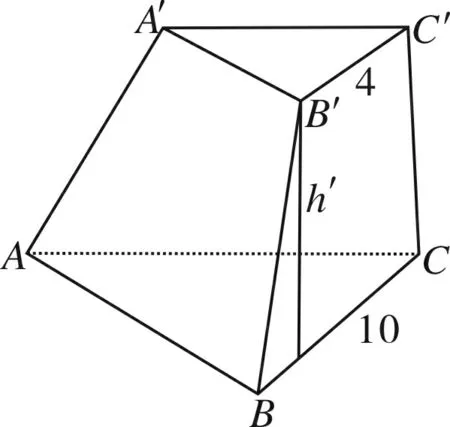
图6

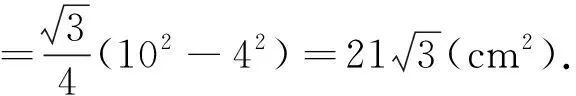
(其中h′是正三棱台的斜高)，

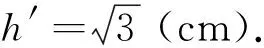
笔者的分析以上解法貌似严谨无误，但该题却是一道错题——错在满足题设的正三棱台不存在！

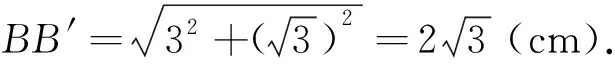
图7

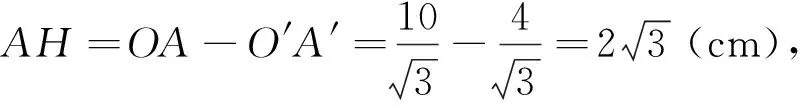
如图8所示，分别作点A′、B′、C′在平面ABC上的射影A″、B″、C″，可得点A″、B″、C″均在△ABC内，再由射影面积公式可得

S等腰梯形ABB′A′>S四边形ABB″A″,S等腰梯形BCC′B′>S四边形BCC″B″,S等腰梯形CAA′C′>S四边形CAA″C″，

(易证三个四边形ABB″A″,BCC″B″,CAA″C″均是等腰梯形且两两全等).

把它们相加后，即得正三棱台的侧面积大于下底面积与上底面积之差.

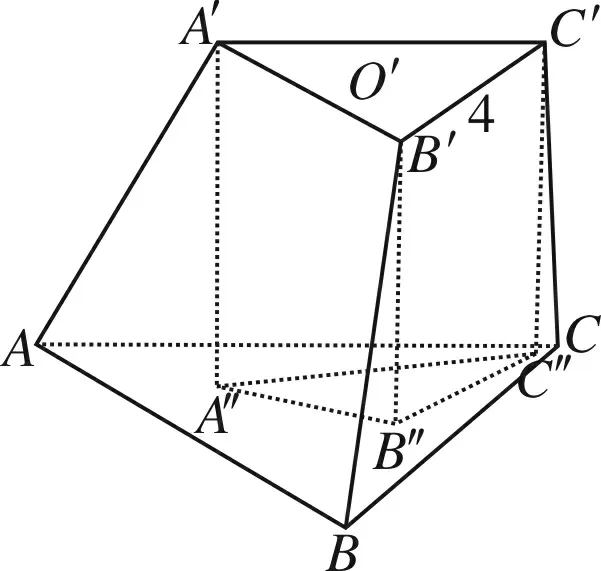
图8

同理，还可证得：

(1)正棱台的侧面积大于下底面积与上底面积之差；

(2)若一个棱台的上底面在下底面上的射影在下底面内，则该棱台的侧面积大于下底面积与上底面积之差.

(3)三棱台的侧面积大于下底面积与上底面积之差(可分上底面恰有0个、1个、3个顶点在下底面上三种情形获证).

猜测棱台的侧面积大于下底面积与上底面积之差.