微探究 深理解 提素养

江苏省徐州市第一中学 (邮编：221140)

学生在数学的学习过程中常常会出现“听起来头头是道，做起来莫名其妙”的现象．在教师的教导下，学生做了大量的题，见识了不同寻常的新奇解法，但碰到新题的时候又会一筹莫展．这与我们的大容量、快教学有着很大的关系．学生在教师的“过度”指导下，更多地是模仿，而少有思考．我们的课堂教学应该“慢”下来，在核心内容与重点问题上，给学生足够的思考时间与空间，放手让学生“大展拳脚”，触发学生的思维，激发学生的学习潜能.

微探究是围绕某个小知识点或某一问题，以学生已有的知识和经验为基础的数学探究活动．教师根据教学内容，精心设定问题，在课堂上组织学生进行“微”探究，对问题进行刨根问底，对解法进行对照优化，促使学生将知识转化为能力，将经验提升为素养.

在一次直线与圆的复习课上，学案中有如下一道题(2014年高考新课标Ⅱ卷理科第16题)，虽然是填空题中的压轴题，但结果却很容易得到．经了解，学生对本题有着繁简各异的处理方式，或“投机取巧”，或“纵横联想”，思考的出发点不尽相同．因此有必要创设探究环境，让学生在多角度分析与本质探寻的过程中，合作交流，碰撞思维，互相提升.

1 问题呈现

题目设点M(x0,1)，若在圆O：x2+y2=1上存在点N，使得∠OMN=45°，则x0的取值范围是______.

本题中的点M、N分别是直线、圆上的动点，可以看成是双变量问题，有一定的思维难度．不过因为∠OMN的特殊性，学生可以轻易(浮于表面)获得答案.

2 问题探究

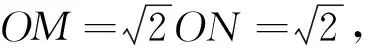
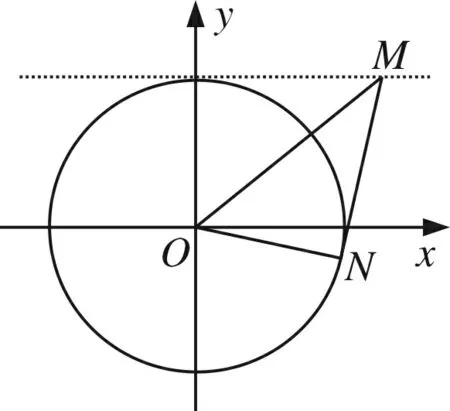
图1

师：为什么∠OMN变大了？

生1：当点M向y轴移动时，OM越来越短，所以∠OMN的正弦越来越大，因此∠OMN越来越大.

师：也就是说，当N为切点时的∠OMN不小于45°时，圆O上就一定存在满足题意的点N.我们如何来刻画∠OMN≥45°呢？

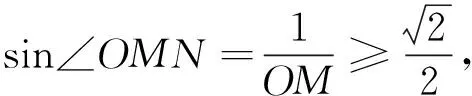
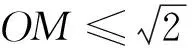
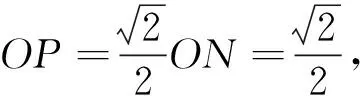
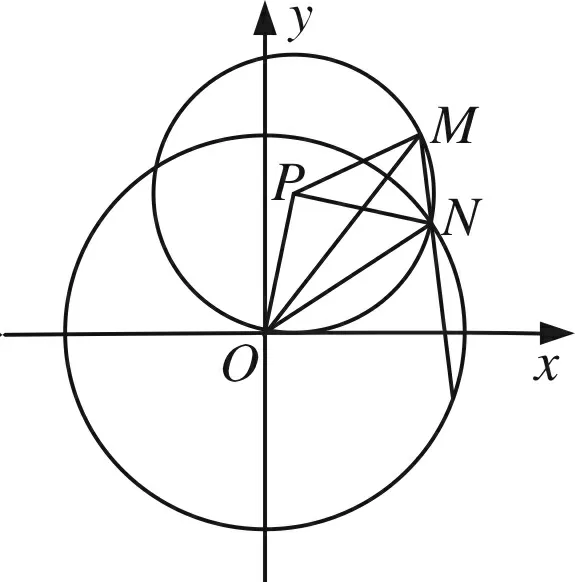
图2

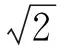
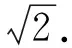
师：很好！说理要严谨，尤其是结合图形的叙述，你是怎样想到圆P的呢？

生3：因为△OMN的边ON与其所对的角都是定的，所以可把这个三角形放在一个圆内，∠OMN就是同弦所对的圆周角了.

师：哦，随着点M的移动，△OMN随之变化，而生3抓住了这一变化中的不变量，将OM作为一个等腰三角形的底边．而腰长又是确定的，所以OM的最大值随之即来.

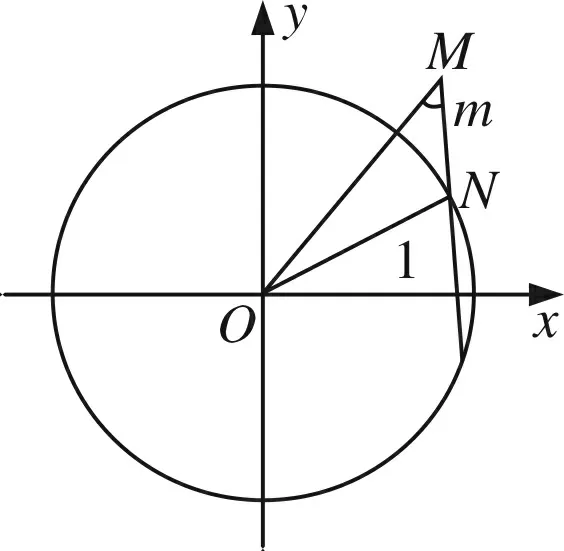
图3

师：很好．将点N的存在转化为MN长的有解．通过三角形的边角关系得到m与x0的等量关系，继而将问题转化为含参的一元二次方程有解问题．不过，该方程只要有解就行了吗？

师：嗯，注意转化的等价性哦．两根中的哪一个是m的值呢？

生4：有一个就行吧．(略作思考)因为直线MN与圆O相交，两个点都可以是N，所以两个根都是m的值.

师：△=0的时候呢？

生4：直线MN与圆O相切，N是切点，m只有一个值.

师：非常好！理，越理越清晰．形的角度“点的存在”与数的角度“方程有解”形成了完美对应，妙哉！

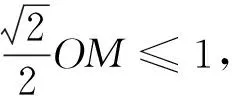
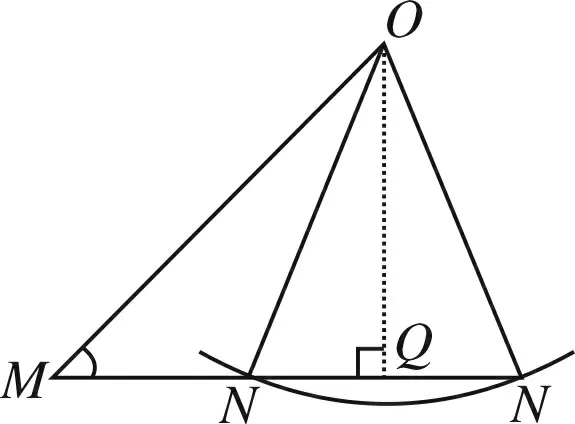
图5

师：噢，原来本题是由一道三角形有几解的问题改编而来．从圆的角度看，其实，点N是直线MN与圆O的公共点，因此“存在点N”可看成是直线MN与圆O相交或相切，所以圆心O到直线MN的距离小于或等于半径，也就是OQ≤ON.殊途同归啊！

3 探究感悟

在普通高中数学课程标准(2017年版)中，“数学建模活动与数学探究活动”作为必修课程与选择性必修课程的主题之一，旨在通过发现与提出问题、分析与解决问题的综合实践活动促进学生思维能力、实践能力和创新意识的发展，提升数学学科核心素养．探究应成为教师组织教学活动的基本意识，精心设计课堂“微”探究活动，让学生经历艰苦探究、惊喜发现、享受数学的探究过程，使探究成为学生的一种习惯，指导学生后续的自主成长．为高质量地实施微探究，教师应做问题的开发者、活动的参与者、学生的引路人.

3.1 做问题的开发者

美国数学家哈尔莫斯曾说：“数学真正的组成部分应该是问题和解，解题才是数学的心脏．”数学探究活动是围绕某个具体的数学问题，开展自主探究、合作研究并最终解决问题的过程．问题是实施数学探究的载体，也是关键，选好问题是进行数学探究的第一步．教师应精选问题，研究透彻，以便在课堂微探究活动中充分发挥问题的价值．一个好的问题应该富有启发性、趣味性、挑战性、开放性、探索性等特点，能吸引学生的目光，使学生“纵横联想”所学知识与方法进行多角度分析与求解．本题的解法多样，看似考查直线与圆的位置关系，实又涉及解三角形、函数与方程、几何最值等多方面的知识．生5的解法正是基于课本(必修5)中对三角形有几解的探究经验，因此也探寻到了本题的课本之源.

3.2 做活动的参与者

教师应居高临下地设计教学，俯下身来参与课堂活动．叶澜教授曾说：“课堂是向未知方向挺进的旅程，随时都有可能发现意外的通道和美丽的因素，而不是一切都必须遵循固定路线而没有激情的行程．”教学过程是复杂的、丰富多变的，教师应善待课堂上随时出现的“意外”．本节课中，题目的常规解决就是极端位置分析(生1的解法)或转化为直线与圆有公共点(教师最后总结出)，对于学生对∠OMN=45°的“别开生面”的刻画，教师没有制止，而是尊重学生的“第一思考权”，让他们一一说完，最后却惊现了问题的本质，殊途同归．在师生、生生、生本交流的过程中，学生的思维被激发，思想在碰撞，甚至有学生想到了利用“到角公式”来求直线MN的斜率．多给学生“想一想”的时间，多与学生进行平等地交流，将充分调动学生思维，于学生成长大有裨益.

3.3 做学生的引路人

著名教育家叶圣陶先生曾说：“我以为好的先生不是教书，不是教学生，乃是教学生学．”我们的课堂教学应追求数学思想的渗透、通性通法的提炼、思维习惯的培养，使学生在参与探究活动的过程中形成科学的探究方法，能够在后续的学习过程中自主开展数学探究活动．本节课中，题目的解决始于学生的“投机取巧”，教师不断地追问，促使学生想清楚、说明白，并就此引导学生进行一般性探究．学生经历了从特殊到一般，从复杂到简单，从模糊到清晰的系列过程，可以说还原了探究的真实过程．在追问中，学生的念头逐渐清晰；在联系中，知识的体系逐渐完善；在求简中，学生的思维得以历练；在探寻中，问题的本质得以揭示；在活动中，学生的学习获得独立．我们应致力于将学生引到科学探究之路，自主发展之路，素养自育之路.