曲线轨道参数对钢轨振动衰减率的影响研究

刘卫丰， 杜林林， 刘维宁

(北京交通大学 土木建筑工程学院， 北京 100044)

铁路交通和城市轨道交通在方便居民出行的同时，也存在一些环境影响问题，最主要的问题之一就是列车运行引起的振动与噪声影响。其中，轮轨噪声和车内噪声是最主要的噪声影响之一。尤其是在曲线轨道地段，列车运行引起的振动与噪声往往要比直线地段要大。而且，曲线轨道的轮轨相互作用比直线轨道复杂得多，也会产生多种轨道振动与噪声问题，例如钢轨波磨、曲线啸叫等[1-3]。

钢轨振动衰减率是一个重要的钢轨动态参数，定义为：钢轨振动沿钢轨纵向能量(振幅)传递的变化率，以dB/m为单位，它反映了在某种轨道结构中，钢轨振动沿纵向的综合衰减能力，分为竖向振动衰减率和横向振动衰减率[4]。它已成为评判轨道声学特性的一个重要指标，是钢轨的有效声辐射长度的重要控制指标。当钢轨振动幅值一定时，衰减率越大，振动沿钢轨纵向衰减越快，钢轨的声功率也越低。另外，它可以用来表示轨道结构的阻尼特定，即在某些频段内抑制钢轨振动的能力。钢轨振动衰减率越大，说明轨道系统的阻尼越大。如果钢轨振动衰减率过低(小于0.1 dB/m)，表示钢轨有脱离扣件约束进行自由振动的趋势。钢轨振动过大可能引发和加剧波磨损害，严重时可能会使扣件松脱及弹条断裂，例如，北京地铁4号线、5号线、10号线等线路上剪切型轨道减振器上出现的钢轨波磨问题就符合这样的特征[5-7]。国外学者对钢轨振动衰减率进行了一系列研究，主要研究了钢轨振动衰减率的工程意义、测试方法、影响因素等[8-9]。另外，钢轨振动衰减率也作为衡量钢轨阻尼器减振和降噪效果的重要指标[10-12]。

对于曲线轨道的研究，近年来国内外学者已经开展了一些工作。Kostovasilis等[13]利用一个曲线轨道有限元模型比较了曲梁单元和直梁单元在计算曲线轨道动力响应上的差异。在另外一篇论文中，Kostovasilis等[14]建立了一个考虑竖向/横向相互作用的曲线轨道动力解析模型，并讨论了曲线轨道的竖向/横向耦合效应问题。Ang等[15]采用三角函数逼近法推导了移动荷载作用下黏弹性地基上的曲线轨道动力响应的解析解。李克飞等[16-18]基于Duhamel积分和动力互等定理推导了移动荷载作用下曲线Timoshenko梁平面外振动响应的解析解。Zhang等[19]在李克飞的研究基础上，通过引入了车辆模型计算了移动列车引起的轨道的动力响应。

通常，铁路轨道的钢轨被轨枕或扣件周期性离散支承，所以许多学者都把周期性的概念引入到轨道的动力模型中。例如Gry等[20]基于梁的广义横截面位移法提出一个周期性铁路轨道模型并分析了此模型的适用性。Sheng等[21-22]把钢轨考虑为无限长周期性Euler梁，推导了在固定荷载作用下钢轨动力响应的解析解。Clouteau等[23-25]基于Floquet变换建立了一个周期性轨道-隧道-地层的有限元-边界元耦合模型，并计算了固定荷载和移动荷载作用下多种轨道、隧道结构以及地层的动力响应。马龙祥[26]利用无限周期性结构理论推导了地铁轨道中的普通整体道床轨道和浮置板轨道动力响应的解析解。

上述文献中的周期性理论均是应用到直线轨道，本文提出一个周期性曲线轨道解析模型，该模型中，钢轨考虑为曲线Timoshenko梁，支承于周期性离散分布的扣件上。利用此模型，可计算固定谐振荷载作用下钢轨的振动速度频响函数，然后据此计算出钢轨的振动衰减率。并讨论了扣件刚度、扣件阻尼、扣件间距和曲线半径对曲线钢轨振动衰减率的影响。

1 周期性曲线轨道动力响应推导

本文的曲线Timoshenko梁具有如下假定：① 曲线梁为等截面的匀质梁；② 曲率半径为常数，梁的横截面具有竖直的对称轴；③ 忽略曲线梁的翘曲变形。曲线梁的坐标系符合右手螺旋法则规定，如图1所示，图中，R为曲线半径，ux、uy和uz分别为x,y,z三个方向的位移，φx,φy和φz为绕三个坐标轴的转角。在曲线钢轨的轨头上作用两个移动的单位谐振荷载eiwFt，速度为v，如图2所示，图中C点为钢轨的形心，S点为钢轨的剪切中心，扣件的竖向支承和横向支承作用于轨底上，而扭转支承作用于剪切中心S点上。由于作用在轨头B点上的荷载可以等效为一个作用于钢轨形心C点的横向荷载(属于平面内荷载)和一个绕z轴旋转的力矩荷载h1eiwFt(属于平面外荷载)，所以在作用于轨头的横向荷载作用下，钢轨将产生平面内和平面外运动，而竖向荷载则只产生平面外运动。根据曲线Timoshenko梁理论，平面外与平面内运动方程是解耦的，式(1)～(3)为频域内曲线轨道的平面内运动方程[27-28]，分别表示为x轴和z轴方向的平移运动，以及绕y轴的扭转运动。

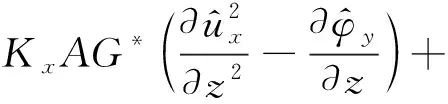
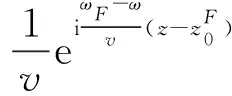
(1)

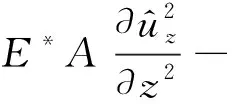
(2)

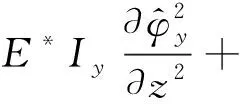
(3)

式(4)～(6)为频域内曲线轨道的平面外运动方程[28-29]，分别表示为y轴方向的平移运动，以及绕x轴和z轴的扭转运动。

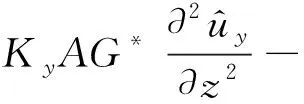
(4)

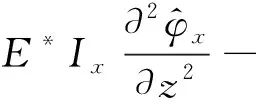
(5)

(6)

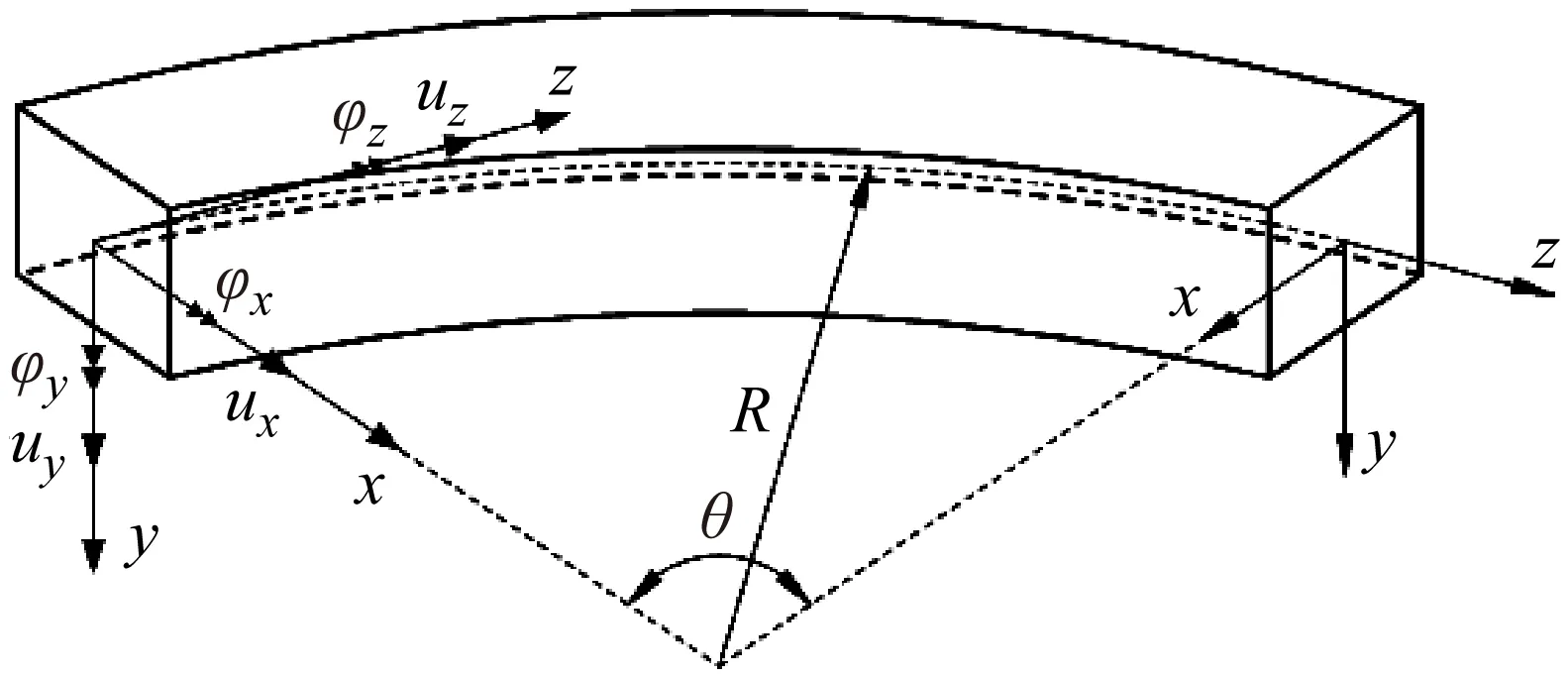
图1 曲线梁坐标系示意图

由于轨道结构在z轴上可以看作是周期性结构，所以可以将周期性结构理论应用于轨道的运动方程。设无限长的周期性轨道由无限个元组成，每个元都具有相同的性质，任意选择其中一个元作为基本元，则在移动谐振荷载作用下基本元的位移与其他元的位移具有如下的关系[30-31]：

(7)

(8)

把式(7)代入式(8)，可以得到：

(9)

(10)

式中：ξn=2πn/L，C=(Ux,Φy,Uz,Φx,Uy,Φz)T。则钢轨的位移可以写成：

(11)

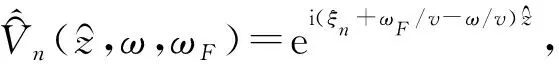
式(11)可以考虑有限个模态函数，设考虑2N+1个模态函数，并令κ=(ω-ωF)/v，则钢轨位移可以写成：

(12)

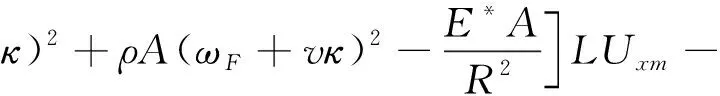
(13)

ρA(ωF+vκ)2-KxAG*-E*A(ξm-κ)2LUzm-

(14)

ρIy(ωF+vκ)2-KxAG*-E*Iy(ξm-κ)2LΦym+

(15)

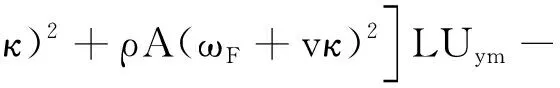
(16)

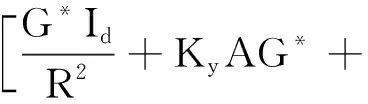
iKyAG*(ξm-κ)LUym=0

(17)

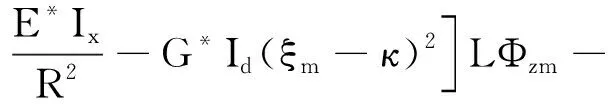
(18)

式中，

(19)

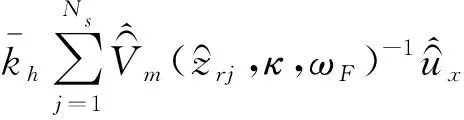
kh·V︵^-N(z︵r1)-1V︵^-N(z︵r2)-1…V︵^-N(z︵rNs)-1V︵^-N+1(z︵r1)-1V︵^-N+1(z︵r2)-1…V︵^-N+1(z︵rNs)-1︙︙…︙V︵^+N(z︵r1)-1V︵^+N(z︵r2)-1...V︵^+N(z︵rNs)-1V︵^-N(z︵r1)V︵^-N+1(z︵r1)...V︵^+N(z︵r1)V︵^-N(z︵r2)V︵^-N+1(z︵r2)…V︵^+N(z︵r2)︙︙…︙V︵^-N(z︵rNs)V︵^-N+1(z︵rNs)…V︵^+N(z︵rNs)Ux-N Ux(-N+1)︙Ux(+N)(20)同理可以计算式(16)和(18)中kv∑Nsj=1V︵^m(z︵rj,κ,ωF)-1V︵^y、kr∑Nsj=1V︵^m(z︵rj,κ,ωF)-1φ︵^z。式(13)～(15)可以归纳为:K︵in(κ,ωF)Uin(κ,ωF)=F︵^in(κ,ωF)(21)式中Uin(κ,ωF)={Ux(-N),…,Ux(+N),Φy(-N),…,Φy(+N),Uz(-N),…,Uz(+M)}T,K︵in(κ,ωF)为广义刚度矩阵,F︵^in(κ,ωF)为外荷载向量,同理,平面外运动可表示为:K︵out(κ,ωF)Uout(κ,ωF)=F︵^out(κ,ωF)(22)式中Uout(κ,ωF)={Uy(-N),…,Uy(+N),Φx(-N),…,Φx(+N),Φz(-N),…,Φz(+N)}T,外荷载向量可以表示为:F︵^in(κ,ωF)=F'inLeiκz︵〛F0/vF︵^out(κ,ωF)=F'outLeiκz︵F0/v (23)这里,F'in的第j个元素为:F'in(j)=1,0,(j=N+1)(j=其他) (24)F'out的第j个元素为:F'out(j)=1,h1,0,j=N+1j=5N+3j=其他(25) 钢轨上任意一点的动力响应为: u^in(z,κ,ωF)=ei-ncκLB(z,κ,ωF)K︵in(κ,ωF)-1F︵^in(κ,ωF)(26) u^out(z,κ,ωF)=ei-ncκLB(z,κ,ωF)K︵out(κ,ωF)-1F︵^out(κ,ωF)(27)式中为B(z,κ,ωF)模态矩阵。通过Fourier变换,时域内钢轨上任一点的位移为:u(z,t,ωF)=12π∫+∞-∞u^(z,ω,ωF) eiωtdω=12π∫+∞-∞u^(z,κ,ωF) ei(ωF+vκ)tvdκ= 12π∫+∞-∞Le-iκ(ncL-zF0)B(z,κ,ωF)K︵(κ,ωF)-1F' eivκtdκ eiωFt(28) 令式(28)中的v=0,则由固定谐振荷载引起的钢轨上的位移为: u(z,t,ωF)= 12π∫+∞-∞Le-iκ(ncL-zF0)B(z,κ,ωF)×K︵(κ,ωF)-1F' dκ eiωFt(29) 式(28)和(29)中,K︵(κ,ωF)可以是K︵in(κ,ωF)或者K︵out(κ,ωF),F'可以是F'in或者F'out。2 钢轨振动衰减率的计算根据欧洲标准BS EN 15461∶2008+A1∶2010进行[4],钢轨振动衰减率的计算公式如下:DR≈4.343∑nmaxn=0A(xn)2A(x0)2Δxn(30)