高频正弦压力发生装置的非理想因素影响分析

薛 斌， 杨 军，2， 李 博

(1. 北京长城计量测试技术研究所重点实验室， 北京 100095； 2. 北京航空航天大学 仪器与光电工程学院， 北京 100191)

随着我国新型武器装置的研制，动态压力测量的场合和需求越来越广泛，对高频动态压力高精度测量与校准的需求尤为突出。而且实际工程测试精度要求越来越高，不再满足于压力测试系统动态性能的定性评价，基于正弦压力校准的定量评价需求越来越显著。航空发动机研制试验中，对于涡扇发动机，最高转速可达18 000 r/min，压气机叶片数目最高可达100片，旋转时产生的脉动压力频率最高可达30 kHz[1]。叶轮机械叶片故障的叶间动态压力诊断法中，需要对积垢或扭曲等非正常状态下的转频谐波压力进行测量，比较明显的谐波成分最高达到18 kHz以上[2]。火箭发动机燃烧室内不稳定燃烧的压力脉动频率也可以达到20 kHz[3]，包括爆炸终极波超压测试过程中的测量系统固有频率也至少有100 kHz[4]。

在高频压力中，正弦周期性动态压力最为常见，针对高频正弦动态压力的发生以及动态测量问题，近些年来国内外取得了很大程度的突破。Lokar等[5]提出了使用双扬声器激振密闭腔空气产生最高700 Hz的正弦压力脉动，幅值可达到几十kPa。Kutin等[6]对该装置的模型进行了进一步完善，把校准频率提高到1 000 Hz，测试分析了校准压力腔中的压力发布一致性。Svete等[7-8]通过动力学分析建模，提出在振动台激励活塞式正弦压力发生器上采用双腔结构，从而提高振动系统动态输出位移，最终提高正弦压力幅值。在国内，陶继增等[9]利用压电换能器作为激励源，在谐振管内产生超过10 kHz的高频正弦压力脉动。针对谐振峰值辨识度问题，杨凡等[10]通过建立BP神经网络模型有效提高了模型精度与效率。目前针对实验室内所使用的高频动态压力发生装置，受到因管腔效应以及声固耦合等因素影响存在一定校准偏差，因此通过多物理场耦合仿真的方式，进行研究。目前针对多物理场耦合问题，COMSOL是近年来针对边界强耦合问题的仿真平台[11]，可以很好解决管腔内压力场与管壁结构场之间的耦合作用，从而让仿真结果根据有实验指导意义。

1 管腔压力理论

高频高压压力发生器利用液压管道受激谐振的原理，给安装在液压管道底部的压电叠堆施加交流电压，由于压电叠堆具有逆压电效应，在其表面会产生和激励电压频率一致的振动位移，这个位移迫使液体介质中产生传递的相同频率的压力波，当激励频率与液压谐振腔的谐振频率一致时，整个谐振腔发生谐振，从而在管道一端得到较大幅值的正弦压力波。整个结构模型，如图1所示。

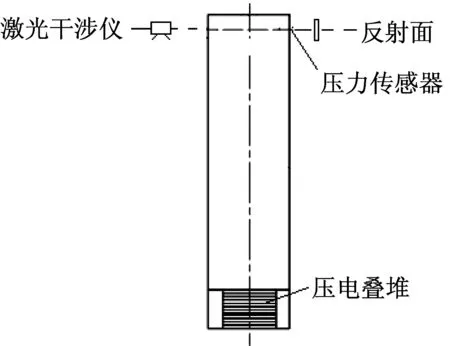
图1 高频正弦压力换能器发生装置

通过在顶端安装压力传感器以及激光干涉仪进行动态压力的测量以及校准。

1.1 压电谐振理论分析

向压电叠堆施加一定幅值的交流信号时，压电堆表面就会出现位移，此时即可等效为高频振动源，若施加的交流信号为：

V(t)=Vmsin(2πft)

(1)

式中：Vm为电压幅值；f是电压频率。因此可以得到压电表面产生的振动位移为：

X(t)=nd33δE=nd33V(t)=nd33Vmsin(2πft)

(2)

式中：X(t)是总振动位移；n和δ分别为压电片的层数和单片厚度；E为压电叠堆极化方向电场强度；d33为压电材料纵向逆压电系数。

对位移求导，可以得到施加速度表达式为：

v(t)=nd33Vm2πfsin(2πft)

(3)

可知速度的规律模式与位移的相同，流体管腔的动态特性和流体的压缩性及质量有关，这二者的关系与管内压力波速有关，当叠堆表面(等效为活塞)以速度v(t)振动时，在极短的时间Δt内其右边的介质受到压缩，密度和压力分别变化Δρ和Δp，这些信息将在管道内以比v(t)大得多的速度a0传播，根据流体传输连续性方程：

ρAv(t)Δt=ΔρA(a0-v)Δt

(4)

液体的体积弹性模量为：

(5)

当认为声速远大于振动表面的速度时，联立上式：

(6)

即：

(7)

因此可以知道，换能器上表面对液体产生的扰动压力也按正弦规律变化。持续的激励使得这个压力波在封闭的管腔内多次反射形成驻波，当激励频率和管腔的谐振频率一致时管腔产生谐振，此时在管腔的一端将达到较大的压力幅值，就形成了正弦波。

1.2 管腔谐振理论分析

根据管道的谐振原理能够使压力发生器得到较大幅值，通过建立谐振腔的数学模型并分析其谐振条件，可以为压力发生器的设计参数提供理论依据。

根据流体传输管道动力学，流体传输管道的动态特性基本方程为[12]：

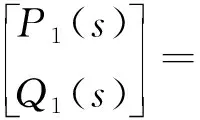
(8)

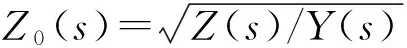
(9)

在管腔长度为L时，发生谐振的频率可以等效为：

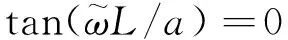
(10)

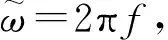
(11)

可知在管腔内部选择介质为水时，压力波在水中的传播速度在常温下为1 480 m/s，因此对于长度为0.74 m的管腔，其基频为1 kHz，谐振点的分布则为基频的整数倍。

2 压力管腔仿真模型

对于高频正弦压力发生装置的仿真要分析管腔内的压力场与管壁结构场之间的耦合作用，因此采用COMSOL多物理场耦合分析软件，建立二维轴对称模型进行仿真研究。

2.1 管腔模型建立

为了对比纯压力场和压固耦合场的区别，以及与实验装置相比较，分别建立单一压力场模型以及与管壁之间存在耦合作用的做物理场模型。

管腔内的压力场尺寸为内径90 mm，长度740 mm，顶端安装压力传感器的位置大小为5 mm的小管腔，同时利用激光干涉法进行动态压力测量，实现与压力传感器的对比分析。在考虑压固耦合的模型中，与实验模型相同，管壁厚度为30 mm，顶端端盖位置处的壁厚为20 mm，两种模型的网格划分均采用三角形网格，在管腔连接位置进行加密处理，曲率因子为0.25。划分结果,如图2所示。

图2 纯压力场和多物理场的模型网格划分

在材料选择上，认为管腔内部充满水介质，管壁材料选择结构钢，且整个过程不考虑与外界的热交换。

2.2 管腔边界条件

在考虑结构场与压力场之间的相互耦合作用时，水域压力场的变化将会导致结构场发生形变，而固体受到正弦压力的作用也会因应变而产生应力，反作用与水域流场中，因此这部分耦合作用在实际实验当中不能忽略。通过COMSOL中的耦合边界条件方程，满足在接触面的外侧方程为[13]：

(12)

而在水域声场的内侧，则满足方程：

(13)

(14)

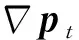
2.3 管腔仿真结果对比

对上述两种模型进行仿真对比，初始管腔内加压至1 MPa，根据理论分析，向管腔内施加正弦压力速度时，对介质即施加正弦动态压力，频率为1 kHz，加速度幅值为1 mm/s2。因此，在底端施满足正弦加速度激励时，两种不同模型的谐振点分布,如图3、4所示。

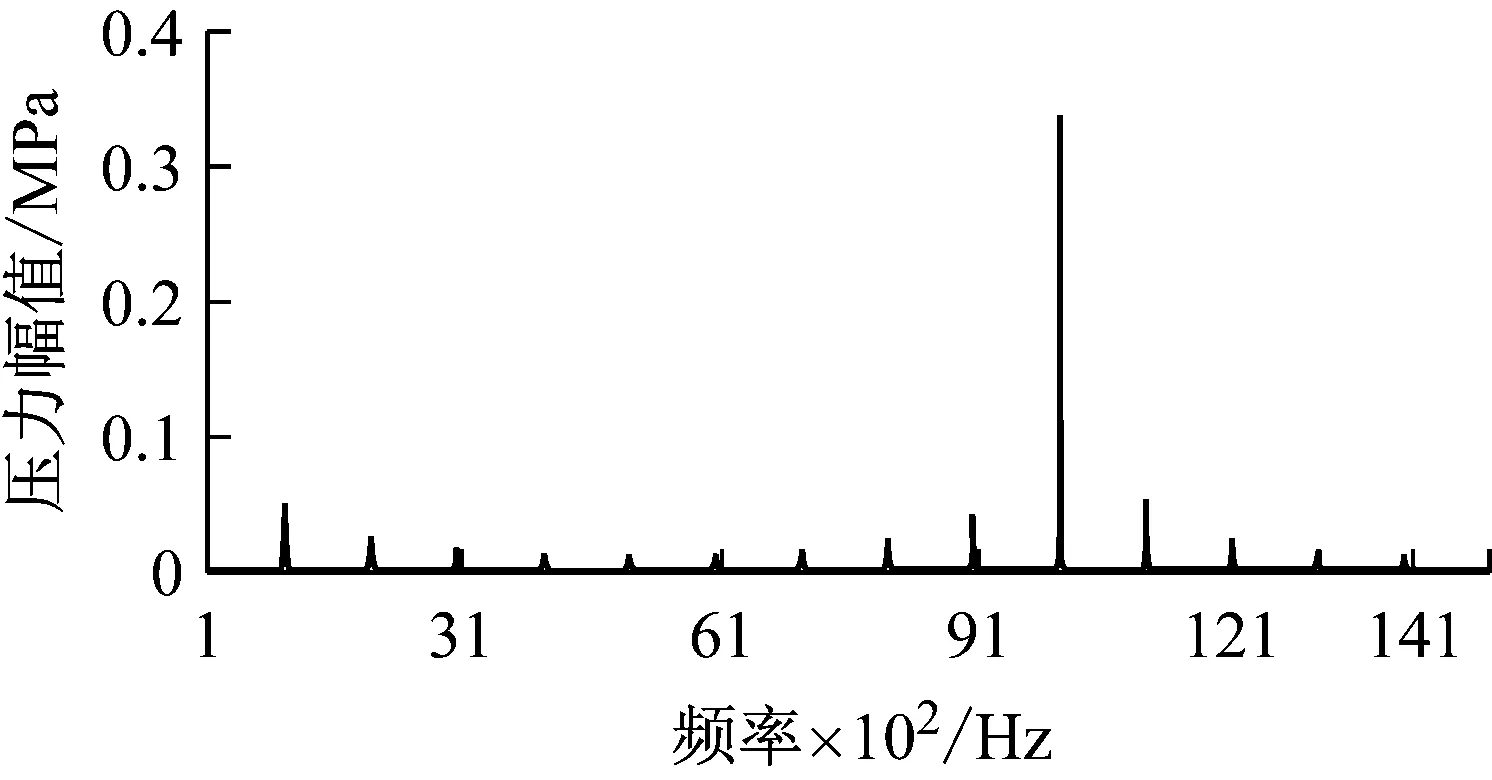
图3 纯压力场下的谐振点分布情况

根据二分之一波长计算公式，纯压力场时，在低频段压力幅值在0.01 MPa量级。管腔内的谐振幅值在水介质影响下，在10 kHz时出现频率段的峰值。

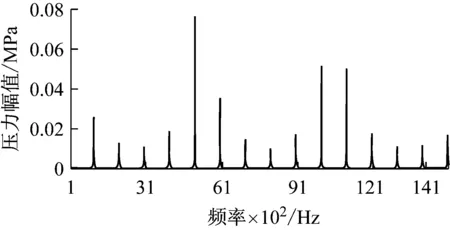
图4 压固耦合场情况下谐振点分布情况

在考虑压固耦合的情况下，管腔内的谐振幅值将会受到管壁形变的影响。在正弦动态压力的作用下，水介质的径向尺寸会发生形变，同时压力场的能量在使得管腔形变中出现能量损失，因此会导致谐振幅值相对于纯压力场低很多。

通过对比两种情况的谐振点分布，可以看出，纯压力场时谐振频率基本与理论值，即1 kHz的整数倍相吻合，而压固耦合的情况在10 kHz频率以下时谐振点一致，在10 kHz及以上时，谐振频率存在20 Hz的偏差。压力幅值上，纯压力场在低频段明显幅值高于压固耦合情况，在高频部分幅值差距较小。实际过程中应基于耦合情况进行研究，而不同频率谐振点位置处管腔压力分布，如图5所示。

(a) 谐振频率1 kHz时压力分布

(b) 谐振频率5 kHz时压力分布

(c) 谐振频率9.98 kHz时压力分布

(d) 谐振频率14.8 kHz时压力分布

通过压力云图可以看出，在频率为1 kHz时，管腔内此时为一个周期的压力分布，出现明显一次波峰波谷。随着频率增加，在n倍基频附近都会出现n个压力分布的波峰波谷，与理论值相符。可以看出随着谐振频率的增大，管腔内的压力波峰越多，与理论分析的结果相一致。

3 不同压力管腔设计仿真分析

在理想情况下，仿真结果与理论结果想接近，但是在实际安装过程中会存在一切偏差，因此基于管腔与管壁之间的耦合情况下，可以通过仿真验证实际实验中出现的偏差对管腔谐振点的影响。

3.1 安装缝隙的影响

在实际管腔安装过程中，整个压力腔由三段拼接组成，因此在实际中每一段管腔之间会存在工程缝隙，通过仿真的方式分析缝隙对谐振点分布以及幅值的影响大小。工程上的安装缝隙尺寸一般为深度4 mm，纵向1 mm，因此通过在管腔侧壁以及顶端在模型上设置缝隙，仿真模型结果，如图6所示。

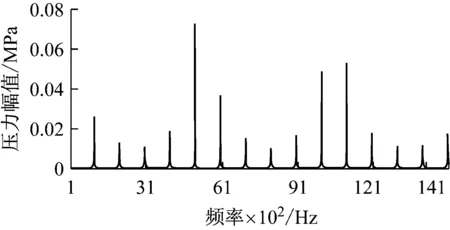
图6 考虑缝隙条件下管腔谐振分布情况

由于管腔之间的缝隙存在，导致管腔整体长度与理想值之间存在误差，因此会引起谐振频率的偏移。同时通过数据对比可知，安装缝隙对于谐振点的频率影响很小，对谐振点位置处的压力幅值有一定影响，具体数值如表1所示。

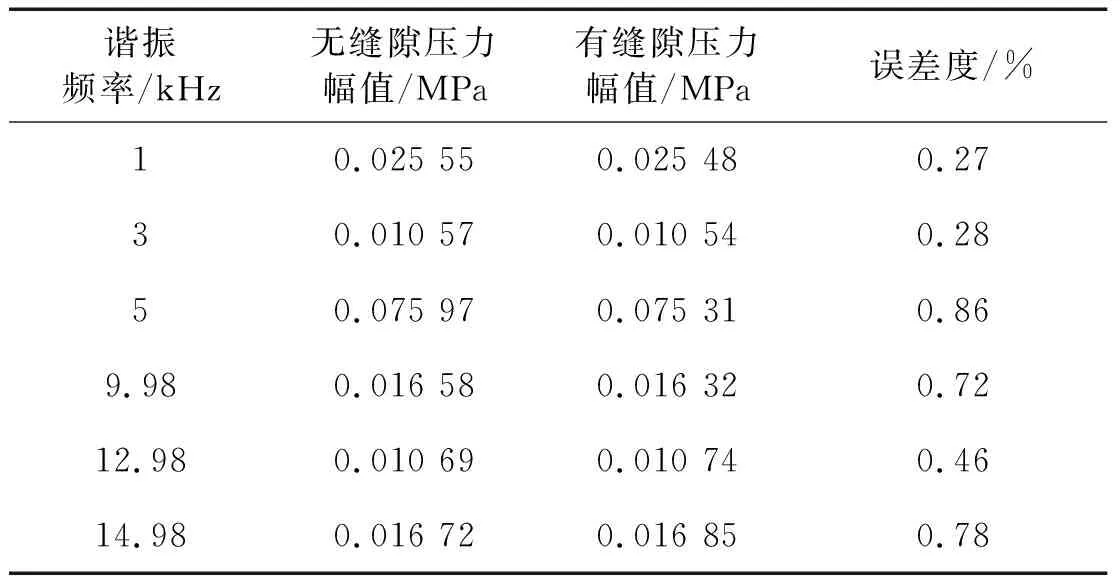
表1 安装缝隙对谐振点压力幅值影响对比

因此，在管壁材料采用结构钢时，由于泊松比较大，安装缝隙对谐振点频率几乎没有影响，在幅值方面，通过数据对比，可知工程上的误差度在1%以内。且在谐振频率低于10 kHz时，没有安装缝隙的幅值要高于存在有缝隙的情况，高频部分则相反。

在实际实验过程中，安装缝隙与人为影响因素较大，因此对缝隙不同宽度进行分析，取低频和高频两点进行分析，对比结果如图7所示。

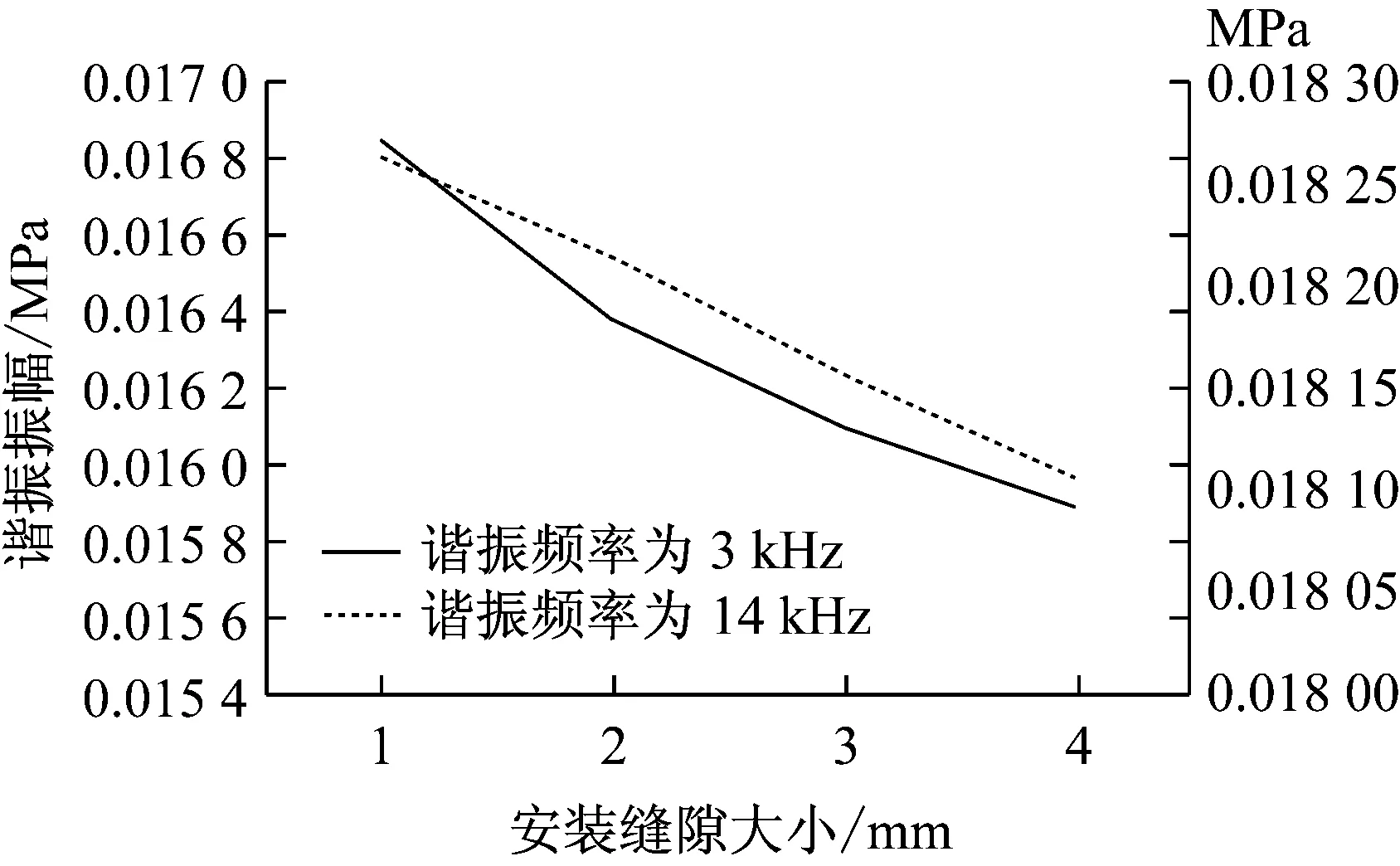
图7 谐振幅值随安装缝隙大小的变化关系

选取低频点3 kHz以及高频点14 kHz进行分析比较，可以看出随着安装缝隙尺寸的增加，对应的谐振频率处的压力幅值会随之降低。

3.2 底端面存在安装角度影响分析

管腔底部安装压电换能器时，很难保证振动面与管腔截面平行,因此在实际情况下，振动面与管腔径向方向存在一定的安装角，通过对不同安装角度进行仿真分析，可以得到对谐振频率分布和压力幅值的影响，如图8所示。

(a) (b) (c) (d)

图8 底部的安装角为5°时谐振频率为3.02 kHz，7.03 kHz，10.04 kHz，14,05 kHz下的压力分布

Fig.8 The pressure distribution of 2°installation angle at3.02 kHz，7.03 kHz，10.04 kHz，14,05 kHz

可以看出低频部分管腔内压力分布与理想情况较为一致，压力波的波峰波谷较为均匀。当频率较高，超过10 kHz时，在谐振频率下底部的安装角导致的误差则较为明显，压力分布不再均匀，而是受到角度影响呈现一定反射规律，压力幅值也随之变化。在安装角度达到5°时，管腔内的谐振频率分布，如图9所示。

图9 安装角达到5°时管腔内的谐振频率分布情况

由于存在安装角度，振动面形成的压力波会在管腔内发生反射，从而会使得一些谐振频率点出现偏移。随着频率增加，波峰波谷分布密集，反射影响严重，压力峰值不再完全呈现径向分布，反射的压力波对管壁作用明显，使低频段一些谐振频率点处幅值增大。

安装角度不同时，对管腔内的谐振频率以及压力幅值的影响存在差异。在工程安装中，受到管腔长度影响，绝对安装角度可以控制在5°范围内。分别针对安装角为1°，2°，3°，4°以及5°的情况进行仿真分析并对比。对应谐振点位置处的频率出现了一定程度的偏移，并不完全满足1 kHz的整数倍，安装角度以及对应谐振频率的具体关系，如表2所示。

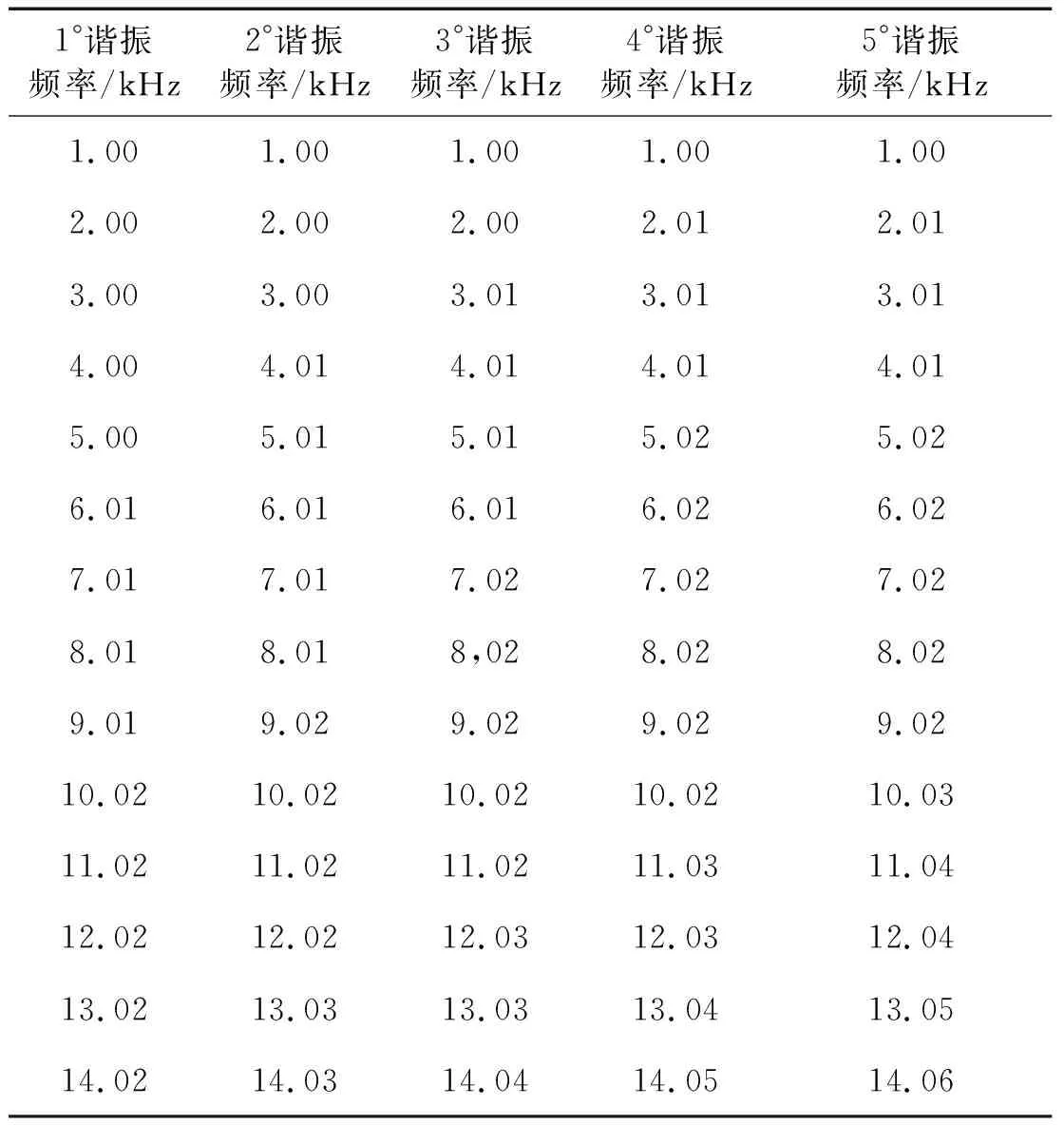
表2 不同安装角下管腔的谐振频率

通过上表可以看出，管腔底部压电换能装置的安装角度对谐振频率有一定的影响，随着安装角度的增加，谐振频率与理论值的偏差越大，且对高频部分影响严重。因此在进行高频正弦压力的实验分析过程中，应尽量降低安装过程中因为偏差导致的安装角。

3.3 管腔内存在空气时影响

在实验时，管腔内注满水介质，并加压至1 MPa作为初始压力。而在加压很小时，管腔内水介质在实际过程中难以充满整个管腔，与顶端压力会存在很薄的空气夹层，由于介质影响音速，进而影响压力在管腔内的传播，因此通过仿真的方式可以得出空气层对管腔谐振压力的影响，如认为管腔顶端存在1 mm的空气夹层，则管腔的谐振点频率分布以及压力幅值情况，如图10所示。

通过谐振点分析可知，在有空气夹层时，谐振点位置处的压力幅值相比较无夹层情况明显降低，尤其对低频情况下影响较为严重，如图11所示。

除基频整数外，由于管腔效应的影响，此时在频率为4 560 Hz时出现谐振。因此在实验过程中应尽可能排尽管腔内的空气，减小对谐振幅值以及谐振频率的影响。

4 管腔实验结果分析

针对管腔设计的尺寸进行了实验。过程中采用48层封装的压电叠堆，应变放大器选择CDV-700A，顶端安置的压力传感器型号为CYG0401Y，量程6 MPa，满足实验要求，信号发生器为Agilent 33220A，功率放大器为SINOCERA YE5872。搭建的实验结构，如图12所示。

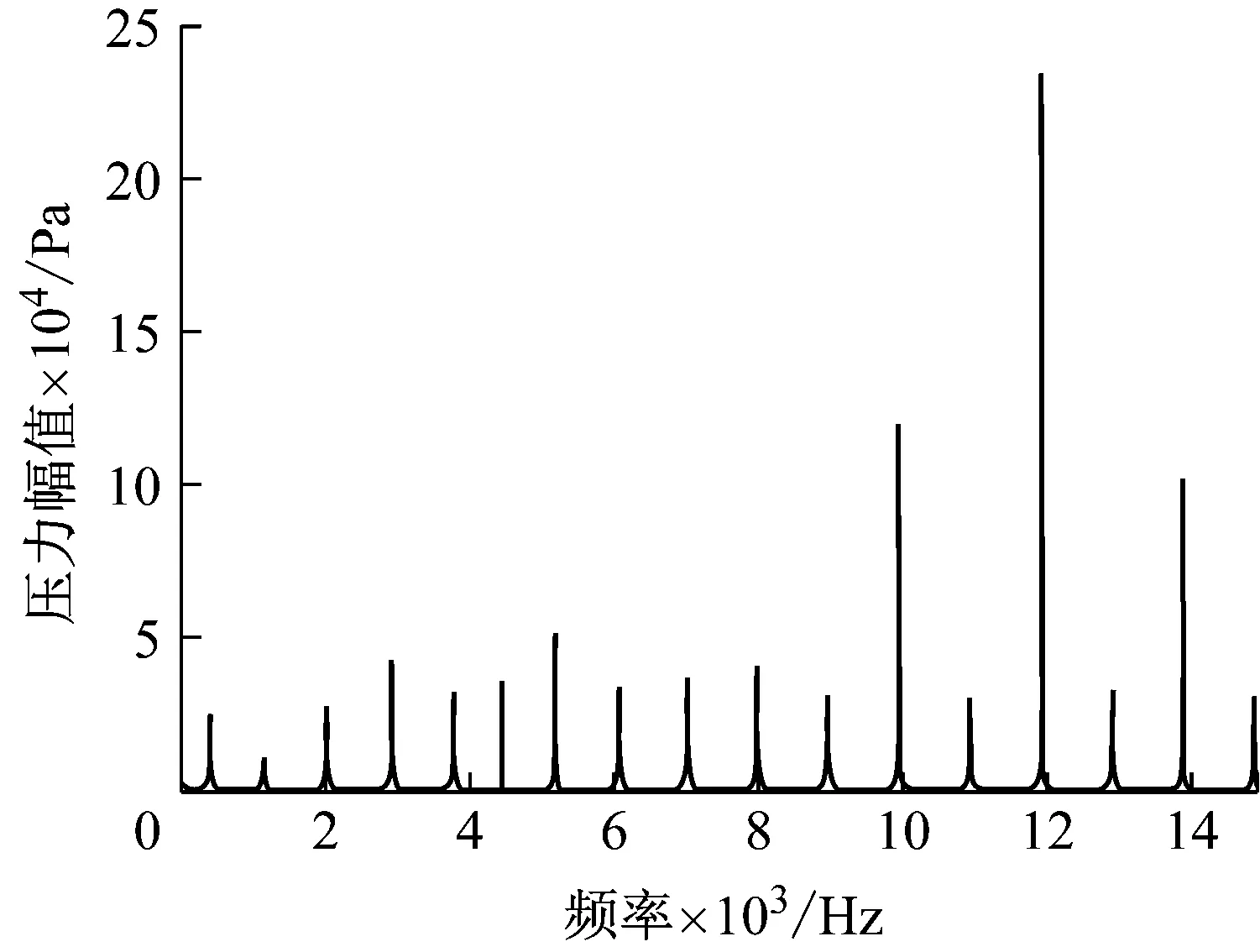
图10 存在空气夹层条件下谐振频率分布情况

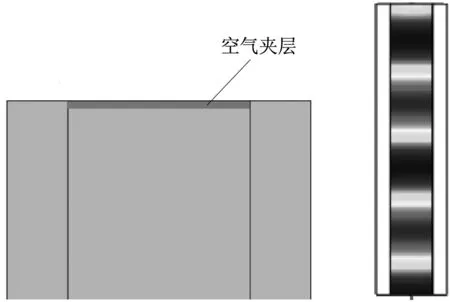
图11 空气夹层模型以及谐振频率为4 560 Hz时压力分布

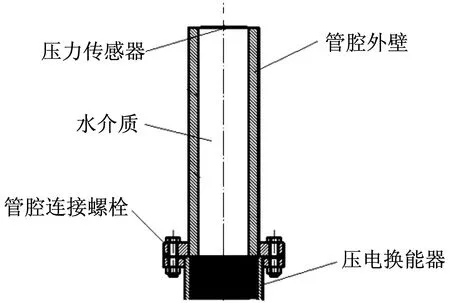
图12 实验采用的管腔设计结构

通过下面的压电叠堆，向管腔内施加周期性正弦压力，得到的输入波形，如图13所示。

通过实验采集到的压力波形可知，通过压电堆叠装置输入满足正弦压力，且失真度较小。根据顶端安置的压力传感器进行监测，可以得到管腔内的谐振点分布情况，如图14所示。

可以看出在实际实验中，由于工程误差造成的安装缝隙问题对高频段产生的影响较大，幅值明显变低，同时谐振频率点低于理论值，与仿真结果趋势相同。

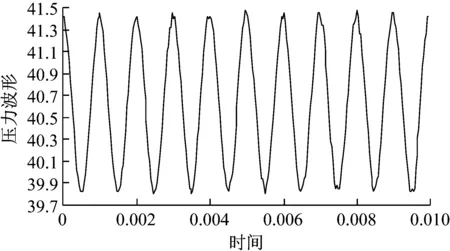
图13 实验过程中的压力输入波形

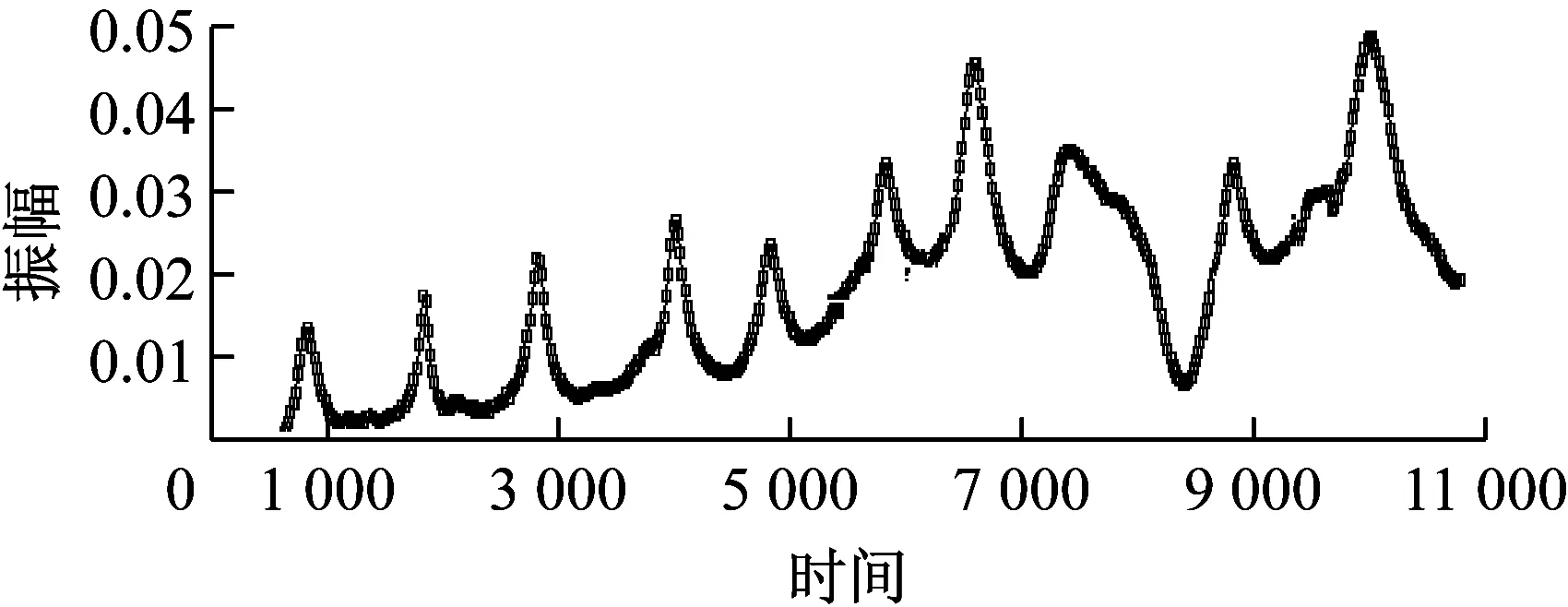
图14 直筒设计低频段0～10 kHz时管腔谐振频率分布

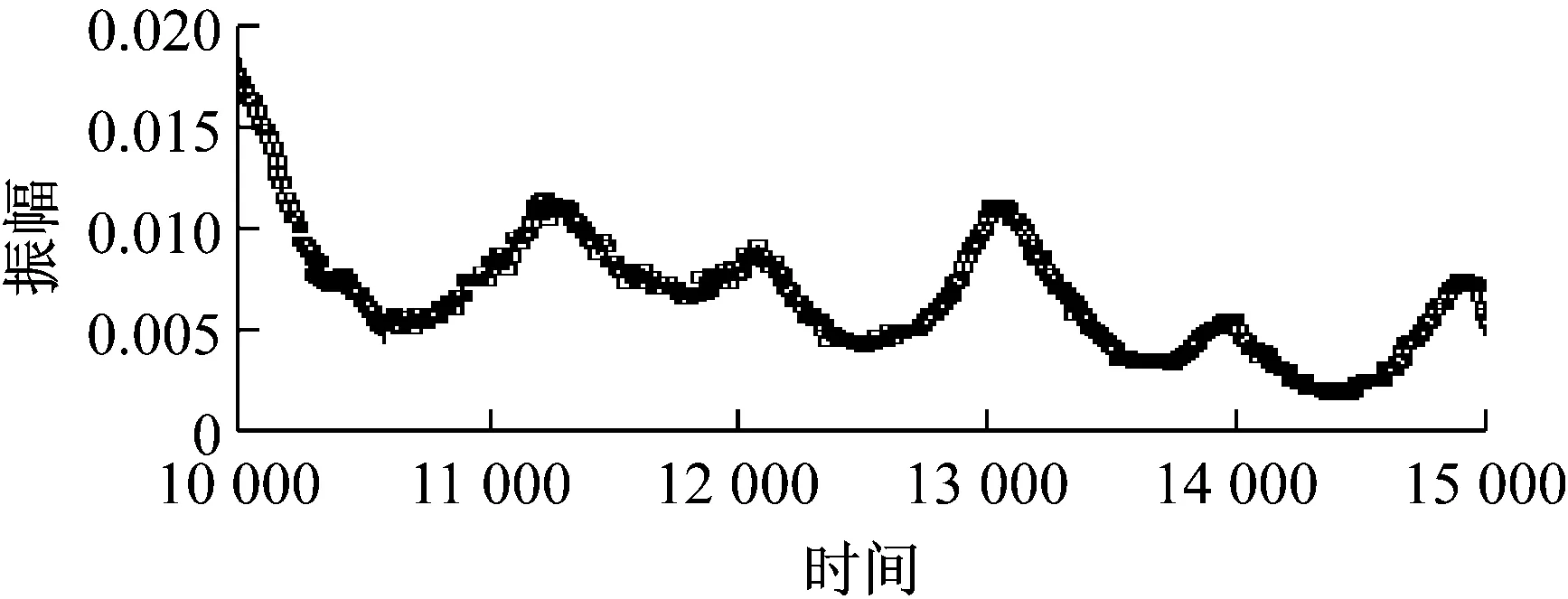
图15 直筒设计时10～15kHz时管腔谐振频率分布

在实验过程中，为了排尽管腔内空气，需要加满水后进行加压处理，上一组实验施加了1 MPa的静压，保证排尽了管腔内空气，在加压为0.4 MPa时会出现空气残留，此时进行实验，结果如图16和17所示。

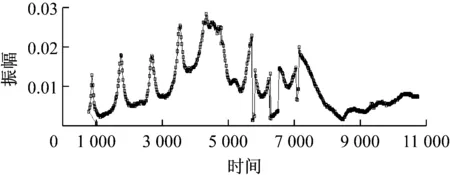
图16 有空气层时0～10 kHz时管腔谐振频率分布

通过实验对比，可知在初压较小时容易导致管腔内有空气层，对谐振点的影响主要为压力幅值的下降。并且在低频部分会出现其他谐振峰值，主要为空气层由于介质改变使得压力波传播音速变化，从而出现理论值以外的谐振频率。经过多次实验，重复性较高，且实验结果的变化趋势与仿真情况基本一致。

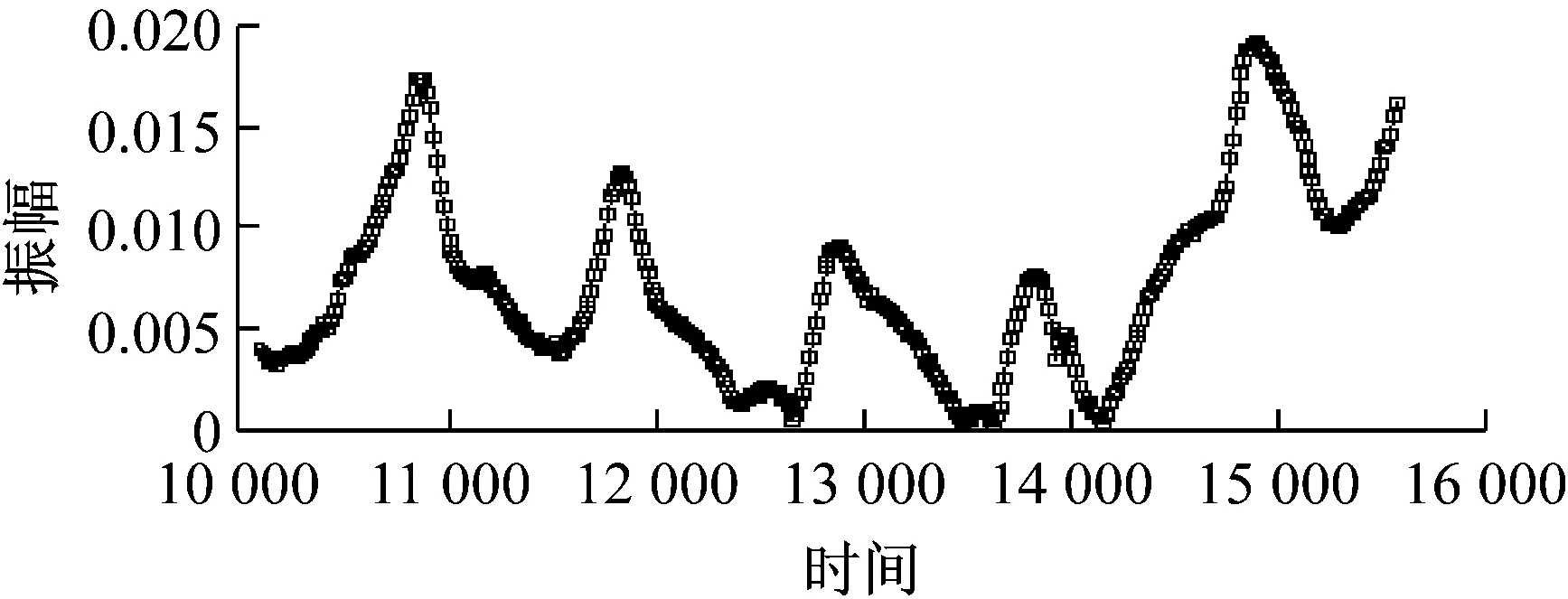
图17 有空气层时10～15 kHz时管腔谐振频率分布

5 结 论

通过对高频正弦压力发生装置进行理论计算以及仿真分析，可知纯压力场的模型下结果与理论分析结果相一致，管腔模内选择水介质时，利用二分之一波长公式可知在管腔长度为0.74 m 时谐振点分布为1 kHz的整数倍，但是实际过程中会存在压力场与管壁结构场之间的耦合作用，通过仿真结论可知，耦合作用导致在低频段10 kHz以内的谐振频率偏移量在2‰以内，超过10 kHz时，偏移误差度则超过了2‰。

针对工程安装问题产生的非理想因素进行研究，可知管腔安装出现缝隙时，随着缝隙的增大，谐振点处的压力幅值越小。根据仿真结果可知，工程上1 mm的安装缝隙造成的误差度在1%以内，超过3 mm时误差度已经达到了5%以上，因此应尽量减小工程安装偏差。压电换能器作为激励源时，当出现安装角时将会使得谐振频率出现偏移。仿真结果表明，对于目前设计的管腔长度与结构安装，安装角可以控制在5°范围内，随着角度的增加，高频段影响严重，在谐振频率超过10 kHz时，偏移误差达到了4‰，因此安装过程应尽量保证振动面与管腔径向截面垂直。当管腔内水介质与管腔顶部存在空气层时，根据仿真与实验结果可知，在存在1 mm的空气夹层时，顶端安装方式对谐振点压力幅值影响严重，高频段误差度在1%左右，低频段则达到了3%，因此应采用加压的方式尽可能防止空气残留。实验数据对仿真以及理论结果进行验证，非理想因素导致的误差趋势相同。