7075-T651铝合金靶板剪切冲塞的试验和数值模拟研究

肖新科， 陈 琳,2， 杜太生,2

(1.南阳理工学院 土木工程学院，河南 南阳 473004；2.郑州大学 土木工程学院，郑州 450001)

铝合金由于价格低廉、比强度高、承载能力良好以及易于加工等优点仍广泛应用于军民用防护体系中[1-2]。亚弹速范围内，金属板材的抗侵彻性能与其破坏模式密切相关[3-5]。刚性平头弹撞击厚度接近弹体直径的靶板时，靶板通常发生剪切冲塞破坏[6-7]。在剪切冲塞过程中，靶板不同区域的材料由于弹体的撞击而产生速度差，特别是弹体头部下方的靶板材料和其他区域的材料之间。这就在弹体头部直径附近非常窄的环状靶板材料中产生非常局部化的剪切变形。由于加载在极短时间内完成，塑性变形产生的热量来不及传导给周围的介质，因此这种剪切冲塞也常称为绝热剪切冲塞[8]。剪切冲塞所涉及的问题十分复杂，如应变硬化、应变率硬/软化、局部温升、温度软化、损伤的累积演化甚至软化、裂纹的起裂和扩展等。因此，对涉及剪切冲塞的分析往往需要借助有限元等数值计算方法。

公开文献中尽管有一些涉及剪切冲塞的成功的数值模拟报道[6-9]，但仍有报道显示数值模拟无法对弹道极限给出合理的预报，如Børvik团队的报道[10-11]。 特别地，Dolinski等[12]甚至认为目前对弹道过程中的失效行为进行数值预报的水平仍旧处于起步阶段。因此，对涉及剪切冲塞在内的弹道行为的数值预报仍需进一步研究。

Teng等[13]在评价6个断裂准则在高速侵彻弹道行为数值预报中的应用时发现，剪切冲塞裂纹路径上应力状态接近于平面应变，即Lode参数ξ=0。这种应力状态与圆棒拉伸试验中的应力状态(ξ=1)截然不同。但是对弹道行为进行数值模拟时采用的断裂准则通常都是通过圆棒拉伸试验进行标定，如文献[14-15]等。

目前的试验和数值模拟等表明不少金属材料的断裂除了与应力三轴度有关外，还与Lode角/参数有关[16-19]，特别是在低值应力三轴度区间。这些研究表明，材料在平面应变这种应力状态下(ξ=0)的断裂应变要小于单向拉伸(ξ=1)或者双向拉伸(ξ=-1)时的。因此如果基于单向拉伸试验标定断裂准则并应用于冲塞剪切相关的弹道行为的数值预报时必然会高估材料的延性，并最终导致不合理的数值预报结果。

本文首先开展材料性能测试，标定本构模型和断裂准则；接着使用平头刚性弹体开展打靶试验，获得弹道极限和靶板的失效行为；然后分别使用Lode相关和无关的断裂准则开展数值打靶试验，获得两种断裂准则的预报结果，通过与试验结果的对比揭示Lode相关断裂准则在剪切冲塞数值模拟中的必要性。最后，通过应力状态的分析揭示Lode参数相关断裂准则影响数值预报结果的原因。

1 7075-T651本构模型和断裂准则

1.1 7075-T651材料本构模型及断裂模型

本构模型拟采用Johnson-Cook 本构模型[20](JC模型)，Von Mises等效应力写为

(1)

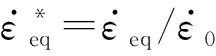
Johnson-Cook断裂准则[21](JC准则)考虑了应力三轴度、应变率和温度的影响，广泛应用于冲击相关的数值计算中，断裂应变写为

εf=[D1+D2exp(D3σ*)]×

(2)

式中：D1-D5为模型参数；应力三轴度σ*=σm/σeq=(σ1+σ2+σ3)/(3σeq),其中σm、σ1、σ2和σ3依次为平均应力、第一、第二和第三主应力。

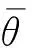
(3)

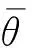
(4)

Wen等[22]提出了一个反映应力三轴度和Lode角影响的断裂准则，但该准则(WM)没有包含温度和应变率效应。借用J-C断裂准则的形式，在该断裂准则的表达式中加入温度和应变率效应，WM断裂准则最终表达为

(5)

式中：C7-C9为该准则的模型参数。

1.2 材料性能测试

为标定本构模型和断裂准则，开展了光滑和缺口圆棒的拉伸试验以及平板试样(如图1所示)的剪切试验。光滑圆棒标距段内以及缺口圆棒缺口处直径为6.0 mm，缺口半径包括R=2、3和9 mm。试验中采用标距为25 mm的引伸计跟踪了标距段或缺口段的伸长量，得到的载荷位移曲线如图2所示，拉断的试样如图3所示。

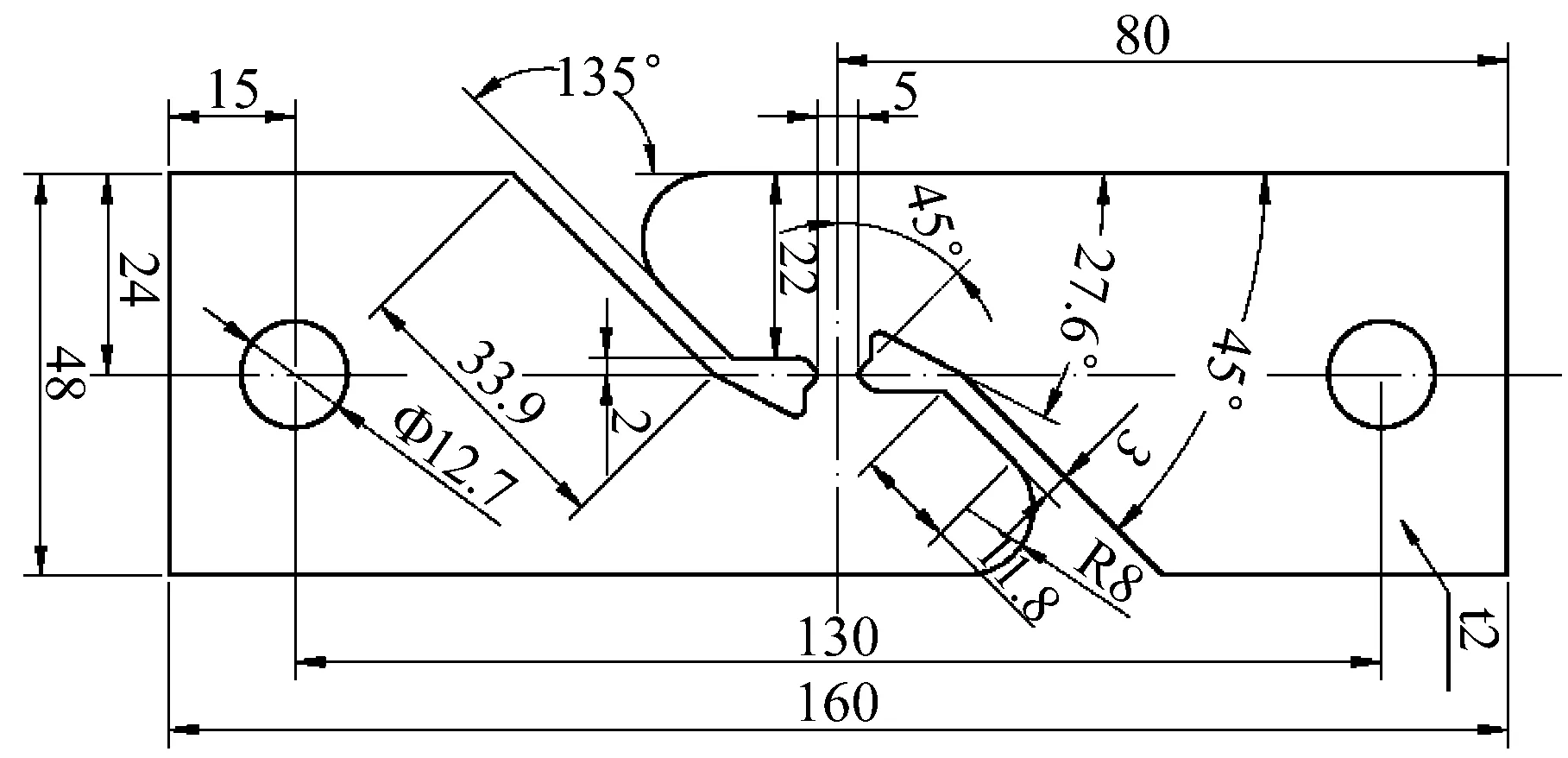
图1 剪切试样

在对剪切试样加载的过程中采用非接触式应变测试系统MatchID监控了试样表面的变形和应变演化情况，图4展示了断裂前试样中的等效应变分布情况。可见，剪切应力状态下断裂应变约为0.266。

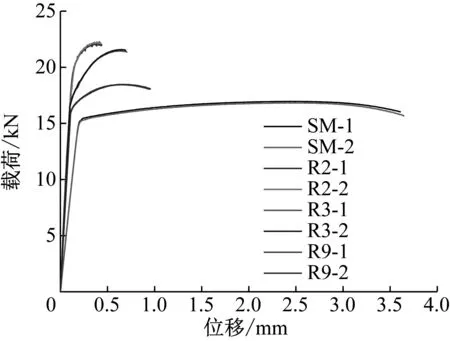
图2 光滑和缺口圆棒试样的载荷位移曲线

Fig.2 Lode-displacement curves for smooth and notched round bars

图3 断裂的光滑和缺口圆棒试样

Fig.3 Smooth and notched round bars under tension at fracture

图4 断裂前剪切试样的等效应变

1.3 本构模型和断裂准则模型参数的标定

由光滑圆棒拉伸试验的载荷位移曲线可换算得到工程应力-工程应变曲线，得到两个试验的平均屈服强度为546.9 MPa，即JC本构模型中的A=546.9 MPa。应变硬化参数B和n通过对光滑圆棒拉伸试验有限元计算的迭代优化得到，具体过程见文献[1]。迭代优化结果见表1。本文得到的A、B和n与文献[23]中的结果十分接近。由于没有开展SHPB试验和高温拉伸试验，C、m、D4和D5的取值参考文献[23]。7075-T651 的全部J-C本构参数,如表1所示。

单向拉伸试验中，断裂应变计算为εf=ln(A0/Af),其中为A0、Af分别为试样初始横截面积和拉断后的断口面积。通过测量试样的初始直径和断口直径获得了各试样的断裂应变，各试样中的应力三轴度可由Bridgman公式[24]获得，该公式写为

σ*=1/3+ln[1+a/(2R)]

(6)

表17075-T651铝合金材料模型参数

Tab.1Materialmodelconstantsfor7075-T651aluminumalloy

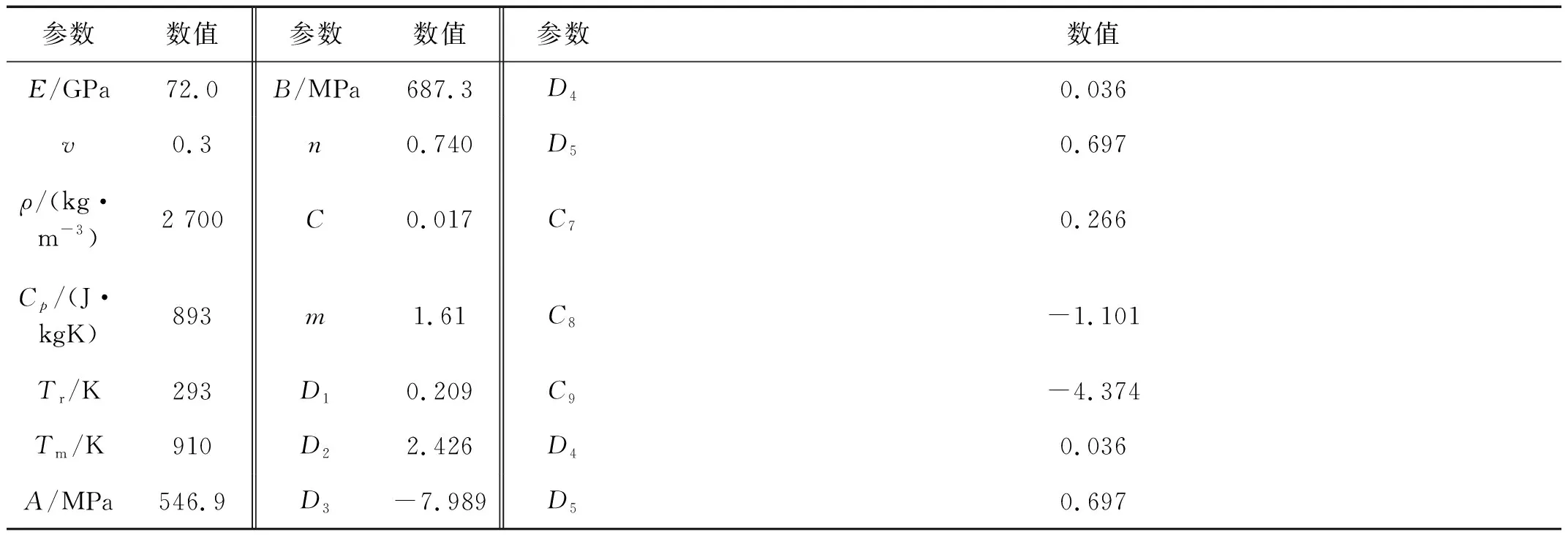
参数数值参数数值参数数值E/GPa72.0B/MPa687.3D40.036v0.3n0.740D50.697ρ/(kg·m-3)2 700C0.017C70.266Cp/(J·kgK)893m1.61C8-1.101Tr/K293D10.209C9-4.374Tm/K910D22.426D40.036A/MPa546.9D3-7.989D50.697

式中：a和R分别为缺口试样缺口处的半径和缺口半径。

表2 各应力状态下的断裂应变

利用表2中的数据可拟合出两个断裂准则中除应变率和温度效应的模型参数。由于JC准则通常由圆棒试样标定，因此拟合JC准则时没有考虑剪切试验数据。拟合得到的模型参数列于表1中，两个模型的预报效果,如图5所示。

可见，7075-T651铝合金的断裂应变与Lode角相关；仅考虑应力三轴度的JC断裂准则无法合理预报7075-T651铝合金的断裂应变；Lode相关的WM断裂准则可很好的预报其在各应力状态下的断裂应变。

2 7075-T651靶侵彻试验及数值模拟

2.1 实验概况

靶板材质为7075-T651铝合金，原材料为直径50.8 mm棒材，与材料性能测试原材料相同。圆形靶板的直径和厚度分别为50.8 mm和6 mm。靶板(如图6所示)通过11个M3的螺栓与靶架进行连接。

试验中的弹体为平头圆柱钢弹，名义直径、长度和质量分别为5.96 mm、29.82 mm和6.40 g，其硬度均值为54 HRC。

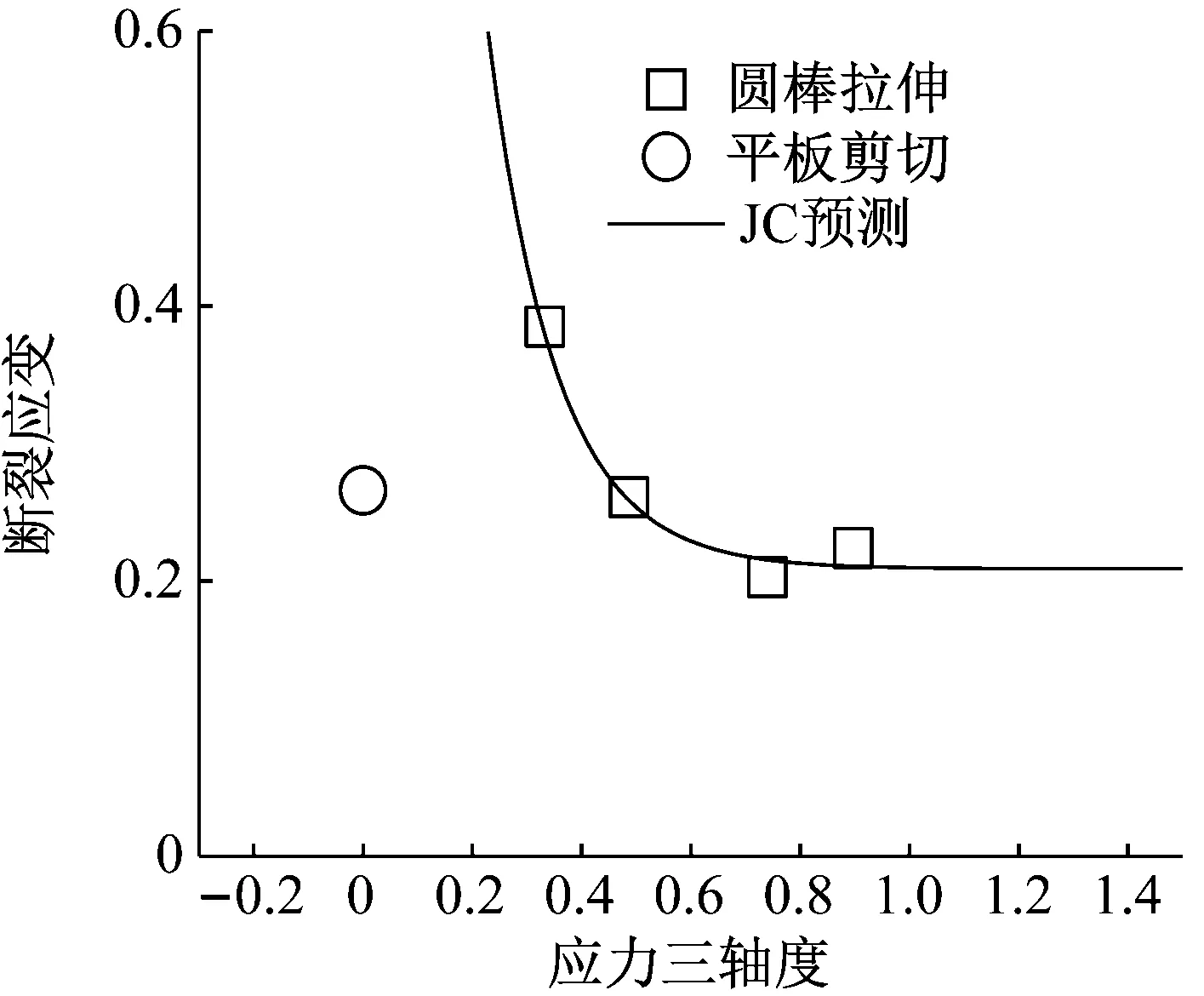
(a) Johnson-Cook

(b) Wen-Mahmoud

Fig.5 Fracture strain data and predictions of the two fracture criteria

图6 靶板和平头弹

撞击试验在南阳理工学院土木工程学院的一级轻气炮上完成，该试验装置的详情见文献[25]。试验过程中采用FASTCAM SAZ高速摄像机记录打靶过程。弹体的初始速度和剩余速度通过高速相机测得。弹体的初始撞击速度通过改变压缩气体的压力进行调节。

2.2 实验结果

试验的详细结果如表3所示。试验中弹体全长未穿过靶板或反弹时记剩余速度Vr=0。从表中可见弹道极限介于163.0～178.2 m/s之间。通过Recht[26]公式(R-I公式)可拟合得到弹道极限，R-I公式写作:

(7)

式中：a,p为模型参数，Vbl为弹道极限。这三个参数可通过最小二乘法拟合初始-剩余速度数据得到。拟合得到的最终结果为Vbl=163.0 m/s。

试验中子弹反弹和嵌入靶板的共有5发，其中1发试验(No13)初始速度较低,靶板产生冲坑和背部鼓包，子弹反弹。4发试验No15、No11、No9、No14，弹体初始速度在136.5～163.0 m/s之间，靶板被打穿，塞子飞出，但子弹嵌入靶板，如图7所示。

表37075-T651铝合金靶板的弹道试验结果

Tab.3Ballistictestresultsof7075-T651aluminiumalloyplates

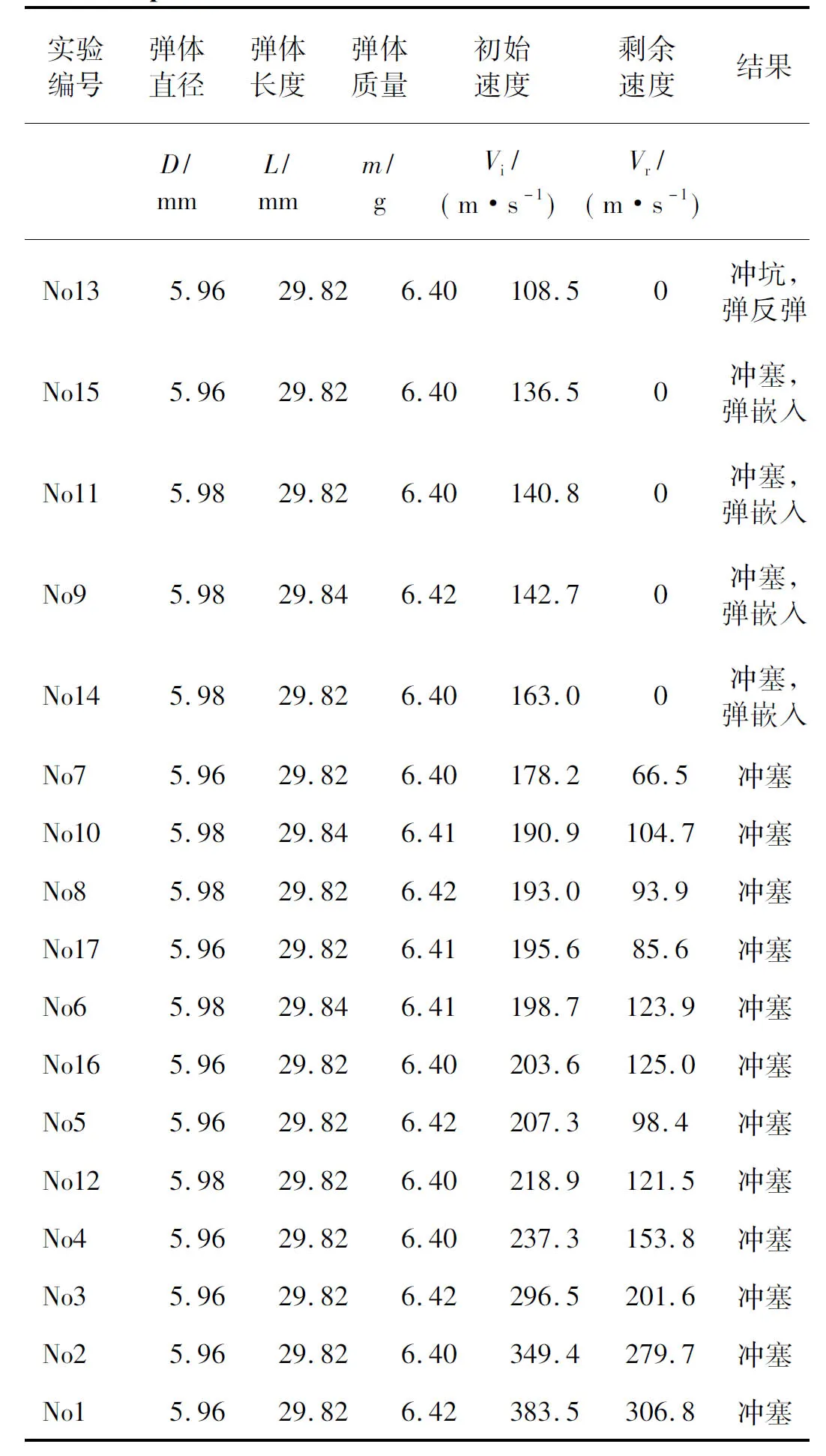
从表3可见，当子弹撞击靶板的初始速度Vi≥0.8Vbl时，弹体均发生剪切冲塞破坏。

当弹体初始速度高于弹道极限时，靶板发生冲塞破坏，弹孔附近无明显裂纹，如图8所示。

另外，检查发现塞块背部无明显裂纹产生，如图9所示。这与7A04-T6高强钢靶在相同弹体撞击下的断裂情况不同。这说明7075-T651铝合金在双向拉伸应力状态下(环向和径向)的断裂应变高于7A04-T6铝合金。

图10给出了高速摄像相机记录的子弹撞击靶板过程的反弹、嵌入和贯穿的过程。图中椭圆线框中标注的为冲塞。可见，7075-T651铝合金靶板在弹体撞击下发生了剪切冲塞破坏，塞块完整，无明显碎块产生。此外，高速摄像照片显示所有撞击试验中子弹的初始飞行姿态良好，基本上是垂直正撞击。

Fig.8 Shear plugging of the 7075-T651 aluminum alloy plate under blunt projectile impact

图9 试验中冲出的塞块

2.3 有限元计算模型

计算在ABAQUS中进行，建立1/2对称模型，如图11所示。弹体直径和长度分别为5.96 mm和29.82 mm,模型选用变形体，靶的厚度6 mm,直径42 mm(对应环向固定螺栓孔间尺寸)。约束靶板圆周边缘节点的三个平动自由度，弹体和靶板的对称面上设置对称边界条件。设定初始时刻子弹距离靶板的垂直距离为0.1 mm。弹体和靶板的单元类型均为C3D8R，弹体单元轴向尺寸约为1 mm,另外两个方向上的单元尺寸接近但不超过0.3 mm。靶板受子弹撞击部位及附近单元网格边长约为0.1 mm,远离撞击区域时单元尺寸逐渐变大。

在靶心区域建立基于单元的面(同时包括内部和外部面)。采用General contanct方法考虑所有可能接触对间的接触。接触的法向行为采用Hard contact方法，忽略切向的摩擦。由于子弹撞击靶板发生时间极短，其撞击过程假定为绝热过程。

(a) Vi=108.5 m/s

(b) Vi=163.0 m/s

(c) Vi=349.4 m/s

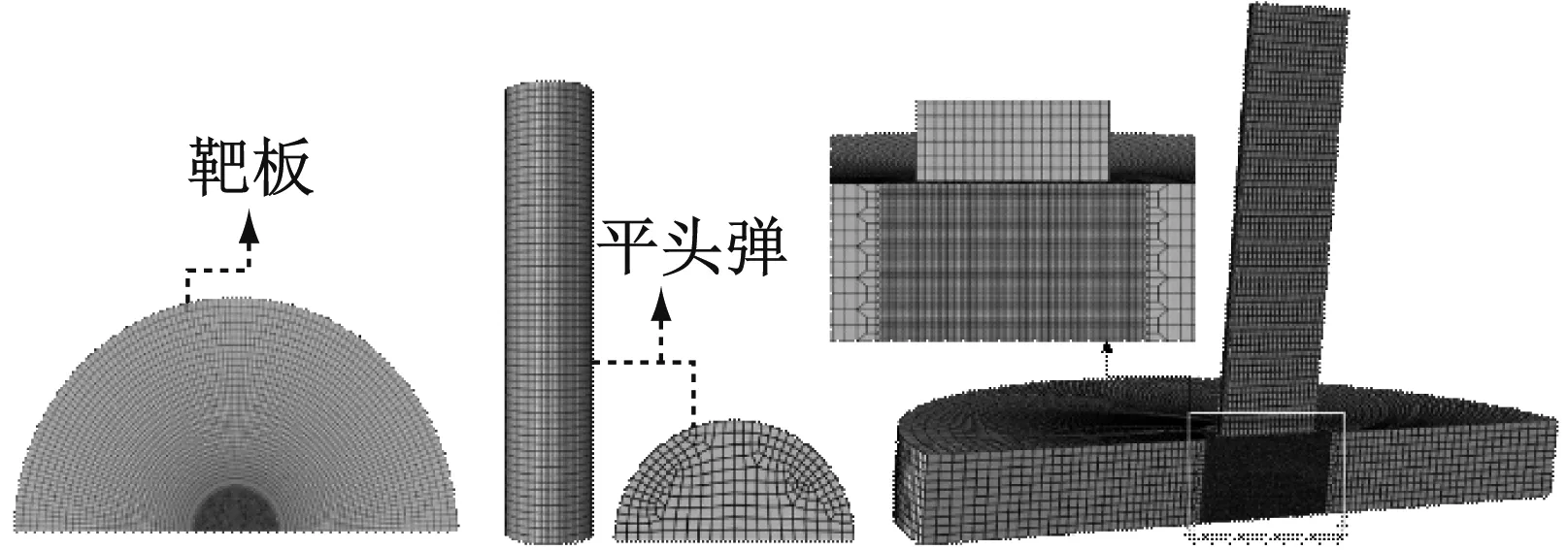
图11 平头弹撞击7075-T651铝合金靶板的有限元模型

Fig.11 FE model of the penetrating of blunt projectiles on 7075-T651 aluminum alloy targets

2.4 有限元计算结果

为揭示Lode角引入断裂准则对弹道行为数值预报结果的影响，本研究共开展了两组平行的数值计算，即本构模型均采用JC，但断裂准则分别采用JC和WM。获得的初始-剩余速度结果如图12所示。

利用R-I公式可获得两组数值计算预报的弹道极限。拟合结果显示JC断裂准则预报的弹道极限为210.2 m/s。而采用WM断裂准则预报的弹道极限为174.6 m/s，与试验结果十分接近。图12中一并显示了R-I预报结果以及试验结果。可见，同时考虑应力三轴度和Lode角的WM断裂准则可以获得与试验一致的弹道极限(比试验值高7%)，而仅考虑应力三轴度影响的JC断裂准则则大大高于了弹道极限(约42%)。

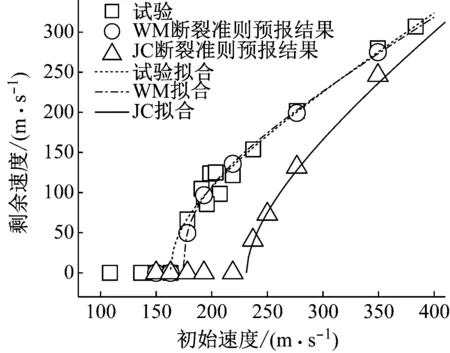
图12 数值模拟得到的初始-剩余速度

图13给出了两组数值模拟计算得到的典型撞击速度下靶板的断裂模式，三个撞击速度分别对应于高速、略高于弹道极限和略低于弹道极限的情形。

从图13中可见:

(1) 当撞击速度较高时，JC和WM断裂准则均预报了剪切冲塞破坏。

(2) 采用JC时冲塞自身破坏严重，采用WM时冲塞表面虽也有开裂，但开裂十分有限。而试验回收的塞块表面没发现明显的裂纹，如图9所示。

(3) 当撞击速度略低于弹道极限时，采用WM断裂准则的数值模拟显示塞块冲出，子弹未穿过靶板，这与试验结果一致。而采用JC断裂准则的模拟则显示子弹反弹，靶板背部开裂，前部冲坑，这与试验结果明显不符。

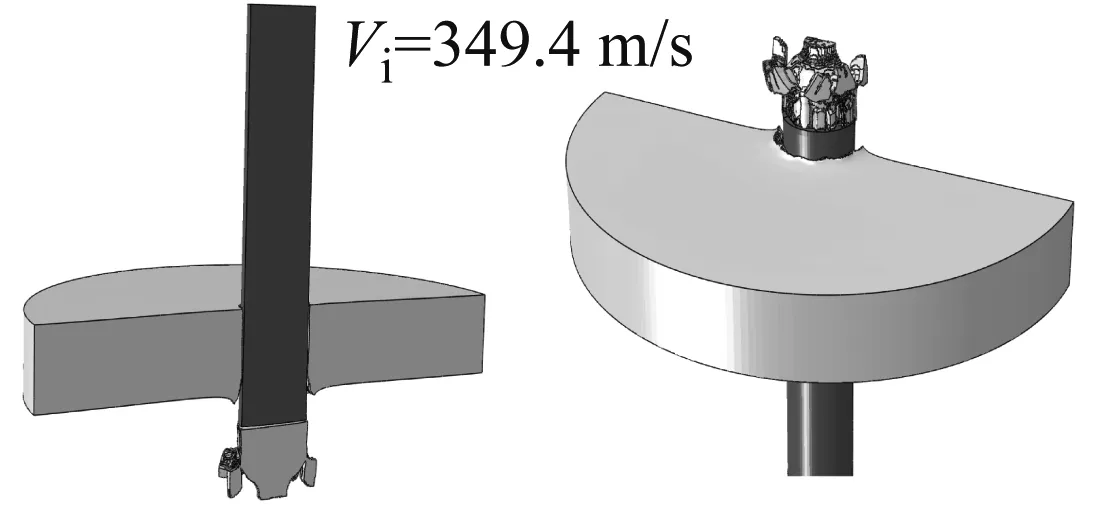
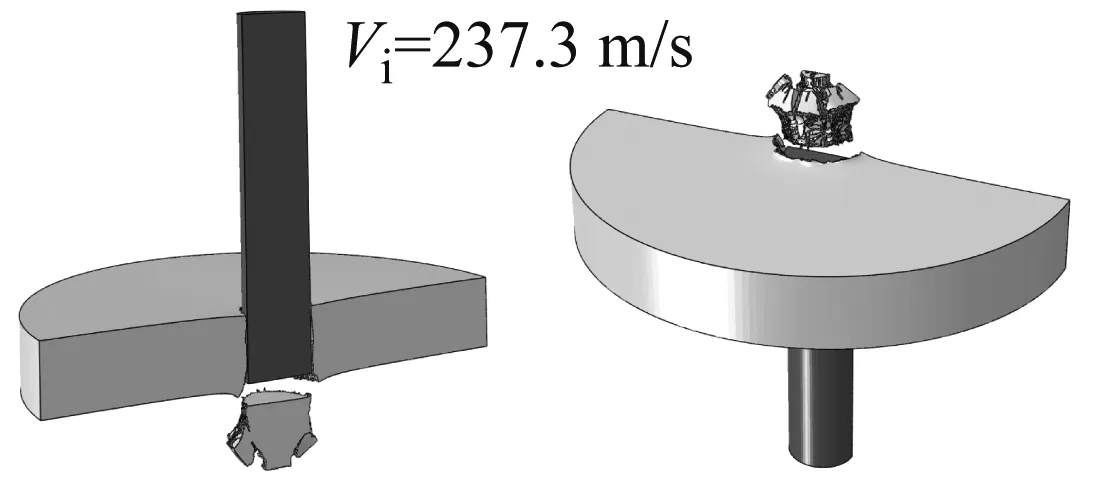
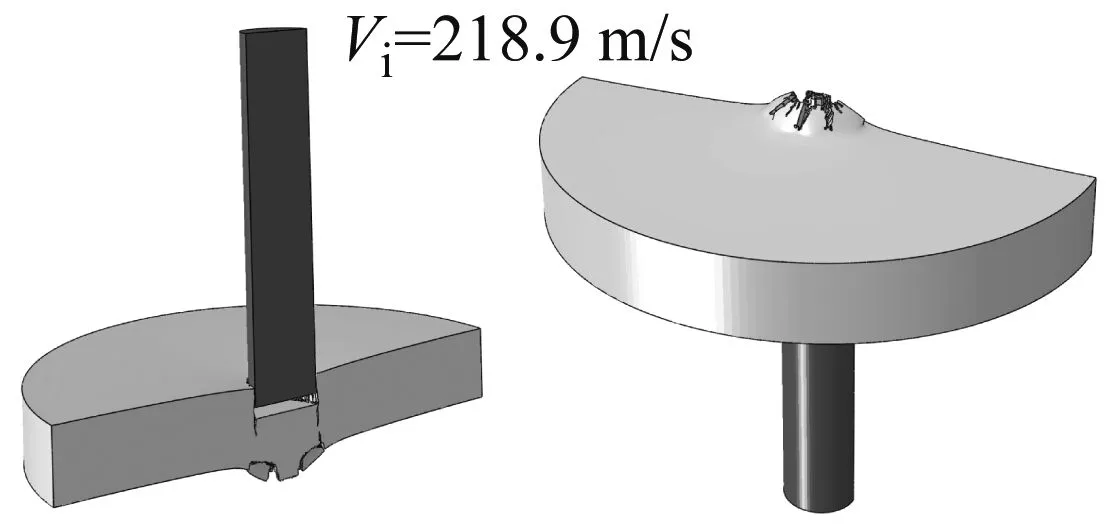
(a) Johnson-Cook

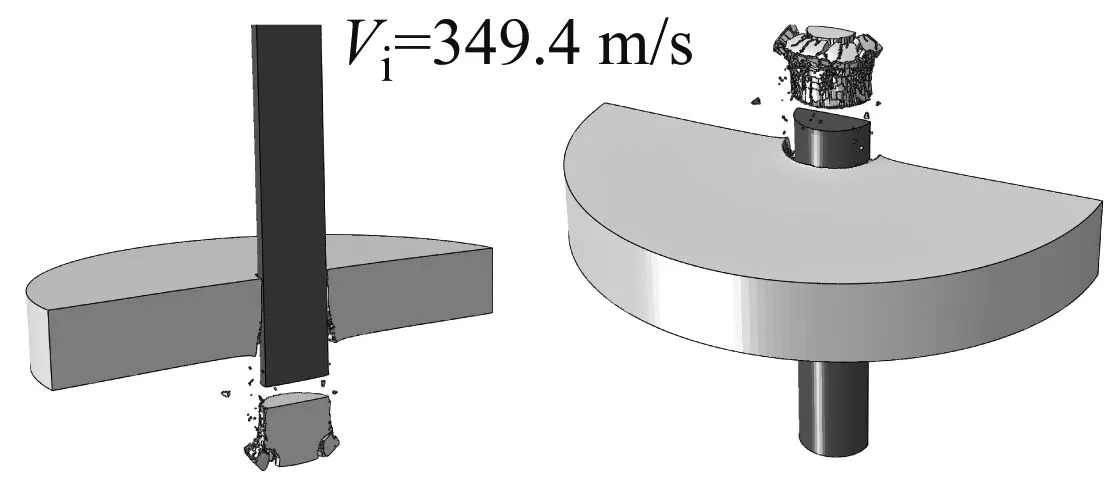
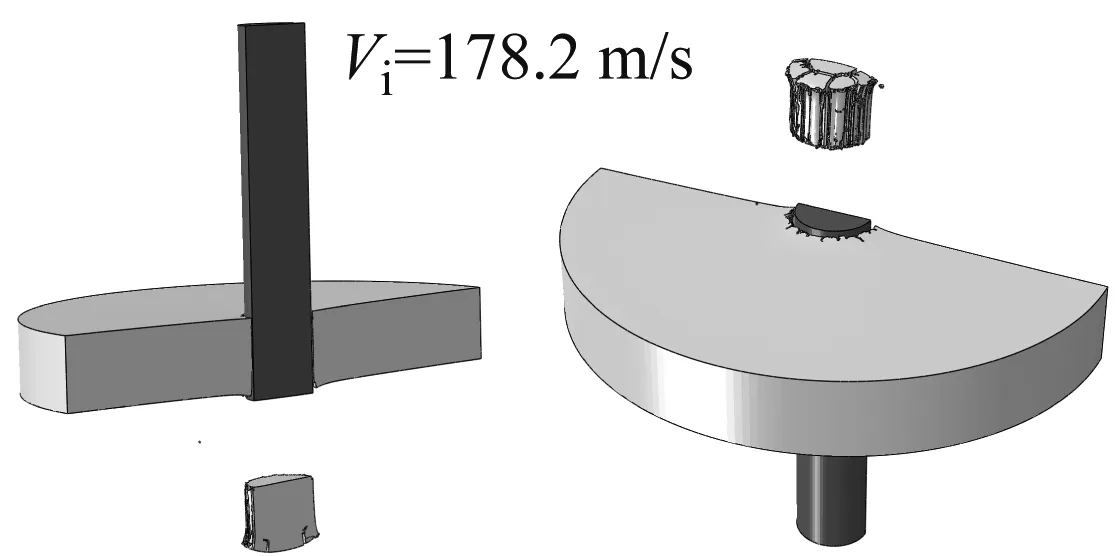
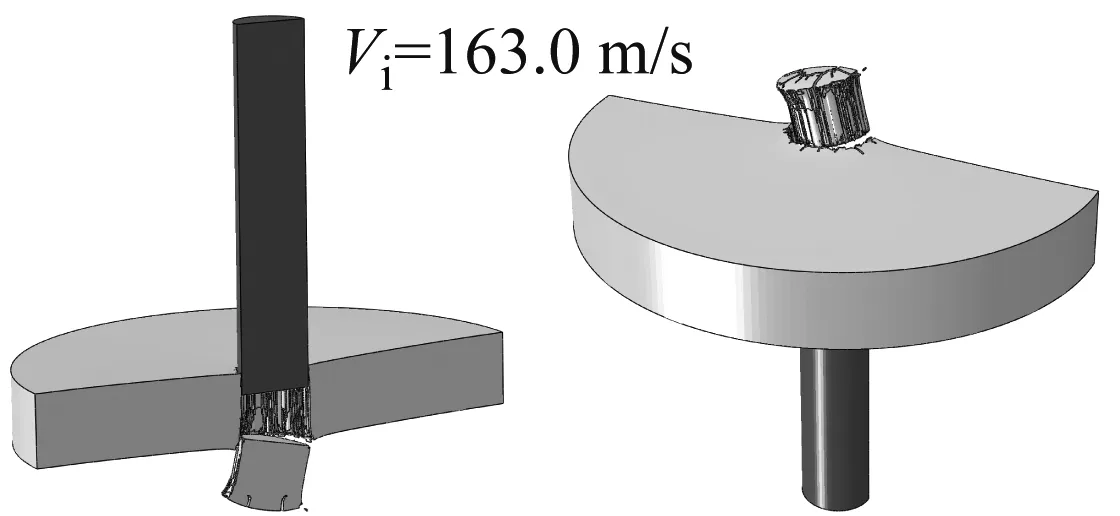
(b) Wen-Mahmoud

3 Lode相关断裂准则影响剪切冲塞数值计算结果的机理

对于受到平头刚性弹体撞击的金属靶板而言，剪切带内材料的力学性能直接影响靶板的抗侵彻能力[27-28]，如剪切带内材料的断裂应变及流动应力随温度和应变率的变化规律等。若剪切带内材料的断裂应变较大，则靶板提供的抗侵彻能力自然就高。根据材料性能测试结果，材料的断裂应变与应力状态密切相关，因此有必要分析剪切带内材料所经受的应力状态。由于裂纹的扩展相比起裂更为容易，因此撞击早期剪切带内的材料是分析的关键。

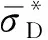
(8)

式中：Df表示撞击结束时单元的损伤值，易知Df≤1。这两个参数在文献[25]中也被用于分析Taylor杆中的主导应力状态。

图14 剪切带内初始失效材料的平均应力状态

Fig.14 Averaged stress states for materials in the shear band at the initial fracture

从图14可见，剪切带内绝大部分初始失效材料的平均应力三轴度介于-1.5和0之间，而平均Lode角介于±0.25之间。这个结果与文献[8,13]的结果一致。

图15在三维空间对比了两个断裂准则预报的材料的断裂应变。可见：在几乎整个应力状态空间JC准则预报的断裂应变均高于WM准则；特别地，在应力三轴度低于0的空间，JC预测的材料延性远远高于WM准则的预报结果。而图14显示剪切带内材料的主导应力状态正是在应力状态低于0的空间，因此采用JC断裂准则时剪切带内的材料的断裂应变极大，极大的断裂应变必然导致损伤增长缓慢，最终导致材料不易失效和较大的抵抗能力。相反，由于WM准则考虑了Lode角的影响，其预报的材料的失效应变较低，因此预报的弹道极限就低。

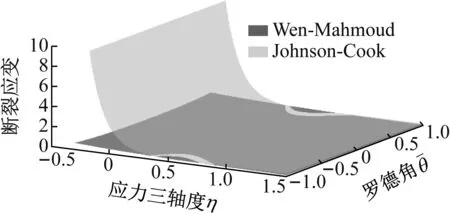
图15 JC和WM断裂准则断裂应变预测结果对比

Fig.15 Comparison of the predicted fracture strain between the JC and WM fracture criteria

4 结 论

为揭示Lode角引入断裂准则对发生剪切冲塞破坏靶板弹道极限和断裂行为数值预报结果的影响，开展了材料性能测试，标定了材料模型；分别采用了Lode无关的JC断裂准则和Lode相关的WM断裂准则，对7075-T651高强度铝靶板在平头刚性弹体撞击下的弹道极限和断裂行为进行了数值模拟和对比分析；并将模拟结果与一级轻气炮上开展的打靶试验结果进行了对比。得到的主要结论为：

(1) 7075-T651铝合金的断裂应变与Lode角相关。考虑Lode角影响的WM断裂准则预报的断裂应变与试验结果一致性较好，而没有考虑Lode角影响的JC断裂准则不能合理预报剪切应力状态下7075-T651铝合金的断裂特性。

(2) 采用Lode相关的WM断裂准则的有限元计算预报的弹道极限和靶板的断裂行为与试验值具有较好的一致性，预报的弹道极限仅高于试验值7%。

(3) 采用Lode无关的JC断裂准则的有限元计算预报的弹道极限高于试验值42%，预报的靶板的断裂行为与试验明显不符。

(4) 剪切带内初始失效材料的应力三轴度低于0，Lode角接近0，即接近平面应变应力状态。

(5) 采用JC断裂准则预报的弹道行为与试验不一致的原因在于过高估计了剪切带内材料的断裂应变。

另外，本文的数值模拟结果也显示，采用Lode相关断裂准则预报时冲塞背部有裂纹出现，这与试验不一致。冲塞部位背部受环向和径向双向的拉应力，即Lode角接近-1，而本文缺少这类试验的材料性能测试数据。这是本文的后继工作。