集中冲击荷载作用下修正Timoshenko梁剪力动载系数研究

曹 振, 马海英, 周军勇, 李 徽, 石雪飞

(同济大学 土木工程学院,上海 200092)

近年来数起车辆撞击桥墩的事故引发了广泛关注，2006年9月8日，一辆挂车撞向位于Corsicana附近跨越IH-45跨线桥的桥墩，造成直径76.2 cm桥墩的破坏[1]；2009年4月17日，湖南郴州市一辆罐车撞上京珠高速一处跨线桥桥墩，2个桥墩被撞断[2]；2012年6月11日，在Dallas附近一辆卡车撞上Dolphin Road跨越I-30公路跨线桥的桥墩，造成桥墩的剪切开裂[3]。这些事故显示在车辆撞击作用下，桥墩产生了剪切破坏。许多文献也报道了设计为在静力荷载作用下发生弯曲失效的钢筋混凝土梁，在落锤冲击试验中会发生剪切破坏[4-6]。这是因为撞击力为冲击荷载，在桥墩内引起的内力分布与静力作用下并不相同，故而造成破坏模式的改变。

因剪切破坏为脆性破坏，降低了结构吸收能量的能力，结构设计中往往禁止发生剪切破坏。但各国长期以来采用等效静力设计法对桥墩进行防撞设计，而等效静力的确定方法是不确定的，比如：美国AASHTO-LRFD(2012)桥梁设计规范[7]第3.6.5条规定，在没有足够防护措施的情况下，桥墩应设计为能够抵抗2 670 kN的等效静力；BS EN 1991-1-7[8]规定按道路的类型确定车辆撞击支撑结构等效静力设计值，并采用风险评估的方法确定撞击力调整系数；中国公路桥涵设计通用规范[9]第4.4.3条规定，汽车撞击力标准值在车辆行驶方向取1 000 kN，在车辆行驶垂直方向取500 kN；El-Tawil等[10]在进行车辆撞击桥墩的数值模拟时认为持续时间较短的峰值动力荷载不必考虑。这些规范和研究没有将撞击力考虑为动力荷载及其在结构构件中引起的动力响应。

为进行构件的抗冲击设计，需要得到构件位移或内力响应时程曲线的最大值。从工程设计角度，就是要使结构能够安全度过这一最大值。Biggs[11]提出了动力荷载系数的概念(Dynamic Load Factor, DLF)，剪力动力荷载系数即为动力作用下梁最大动剪力与冲击峰值荷载作为静力荷载施加在结构上产生的剪力之比。为求得剪力动力荷载系数，需要求出结构在冲击荷载作用下的动剪力响应时程曲线。计算结构动力响应的方法有等效单自由度法(Equivalent Single Degree of Freedom,SDOF)，Bernoulli-Euler梁理论和经典Timoshenko梁理论。Biggs求得了单自由度体系在不同冲击荷载形式下最大动力荷载系数响应谱。等效SDOF系统得到的是构件代表点的响应，求得的内力或支座反力与真实构件存在一定差异[12]。对于冲击荷载，由于Biggs法没有考虑高频高次振型的影响，使得梁中实际作用的动剪力与该方法算出的动剪力有较大的差别，且在集中力冲击荷载作用下用Biggs法求解支座反力时的误差较大。为考虑冲击荷载激发的结构高频响应和其对内力响应的影响，应采用振型叠加法分析结构的动力响应。Magnusson等[13]采用Bernoulli-Euler梁理论定性的分析了简支梁在冲击荷载作用下的早期响应。线弹性梁Bernoulli-Euler受迫振动方程只考虑了弯曲和横向惯性力，高估了高阶模态的自振频率，在高频振动下会引起很大的误差[14]。经典的Timoshenko梁模型考虑了梁的弯曲变形引起的转动惯量和梁的剪切变形，这两个量在模态阶数越高时影响越显著[15]。方秦等[16]采用经典Timoshenko梁理论，计算得到了简支梁在均布和跨中集中冲击荷载下的剪力动力荷载系数。在此基础上，钱七虎等[17]提出了抗爆结构动剪力的实用分析方法，该方法只考虑抗爆结构主要承受的均布荷载作用，不考虑集中荷载情况；只考虑简支梁，不考虑固结梁；所以该方法较粗略。

万春风[18]在经典Timoshenko梁理论的基础上，考虑梁的剪切变形所引起的转动惯量，对经典Timoshenko梁的运动方程进行了修正，修正的Timoshenko梁理论在计算梁自振频率时更加精确[19]。本文基于修正的Timoshenko梁理论，推导出梁在跨中集中力冲击荷载下的内力响应计算方法，计算结果与经典Timoshenko梁理论进行比较，证明修正Timoshenko梁理论的优越性，在此基础上得到跨中集中力冲击荷载作用下简支梁和固结梁剪力动力荷载系数，为设计提供方便精确的确定剪力需求的方法。

1 修正Timoshenko求内力响应

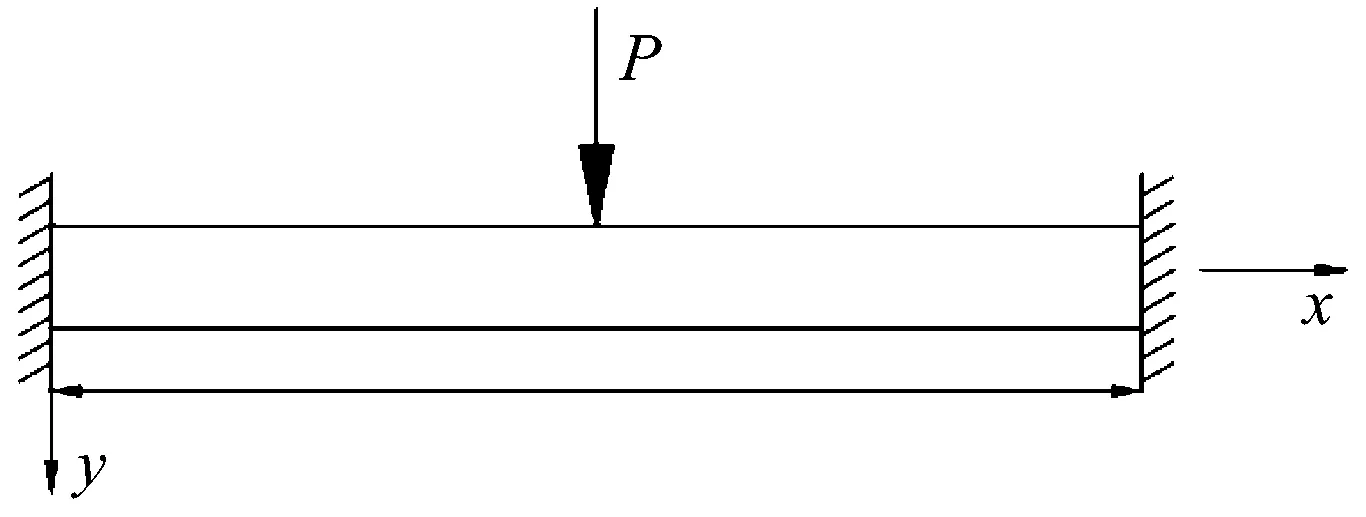
图1 梁跨中受集中力冲击荷载作用示意图

Fig.1 Diagram of the concentrated impact load on the midspan of beam

经典Timoshenko梁理论同时考虑了由弯曲引起的转动惯量和剪切变形，在此基础上考虑由剪切变形引起的转动惯量的影响，得到修正Timoshenko梁的运动方程：

(1)

(2)

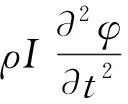
1.1 修正理论的正交条件

修正Timoshenko梁在自由振动情况下运动方程为

(3)

设第n阶振型的位移函数为

yn(x,t)=Yn(x)tn(t)

(4)

将式(4)代入式(3)，得

(5)

同理可得

(6)

式(5)左右两边乘以Ym(x)，式(6)左右两边乘以Yn(x)，并相减得

(7)

对式(7)在梁长度内进行积分，通过简支梁或固结梁在跨中受到冲击荷载作用时的边界条件可得：

(8)

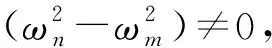
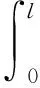
(9)

1.2 冲击响应计算

令Timoshenko梁在荷载强迫作用下的位移为：

(10)

式中：Tn(t)为表示第n阶振型在总位移中所占比例的关于时间的幅值函数。

代入式(1)和式(2)得

(11)

由式(5)可知：

(12)

将式(12)代入式(11)得

(13)

式(13)两端乘以Ym(x)并积分，利用正交条件可得

(14)

令Mn、Pn为相应于Timoshenko梁第n阶振型的广义质量和广义荷载，则

(15)

在均布荷载的情况下

(16)

若荷载为集中荷载P=P0f(t)，其中P0为冲击荷载的峰值，f(t)为冲击荷载随时间变化的函数。则应用Dirac函数积分得

(17)

方程(14)变为

(18)

用Duhamel积分解该微分方程，

(19)

为了求等效质量Mn，需要求振型位移形状函数Yn(x)，第n阶振型的位移形状函数为

(20)

式中g1，g2，g3和g4都是频率ω的函数：

(21)

根据边界条件求出梁的自振频率ωn和振型形状函数Yn(x)，将求得的梁的自振振型形状函数Yn(x)和关于时间的幅值函数Tn(t)代入式(22)计算出梁内剪力响应。

(22)

1.3 荷载形式

本文选取的冲击荷载为无增长时间的直角三角形荷载和有增长时间的三角形荷载，如图2所示。在进行防护结构的设计时，爆炸荷载是按照无增长时间的压力时程曲线考虑的，即当冲击波到达时刻，超压几乎是瞬时达到峰值，无增长时间的直角三角形荷载是一种简化。在某些情况下集中力冲击荷载也可以按照直角三角形荷载来考虑，比如曾翔[22]在进行钢筋混凝土梁的落锤冲击试验时得到了冲击力的时程为持续时间1.5 ms的脉冲荷载，荷载几乎是瞬时达到最大峰值力，可以认为是无增长时间的三角形荷载，如图2(a)所示。

Thilakarathna等[23]在进行车辆撞击桥墩的研究中建议使用等腰三角形荷载，荷载持续时间为100 ms。El-Tawil等[24]进行车辆撞击桥墩的数值模拟，得到了持续时间约为10 ms的脉冲荷载，荷载形状也为等腰三角形。Buth等[25]进行了车辆撞击桥墩的试验，得到撞击力时程为等腰三角形脉冲荷载。但是由于车辆构造的不同，车辆的前端刚度也会不同；或当车辆刚性部件如发动机撞击桥墩时，其荷载可能增长很快，增长时间占总持续时间的比值可能较低[26]。所以有增长时间的三角形荷载，通过ζ值的改变调整增长时间占荷载持时的比值，ζ=0.5时即为等腰三角形荷载，如图2(b)所示。

(a) 无增长时间三角形荷载(b) 有增长时间三角形荷载

图2 无增长时间的三角形荷载和有增长时间的三角形荷载

Fig.2 Diagram of triangular impact load with and without increasing time

对于无增长时间的三角形荷载，其荷载变化函数为：

(23)

式中:td为荷载持续时间。

一般三角形荷载变化函数为

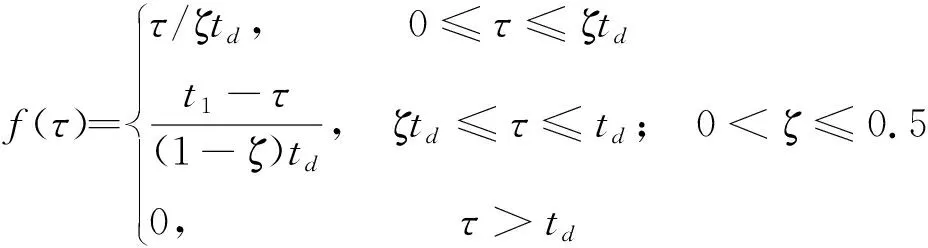
(24)

式中:ζ为荷载增长时间与荷载持续时间的比。

1.4 Timoshenko梁经典与修正理论计算结果比较

如图3所示，对两端固结梁的支座截面和距离跨中一半梁高截面的剪力动力荷载系数时程曲线进行研究，选取长细比为16.7的A梁和长细比为6.2的B梁，A梁为直径0.6 m的圆形截面，B梁为高1.4 m，宽0.5 m的矩形截面。取材料密度为ρ=2 600 kg/m3，弹性模量为E=30 GPa。在跨中受到无增长时间三角形集中力冲击作用，荷载持续时间td分别为15 ms和10 ms。

剪力响应实际上由无穷阶振型响应组成，一般计算都是截取前几阶影响较大的阶次。首先对计算结果的收敛性予以证明。图4(a),(b)是A梁和B梁在冲击荷载作用下，取不同阶数振型计算得到的支座截面剪力时程曲线。由图可以看出，取前3阶和前5阶振型得到的结果与最终结果仍有差异，取前20阶和前50阶振型得到的曲线已经重合，说明计算结果收敛。另外，取前20阶振型得到的最大剪力比只取前5阶和前3阶振型时要大，说明高阶振型对剪力的影响比较显著。

图3 剪力时程选取位置示意图

图4(c)～(f)为根据经典Timoshenko梁理论、修正Timoshenko梁理论和ABAQUS实体单元建模计算的结果。由图可以看出，在梁长细比较大的情况下，经典Timoshenko梁和修正Timoshenko梁计算结果与ABAQUS计算的结果都比较相符。但是梁长细比的较小的时候，经典Timoshenko梁理论计算结果与ABAQUS产生了偏差。如图4(e)所示，经典理论计算结果表明，在剪切波传递到支座之前，支座截面就已经有剪力产生，这与实际情况是不相符的，而且根据剪力DLF时程曲线中得到的最大剪力是偏大的。如图4(f)所示，经典理论计算得到的距跨中一半梁高位置处的剪力也明显与ABAQUS计算结果偏差较大。而在梁长细比较小的情况下，根据修正Timoshenko梁理论计算的到的结果与ABAQUS计算结果都符合较好。

2 剪力动力荷载系数

由图4可以看出，跨中附近剪力DLF要小于支座部位的剪力动力荷载系数，即剪力响应最大值会发生在支座截面，所以本文基于修正Timoshenko梁理论进行简支梁和固结梁在跨中集中力冲击荷载作用下的支座截面最大剪力DLF计算。

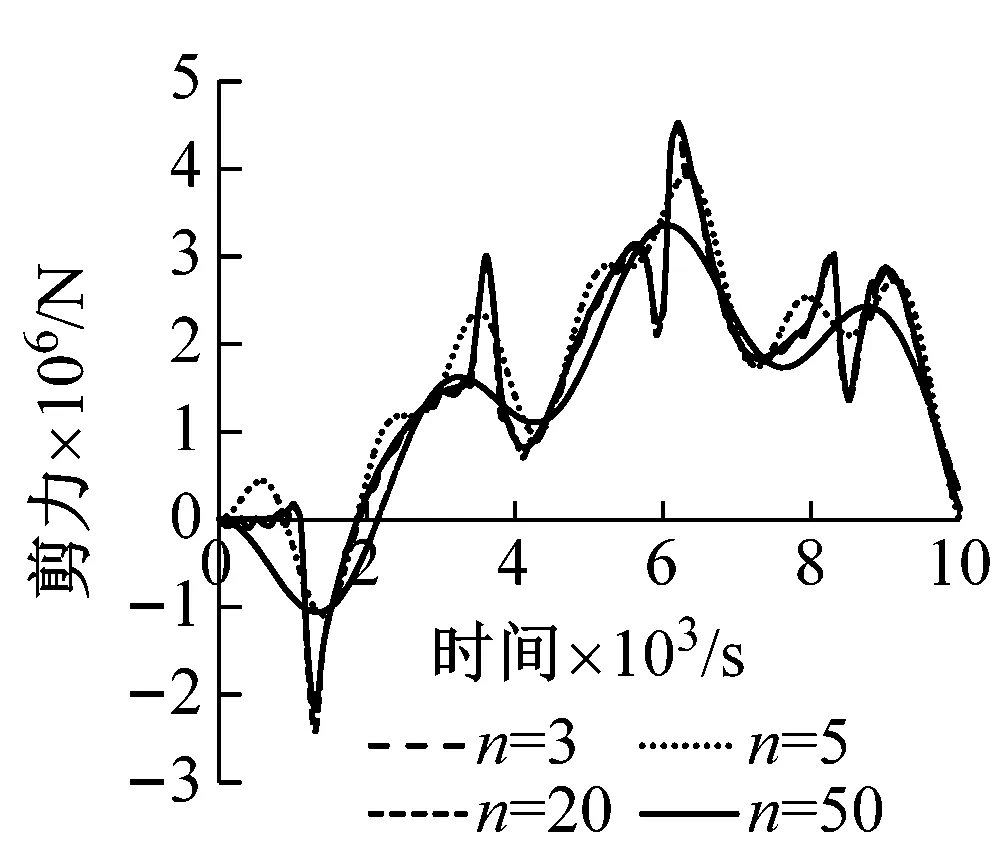
(a) 取前n阶振型算得A梁支座截面剪力时程

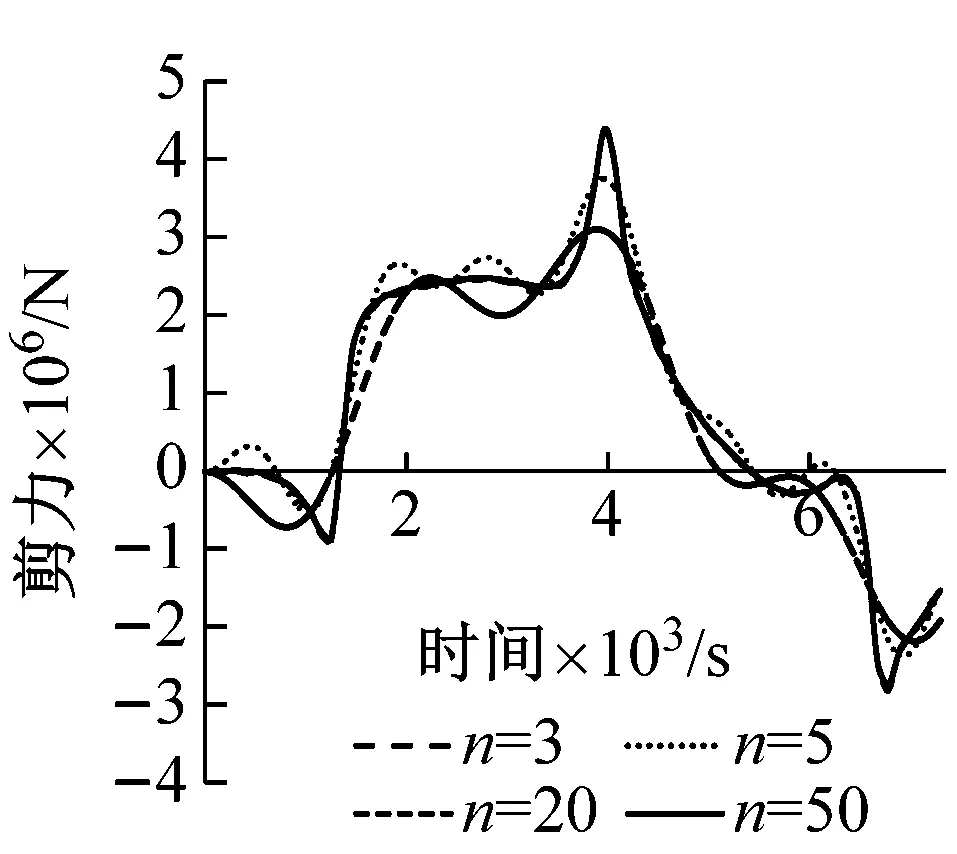
(b) 取前n阶振型算得B梁支座截面剪力时程

(c) A梁支座截面剪力DLF时程曲线

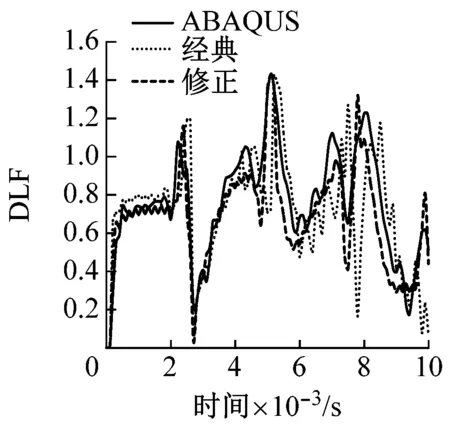
(d) A梁距跨中一半梁高截面剪力DLF时程曲线

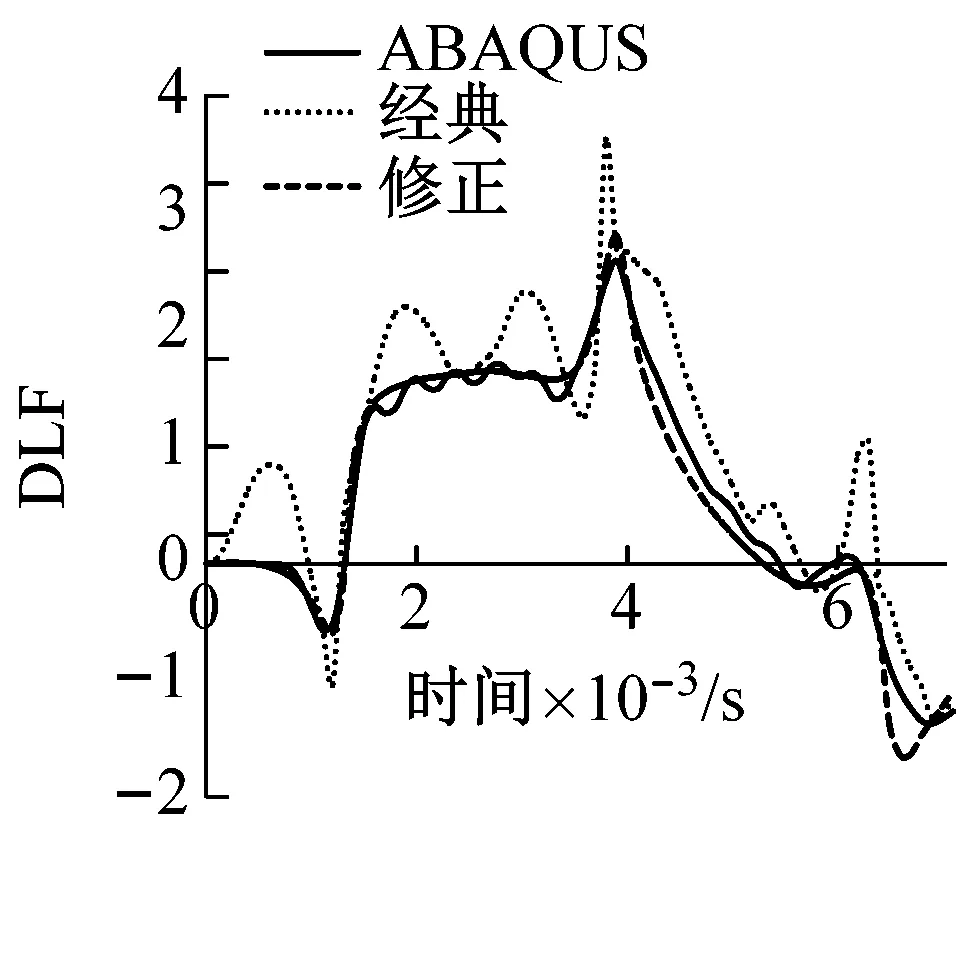
(e) B梁支座截面剪力DLF时程曲线

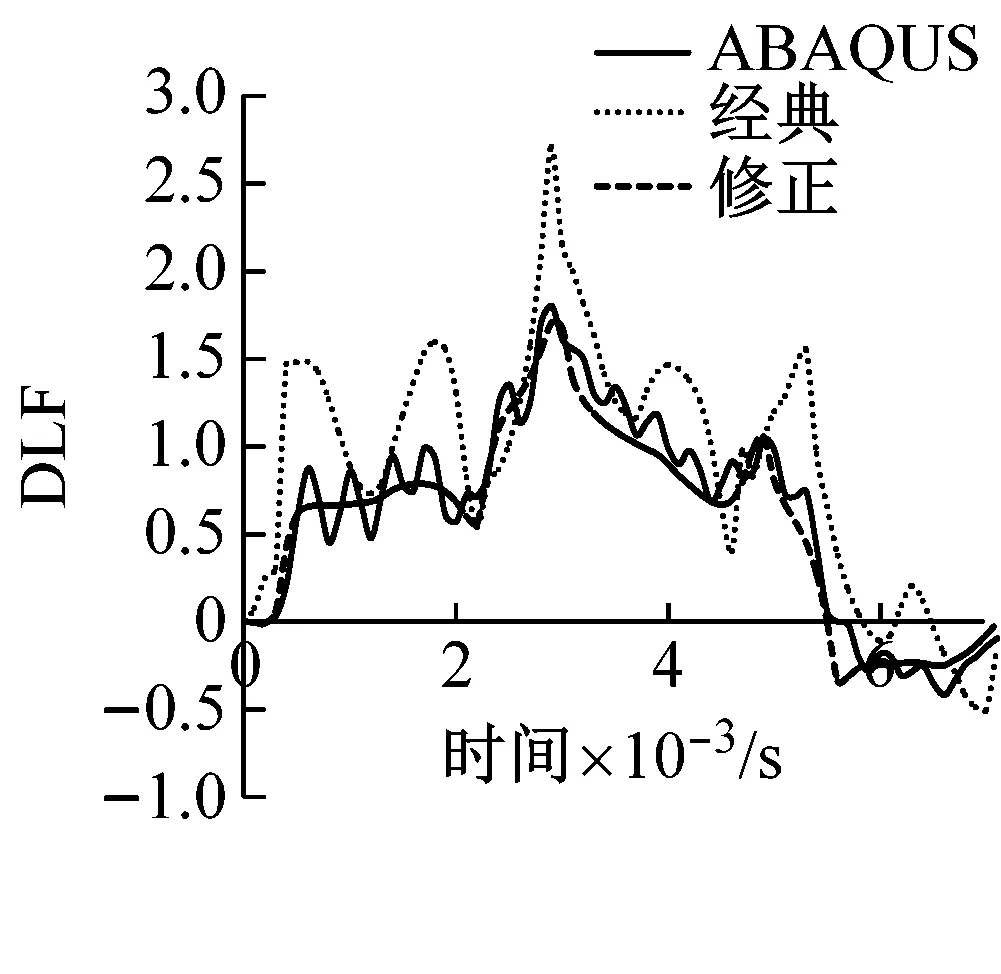
(f) B梁距跨中一半梁高截面剪力DLF时程曲线

图4 梁在跨中冲击荷载作用下剪力DLF时程曲线

Fig.4 DLF Time-history Curve of Shear Force under the Impact of concentrated Impact at midspan

2.1 无增长时间的三角形荷载

图5为不同长细比固结梁和简支梁在不同持续时间无增长时间突加三角形冲击荷载下支座截面剪力动力荷载系数，td/T1为横坐标，以对数坐标显示，T1为梁第一阶自振周期。由图可以看出，在无增长时间的三角形荷载作用下：①支座截面最大剪力DLF随着td/T1的增加而增加；②支座截面最大剪力DLF和长细比并没有单调关系，即同样的td/T1，支座截面剪力DLF随着长细比的增加或减小并不会单调变化；③冲击位置在跨中时，支座剪力DLF随着td/T1的增加会趋近与某一个值；④在td/T1很大时，固结梁和简支梁的支座截面最大剪力DLF都达到了2.5以上，与按照等效单自由度计算得到的最大DLF为2相比，提高了很多；⑤同时可以看出简支梁支座截面处最大剪力DLF比固结梁的要小。

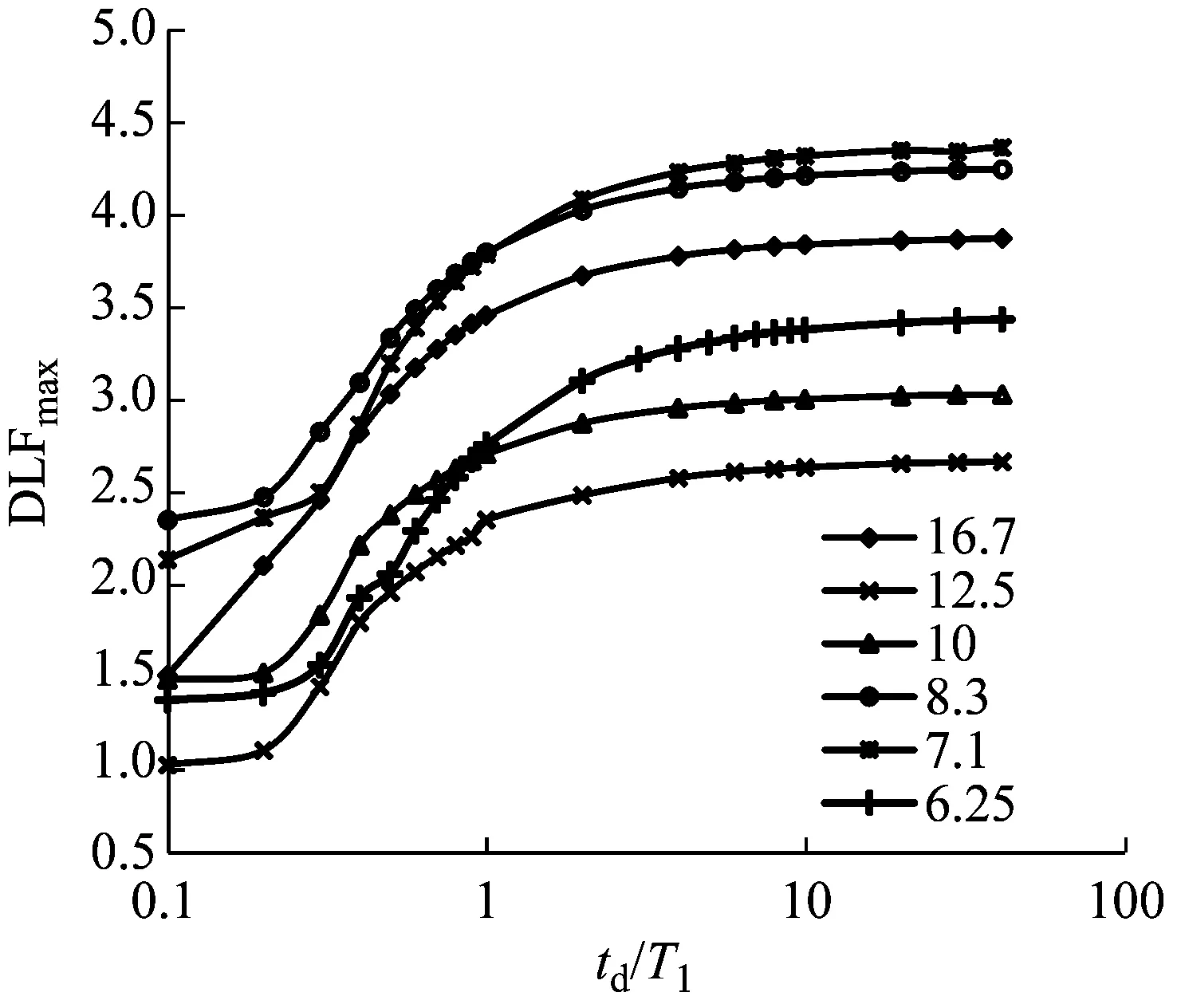
(a) 固结梁

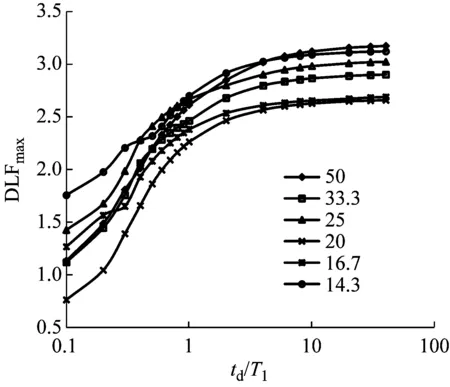
(b) 简支梁

2.2 有增长时间的三角形荷载

对于有增长时间的三角形荷载，增长时间所占持续时间td的比值为ζ。不同ζ值的三角形荷载作用于长细比为10的固结梁和长细比为20的简支梁跨中时，梁端剪力响应最大动力荷载系数,如图6所示。

由图6可以看出：①在增长时间较小的情况下，即ζ<0.1时，支座剪力最大DLF随着td/T1变化的趋势与无增长时间三角形冲击荷载作用下的相同；②在增长时间较大的情况下，即ζ>0.1时，随着td/T1的增长，最大剪力DLF会首先上升，在td/T1=0.8附近达到最大值，之后出现下降的趋势；③0.1≤ζ<0.3时，固结梁在不同的td/T1下能够达到的支座最大剪力DLF比简支梁能够达到的最大剪力DLF要大，ζ≥0.3时，两者之间区别不是很明显；④简支梁在td/T1<0.5时，不同ζ值的最大剪力DLF是相近的，且DLF随着td/T1减小会下降，而固结梁在td/T1<0.3时，最大剪力DLF会稳定在1.4附近。由图6可以看出，在同样荷载持续时间的情况下，延长荷载的增长时间比例，即提高ζ值，可以显著降低支座反力的DLF；即在有同样峰值和同样冲量的冲击荷载作用下，增加荷载的增长时间，可以降低最大剪力响应；所以在防撞设计中，通过设置缓冲防撞设施不仅可以增加荷载持续时间，减小荷载峰值，还可以提高荷载增长时间比例，降低最大动剪力响应。

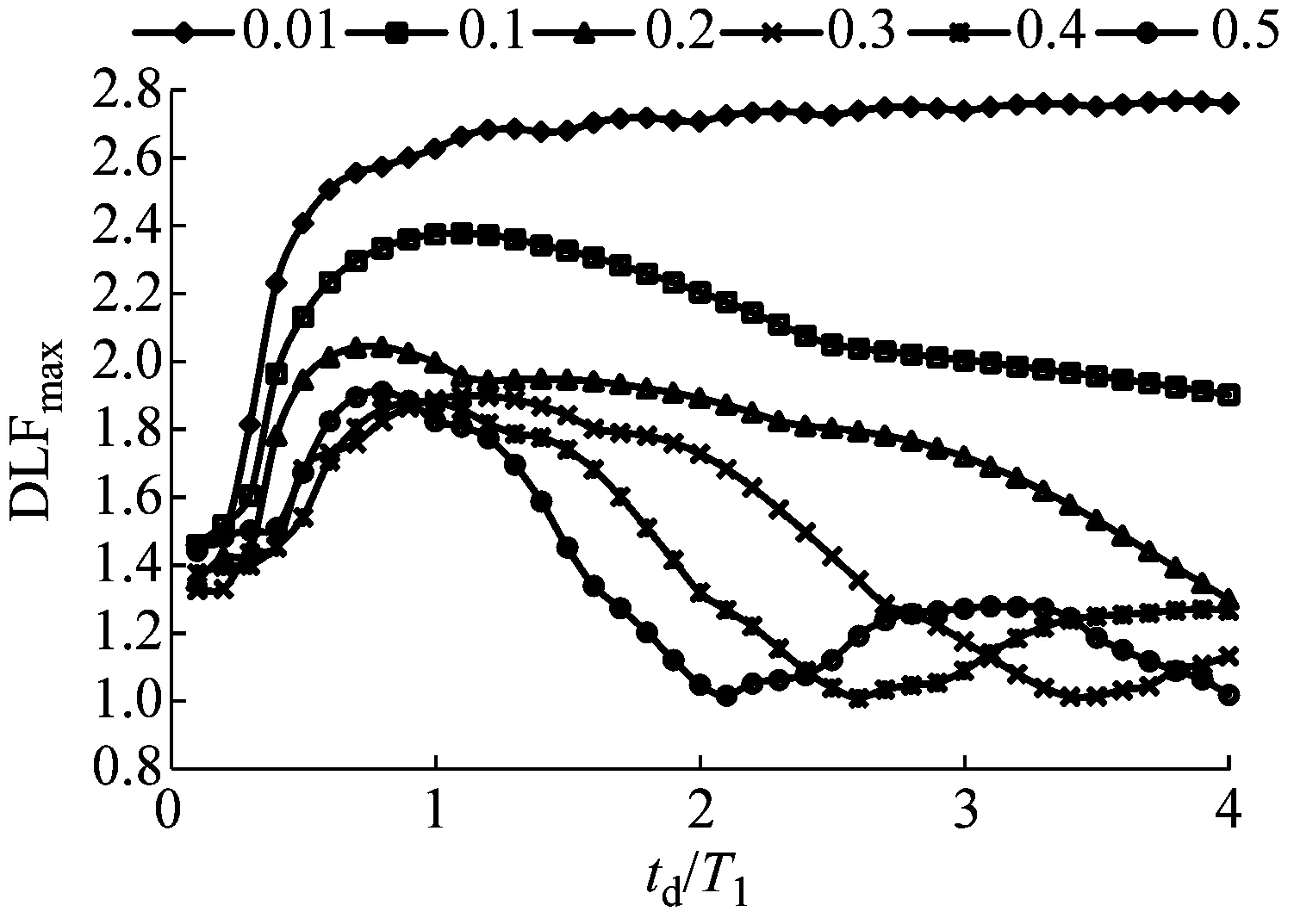
(a) 固结梁

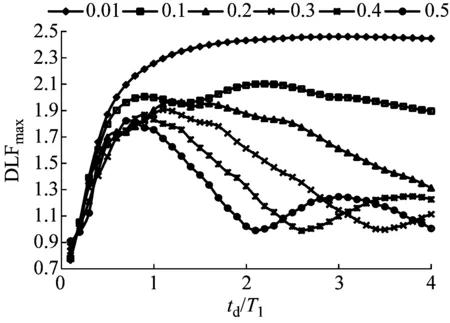
(b) 简支梁

许多文献中得到了等腰三角形的车辆撞击冲击荷载，所以取ζ=0.5，研究不同长细比的梁在等腰三角形冲击荷载作用下的最大剪力DLF。图7为不同长细比的固结梁和简支梁在跨中受到等腰三角形荷载时的最大剪力动力荷载系数。由图7可以看出，梁在跨中受到等腰三角形冲击荷载作用时，随着td/T1增长，最大剪力DLF会先增长，在td/T1增长到0.8附近是达到最大值；之后开始降低，随着td/T1的增长，最大剪力DLF仍有起伏，但都小于最大值。固结梁和简支梁最大剪力DLF值都约为1.9，相对于单自由度体系得到的最大值为1.5，提高到了约27%；在td/T1<0.5时，固结梁跨中受等腰三角形冲击荷载作用时，随着梁长细比的减小最大剪力DLF逐渐增大；在td/T1>0.5时不同长细比的梁最大剪力DLF是相等的；对于简支梁，不同长细比的梁在不同td/T1下，最大剪力DLF都是相等的。

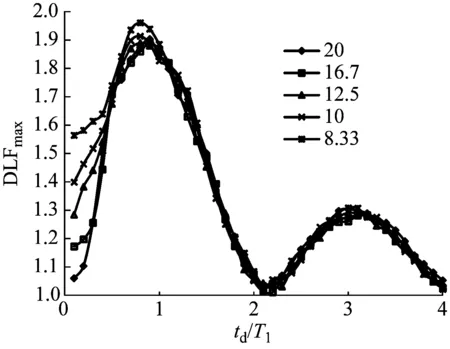
(a) 固结梁

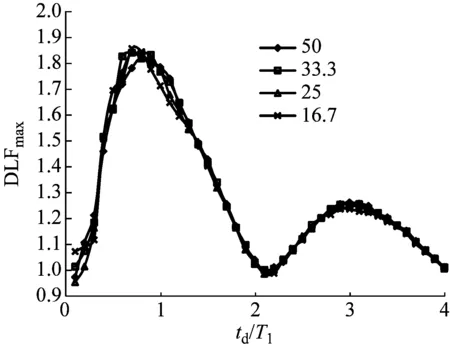
(b) 简支梁

2.3 最大剪力DLF计算方法

通过以上方法获得大量数据进行回归拟合，得到最大剪力DLF的计算公式。固结梁和简支梁在跨中受到无增长时间三角形冲击荷载作用下，剪力DLF随td/T1变化曲线符合增长模型，所以采用增长模型函数进行拟合。在等腰三角形荷载作用下剪力DLF随td/T1变化采用多项式进行拟合。

固结梁在跨中受到无增长时间三角形冲击荷载作用下，最大剪力DLF计算公式为式(25)，该公式的相关指数R2=0.985。

(25)

其中

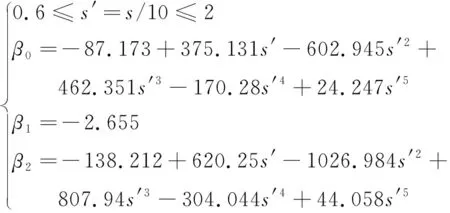
(26)

简支梁在跨中受到无增长时间三角形冲击荷载作用下的最大剪力DLF计算公式仍采用式(25)，其他参数按式(27)计算，得到的相关指数R2=0.974。

(27)

固结梁在跨中受到等腰三角形冲击荷载时，得到的最大剪力DLF计算公式为：

(28)

式中:t1=td/T1≤4，该公式的复判定系数R2=0.924。

简支梁在跨中受到等腰三角形冲击荷载作用时，得到最大剪力DLF计算公式为：

(29)

式中:t1=td/T1≤4，该公式的复判定系数为R2=0.89。

在确定受冲击荷载作用构件的剪力需求时，可根据剪力动力荷载系数确定剪力需求。首先将荷载峰值作为静力荷载求出跨端最大静剪力；然后确定结构构件的长细比和第一阶自振周期，再根据冲击荷载形式和持续时间，求得相应的剪力动力系数；最大动剪力即为最大静剪力乘以剪力动力系数。得到的拟合公式可以方便的确定墩柱在车辆撞击力作用下的剪力需求，相比较现有规范对车辆撞击等效静力设计值的规定，动力分析过程清晰，剪力动力放大系数的确定有依据且精度较高。

3 结 论

(1) 本文根据修正Timoshenko梁运动方程得到了其正交条件，并在此基础上得到了梁在冲击荷载作用下的内力响应计算方法，根据该方法得到不同长细比的梁在跨中受到冲击荷载时的最大剪力动力荷载系数。计算结果表明，在梁长细比较小时，修正Timoshenko梁理论计算的结果较为精确。

(2) 得到梁的最大剪力动力荷载系数表明：在无增长时间三角形冲击荷载作用下，动载系数随着荷载持续时间的增长而增长，并趋近于某一渐进值，该值受长细比影响较大；在有增长时间的三角形冲击荷载作用下，剪力动载系数会随着增长时间占荷载持续时间的比例增加而减小；在等腰三角形冲击荷载作用下，荷载持续时间约为梁第一阶自振周期的0.8倍时，剪力动载系数达到最大，且长细比对动载系数影响较小。

(3) 对数据进行拟合分析，得到固结梁和简支梁在跨中受到无增长时间的三角形荷载和等效三角形荷载作用下，支座最大剪力动载系数的计算公式，可以方便的用来确定受冲击构件的剪力需求。