基于小波包变换-主元分析-神经网络算法的多电平逆变器故障诊断
,,
(山东科技大学 电气与自动化工程学院,山东 青岛 266590)
目前,电力电子技术在交直流输电、新能源电力变换、变频电机控制和配电网谐波治理等方面得到了广泛应用。电力电子设备突发故障会导致设备损坏、生产停滞甚至人员伤亡等,因此故障诊断是保障电力电子设备安全稳定运行的基础[1-2]。逆变器是一种应用广泛的电力电子设备,其中级联H桥多电平逆变器由于开关损耗低、稳定性高、输出电压谐波分量少等优点得到了快速发展。但是,随着功率器件数量的增多,发生故障的概率也随之增大。据统计分析,逆变器故障主要分为功率器件的短路故障和开路故障。通常,当功率器件出现短路故障时,急剧增加的电流会导致保护熔断器断路,从而短路故障最终会转化为开路故障。因此,在逆变器故障诊断的研究中,以功率器件的开路故障诊断为主[3-4]。
近年来,随着智能算法的不断发展,智能故障诊断方法被广泛地应用在故障诊断方面。文献[5]针对电力电子变流器提出基于故障与基本测量相关性的逻辑诊断方法,其主要目的是使电力电子系统能够在故障出现时容错运行,以适应智能电网的要求并延长其工作寿命。文献[6]针对三相逆变器提出一种基于三相电流极值及其比值,并结合概率神经网络的开路故障诊断策略。通过以各相输出电流的极值和比值作为诊断过程中的特征向量,利用概率神经网络对故障进行分类定位。文献[7]针对三相逆变器提出一种结合小波与Concordia变换的方法,提取三相输出电流的故障特征值作为故障诊断的特征向量,并利用传统的支持向量机方法对故障进行分类。文献[8]针对逆变器中功率管的开路故障,提出一种非侵入式的逆变器开路故障在线诊断与定位方法。利用故障线电压包络线与实测线电压进行比较对故障进行定位。文献[9]针对三相逆变器提出一种基于贝叶斯网络的三相逆变器数据驱动故障诊断方法,首先测量不同故障模式下两路输出线电压,采用FFT(fast Fourier transform)变换提取信号特征,然后采用主成分分析法降低维数,再利用贝叶斯网络对故障进行检测和分析。文献[10-11]通过小波包变换对三相逆变器故障进行分解,然后分别通过相空间重构和小波包包络流行学习算法进行学习并重构得到故障特征,再对故障进行分类定位。
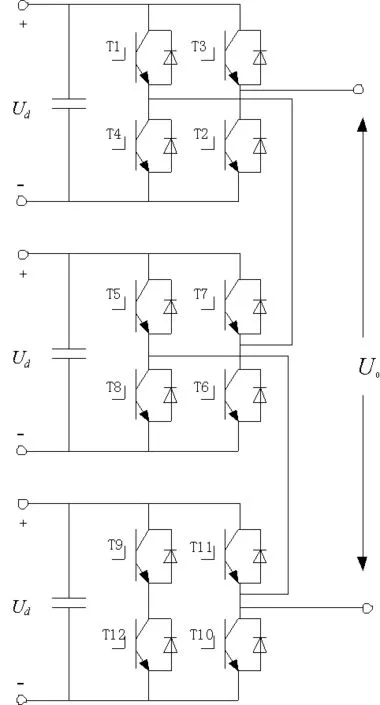
图1 级联H桥七电平逆变器Fig.1 Cascade H-bridge seven-level inverter
目前,关于逆变器的故障诊断多集中于三电平逆变器电路,多电平逆变器的故障诊断还需要进一步深入研究。为此,针对级联多电平逆变器提出一种基于小波包变换-主元分析-神经网络算法的故障诊断方法。首先,通过仿真实验获取原始故障数据,然后通过小波包变换(wavelet packet transform,WPT)对原始信号进行多尺度小波包分解并重构提取小波包能量作为故障特征向量,再利用主元分析(principal component analysis,PCA)方法降低故障特征维度,最后将得到的低维特征向量作为BP神经网络的输入,经网络训练之后进行故障分类,达到多电平逆变器故障诊断的目的。
1 多电平逆变器故障模型
逆变器故障一般分为开路故障和短路故障两种情况,本研究针对逆变器的功率管的开路故障进行分析。在负载变化的情况下,交流侧输出电流波动较大,不利于分析研究,而此时电压信号则受其影响很小,因此选取逆变器的交流输出电压作为故障信号。
级联H桥逆变器每相由多个H桥单元级联而成,逆变器输出相电压的电平数L与单元级联个数N存在关系式L=2N+1[12]。为方便分析故障的特点,选取由3个级联单元组成的七电平级联H桥逆变器作为研究对象。七电平逆变器由12个功率管组成,单个功率管开路的情况是12种,连同正常状态一共有13种状态。图1为单相3单元级联H桥七电平逆变器拓扑图。图2给出了功率管12种故障情况下交流输出电压信号。
2 故障特征提取
在电力电子电路故障诊断过程中,有些系统可以通过建立数学模型的方式对测量变量进行估计,输出电压残差来进行故障分析。但是,当所检测系统数学模型的建立比较困难或者是建模过程相对复杂时,可以先采用智能算法对采集的原始数据进行故障特征提取,然后再对故障进行智能分类,这样可以极大地减少工作量,提高工作效率。将原始数据先通过WPT进行特征提取,然后再利用PCA对高维特征向量进行主元分析达到降维的目的,从而减轻分类网络训练压力,提高分类准确率。
2.1 基于WPT的特征提取
小波变换因其在时频分析中所表现出的优越特性被广泛应用在信号处理上,但是小波变换在每层分解中仅对低频分量进行分解,所以存在高频段频率分辨率差的缺点。相比小波变换,小波包变换具有更高的时频分辨率,是一种更为精细的分析方法[13]。
小波变换将信号分解分为逼近和细节两个过程。信号f(t)的小波变换[14]可以表示为:
(1)
式中:φ(t)为小波基,a为尺度参数,b为位移参数。但在某些应用中,小波变换不能生成足够精细的频谱分辨率,而小波包变换的使用有助于克服这一缺陷。给定小波函数和尺度函数,可以通过公式(2)进行小波包分解。
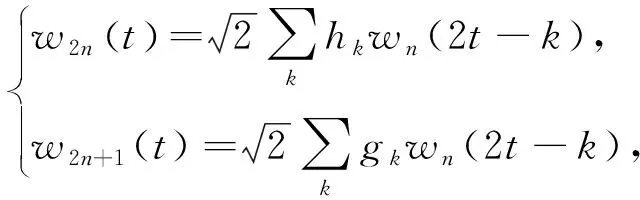
(2)
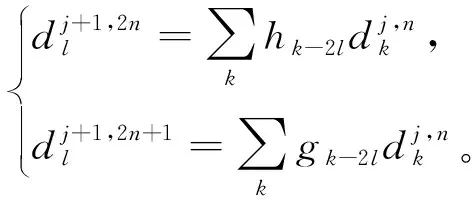
(3)
(4)
小波包分解如图3所示(以3尺度小波包分解为例)。

图3 小波包分解示意图Fig.3 Diagram of wavelet packet decomposition
利用小波包变换提取故障特征的步骤如下:
1) 收集原始故障数据,为了尽量准确地反映故障特点,要确保原始数据达到一定的数量;
2) 对原始数据进行多尺度小波包分解,提取分解得到的最后一层的各个频段的信号特征;
3) 重构小波包分解系数,求出各频带的信号能量,提取与故障有关的几个频带进行重构;以3层分解为例,各频段信号能量的计算公式为:
(5)
其中,xjk表示重构信号W3j的离散点的幅值。
4) 构造特征向量,利用所求能量值构造故障特征矩阵。即
I=[E30,E31,E32,…,E37]=[I0,I1,I2,…,I7]。
(6)
2.2 基于PCA的特征降维
PCA是一种数学降维方法,该方法本质是将原来数据经过一定处理,重新组合成新的相互无关的变量。PCA降维的步骤如下[9, 15]:
1) 对原始数据进行标准化处理。
若X为原始数据矩阵,xij为矩阵X的元素,则标准化处理公式如下:
(7)
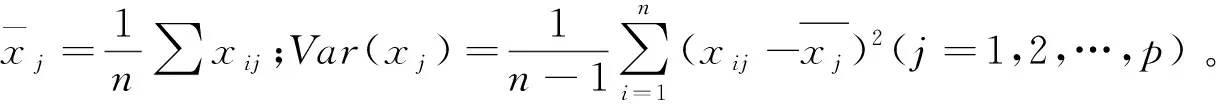
2) 计算样本数据的相关系数矩阵。
假设标准化后的矩阵仍用X表示,则相关系数矩阵为:
(8)
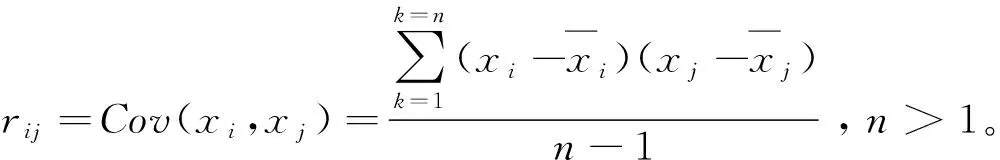
3) 计算相关系数矩阵的特征值和特征向量。
4) 根据特征值的占比,计算各主成分的贡献率。根据贡献率的大小选取主成分,原则上累计贡献率不得小于85%。

图4 三层神经网络结构图Fig.4 Structure of three-layer neural network
3 故障分类
故障分类采用BP神经网络。BP神经网络作为一种多层前馈神经网络,由输入层、隐含层和输出层共同组成。
图4中Xi表示输入层第i个节点的输入,yk表示输出层的第k个节点的输出。Wij和Wjk为BP神经网络的权值。BP神经网络预测之前必须要经过训练,通过训练使网络具有联想、记忆和预测的能力[16],其网络训练流程如图5所示。在网络训练之前,根据故障的13种类型分别进行编码,为方便后续故障分类及准确率的计算,采用13维单位矩阵对故障种类进行编码,每一行对应一种故障情况,具体的编码情况如表1所示。将原始数据通过WPT变换、PCA降维得到故障特征,将此故障特征作为BP神经网络的输入,相应的故障编码作为目标输出对神经网络进行训练。训练之后的网络即可用于故障的分类及定位。故障诊断流程图如6所示。
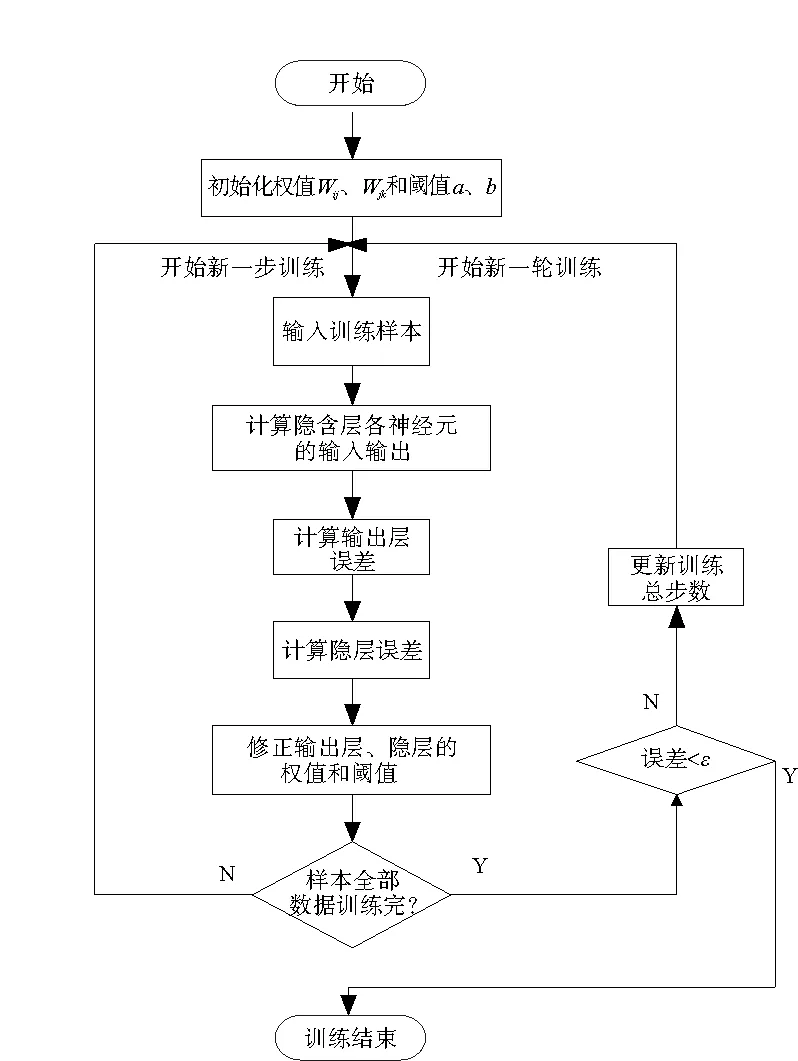
图5 BP神经网络训练流程图Fig.5 Flowchart of BP neural network training
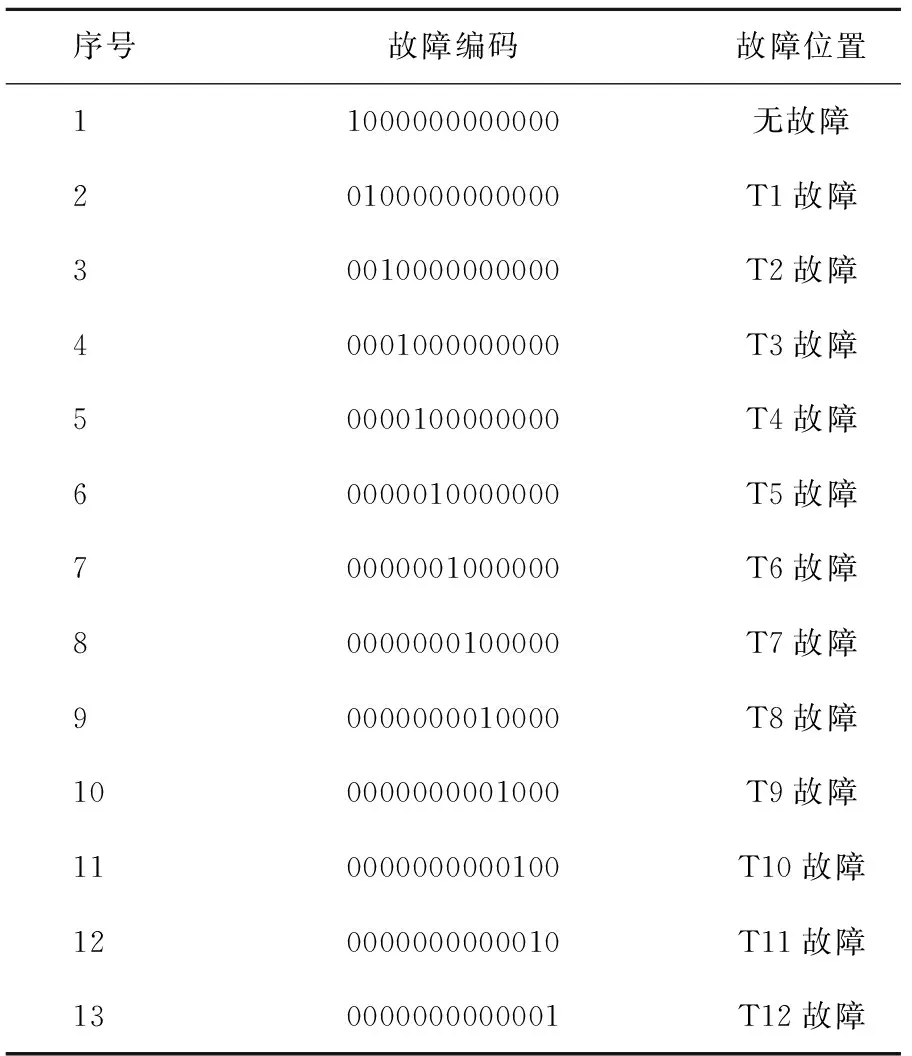
序号故障编码故障位置11000000000000无故障20100000000000T1故障30010000000000T2故障40001000000000T3故障50000100000000T4故障60000010000000T5故障70000001000000T6故障80000000100000T7故障90000000010000T8故障100000000001000T9故障110000000000100T10故障120000000000010T11故障130000000000001T12故障

图6 故障诊断流程图Fig.6 Flowchart of fault diagnosis
4 仿真与实验
基于以上分析,通过Matlab进行仿真实验,利用Simulink搭建仿真模型[17],仿真模型如图7所示。原始数据采集通过建立的Simulink仿真模型提取,采样间隔时间为0.000 1 s,采样时长为0.1 s,则每组采样数据是1 000个。为了提高实验的准确性,针对每种故障情况获取1 000组数据,13种故障情况共提取实验原始数据数量13×(1 000×1 000)个。
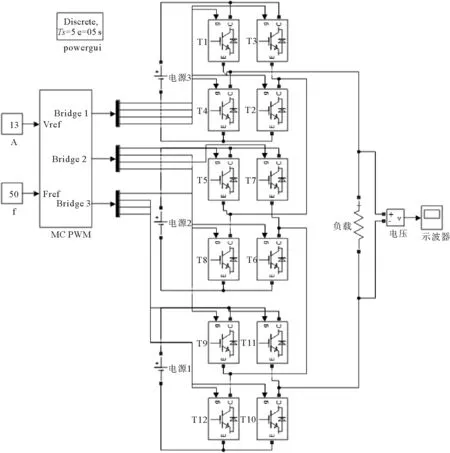
图7 七电平单相逆变器仿真模型Fig.7 Simulation model of seven-level single-phase inverter
对提取的13种故障特征数据进行三层小波包分解,分解过程中选取第三层分解小波包树类型为‘db1’,熵的类型为‘shannon’[18]。然后对小波包分解系数进行重构,提取各频带范围的信号求各频带信号的总能量,获取故障特征向量。采用三层小波包分解,因此原始1 000维数据通过小波包三层分解后分为8个节点,图8给出了13种故障类型经过三层小波包分解后8个节点重构系数波形图的其中2例。
根据公式(5)利用已得到的小波包重构系数计算出三层小波包能量,由于小波包能量值数值较大,求其能量值的算术平方根作为特征向量。通过公式(6)可以将各节点能量值的算术平方根构造为故障特征矩阵,该矩阵可以充分显示各故障类型的特征,这样原始数据经过上述变换后原始数据就变为13×(1 000×8)数据组。表2为13类故障经过三层小波包变化之后各节点能量值的算术平方根。
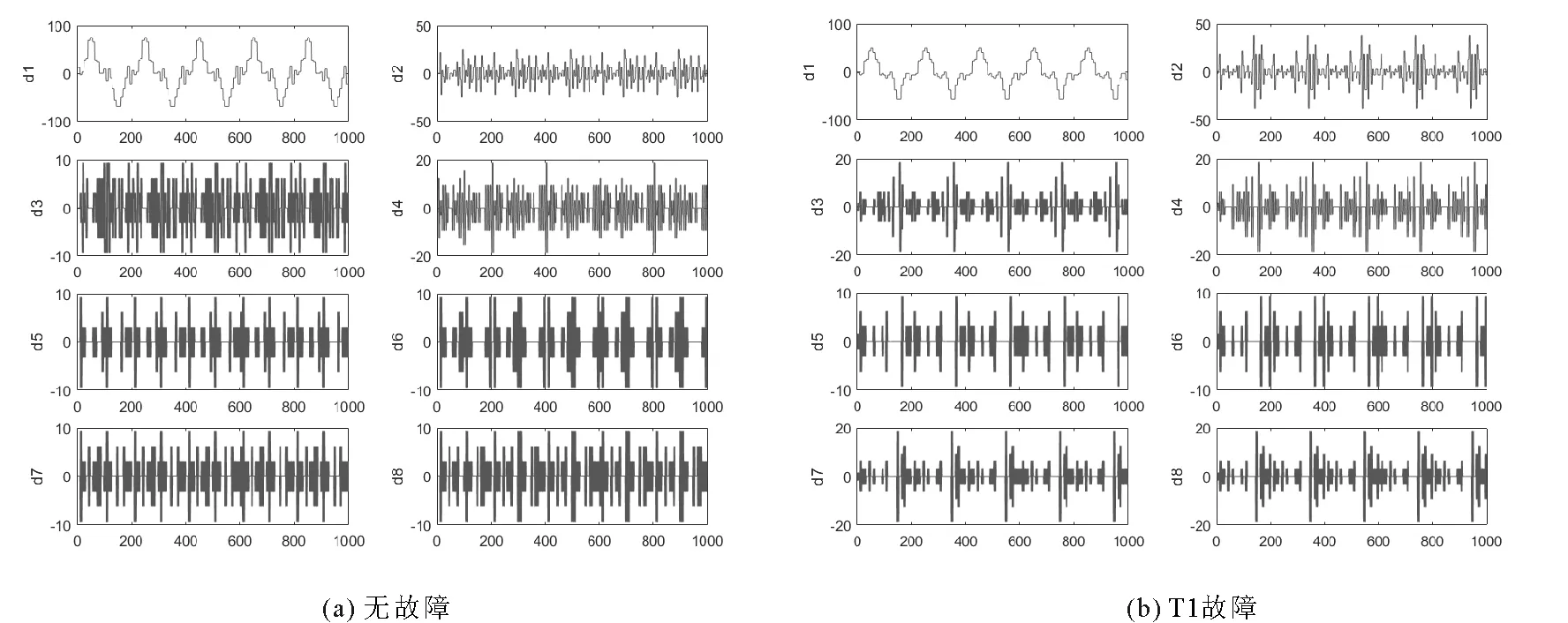
图8 各节点的小波包分解重构系数波形图Fig.8 Reconstruction coefficients waveform of WPT output for each node
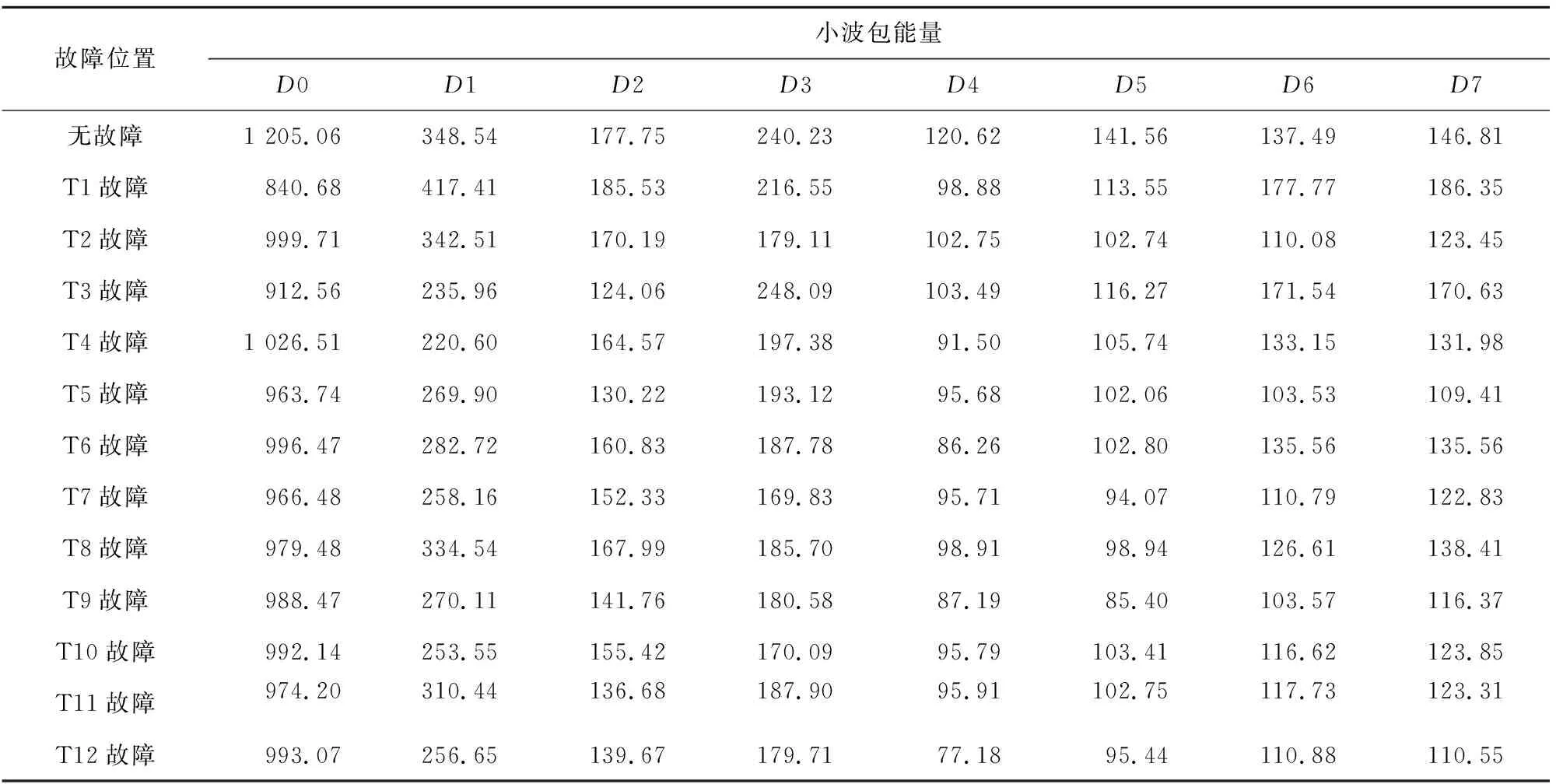
故障位置小波包能量D0D1D2D3D4D5D6D7无故障1 205.06 348.54 177.75 240.23 120.62 141.56 137.49 146.81 T1故障840.68 417.41 185.53 216.55 98.88 113.55 177.77 186.35 T2故障999.71 342.51 170.19 179.11 102.75 102.74 110.08 123.45 T3故障912.56 235.96 124.06 248.09 103.49 116.27 171.54 170.63 T4故障1 026.51 220.60 164.57 197.38 91.50 105.74 133.15 131.98 T5故障963.74 269.90 130.22 193.12 95.68 102.06 103.53 109.41 T6故障996.47 282.72 160.83 187.78 86.26 102.80 135.56 135.56 T7故障966.48 258.16 152.33 169.83 95.71 94.07 110.79 122.83 T8故障979.48 334.54 167.99 185.70 98.91 98.94 126.61 138.41 T9故障988.47 270.11 141.76 180.58 87.19 85.40 103.57 116.37 T10故障992.14 253.55 155.42 170.09 95.79 103.41 116.62 123.85 T11故障974.20 310.44 136.68 187.90 95.91 102.75 117.73 123.31 T12故障993.07 256.65 139.67 179.71 77.18 95.44 110.88 110.55
为了降低神经网络输入输出的维数,加快收敛速度,采用PCA主元分析法提取由小波包变换得到的8维特征向量。根据PCA分析法的原则,要保证各主元的累计贡献度达到85%以上,通过PCA算法对特征向量组进行降维,表3为经过PCA主元分析之后的特征数据。
根据公式(8)求取主元的特征值,根据特征值的占比求出各主元的贡献度,通过计算发现降维后前三组数据的贡献度分别为56.34%、30.39%和10.61%。根据主元分析的法则,当累计贡献度达到85%以上即可以表征原始数据的特征。因此分别选取累计贡献度达86.73%的二维主元和累计贡献度达97.34%的三维主元,并且通过MATLAB画出两种选取方法的故障特征散点图,如图9所示。由图可以较为明显看出,将故障特征降至二维时,大部分故障可以明显的分离开来,但是少部分故障集有重合的现象,而将故障降为三维时,所有故障基本上可以很好地分离。在下面的分类实验中,对两种情况分类的准确率进行了比较。
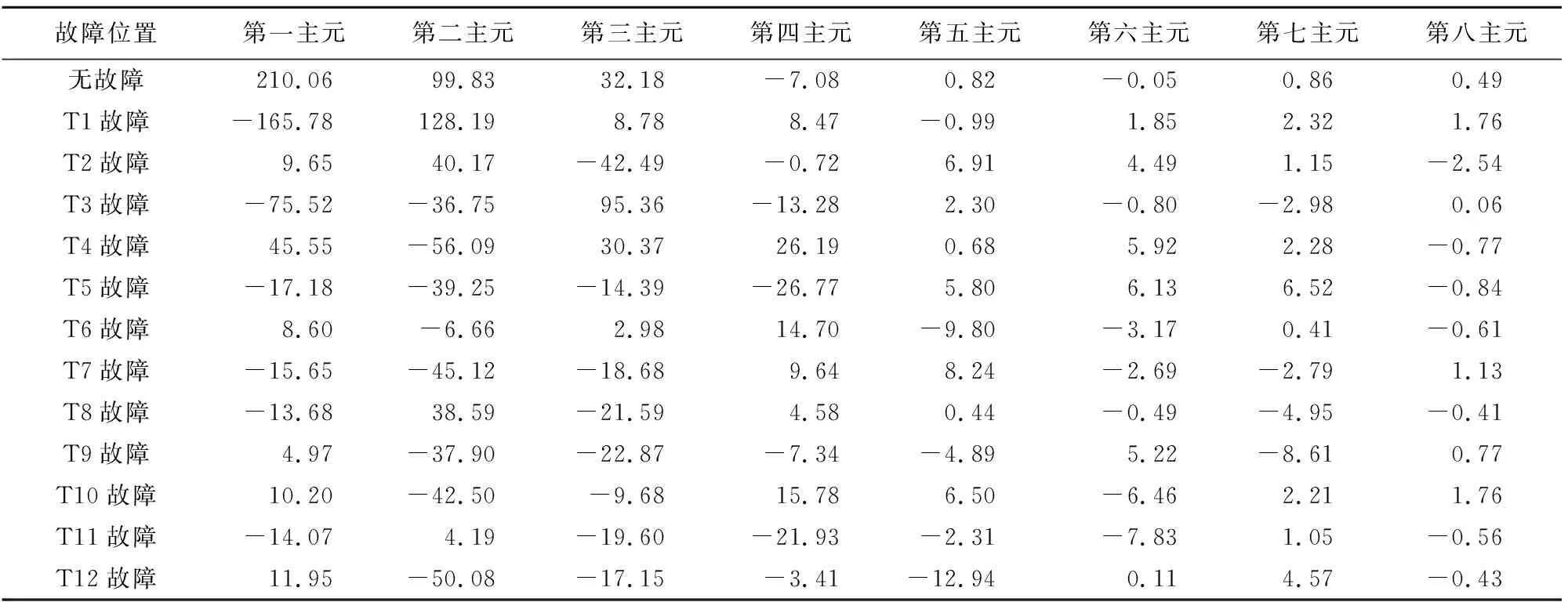
表3 PCA主元分析降维的特征数据Tab.3 Feature data of dimensionality reduction using principal component analysis

图9 故障特征散点图Fig.9 Scatter plot of fault features
最后,分别将提取的13种故障情况的900组数据作为BP神经网络的输入,相应的故障编码作为神经网络的输出,对神经网络进行训练。神经网络采用三层BP神经网络,输入层节点数为16,隐含层节点数为15,输出层节点数为13。其中节点传递函数采用‘tansig’函数,训练函数采用‘traingdx’。训练过程中最大迭代次数设置为10 000,学习率为0.01,网络设定要达到的误差值0.000 1。最后将13种故障情况的100组数据和相应的故障编码分别作为测试输入和期望输出输入神经网络中进行测试。
基于神经网络测试训练的随机性,进行多次测试训练得到测试结果并与FFT-BP[19]算法测试结果进行对比,其中FFT-BP方法是通过FFT提取原始数据信号的基波、3次谐波、5次谐波、7次谐波的幅值和相角作为特征向量。此外,试验直接将原始数据通过PCA降维进行分类的方法,但是在PCA降维阶段,在保证累计贡献度不低于85%的情况下,只能将维度降至160,为后续分类带来诸多麻烦,所以针对此问题此类方法不适用。对比测试结果如表4所示。

表4 准确率对比图Tab.4 Comparison of accuracy
从表4可以看出,通过FFT-BP方法能够得到较好的诊断效率,平均效率可达90%以上,但每次训练测试得到的准确率波动较大。运用WPT-PCA-BP方法将特征向量降至二维时,准确率和稳定性均较低,但是将特征向量降至三维时,效率得到很大的提升,准确率和稳定性均优于FFT-BP方法。图10为神经网络训练结果。
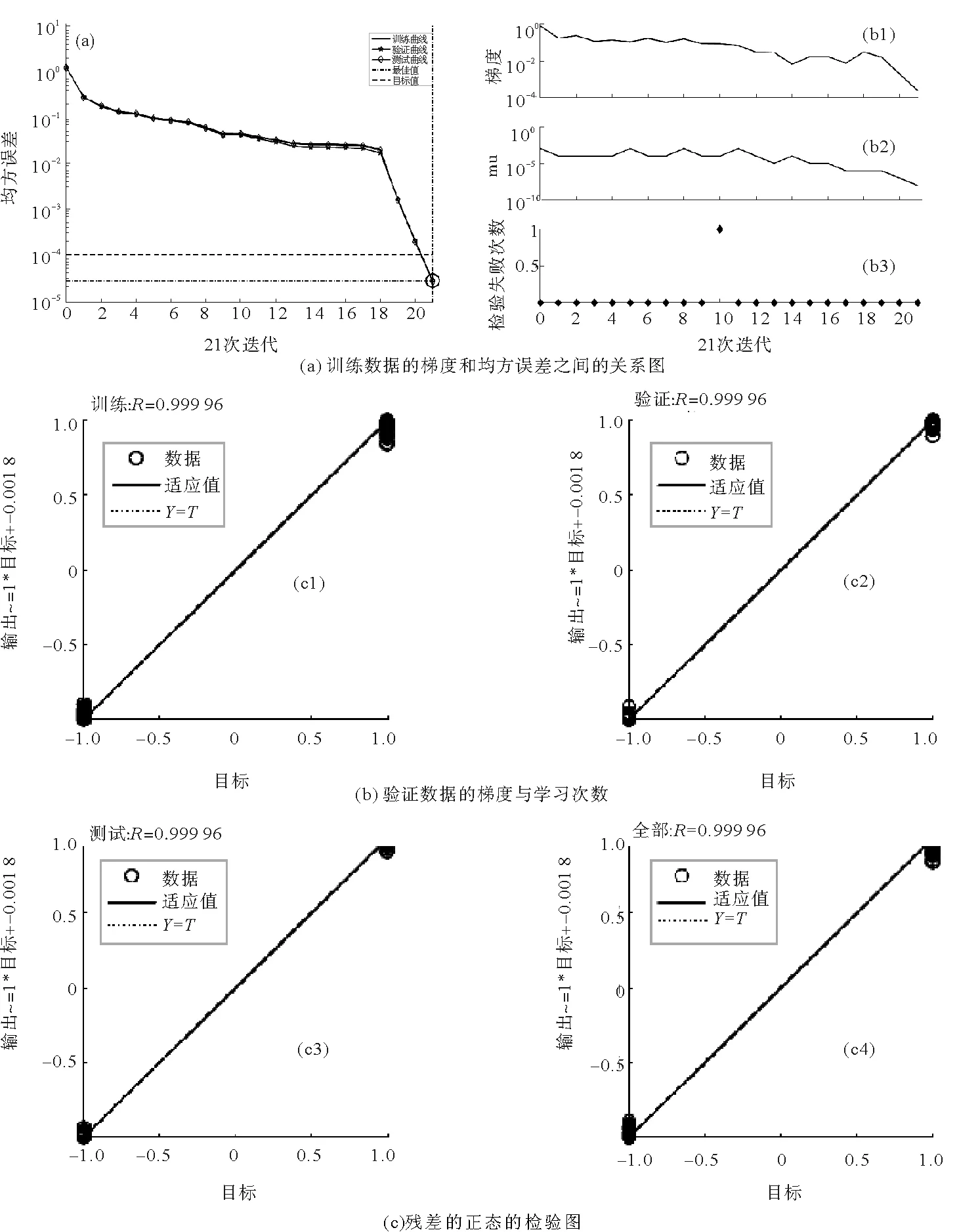
图10 神经网络训练结果图Fig.10 Neural network training results
5 结论
基于智能检测算法对级联H桥多电平模块化逆变器故障诊断进行研究,采用小波包变换对故障原始数据进行分解、重构最后得到能量谱组成故障特征。然后通过主元分析算法对故障特征进行主元提取达到降维的目的。最后将低维度的故障特征作为BP神经网络的输入,预先设定的故障编码作为神经网络的输出对网络进行训练,训练完成网络对故障进行分类检测。通过仿真实验对该方法进行了验证,结果表明该方法拥有很高的准确率,并且方法简单易于实现,能够很好地满足逆变器故障诊断的需要。

