非线性分数阶KdV-mKdV方程和mCH方程的孤波解

,

(内蒙古师范大学 数学科学学院, 内蒙古 呼和浩特 010022)

分数阶微分方程是广义的整数阶微分方程的经典形式。非线性分数阶偏微分方程在力学、工程学、电学、等离子体物理、生物学、控制论、经济学和金融等许多科学和工程领域中有着重要应用，受到极大关注，其研究工作日趋活跃[1]。首次积分法[2]、G′/G-展开法[3]、exp函数法[4]、扩展双曲正切函数法[5]、F-展开法[6]等诸多方法被先后应用于求解非线性分数阶偏微分方程。2008年至2009年，Biswas、Triki和Wazwaz[7]提出了求解非线性分数阶偏微分方程另一种方法——拟设法，并用该方法给出KdV和mKdV等方程的亮孤子解和暗孤子解。2015年，Guner等[8]求解了时空分数阶Boussinesq方程的亮孤子解和单孤子解。2016年，Guner和Bekir[9]利用拟设法求解了时空分数阶mBBM方程的亮孤子解和暗孤子解，同一年，Korkmaz[10]利用拟设法求解了时空分数阶EW和mEW方程的单孤子解。2017年，Guner和Bekir[11]利用拟设法求解了时空分数阶mEW方程的暗孤子解。但他们只处理了包含单独的sech函数或tanh函数的情形，未考虑包含sech和tanh函数的乘积项的情形。本研究把拟设法推广应用到出现sech函数与tanh函数的乘积项的情形，并借助修正的黎曼-刘维尔导数给出时空分数阶KdV-mKdV[12]方程和Modified Camassa-Holm方程的精确孤波解。

修正的α阶黎曼-刘维尔定义为[13]

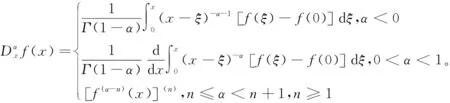
(1)

其中f(x)表示连续函数，Γ(α)表示Gamma函数，具有以下形式[14]

(2)

或者

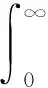
(3)

修正的黎曼-刘维尔导数具有许多有用的性质，如

(4)

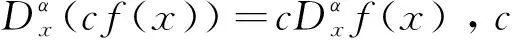
(5)

(6)

(7)

考虑具有以下形式的非线性时空分数阶偏微分方程

(8)

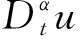
分数阶微分方程可以通过变换

(9)

转化为整数阶微分方程，这里k和c为非零常数。在计算过程中使用分数阶导数的链法则

(10)

把式(4)、(9)和(10)代入式(8)中，可以把式(8)转化为以下形式的非线性常微分方程

Q(U,U′,U″,U′″,…)=0,

(11)

其中,Q是关于U(ξ)及其各阶导数的多项式。

本研究旨在利用拟设法研究时空分数阶KdV-mKdV方程和Modified Camassa-Holm方程的孤波解。

1 时空分数阶KdV-mKdV方程的孤波解

考虑方程时空分数阶KdV-mKdV方程

(12)

其中，μ和δ为任意常数。

为了求解方程(12)的亮孤子解，将使用以下形式变形：

u(x,t)=U(ξ),

(13)

(14)

其中，c为非零任意常数。

将式(4)、(10)和(14)代入方程(12)，方程(12)可化为以下形式常微分方程

-cU′+μUU′+δU2U′+U′″=0,

(15)

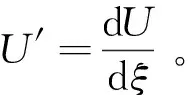
作以下假设

U(ξ)=Asechpξ,

(16)

其中，A为任意非零常数。在求解方程(12)的亮孤子解的过程中将确定p的取值。

通过方程(14)和(16)可以得到

(17)

U2(ξ)=A2sech2pξ。

(18)

把方程(16)～(18)代入方程(15)中，则得到

cApsechpξtanhξ-Ap3sechpξtanhξ-μA2psech2pξtanhξ

-δA3psech3pξtanhξ+Ap(p+1)(p+2)sechp+2ξtanhξ=0。

(19)

进一步化简得到

cAp-Ap3-μA2psechpξ-δA3psech2pξ+Ap(p+1)(p+2)sech2ξ=0。

(20)

平衡方程(20)中的sech2pξ项与sech2ξ项，则得2p=2,即

p=1。

(21)

将p=1代入方程(20)后，令sech2ξ的系数和为零，则得到

Ap(p+1)(p+2)-δA3=0,

(22)

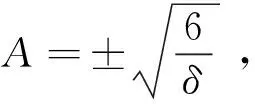
在方程(20)中，令sechξ的系数为零，则得到μ=0；令常数项为零，则有

cAp-Ap3=0,

(23)

由此解出c=1。

因此，得到方程(12)的如下形式的亮孤子解

(24)

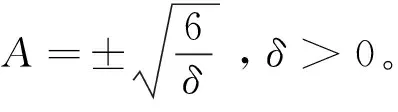
再假设方程(12)有以下形式的孤波解

U(ξ)=Acschpξ,

(25)

其中A为任意非零常数。在求解方程(12)的孤子解的过程中将会确定p的取值。

因此，通过方程(14)和(25)可以得到：

(26)

U2(ξ)=A2csch2pξ。

(27)

把方程(25)至(27)代入方程(15)中,得到

-cApcschpξcothξ-μA2pcsch2pξcothξ-δA3pcsch3pξcothξ
-Ap3cschpξcothξ-Ap(p+1)(p+2)cschp+2ξcothξ=0 ,

(28)

进一步化简得到

-(c+p2)cschpξ-μAcsch2pξ-δA2csch3pξ-(p+1)(p+2)cschp+2ξ=0。

(29)

平衡(29)中csch3pξ项与cschp+2ξ项,则得3p=p+2，即

p=1。

(30)

将p=1代入方程(29)后令csch3ξ的系数和为零，则得到

(p+1)(p+2)+δA2=0,

(31)

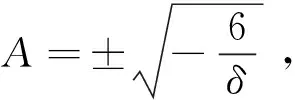
在方程(29)中，令csch2ξ的系数为零，则得到μ=0；令cschξ为零，则有

-(c+p2)=0，

(32)

并由此解出c=-1。

因此，方程(12)具有下面的奇异孤波解

(33)

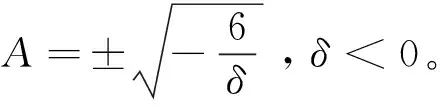
2 时间分数阶Modified Camassa-Holm方程的孤波解

考虑方程时间分数阶Modified Camassa-Holm(mCH)方程

(34)

其中，0<α<1，β>0，k∈R。

为了求解方程(34)的亮孤子解，将使用以下形式变形：

《企业会计准则》重新制定关于企业内部研发费用的会计处理，批准其符合标准可资本化。促进了无形资产的会计处理和信息披露的标准化。然而，实际运用中，行业标准缺乏标准型和统一性，企业往往依赖主观判断和内部未来计划标准去进行实际会计操作，研发支出费用化或资本化不仅从一方面可说明企业会计处理的谨慎性，其装化为无形资产可调整利润，无形中提高了市场乃至社会对于相关信息的披露要求。

u(x,t)=U(ξ)，

(35)

(36)

其中，c为非零任意常数。

将式(4)和方程(10)、式(36)代入方程(34)，方程(34)可化为以下形式常微分方程：

-clU′+2kU′+βU2U′+clU′″=0，

(37)

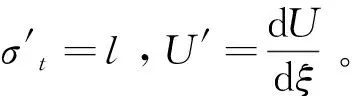
作以下假设

U(ξ)=Asechpξ，

(38)

其中，A为任意非零常数。在求解方程(34)的亮孤子解的过程中将确定p的取值。

因此，通过方程(38)可以得到：

(39)

U2(ξ)=A2sech2pξ。

(40)

把方程(38)～(40)代入方程(37)中，则得到：

-Apsechpξtanhξ(-cl+2k+βA2sech2pξ)-Aclp3sechpξtanhξ+

(41)

进一步化简得到：

-(2k-cl+clp2)sechpξ-βA2sech3pξ+cl(p+1)(p+2)sechp+2ξ=0,

(42)

平衡方程(42)中的sech3pξ项与sechp+2ξ项，得3p=p+2,即

p=1。

(43)

将p=1代入方程(42)，令sech3ξ的系数和为零，则得

6cl-βA2=0。

(44)

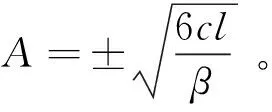
在方程(42)中令sechξ的系数为零，则得到k=0。

因此，得到方程(34)的如下形式的亮孤子解

(45)

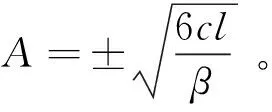
再假设方程(34)有以下形式的孤波解

U(ξ)=Acschpξ,

(46)

其中，A为任意非零常数。在求解方程(34)的孤子解的过程中将确定p的取值。

因此，通过方程(36)和(46)可以得到：

(48)

把方程(46)～(48)代入方程(34)中,得到

-Apcschpξcothξ(-cl+2k+βA2csch2pξ)-Aclp3cschpξcothξ

-Aclp(p+1)(p+2)cschp+2ξcothξ=0 ,

(49)

进一步化简得到

(cl-2k-clp2)cschpξ-βA2csch3pξ-cl(p+1)(p+2)cschp+2ξ=0,

(50)

平衡(50)中csch3pξ项与cschp+2ξ项,则得3p=p+2即

p=1。

(51)

将p=1代入方程(50)，令csch3ξ的系数和为零，则得到

βA2+6cl=0。

(52)

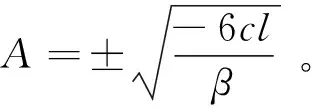
在方程(50)中令cschξ的系数为零，则得到k=0。

因此，方程(34)具有下面的奇异孤波解

(33)

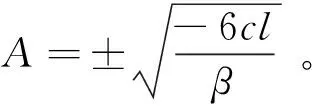
3 结论

利用拟设法求解时空分数阶KdV-mKdV方程和时间分数阶mCH方程的孤波解，包括亮孤子解和奇异孤波解，表明拟设法是求解时空分数阶偏微分方程的有效方法。拟设法也适用于求其他分数阶偏微分方程的孤波解，且当拟设法中设U(ξ)=Atanhpξ时能够给出某些分数阶非线性方程的暗孤子解。