基于运动学的机器人轨迹规划研究

吴秀利，张开生，陈朋威

(陕西科技大学 陕西 西安 710021)

0 前言

工业机器人是一个复杂的多刚体系统，且机器人工作是一个动态的过程[1]。机器人要获得高速和高精度的运动性能就需要在运动时间和轨迹平滑性方面达到最优[2]；为此对多目标轨迹优化的研究较多，基本分为时间最短[3-4]、能量最小[5]和最小脉动[6]。但是所有的优化都是在已知轨迹的基础上进行的。关节空间轨迹规划在减小关节突变，避免奇异点和满足运动约束方面有很大优势。

为此建立机器人运动方程[7]及开展机器人关节空间的轨迹规划，并研究基于运动规划的关节机器人轨迹特性是机器人轨迹跟踪控制的前提和基础[8]。

1 六自由度工业机器人的运动学建模

根据串联关节机器人机构特点，采用Denavit-Hartenberg方法建立连杆坐标系，机器人原点建立笛卡尔坐标系如图1所示，机器人的D-H参数、各关节运动范围和运动速度边界值表1所示。

图1 六关节机器人连杆坐标系

编号连杆长度/mm连杆扭角/(°)关节偏移/mm初始转角/(°)各轴最大速度/(°)·s-1139.8590002252279.90090150371.790002754090313041250-90090450681.6000720

建立D-H模型并进行正向运动学推导。求解机器人末端坐标系到基坐标系的齐次变换矩阵随各关节轴的变化关系。

(1)

将各连杆D-H参数带入得：

(2)

从末端坐标系依次向前做齐次变换得末端坐标系到基坐标系的变换关系：

(3)

位姿矩阵参数较为复杂，将其简要表达为

(4)

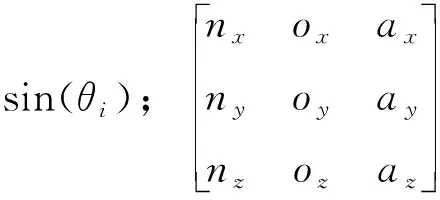
2 实例计算及仿真

以6关节3 kg机器人为研究对象，依据机器人机构和参数(图1和表1)，机器人末端满足图9所示的矩形轨迹，通过虚拟样机技术[9-10]，建立基于ADAMS的机器人虚拟样机模型如图2所示，对机器人关节空间进行逆运动学计算并对计算数据进行数据拟合，使拟合数据用于机器人关节空间轨迹规划，机器人关节空间运动规划结果图3～图8所示，得出机器人6个关节的速度及加速度随时间运行的特性。分析机器人各轴加速度数据，其加速度均未出现跃变，轨迹运行连续且比较平稳。

图2 机器人虚拟样机模型

图3 机器人1轴关节空间轨迹规划

图4 机器人2轴关节空间轨迹规划

图5 机器人3轴关节空间轨迹规划

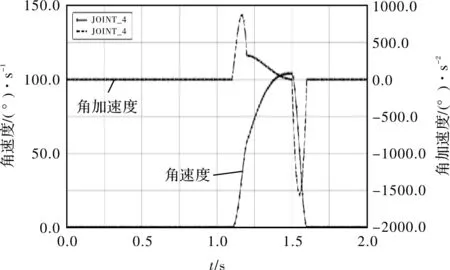
图6 机器人4轴关节空间轨迹规划

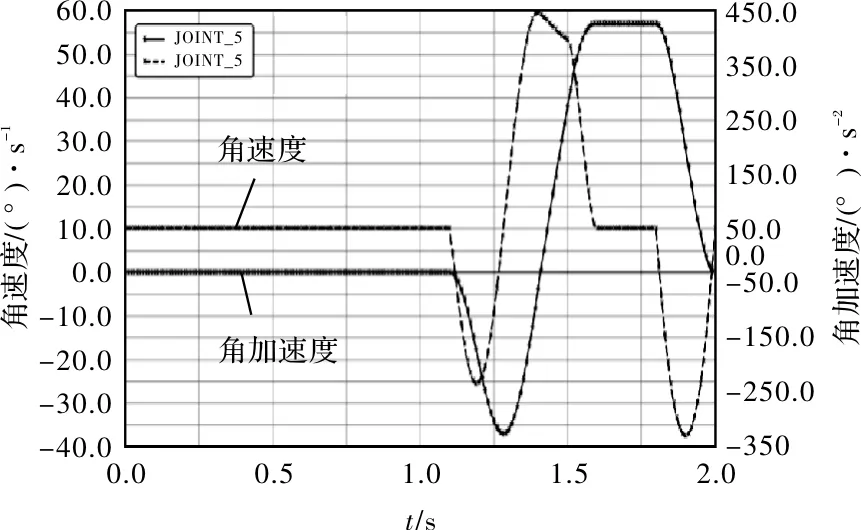
图7 机器人5轴关节空间轨迹规划

图8 机器人6轴关节空间轨迹规划

3 实验

通过机器人位置稳定时间和位置超调量试验来评估机器人关节空间轨迹规划的特性，实验条件如表2所示，机器人末端运行轨迹图9所示。测量单元图10所示，机器人轨迹测试平台如图11。

表2 实验条件

图9 试验轨迹

图10 机器人测量单元

图11 机器人轨迹规划实验平台

机器人各轴按照图3～图8所示轨迹运行，机器人末端安装TMAC，使用激光跟踪仪实时测量机器人末端运行轨迹，经数据分析，3次测量到达P0点时采样点至实到位置的距离变化分别如图12、图13和图14所示。

图12 第1次采样点至实到位置的距离变化

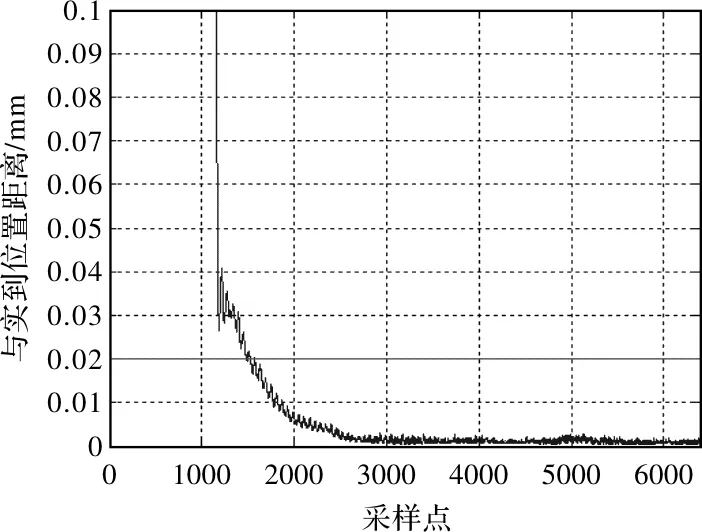
图13 第2次采样点至实到位置的距离变化

图14 第3次采样点至实到位置的距离变化

4 结束语

机器人的设计重复定位精度值0.02 mm为门限带值，由图12和图13及图14可知，机器人末端到位进入门限带后未出现超调振荡现象，说明机器人末端的到位方式为过阻尼接近方式，其位置稳定时间和位置超调量均为零。实验结果表明本文运动学轨迹规划方法的有效性和可参考性。