一种领航-跟随型多移动机器人编队控制方法*

王荪馨，王经国

(1.西安理工大学信息技术与装备工程学院，西安 710082；2.烽火通信科技股份有限公司，武汉 430205)

0 前言

多移动机器人编队是多无人系统技术领域的一个重要分支，在联合侦查、群体盯梢、协作救援、合作搬运、传感网络等军事和民用领域具有广阔的应用背景。多移动机器人编队是多台移动机器人自主协作组成一个较为精准的编队或构型以完成特定的作业任务，并在执行作业任务、目标跟踪、躲避障碍物时尽可能保持预期的编队几何队形不变。由于受传感器感知范围、单体作业半径、设备搭载能力、通讯距离等因素制约，在执行大范围、长距离、动态复杂等环境下的复杂作业任务时，传统单台机器人难以胜任。因此，多移动机器人编队则成为解决这类复杂问题的有效途径。

目前，多移动机器人编队控制方法主要包括：行为法(Behavior-based)、虚拟结构法(Virtual-structure)和领航-跟随法(Leader-follower)。基于行为的多机编队方法无法准确描述系统整体行为，且不能保证系统控制的稳定性；而虚拟结构法则存在系统灵活性不足的缺陷；领航-跟随型编队控制法[1]具有数学分析简单、易保持队形、通信压力小等优点，被广泛应用于多无人系统编队，如：野外作战系统编队、无人机编队和水下舰船编队等诸多应用领域。

领航-跟随(leader-follower)型编队控制方法在具体执行多机编队作业任务时，领航机器人(Leader)负责目标跟踪、路径规划、主动避障等任务，而跟随机器人(follower)负责主动跟随领航者的运动轨迹，并尽可能保持预定的理想编队几何队形。文献[2]将多机编队控制问题划分为轨迹跟踪、机器人控制和队形保持3个子问题，通过控制相对距离-相对角度、相对距离-相对距离来实现多机编队控制。文献[3]为了自主形成期望的编队队形，采用一种综合的轨迹跟踪控制方法来确保系统跟踪误差稳定。针对复杂环境下的领航-跟随型编队控制问题，文献[4]采用模糊控制方法来确保多机编队系统自主避障和保持队形，文献[5]提出了一种模糊逻辑控制方法来对非完整轮式移动机器人进行队形控制，文献[6]提出了一种综合运动学和计算力矩的输出反馈控制率来完成预期几何队形的自主控制。

综上所述，在领航-跟随型编队控制研究领域，现有研究较好地解决了确定性目标和静态环境下的编队控制、轨迹跟踪等问题，但针对未知复杂环境条件下的多机编队研究甚少，特别是领航机器人如何在线进行路径规划、实时自主避障等方面亟待进行更深入研究。为此，本文针对在未知复杂环境条件下领航-跟随型编队控制中的路径规划、编队形成和队形保持3类问题，采用人工势场法进行在线局部路径规划，运用滑膜控制方法自主调节跟随机器人的实时位姿，以确保在无碰撞的条件下完成从初始位置到目标位置的多机编队运动。

1 领航-跟随型编队控制问题及其解决方案

1.1 领航-跟随型编队控制问题

在领航-跟随型编队控制问题中，选定一台机器人作为领航者，主要负责整个编队的路径规划任务，而其余机器人则被视为跟随者。跟随机器人负责实施跟踪领航者，并尽可能与领航机器人之间保持队形所需的距离和角度，从而确保整个多机编队按照预期的理想编队队形进行无碰撞运动，并最终到达目标位置，其运动场景如图1所示。

图1 领航-跟随型多机编队问题场景

1.2 领航-跟随型编队控制的整体解决方案

针对领航-跟随型编队控制问题，本文提出了图2所示的整体解决方案。该解决方案包括3个主要阶段：

(1)初始化阶段：给定多机编队队形任务，确定领航机器人和跟随机器人角色，确定各机器人的初始位姿，建立领航-跟随机器人编队运动学模型。

(2)领航机器人在线路径规划：在任意i时刻，领航机器人依据人工势场法计算i+1时刻的自身位姿和跟随机器人的理想位姿；

(3)跟随机器人轨迹跟踪：在i+1时刻，各跟随机器人依据给定的理想位姿，运用滑膜运动控制器实时调节该时刻机器人的线速度和角速度，从而确保当前时刻跟随机器人保持预期几何队形并跟随领航机器人进行编队运动。

图2 领航-跟随型编队控制整体解决方案

2 领航-跟随型编队控制的运动学模型

2.1 轮式移动机器人的运动学模型

本文采用轮式移动机器人，而轮式移动机器人的无滑动滚动特征决定了系统满足非完整约束条件。因此，对于具有非完整性约束的双轮移动机器人，其运动学模型如图3所示，表达式为

图3 双轮驱动的移动机器人运动学模型示意图

式中，(xc,yc)是机器人的中心坐标；θ是车身轴线与x轴的夹角；(v,ω)T为移动机器人的2个主要控制参数，其中，v、ω分别是机器人的线速度和角速度。

2.2 领航-跟随型编队控制的运动学模型

以单机运动学模型为基础，图4给出了包含三角形编队队形、三台机器人、双轮移动机器人的领航-跟随型编队控制运动学模型。在领航-跟随型编队控制问题中，编队的主轨迹由领航机器人自主规划确定，队形形成和保持则由跟随机器人的期望位姿参数来确定。

图4 领航-跟随型编队控制的运动学模型示意图

图4中，R1为领航机器人，R2和R3为2台跟随机器人，而Rv则是R2为了形成和保持预期队形而假设的虚拟机器人；R1和Rv之间期望的距离和方位角为(ρ,φ)T。结合R1的位姿并经几何坐标变换，即可得到Rv的期望位姿。

式中，R1位姿为(x1,y1,θ1)T，R2期望位姿为(xv,yv,θv)T。

在领航-跟随编理想控制条件下，Rv和R1的线速度和角速度应该保持相等(即vv=v1，ωv=ω1)。而R2的跟踪位姿误差表示为

(xe,ye,θe)T=(x-xv,y-yv,θ-θv)T

3 基于改进型人工势场法的领航机器人在线局部路径规划

在领航-跟随型编队控制中，首先需要解决承担整个编队引领任务的领航机器人的路径规划问题，即：领航机器人进行在线局部路径规划，引导其后的跟随机器人，形成和保持预期的编队队形，从起点到目标点进行无碰撞的编队运动，从而完成既定的作业任务。

人工势场法将机器人的实际运动空间抽象为物理中的势场，机器人在该势场中同时受目标引力场和障碍物斥力场的共同作用。通过人工势场法这类在线局部路径规划方法，可以引导整个多机编队在运动过程中实时躲避障碍物并顺利抵达目标位置。因此，相对于目前大多数路径规划算法，由于人工势场法具有结构简单、依赖信息少等优势，特别是该方法在避障方面的独特优势，使得非常适合未知复杂环境下的在线局部路径规划任务。然而，人工势场法所具有的引力和斥力叠加效应使得其存在“目标不可达”的弊端[7]。

为此，针对领航机器人在复杂未知环境下的在线路径规划需求，以及人工势场法自身存在的目标不可达问题，本文在标准人工势场法[7]的基础上，提出了一种改进型人工势场法如图5所示。改进型人工势场法使得目标点成为全局势场中的最小点，而斥力场在目标位置附近尽可能趋近于零。

图5 改进型人工势场法示意图

领航机器人R1在外部环境中受到的总势场为Utotal(X)=Uatt(X)+Urep(X)，而领航机器人在总势场中对应的合力Ftotal(X)为Ftotal(X)=Fatt(X)+Frep(X)。

在运用人工势场法进行在线路径规划时，领航机器人根据Ftotal(X)的方向和自身的行驶速度v，来计算下一时刻领航机器人和跟随机器人的轨迹坐标，从而引导整个编队进行无碰撞运动。以下结合图5对总势场计算和合力计算2个公式中涉及的变量进行详细解释。

在图5中，领航机器人R1的位置表示为X=(x,y)，则R1和目标之间的引力势函数为

式中，Xg为目标位置，(X-Xg)为机器人R1和目标之间的距离；Katt为引力位置增益系数，则领航机器人在引力场中受到目标的引力为Fatt(X)=-Uatt(X)=-katt|X-Xg|。

考虑到机器人与目标之间的相对距离，R1和障碍物之间的斥力势函数为

式中，(X-Xg)为机器人和目标之间的相对距离；(X-X0)为机器人和障碍物之间的距离；η是斥力位置增益系数；ρ0是障碍物的影响距离；n为任意实数。

与标准人工势场法中的斥力势函数相比较，这里的改进型人工势场法的斥力函数计算利用了机器人与目标之间的相对距离，即：当机器人接近目标点时，(X-Xg)逐渐变小，相应的斥力场也随之减小，从而保证了整个势场仅在目标点Xg最小。因此，机器人在势场中对应的斥力计算为

Frep(X)=-

其中，

4 基于滑膜运动控制的跟随机器人轨迹跟踪方法

通过基于人工势场法的领航机器人在线路径规划，即可得到整个编队的运动轨迹。编队系统的主要任务是设计各跟随机器人的运动控制器，依此引导跟随机器人按照预期的理想位姿和领航机器人形成并保持既定的编队队形。在多机编队轨迹跟踪控制器设计方法中，目前主要包括：自适应控制法、非线性状态反馈控制法、反步控制法和滑膜控制法等。与其他控制方法相比较而言，滑膜控制方法中的滑膜模态设计和系统参数与扰动无关，而且具有较好的鲁棒性[8]。因此，本文引入滑膜运动控制器来执行跟随机器人的轨迹跟踪控制任务。

在图4所示的领航-跟随型编队控制运动学模型中，采用人工势场法可以确定出领航机器人的位姿(x,y,θ)，为了形成和保持预期编队队形，各跟随机器人需要实时保持和领航机器人之间的距离l和方位角φ。而通过跟随机器人的运动控制器来实时调节其线速度和角速度(v,ω)T，从而尽可能确保各个跟随机器人的实际位姿与其理想位姿的误差趋近于零。针对跟随机器人的轨迹跟踪控制器设计问题，结合所提出的领航-跟随型编队控制的运动学模型，采用基于双幂指数趋近率的滑膜运动控制器为

这里仍然结合图4对滑膜运动控制器进行说明。假设在i时刻，领航机器人的位姿为(x1,y1,θ1)，由于跟随机器人与领航机器人应保持距离l和观测角φ，经过坐标变换即可求得跟随机器人在全局坐标系下的理想位姿(xv,yv,θv)为

跟随机器人的理想位姿对应的虚拟机器人的运动学方程为

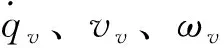
依据文献[9]，跟随机器人R2从位姿(x2,y2,θ2)T移动到虚拟机器人位姿(xv,yv,θv)T的位姿误差方程为

通过反步法并结合Lyapunov定理，求得切换函数为

根据双幂次趋近控制率，使得s1→0，s2→0，实现xe收敛到0且θe收敛到-arctan(vrye)，从而实现ye→0，θe→0。根据文献[8]，求得跟随机器人R2的滑膜运动控制器为

则在i+1时刻，根据滑膜运动控制器求得跟随机器人R2的位姿(x2,i+1,y2,i+1,θ2,i+1)T为

x2,i+1=x2,i+t·v2,i·cos(θ2,i+1+t·ω2,i)

y2,i+1=y2,i+t·v2,i·sin(θ2,i+1+t·ω2,i)

θ2,i+1=θi+t·ω2,i

其中，t为时刻i和时刻i+1的时间间隔。

依据该计算方法，同理可计算得到的跟随机器人R3的滑膜运动控制器。

综上所述，在领航-跟随型编队控制问题中，领航机器人基于改进型人工势场法进行在线路径规划，从而确定出从起点到目标点的无碰撞路径；编队中各个跟随机器人在滑膜运动控制器的自主调节下促使多机形成并保持既定编队队形，并以此队形运动至目标点。

5 领航-跟随型编队控制方法的仿真实验

为了验证该领航-跟随型编队控制方法的有效性，实验选用三角形编队队形、3台移动机器人，在两类实验场景条件下，运用MATLAB软件对编队控制方法中的在线路径规划和轨迹跟踪控制方法进行仿真验证。

(1)实验场景1。在无障碍物环境下，领航

机器人R1采用基于改进型人工势场法进行在线局部路径规划，两台跟随机器人R2和R3采用滑膜运动控制器。三台机器人从起始点到目标点进行三角形编队运动。仿真实验结果如图6～图8所示。

从图6可知，三台机器人从初始的随机状态，经过滑膜运动控制器对两台跟随机器人的运动控制，快速形成了预期的三角形编队队形，两台跟随机器人自主跟随领航机器人以稳定的编队队形从起始点顺利到达了目标点。另外，从图7和图8可知：两台跟随机器人能快速移动到理想位姿，并以较小运动误差(接近于0)保持编队队形进行整体移动。

图6 实验场景1环境下领航-跟随编队在线路径规划实验结果

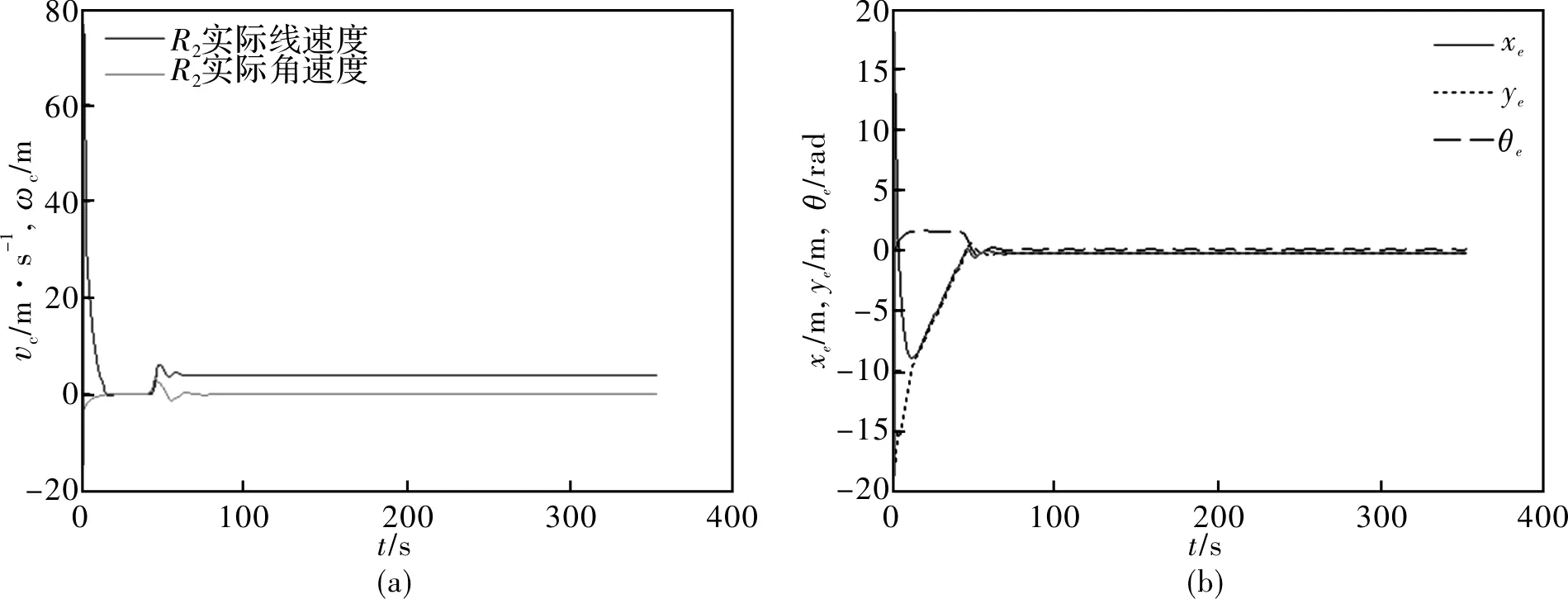
图7 实验场景1环境下跟随机器人R2的线速度、角速度和运动误差

图8 实验场景1环境下跟随机器人R3的线速度、角速度和运动误差

(2)实验场景2。在静态障碍物环境下，运用本文提出的在线路径规划和滑膜运动控制器进行编队实验。实验结果如图9～图11所示。

从图9可知，在障碍物环境下，领航机器人仍能规划出一条无碰撞路径，并带领2台跟随机器人以较小的队形误差从起始点顺利抵达目标点。从图10和11实验结果可知：由于滑膜运动控制器的实时调节机器人的位姿，在路线中存在较多障碍物的环境下，仍能通过运动控制器的自我调姿，并以较小的运动误差保持预期的编队队形。

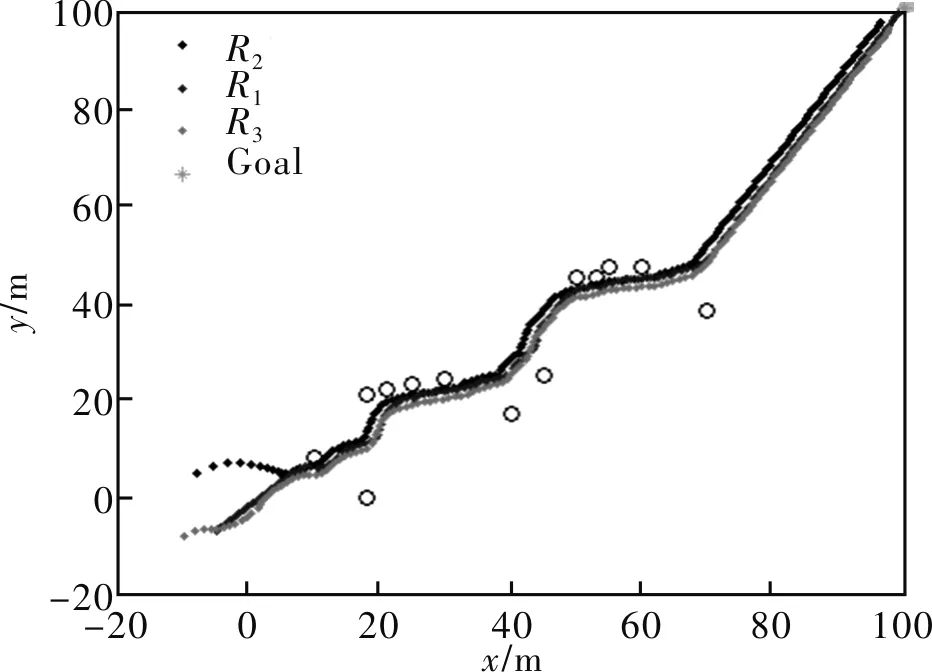
图9 实验场景2环境下领航-跟随编队在线路径规划实验结果

图10 实验场景2环境下跟随机器人R2的线速度、角速度和运动误差

图11 实验场景2环境下跟随机器人R3的线速度、角速度和运动误差

6 结论

本文将改进型人工势场法和滑膜运动控制有机融合，提出了一种一体化、集成化的领航-跟随型编队控制方法，有效解决了领航机器人的在线路径规划和跟随机器人的轨迹跟踪两类问题，最后的两类工况仿真实验也验证了该方法的可行性和有效性。这种集成了在线路径规划和轨迹跟踪的一体化多机编队控制方法，有助于实现多移动机器人编队成形、队形保持和在线避障等作业任务。该方法在多无人系统自主编队、多移动机器人协作搬运、智慧物流等领域具有潜在应用价值。后续将以集成化的领航-跟随型编队控制方法为核心，设计制作移动机器人实物，并在接近实际工况环境下进行实证研究。