基于二分法的自动驾驶仪参数优化设计

谢金龙 吴 璋 文世珍 胡 洲

（四川航天系统工程研究所，成都 610100）

导弹的自动驾驶仪即导弹的姿态控制系统，根据制导系统给出的指令信号控制导弹的姿态运动，保证其在飞行中具有足够的机动性和稳定性，从而确保导弹飞行的安全。自动驾驶仪的主要作用包括保证弹体的稳定性、优化弹体的阻尼特性、提高弹体的机动性能，以及提高弹体的抗干扰能力。

自动驾驶仪的设计方法主要分为经典控制和现代控制。经典的设计方法以经典控制理论为基础，将系统简化为单输入单输出结构。在简化模型的基础上，利用传递函数描述系统特性，结合时域响应法、频域响应法等方法保证系统具有良好的稳定性和快速性。现代控制理论成果主要包含动态逆、滑模变结构、神经网络、状态Ricatti方程等。

Nesline等人在1979年提出了一种最优/经典综合设计法，他的主要想法是通过对系统传递函数的频率特性提供约束，限制目标函数中增益系数的取值范围，从而达到最优的控制效果。Mracek等人则系统地提出了应用最优控制理论设计自动驾驶仪的方法原理。

经典控制理论设计的自动驾驶仪能够直观地了解所选特征点的时域及频域特性，因此它在工程实践中是战术导弹自动驾驶仪设计的主要方法。但是这种方法需要花费大量的时间和精力调试，设计过程繁琐，所以找到一种快速的参数设计方法很有必要。

自动驾驶仪设计过程中涉及许多新兴的方法，如保护映射、极点配置等。当系统传递函数阶次较低时，极点配置可以较好地实现频域设计。当系统传递函数阶次大于二阶时，往往需要用到一些经验公式，但是这些经验公式反解得到的增益往往不能很好地稳定系统。

当系统模型比较复杂时，将传递函数的某项频域指标（如幅值裕度）作为性能指标函数再得到性能指标函数关于增益参数的变化曲线，通过选取合适的增益边界范围，就可以应用二分法逼近得到相应的参数。对得到的参数进行优化，就可以得到满足其他约束条件的最优解。二分法可以实现计算机代替人为调参，有效提高了设计人员的工作效率。

1 二分法

定理1（介值定理）设f (x)在[a,b]上连续，且f(a) f (b)＜0，则至少存在一个点ξ∈(a,b)使得f (ξ)=0，即ξ是f (x)=0的根。

为了便于分析，设f (x)在[a,b]上是单调的，则f(x)=0在[a,b]内只有一个实根ξ。

1.1 基本思想

二分法是一种通用的数值近似计算方法，它的基本思想是判断区间中间值的函数值f ((a+b)/2)的正负号，逐步对半缩小有根区间，直到区间缩小到允许误差范围之内，然后取区间的中点为ξ的近似值。

1.2 具体方法

不妨设f (a)＜0, f (b)＞0；记a1=a，b1=b，区间[a,b]的中点 ξ1=(a+b)/2，再计算函数值 f (ξ1)。如果 f (ξ1)=0，则表示待求的根为 ξ1，否则判断 f (ξ1) f (a)＜0 还是f (ξ1) f (b)＜0。

若 f (ξ1) f (a)＜0，则记 a2=a，b2=ξ1，则求根区间变为 [a,ξ1]；若 f (ξ1) f (b)＜0，则记 a2=ξ1，b2=b，则求根区间变为[ξ1,b]。这样区间[a2,b2]是方程新的有根区间，它被包含在原有根区间[a,b]之内，且长度仅为原区间的一半。对缩小后的区间[a2,b2]，再计算其中点ξ2=(a+b)/2，判断f (ξ2) f (a2)＜0还是f(ξ2) f (b2)＜0。

如此重复上述计算过程，经过k次这样的二分以后，求得的有根ξk区间[ak,bk]的中点ξk=(ak+bk)/2。区间大小。显然，如果无限二分下去，则

因而定义精度ε，当k足够大时，|ξξk-ak|≤（bk-ak）/2=（b-a）/2k〈ε，则ξk就是方程f (x)=0的一个满足给定精度的近似根。

2 自动驾驶仪设计

阻尼-姿态角控制方法是经典控制理论中经常采用的一种方法。常见的俯仰通道阻尼-姿态角方案控制框图如图1所示。

图1 俯仰通道方案控制框图

2.1 传统自动驾驶仪设计

经典控制理论设计的自动驾驶仪是将系统简化为单输入单输出结构，用传递函数描述系统特性，通过根轨迹法、时域分析法、频域分析法来设计系统。这种方法能够直观地了解所选特征点的时域及频域特性，因此在工程实践中，它是战术导弹自动驾驶仪设计的主要方法。但是这种方法需要花费大量的时间和精力调试，设计过程繁琐，尤其当气动模型发生变化时，自动驾驶仪需要重新设计，所以找到一种快速的参数设计方法很有必要。

2.2 变结构控制方法

变结构控制是一种新兴的控制系统设计方法，其非线性表现为控制的不连续性。从理论上说，由于滑动模态可以按需要设计，滑模控制系统的鲁棒性能比一般系统好。然而滑模控制中切换函数在不同滑动模态的切换会引起系统的抖振现象，为了克服滑模控制的抖振问题，国内外学者进行了许多不同的探讨，其中比较有代表性的是准滑动模态法、趋近律法及滤波法等。

2.2.1 基于变结构控制系统设计

以滚转通道为例，设滚转通道的状态方程为：

滚转通道姿态控制的目的是使滚转角趋向稳定，因此定义误差变量e = γ，定义滑动模态s为：

对s微分，得到：

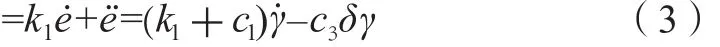
定义趋近律为：

则控制律为：

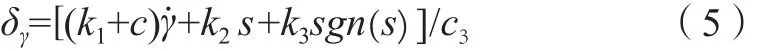
2.2.2 频域特性分析

将变结构控制的非线性特性进行简化，可实现线性控制。以滚转通道为例，令k3＝0则控制律可以简化为:

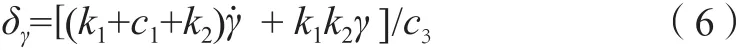
因此，变结构控制在这种特定的情况下等效为1个PD控制器。

选取k1＝10，k2＝10得到10s时刻频域响应情况，如图2所示。

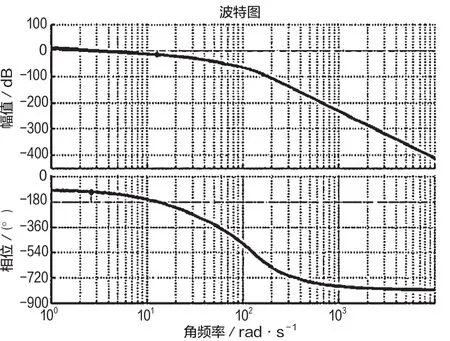
图2 10s时刻频域响应情况

2.2.3 总结分析

k1、k2经过多次调试，滚动通道的幅值裕度在16.1dB左右，相位裕度在75.5°左右。变结构控制存在的不足为：（1）滚动通道的响应效果与k1、k2的选取有很大关系，当k1、k2较小时，滚动通道的幅值裕度较大，响应时间较慢；（2）对系统模型的要求较高，当模型阶次大于二阶时，需要采用降阶方法，会对模型的精确性产生影响。

2.3 基于二分法自动驾驶仪设计

与变结构控制方法相同，基于二分法的自动驾驶仪同样设置成一个PD控制器。以阻尼回路为例，阻尼回路的开环传递函数与阻尼回路参数相关，通过这个传递函数可以得到阻尼回路的幅值裕度、相位裕度、调节时间等频域及时域指标。

2.3.1 二分法逼近参数

将频域指标中的幅值裕度作为性能指标函数F，那么F就能写成与阻尼回路参数K 相关的函数:F=f(K)。经典控制理论设计中，对幅值裕度和相位裕度都有相应的指标要求,如要求幅值裕度不小于16dB。通过二分法可以迅速找到相应的增益Km，使得特征点的幅值裕度为16dB。

二分法要求目标函数呈现单调变化。对于静稳定系统，当增益K ＞0时，系统稳定。随着增益K的增大，系统的幅值裕度减小，因此幅值裕度函数f (K)是一个单调递减函数。但是当增益K继续增大时，系统有可能出现振荡及失稳现象，因此，应用二分法时需要选择合适的边界范围。

选取10s特征点进行频域设计，找到幅值裕度分别为3dB和50dB的增益K2、K3。将[K2,K3]作为边界范围，采用二分法逼近得到幅值裕度为16dB的增益Km。

2.3.2 参数优化

二分法逼近得到的增益Km满足了控制系统对幅值裕度的要求，但是相位裕度、截止频率、超调量、调节时间等指标未必能满足要求。因为幅值裕度函数是单调递减函数，增益K在(0,Km]范围内都能满足幅值裕度要求。

取精度D=100，将增益Km分成100份，Ki= i/100×Km，i =1，2，…，100。

分别计算相应增益的相位裕度、超调量、调节时间等，剔除相位裕度及超调量不满足要求的情况，选出其中调节时间最优的增益。

10s时刻频域响应情况如图3所示。

2.3.3 数学仿真分析

为了验证基于二分法的自动驾驶仪设计的有效性，将设计的参数代入数学仿真进行验证，滚动通道初始加入姿态角和姿态角速度偏差，全程加入风干扰及结构干扰，仿真结果如图4所示。

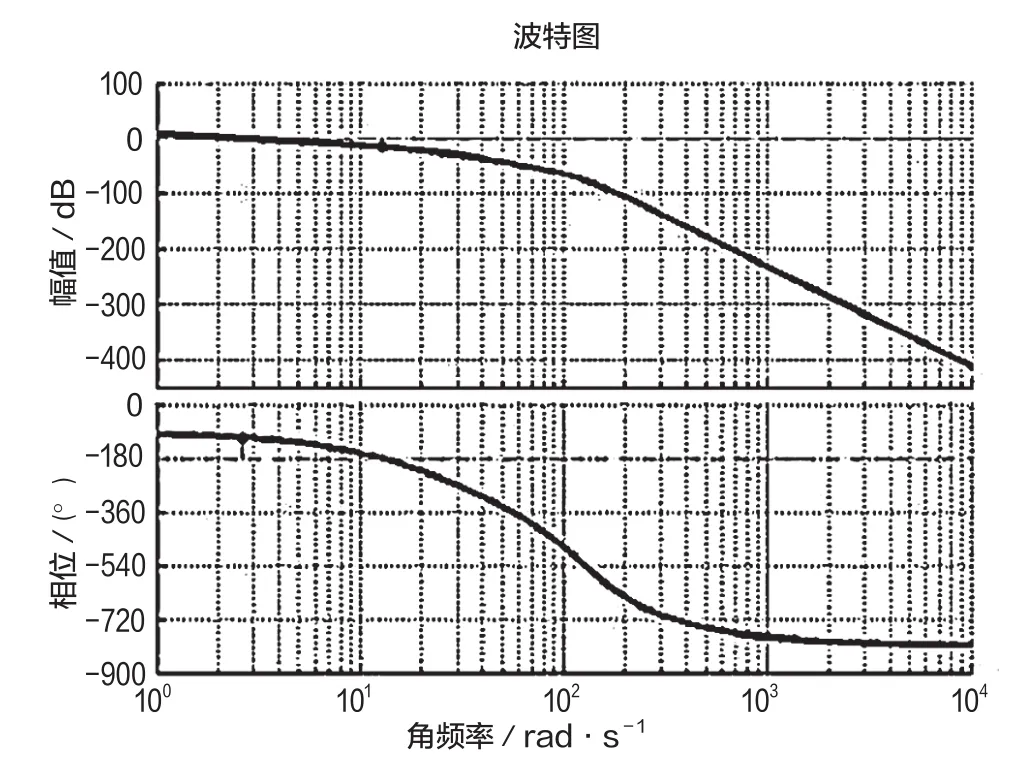
图3 10s时刻频域响应情况

图4 滚动姿态角偏差

分析图4可以看出，滚动通道在5s左右将初始姿态角偏差控制到零附近，由于干扰的存在，滚动姿态角在后续也存在一定程度的变化，这说明设计的自动驾驶仪具有较好的鲁棒性。

2.3.4 总结分析

通过二分法逼近得到增益Km，使得滚动通道的幅值裕度为16dB，对得到的参数进行优化，得到的幅值裕度在16dB左右，相位裕度在70.1°左右。最终的幅值裕度与二分法逼近得到的幅值裕度基本相同，这是因为二分法逼近得到的增益满足相位裕度、截止频率、超调量等指标要求，调节时间是最快的。

通过数学仿真分析结果可以看出，二分法逼近设计得到的自动驾驶仪能够让控制系统稳定，具有良好的鲁棒性。其优点在于：（1）可以根据不同的频域、时域需求，设计不同的增益，使人为调参转换为计算机运算，极大地降低了系统设计的工作量；（2）当系统模型阶次较高时，二分法不会受到影响。

3 结束语

传统的自动驾驶仪控制系统设计需要花费大量的时间和精力，本文提出的基于二分法的自动驾驶仪参数优化设计方法，将人为调参转换为计算机运算，极大地提高了系统设计的工作效率。针对二分法的参数进行优化，能够保证控制系统相应的频域和时域指标满足约束要求。数学仿真结果证明了设计得到的自动驾驶仪的有效性。