三种环境下月壤削坡试验离散元分析

， ， ， ,

(1.上海理工大学 环境与建筑学院 上海 200093； 2.同济大学 岩土及地下工程教育部重点实验室 上海 200092； 3.同济大学 土木工程防灾国家重点实验室 上海 200092)

0 引言

月球作为人类探索太空的第一站，历来受到各国的重视.一方面是因其有丰富的矿物资源、稀土元素及稀有气体，尤其稀有气体3He是一种清洁、安全廉价的核聚变材料，月壤中约含有100～500万吨，以人类目前资源消耗的速度，这些足够使用近万年[1-2]；另一方面，对月球的高真空、高温差、低重力场等特殊环境的研究对太空工程有重大意义.

已有研究表明月壤和地壤存在较大差异，呈“一高两低”的特点：1) 较高的内摩擦角.月壤的形成主要是月岩受到陨石的撞击，宇宙射线的持续轰击以及大幅度的昼夜温差引起热胀冷缩导致最终月岩破碎[3]，因此月壤表面凹凸不平，有很强的啮合作用，进而内摩擦角较高.文献[4]采用离散单元法模拟了月壤的三轴试验，发现采用常规的颗粒接触模型模拟得到内摩擦角的范围为29°～37°，难以匹配真实月壤内摩擦角43°～51°. 2) 较低的微距力.月壤的土性类似砂土，传统土力学认为其不应具有黏聚力，但有学者认为由于月球表面缺少大气层，表面接近真空状态，月壤颗粒表面吸附气体分子层厚度远小于地面土壤颗粒，在地面环境下无需考虑的微距力在月面环境下应该给予考虑[5-6].通过考虑微距力能够使月壤具有一定的黏聚力，能够更加接近真实月壤力学特性[7-8].文献[9]针对月壤展开了不同真空度条件下的三轴试验，结果表明摩擦角与真空度关系不大，但黏聚力与真空度存在一定的联系. 3) 较低的应力水平. 在地球上，岩土工程中的自重应力通常起支配作用，土的力学特性随应力水平而变化，月面环境下重力场大约为地面环境下的1/6[3]，月壤地基初始应力也较小.土体形成坡体允许的最大坡角和休止角直接相关，而休止角的大小是否会受到重力场的影响至今尚无定论.文献[10]认为休止角随着重力减小而增大，而文献[11]认为休止角不受重力大小的影响.相关的研究表明地月环境差异对静力触探试验[12]、推剪开挖[13]和地基承载力试验[14]都有一定的影响，然而，其对月壤边坡工程是否存在影响却少有研究，直接相关的文献较少，而间接相关文献主要围绕现场试验、室内试验和数值模拟展开.现场试验：根据Apollo15探测器对月球表面雨海东部边缘现场影像数据分析，部分地区发现了滑坡运动的证据[1].根据嫦娥三号返回数据，分析发现月球表面存在不少的高陡边坡，坡度一般大于30°，月海区可达48.9°，月陆区甚至可达55.7°[15].通过现场的沟槽试验也表明了月壤具有较高的自稳能力[11].室内试验：文献[16]采用月壤模拟物研究了不同基岩倾角下的月壤滑坡试验，研究发现了月壤滑坡过程中出现裂隙面和光滑面，然而这种模拟月壤只是在级配及材料相似，而没能考虑低重力场及表面微距力.数值模拟方面：文献[17]认为真实月壤的化学成分可能产生了附加黏聚力，故在微观模型中加入黏聚力，虽然数值模拟滑塌试验与真实月壤符合较好，但附加黏聚力没有严密理论的支持.文献[18]基于离散单元法采用了一种考虑范德华力和抗转动作用的月壤模型，并分析了地面环境和月面环境下剪切带的形成机理和力学特性，发现模拟月壤在月面环境下会比地面环境具有更高的强度，更易形成应变局部化.文献[19]通过离散单元法分别考虑了月面环境、不考虑范德华力的月面环境和地面环境，对比分析了重力场和范德华力对水平开挖试验中推剪阻力和能量消耗的影响.

多尺度研究方法[20]越来越受到人们的重视，而离散单元法能够很好地模拟颗粒材料大变形问题，深入土体的微观领域去研究其本质规律，故本文采用离散单元法模拟月壤滑坡试验.借助PFC2D软件，通过植入二维月壤接触模型，模拟3种不同环境下(地面环境、不考虑范德华力月面环境和月面环境)的月壤坡体滑坡试验，观察分析滑动过程的变形特性，对比分析了重力场和范德华力对滑坡过程中流滑距离、最终倾角及坡后沉降的影响，为将基于地面环境设计方法推广到月面环境提供了理论依据及设计参考.

1 月壤微观模型介绍

本文所采用的微观模型是本团队最近提出来的，主要考虑月壤颗粒间的抗转动作用及范德华力，该模型充分考虑月壤的颗粒形态和月球表面的真空环境，比之前的模型更为完善，模型的有效性可以参考文献[7-8].通过对真实月壤的颗粒形状加以观察，发现月壤的颗粒形状以长条状、次棱角状和棱角状的较为普遍，如图1中黑色颗粒所示，颗粒之间的凹凸不平，具有很强啮合作用，颗粒之间有着很强的抗扭转作用.在传统的离散元颗粒接触模型中，颗粒之间都是点点接触，所以只考虑法向和切向的力学相应，而在本模型中考虑到月壤的真实轮廓及内摩擦角偏大的现象，在常规模型中增加了转动向的接触模型.

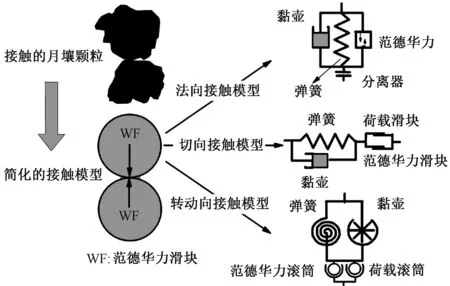
图1 月壤微观接触模型[7-8]Fig.1 Micro contact model of lunar soil[7-8]

月球表面接近真空的状态使得月壤颗粒表面吸附的气体分子层厚度远小于地面土壤颗粒，此时，范德华力的作用不可忽略.范德华力的计算公式可以简化为

.

(1)

式中：D为颗粒所吸附的分子层厚度，与月面环境的气压和气体分子种类相关，根据Adamson的吸附势理论计算[21]；A为Hamaker系数，取值4.3×10-20J[6]；β为表征颗粒粗糙程度的抗转动系数；r为两颗粒之间的等效半径，r=2r1r2/(r1+r2)，其中r1、r2分别为两接触颗粒的半径.

2 月壤边坡模型建立

在采用离散单元法模拟月壤滑坡试验过程中，若直接采用与真实月壤颗粒相同的级配，就会导致颗粒粒径跨度过大，所需颗粒数目非常多，考虑到计算机能力及计算效率，对月壤级配做合理简化[7-8].根据Mitchell[22]等测得真实月壤的黏聚力值范围为0.1～1.0 kPa，内摩擦角范围为30°～50°，通过模拟双轴试验进行对月壤宏观参数标定，微观参数与文献[7-8]一致，得黏聚力c=0.2 kPa，内摩擦角约为φ=42.6°，处于真实月壤的范围之内.

图2为采用离散单元法的数值模拟过程中边坡形成的示意图.本次模拟中坡体的形成主要经历3个阶段：首先采用文献[23]提出分层欠压法生成相对密实均匀的地基，两侧墙及底墙为无摩擦的刚性墙，顶部为自由边界，地基宽度为5 m，初始高度为2.5 m，颗粒总数为1.5×105.其次，试样需要在1/6g重力场下完成固结平衡，来模拟真实月面环境下地应力水平，固结完成后地基中水平应力及孔隙比分布如图3所示，可知固结平衡后的地基初始应力数值解和理论解基本一致，且孔隙比分布均匀.最后，需要对地基进行切坡处理，此处选取初始坡角为60°，略大于月陆地区的极值55.7°，在其重力场下自由滑塌过程，这有助于模拟可能出现最危险的滑坡灾害.在具有月壤特性的坡体形成后，坡体需要分别在地面环境(1g)、不考虑范德华力月面环境或称简化月面环境(1/6g)及月面环境(1/6g+范德华力)下完成滑坡试验，达到系统的第2次平衡，同时记录滑坡过程的微观信息.为了保证月壤材料性质不变，同时保证破坏过程只有单一重力场，坡体破坏的触发方法既不是强度折减法也不是重力增加法，仅仅只是高坡角下自重滑塌.

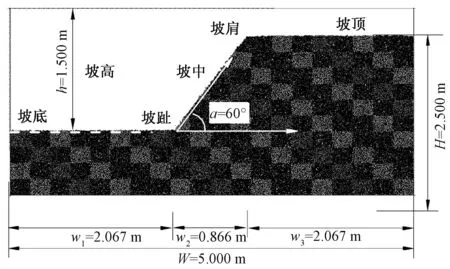
图2 数值模拟中边坡模型Fig.2 The slope model in DEM analyses

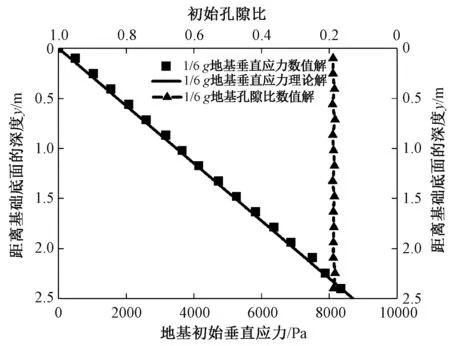
图3 1/6重力场下地基初始应力水平及孔隙比分布Fig.3 Distribution of initial stress and void ratio in the ground under 1/6 g

3 模拟结果分析

3.1 变形图

图4给出了地面环境和月面环境下滑坡过程变形示意图.无论地面环境还是月面环境都经历3个阶段：启滑阶段、滑动阶段及稳定阶段.启滑阶段，地面环境与月面环境下滑坡临空面出现轻微的滑动，几乎看不出明显的差异.滑动阶段，通过网格变形能够看出大致的滑动面，地面环境的滑坡体区域比月面环境下滑坡体区域大，这是因为地面环境的重力场为1g，远大于月面环境下的重力场1/6g，较高的重力场使得颗粒具有的势能越大，下滑过程做功也越大，影响的范围也越大.通过将滑坡体表面局部放大，发现月面环境下滑坡体的滑坡表面较为粗糙，出现微小的张拉裂隙.这主要是因为月面环境下颗粒之间因范德华力作用，能够相互吸引，抱成团簇顺坡滚动，带走部分黏附颗粒，使得其临空滑动面坑坑洼洼，表面粗糙，而地面环境下模拟月壤颗粒之间摩擦力很小，呈现散粒体的滑动，表面容易形成光滑面.更进一步，月面环境下滑坡体倾斜角度比地面环境下要更为陡峭，这可以归结于低重力场和范德华力之间共同作用引起的.重力场越小，越不易打破原来的土体平衡，范德华力的存在使得月壤之间含有微弱的黏聚力，使得坡体更加趋于稳定.相比滑动阶段而言，稳定阶段的最大特点是滑坡的区域开始包括了坡底水平线以下的土体，滑坡体从原来的两端相当的“梭子状”变为下宽上窄的“铲子状”.此时，通过滑坡舌的局部放大图，可以看出地面环境下的滑坡体容易出现坡趾挤压现象，而月面环境下坡趾则几乎没有挤压，网格主要呈现水平拉长现象，坡底水平线以下的土体扰动较小.需特别指出，限于篇幅此处未给出简化月面环境下滑坡过程，但其主要两个特征均在地面和月面环境中出现：简化月面环境与月面环境下滑坡最终轮廓线相似，简化月面环境与地面环境下坡体表面光滑度相似.重力场会主要决定滑坡最终的倾角及滑坡体的影响范围，而范德华力则主要影响坡体表面的光滑度.

通过一定的算法提取滑坡前后的变形轮廓线及工程指标，如最终倾角、流滑距离及坡后沉降，如图5所示.通过对滑坡前后形态对比分析，发现滑坡过程也可以看成土体围绕坡面中点呈现中心对称转移颗粒的过程.相比月面环境，地面环境下滑坡的转移区域大，流滑距离也大，最终倾角小，坡后沉降大，这表明同样的边坡在地面环境更为危险.相比月面环境，简化的月面环境对最终倾角、流滑距离和坡后沉降有轻微的影响，但这种影响都是偏于安全，设计时可以近似忽略不计.

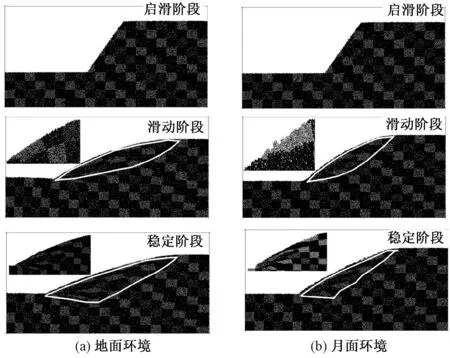
图4 滑坡过程形态对比分析Fig.4 The comparison on landslide configurations

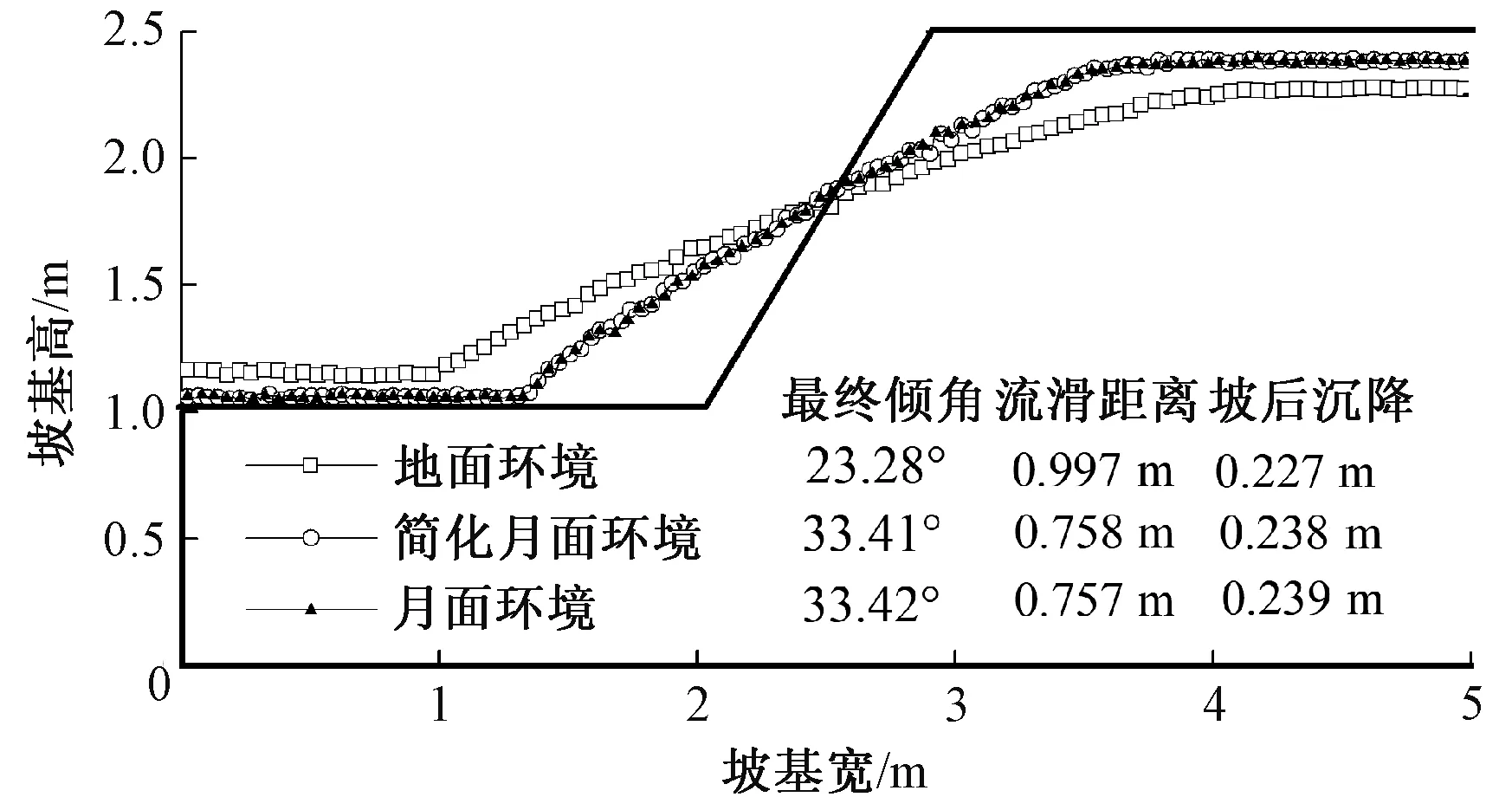
图5 滑坡前后形态对比分析Fig.5 The initial and final configurations of slopes

3.2 速度场

为了更好利用速度场描述滑坡过程，将所有的颗粒运动过程简化为速度场矢量箭头，并将其划分成7个等级，分别用7种灰度表示，如图6所示.颗粒的速度矢量箭头方向是根据颗粒在1个时间段内两个位置之间的连线形成，速度矢量箭头的长短是取决于速度的大小，同时将某一时刻的所有的速度大小对该时刻的最大速度作归一化处理.

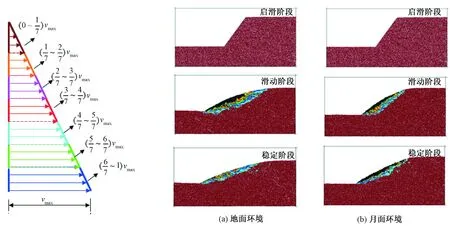
图6 滑坡过程速度场对比分析Fig.6 Comparative analysis on velocity vectors in the DEM landslide

图6给出了地面环境和月面环境下滑坡过程速度场示意图.启滑阶段，滑坡表面并没有明显的差别，在边坡的临空面会出现特大速度，其余部分均分布在小速度范围之内，表现出颗粒运动过程中速度梯度差极大.滑动阶段，地面环境和月面环境下的高速度场都主要集中在滑动面上，且地面环境下高速度场区域比月面环境下的区域要大许多，这与之前网格变形图相一致.稳定阶段，高速度场区域逐渐减小，但月面环境下速度出现两极分化较为严重，而地面环境下速度梯度较为缓和，两者都从条状逐渐变为线性状，表明整体速度逐渐稳定.

3.3 最大速度和最大动能分析

滑坡的速度直接决定滑坡时长，亦是人类对抗滑坡灾害反应的时间，如快速滑坡比缓慢滑坡更易造成对生命财产的破坏，因此研究滑坡过程的速度变化规律具有重要的工程意义.图7(a)给出了3种环境下最大速度vmax随时间变化的规律.随着时间的增长，最大速度逐渐增长并且在0.8 s内相继完成峰值，随着时间的增长最大速度逐渐接近零.滑坡全过程中，地面环境下的最大速度都大于简化月面环境和月面环境.值得注意的是，简化月面环境和月面环境的最大速度变化规律曲线在1.6～2.0 s时会出现第2次小峰值的现象，这可能是因为低重力场下原本渐趋稳定的颗粒，受到上方颗粒惯性推动和吸引抱团成簇，最终不堪受重力作用驱使，形成小规模成团滑动，导致加快速度.此时，若将最大速度与其对应单颗粒的质量做动能分析，发现这种二次波峰现象得到有效的减小，如图7(b)所示，这也从另一个角度验证了颗粒微聚力能帮助土颗粒抱团成簇运动的假说.

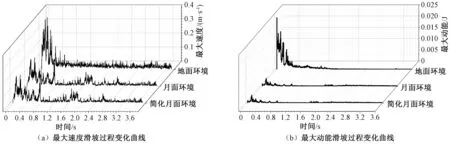
图7 滑坡过程中颗粒的最大速度和最大动能Fig.7 The maximum velocities and the total kinetic energy of grains in the DEM landslide

3.4 滑坡过程中功能转化分析

滑坡过程总是伴随物质的流动和能量的转换.为了更好地理解环境差异引起的滑坡机理，本文对滑坡过程中能量的来源及去向做了较为深入的剖析.针对月面环境与地面环境的差异主要是在重力场和范德华力，而重力场做功是本次滑坡过程中唯一的能量来源.

重力做功为

Δyk.

(2)

颗粒的总动能为

(3)

颗粒的摩擦总功为

Ef=FsΔslip=(μWg)Δslip.

(4)

颗粒的应变能为

(5)

其中：Δyk为累计下落距离；Δslip颗粒摩擦滑移位移；Fn,Fs分别为法向和切向力；kn,ks分别为颗粒法向刚度和切向刚度.滑坡前后的能量主要有：滑坡开始前能量主要以重力势能存储；公式(2)中滑坡过程中重力做功Wg使得重力势能逐步转换为颗粒的动能、颗粒之间摩擦消耗的能量、颗粒之间接触所存储的应变能，其计算公式分别对应公式(3)、(4)和(5).需要说明的是，由于本文设置三面墙体均为无摩擦刚性墙，所以此处不考虑墙与颗粒摩擦所消耗的能量.

图8(a)给出了3种环境下模拟月壤物在滑坡过程中重力所做的功随时间变化的规律.滑坡过程中，重力在地面环境做功远远高于在月面环境下所做的功，而且地面环境做功略高于月面环境做功的6倍，这表明月面环境下颗粒整体下移动的趋势受到约束，而是否考虑月面环境中的范德华力，对重力做功影响较小.图8(b)给出了3种环境下月壤在滑坡过程中颗粒总动能随时间的变化规律.3种环境中动能都经历了1个明显峰值阶段，这对应滑坡过程的滑动阶段，此时重力做功迅速增大，对应系统颗粒动能陡增现象；随后总动能都逐渐减小，这对应滑坡过程的从高速滑动向稳定阶段发展，此时所有的颗粒速度都在不断减小；随着滑坡演化，颗粒之间动能逐渐平稳最终趋近于零，表明坡体最终得到稳定.地面环境下的动能也远高于月面环境，这主要是因为高重力场做功较大，转换为动能也较多，而简化月面环境与月面环境之间差异较小，范德华力对颗粒总动能的影响也较小.图8(c)给出了3种环境下模拟月壤物在滑坡过程中颗粒之间摩擦消耗的能量随着时间变化的规律.颗粒之间摩擦耗能与重力做功极为相似，这由公式(4)计算也可以体现，因为摩擦力做功与应力水平直接相关，月面环境下重力做功增速较快，而月面环境的增速较慢.稳定阶段，摩擦累计做功得到稳定，基本保持不变.由此可见，就摩擦耗能而言，比起范德华力，重力场仍起主导作用.图8(d)给出了3种环境下月壤在滑坡过程中颗粒受到挤压存储于接触之间的应变能随时间变化的规律.

与重力做功、摩擦做功不同，颗粒的应变能变化规律较为复杂，应变能不是简单的累计，而会出现上下波动，这也可以理解，因为位置较高的颗粒，原本受到挤压的颗粒随着滑坡的进一步发展，会出现应力释放伴随原有的应变解除现象，这样部分能量就会转化为颗粒动能，当颗粒到达坡地时，又会对坡地的颗粒产生一定压力，使得坡底的颗粒应变能升高.而一旦滑坡达到稳定时，颗粒的应变总能就达到了稳定值，不再波动.通过两两对比，重力场仍是决定颗粒应变能的主要因素.功能转化的过程是一个相互影响的复杂的渐变过程，期间各因素之间如何相互影响暂时难于研究.值得注意的是，简化月面环境和月面环境下功能转化仍存在一定的差异，这种差异主要是范德华力对颗粒之间的相互影响也会消耗部分的功.

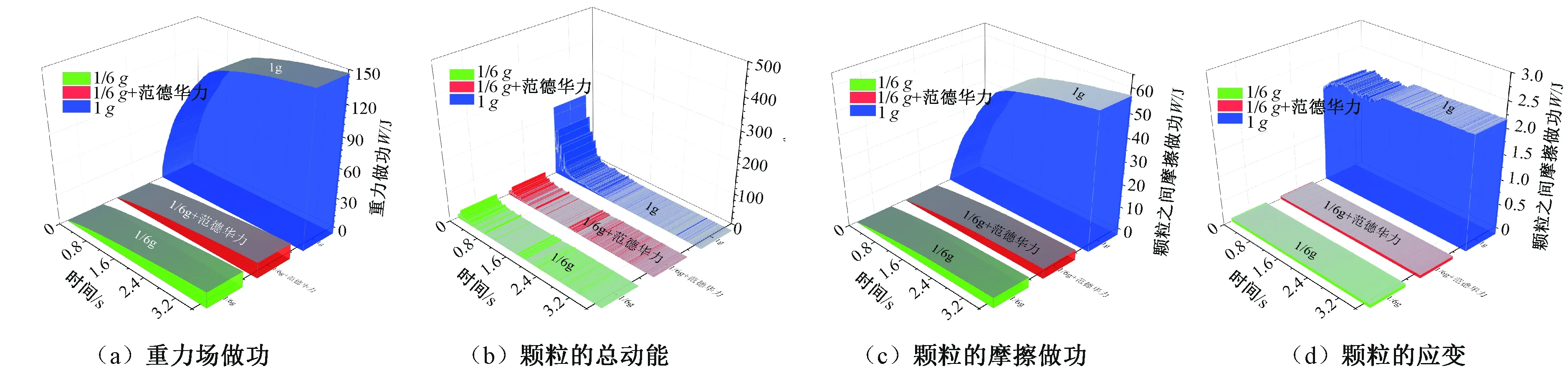
图8 滑坡过程中的能量分析Fig.8 Energy analysis in the landslide

4 结论

本文通过引入能够考虑范德华力及抗转动作用的月壤微观接触模型，采用离散单元法模拟了月壤切坡试验，从3种环境(地面环境、简化月面环境及月面环境)下对比分析了重力场和范德华力对滑坡机理的影响，主要结论如下.

1) 通过地面环境和简化月面环境对比分析，得到重力场对滑坡的形态、最终倾角、流滑距离及坡后沉降都有显著的影响；同时通过简化月面环境与月面环境对比分析，得到范德华力对滑坡过程中滑坡的形态、最终倾角、流滑距离及坡后沉降的影响有限，考虑范德华力后，坡体的危害指标整体偏安全.

2) 通过速度场的分析，表明月面环境下滑动体影响范围比地面环境范围较小.通过对比分析最大速度和最大动能的关系得到滑坡过程中验证了范德华力对滑坡表面颗粒有一定约束作用.

3) 通过分析滑坡过程中的功能转化，得到滑坡过程中重力场在滑坡做功中起决定性的作用，而范德华力对做功影响有限，一定程度上可以忽略其影响.