基于样本双重选择的马尔科夫链光伏功率预测

郭 婕，厉 虹，王丽婕

(北京信息科技大学 自动化学院，北京 100192)

0 引言

光伏发电行业发展迅猛，但其具有的随机性和波动性使得其并入电网时对电网的安全稳定运行造成巨大的冲击。为了对电网进行合理调度，提高电力系统运行的安全稳定性，有必要对一段时间内的光伏发电功率进行预测[1]。

国内外学者对光伏功率预测进行了广泛的研究。常用的预测方法有神经网络法、马尔科夫链法、支持向量机法等[2-4]。上述方法中，神经网络具有快速局部搜索能力，可迅速寻找到优化解，在光伏预测中获得了较为普遍的应用。但神经网络寻优容易陷入局部最小，无法得到问题的最优解，而且迭代收敛速度慢[5]；支持向量机法运算简单，收敛速度快，具有较强的逼近能力和泛化能力，但参数互相影响，难以确定[6]；马尔科夫链预测法是适用于随机过程的一种预测方法，这种随机过程的特征与光伏发电功率的随机性和波动性相符，由于其具有的科学有效性，国内外学者正在将马尔科夫链法应用到光伏功率预测中。文献[7-8]分别采用传统神经网络和相似日神经网络建立预测模型，通过马尔科夫链对预测结果进行修正，结果表明选择相似日建立预测模型的预测精度更高；文献[9]选取预测日前30天的数据，对每个采样时刻的功率利用马尔科夫链预测，由于没有考虑对历史数据进行选择，存在较大的预测误差。马尔科夫链预测是一种计算概率的预测方法，它的预测精度会受到选择样本的影响。

针对这一问题,本文采用加权灰色关联度对历史数据进行初次选择，再根据格拉布斯(Grubbs)准则进行二次选择，然后通过选择的相似日建立马尔科夫链(Markov chain)预测模型进行光伏功率预测。

1 相似日选择

光伏电站的输出功率与辐照度、温度等气象因素密切相关，气象相似度高的2天光伏输出功率曲线有较好的相似性。因此选择相似日可以更好地对预测日的功率进行预测。

1.1 加权关联度

为了得到关联度,首先计算光伏功率与各气象因素的相关系数：

(1)

归一化后得到各气象因素的影响权重：

(2)

式中：rj为第j个气象因素与光伏功率的相关系数；m为气象因素个数。

设X=[Favg,Tmax,Tavg,Tmin,Yavg,Savg]为气象特征向量，其中Favg为辐照度，Tmax、Tavg、Tmin分别为最高温度、平均温度、最低温度，Yavg为全云量，Savg为风速。选择预测日和历史日的气象特征向量X0和Xi为参考序列和比较序列，计算预测日与历史日的关联度。

第i个历史日的第j个气象特征与预测日的关联系数为

(3)

不同气象因素对光伏发电功率的影响程度不同，合理地选择各气象因素的影响权重能够提高选择相似日的准确度。所以计算完所有特征分量的关联系数后，第i个历史日与预测日的加权关联度为

(4)

γ越大，说明该历史日与预测日的相似度越高。选择相似度较高的历史日作为初步的训练样本集。

1.2 格拉布斯准则

相似日选择的好坏直接关系到预测结果的精度。为了进一步提高模型的预测精度，本文选择Grubbs准则对初次选择的相似日进行二次筛选。Grubbs准则是滤除异常数据常用的一种方法，引进了平均值和方差2个参数，而且不同的数据量具有不同的临界值参数(异常值判定标准)，与固定判断标准相比，Grubbs准则更具有理论上的合理性[10]。

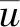
(5)

(6)

然后比较其与临界值大小，剔除异常数据，完成二次筛选。

在光伏功率预测中，预测模型直接决定预测效果，而预测模型的好坏部分取决于训练样本数据。所以找出与预测日相似度高的历史日数据训练预测模型是提高模型预测效果的有效途径。Grubbs准则的作用就是对初次选择的相似日进行异常检查，剔除其中的异常值，增强所选择样本的相似度，再建立预测模型进行预测。

2 预测模型设计

2.1 马尔科夫链

马尔科夫链预测是研究事物状态以及状态转移的一种概率预测方法，对事物的初始状态概率和各状态之间的转移概率进行研究以判断总体变化趋势，预测系统未来的状态[11]。

把相似日同时刻的功率视为一个随机过程{y1,y2…,yt}，确定每个功率所属状态区间s，S={s0,s1,s2…sN}，其中状态si出现的次数总和记为Fi，状态si经过一步转移到状态sj的次数记为Fij，则一步状态转移概率为

(7)

所有状态转移概率的集合形成的矩阵为状态转移概率矩阵：

(8)

根据初始时刻功率所处的状态确定初始状态概率向量：

(9)

式中：P(y0=si)为初始功率属于某状态区间的概率。

状态转移概率矩阵和初始状态概率向量相乘，得到预测时刻功率的状态概率向量：

PY=P×P0

(10)

功率状态的期望向量PEXP取每个状态区间的平均值，通过与预测时刻功率的状态概率向量相乘得到预测时刻的功率值：

Y=PEXP×PY

(11)

马尔科夫链预测的关键是状态转移概率矩阵。选择不同的样本会有不同的转移概率，直接影响到最终的预测结果。为了提高预测精度，本文用灰色关联度和Grubbs准则对历史日进行选择。基于灰色关联度理论，根据各种气象因素从历史日中挑选出与预测日具有较高相似度的历史日样本，利用Grubbs准则对选择的历史日功率数据进行检验，判断是否存在异常数据，完成二次筛选。基于相似日的马尔科夫链功率预测流程如图1所示。

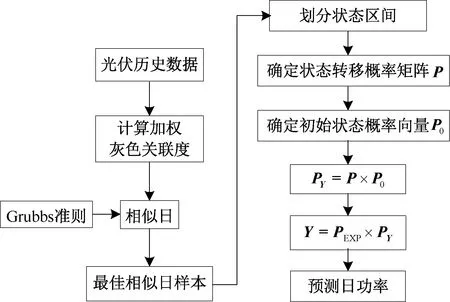
图1 预测流程

2.2 评价指标

采用平均绝对百分比误差和均方根误差对预测模型的预测结果进行评估。

平均绝对百分比误差为

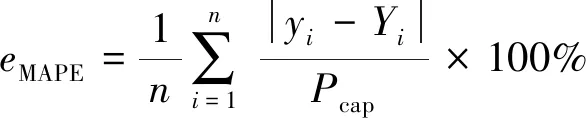
(12)

均方根误差为

(13)

式中：Pcap为光伏电站的功率额定值；yi为实际功率值；Yi为预测功率值。

3 算例分析

选择新疆石城子20 MW光伏发电站的历史气象数据和功率数据进行建模和预测。选择每天7:00—20:00的发电功率，采样时间间隔为15 min，一天共53个功率数据。2—6月份的数据作为历史样本，7月份的数据作为预测对比样本，以晴天、晴转多云、多云转雨3种天气类型为例进行实验。

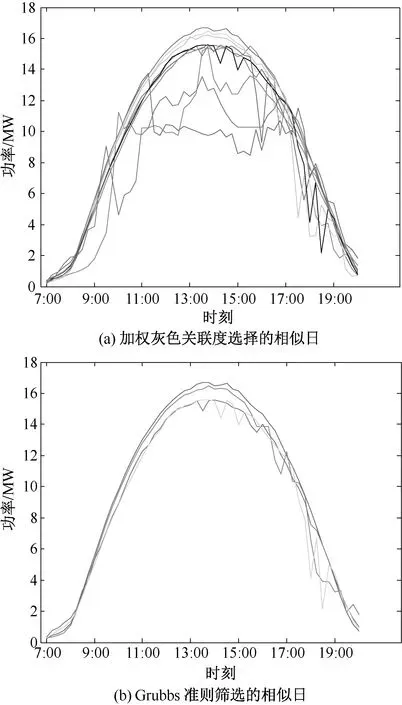
图2 相似日选择结果

首先，根据历史数据样本和式(1)、(2)，计算得到各气象因素对功率的影响权重。通过加权关联度式(3)、(4)计算历史日与预测日的关联度，从大到小进行排序，选择前15天的数据作为初步的相似日样本。然后，对相似日每个采样时刻的功率值计算Grubbs统计系数，通过查表比较，删除存在异常功率值的历史日，完成二次筛选。以晴天为例，2次选择后的相似日如图2所示。可以看出，采用加权关联度选择的相似日中存在相似度差的历史日，经过2次筛选后可以剔除异常历史日，得到功率曲线变化趋势相似的历史日，作为相似日样本。

将相似日的功率划分成N个状态区间，每个区间长度l=(Pmax-Pmin)/N，确定各个功率所属的状态区间，然后进行马尔科夫链预测。选择不同的状态区间数n进行预测，得到模型的预测误差如图3所示。

图3 状态空间数n对预测模型的影响

从图3可以看出，选择不同的状态区间数N，模型有不同的预测误差。当N取3时，光伏发电功率的预测误差最小，随着N的增大，预测误差明显增大，所以本文选择状态区间数N=3。

确定了状态区间数后，建立马尔科夫链预测模型，得到3种天气类型的预测结果如图4所示。图中给出了预测值与实际值曲线，为了对比预测效果，也给出了未进行Grubbs二次筛选和未选择相似日的预测结果。

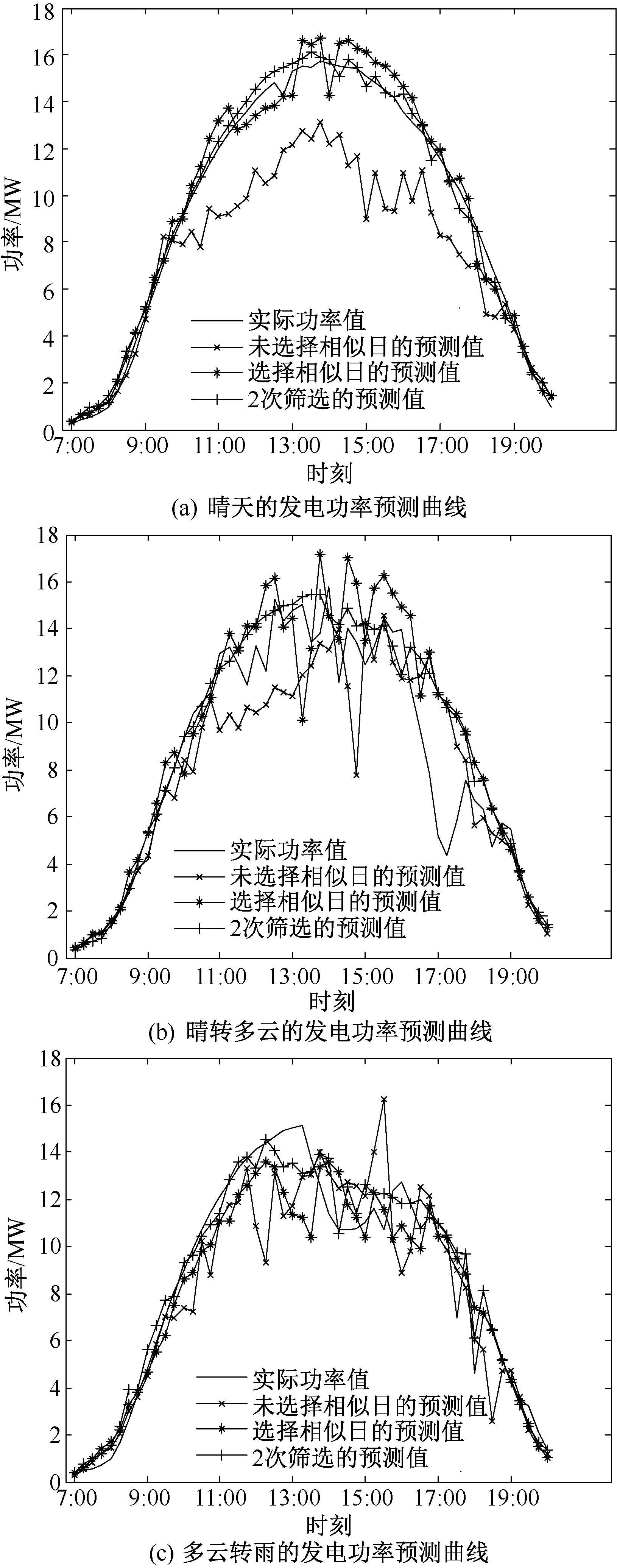
图4 不同天气类型的预测结果

观察图4可知，未选择相似日直接进行预测，整体的预测误差偏大；采用加权关联度选择相似日之后，预测精度有所提高，只是在个别时刻点存在误差。以晴天为例，大体趋势是正确的，只是在第19、25、29点附近有波动，这是因为马尔科夫链是依据概率来进行预测的，如果某个时刻的功率序列中存在有偏差的功率值，就有可能对预测结果产生影响；经过二次筛选，剔除异常功率值，预测结果对上述存在波动的时刻点的功率进行了修正，预测结果更加接近实际功率值。

根据式(12)、(13)计算平均绝对百分比误差和均方根误差对预测结果进行评估，如表1所示。预测方法A代表没有选择相似日，B代表加权关联度选择相似日，C代表经过二次筛选。图5为晴天每时刻的绝对百分比误差。

表1 预测评价指标 %

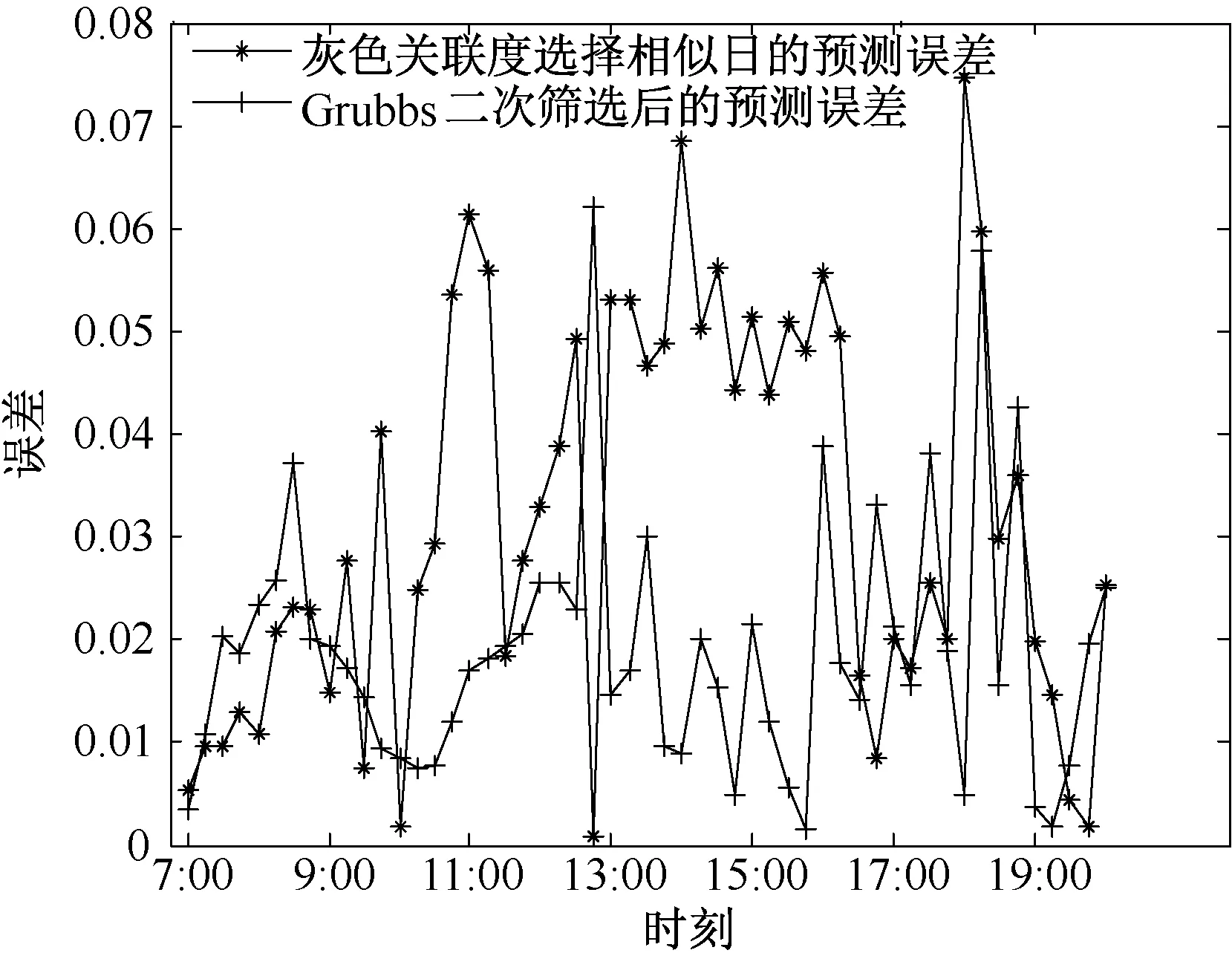
图5 预测误差曲线

从表1和图5可以看出：

1)不同天气类型下，基于相似日的马尔科夫链预测模型的预测误差均低于马尔科夫链直接预测的误差。晴天的预测效果最好，平均绝对百分比误差和均方根误差分别降低了约7%和10%。

2)对相似日的功率数据采用Grubbs准则进行2次筛选后，预测结果进一步提高。晴天的预测误差基本控制在4%以内。多云转雨的平均绝对百分比误差和均方根误差分别降低了约2%和2.5%。

3)选择相似日再进行预测，提高了预测精度，并且符合《光伏发电功率预测系统功能规范》中的预测精度要求。

4 结束语

为了提高光伏功率的预测精度，本文通过加权灰色关联度和Grubbs准则完成2次筛选，并基于相似日建立了马尔科夫链预测模型。通过与未选择相似日的预测模型相比，双重筛选后的预测模型的平均绝对百分比误差在3种天气类型下分别降低了8.78%、2.34%、3.79%。说明加权关联度和Grubbs准则可以有效提取相似日，降低预测模型的预测误差。在后续的工作中，尝试用不同的方法进一步对历史样本进行数据挖掘，找到更接近预测日的历史日样本，提高预测精度。