吉布斯佯谬
金玉霞 李鹤龄
(宁夏大学物理与电子电气工程学院,宁夏 银川 750021)
对于理想气体在混合前后熵的变化,吉布斯曾经提出了著名的“吉布斯佯谬”。现在,在一般的热力学、统计物理学教材和期刊中都可以见到有关论述[1-10]。但是,在这些教材和期刊中对吉布斯佯谬表述仍然不一[1-10]。在现今国内的绝大部分《热力学与统计物理学》教材中,关于吉布斯佯谬的解释基本一致,通常认为[1-3]:吉布斯佯谬是由建立在经典力学基础上的统计物理不能解释的,在量子理论中考虑了粒子的全同性,吉布斯佯谬将得到合理的解释。但是,当考虑了量子粒子全同性之后,会产生更多的佯谬[4,11]。由此可见,引起佯谬的本质原因不是没有考虑量子粒子的全同性。本文针对在考虑了量子粒子的全同性之后所出现的佯谬,通过量子理想气体混合后组元粒子数密度的突变来解释佯谬。
1 吉布斯佯谬
吉布斯佯谬的引出来自于热力学,在混合理想气体中如果用xr表示混合气体第r组元的分压pr与总压强p之比,则
xr=pr/p=nr/∑nr=nr/n
(1)
式(1)中nr为第r组元的摩尔数,n是总摩尔数。xr也称为第r组元的摩尔分数,混合理想气体的熵可表示为[1]
(2)
式中,cPr为化学纯的r组元的定压摩尔热容;s0r为纯r组元的摩尔熵常数。其中
C=-R∑rnrlnxr
(3)
因为xr<1,所以C>0。式(2)的第一部分为各组元单独存在时,其T、p分别和混合气体的T、p相等时的熵之和。式(2)说明混合前各组元的总熵和混合气体的熵不等,式(3)正是混合后的熵增。为简单,现考虑两种气体混合过程。设初态A为两种纯理想气体,它们有相同的T和p,总熵SA为两部分之和,即
(4)
末态B是混合以后,应该用理想气体的公式(2),即
(5)
熵的改变为
(6)
若令
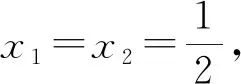
于是,混合后的熵增为
ΔS=C=nRln2>0
(7)
系统与外界隔绝,是孤立系;其内部发生了两种气体的扩散,这是一个不可逆过程,计算得到熵增加。不论这两种气体的性质如何,只要它们有所不同,这个结果都是正确的。但是如果两种气体是同一种气体,根据熵的广延性质,混合后的熵等于混合前两部分熵之和,即C=0。这个结果与式(7)矛盾,也就是由性质任意接近的两种气体过渡到同种气体,熵增突变为零,但是按照式(2)、式(3)计算熵依旧增加,这种表面上出现的矛盾就称为吉布斯佯谬。
2 吉布斯佯谬的解释
对于吉布斯佯谬传统的解决办法是考虑粒子的全同性,然后在统计物理的框架内解释。文献[3]较详细给出计算与分析过程。
当考虑到粒子的全同性前后,单原子分子经典理想气体的熵分别为[3]

按上述混合过程,由式(8)的熵,混合后熵增为式(7),对于同种气体,出现吉布斯佯谬;由式(9)的熵,对于同种气体,混合后熵增ΔS=0,吉布斯佯谬得以解决。
但是,接下来会看到即使考虑了粒子的全同性,在量子理想气体中还是会出现更多的佯谬。下面就对该佯谬做进一步的探讨,由此可以看出引起佯谬的本质原因。
理想玻色子和费米子系统是典型的理想量子气体,在常温下量子理想气体的巨分配函数的对数为[1]
(10)
其中z≡e-α称为逸度,上面的符号(“+”)对应玻色子,下面的符号(“-”)对应费米子。
由巨正则系统熵与内能表达式
计算可得


z=(N/V)(h2/2πmkT)3/2
(15)
将式(15)代入式(13)、式(14),并只取到z的一阶项,得
由巨正则分布可证明,弱简并理想气体的熵、内能等于各组元的分熵、分内能之和。由式(16)、式(17)得混合弱简并理想气体的熵、内能,分别为
对于玻色气体δ=-1;对于费米气体δ=+1;如果令δ=0则成为非简并气体的内能和熵。式(18)、式(19)说明:弱简并理想气体的内能和熵不仅与温度有关,还与粒子数密度和粒子质量有关。
考虑在设有隔板的容器中,放置两种不同的气体分别记为1、2,但其粒子数均为N,体积均为V,粒子质量分别为m1、m2,使这1、2两种气体等温混合。
2.1 简并气体熵的佯谬
混合前两种气体的总熵为
(20)
如果抽取隔板,两种气体通过扩散而混合,混合后的体积为2V,在此过程中保持温度不变,混合后的熵为
(21)
等温混合后熵的变化为
(22)
对于非简并理想气体,δ=0,于是有
ΔS=2Nkln2=2nRln2
(23)
如果当容器两边为同种气体,这时m1=m2=m,抽取隔板熵应该不会变化,但是从式(22)能够得到
ΔS=2Nkln2-5δN2kh3/32V(πmkT)3/2
(24)
出现的这种矛盾就是简并气体的吉布斯佯谬。它比非简并理想气体(单原子分子就是经典理想气体)还多出了式(24)中的右侧第二项。
2.2 简并气体内能佯谬
混合前两种气体的总内能可以写为
(25)
如果抽取隔板,两种气体通过扩散而混合,混合后的体积为2V,在此过程中保持温度不变,混合后气体的内能为
(26)
所以,混合前后内能的变化为
(27)
如果隔板两边放的是同种气体,这时m1=m2=m,抽取隔板前后系统没有发生变化,应有ΔU=0,但是按照式(27)得
ΔU=-3δNh3/32V(πm)3/2(kT)1/2
(28)
出现的这种矛盾称为简并气体的内能佯谬,它是非简并气体所没有的。
量子气体不仅有熵佯谬、内能佯谬,还有焓、自由能、压强等佯谬[4,11],不细数了。
从上面的结果我们就会发现,造成吉布斯佯谬的原因并非来自全同粒子的能否分辨性。
其实,佯谬本质上是由粒子数密度的突变所引起的。在前面所讨论的例子中,当两种不同的气体混合后,粒子数密度由混合前的N/V变为N/2V,这正是造成等温混合时熵和内能发生变化的根本原因。如果容器隔板两边的气体完全相同,则抽取隔板前和抽取隔板后,粒子数密度没有发生变化,仍为N/V。所以,在等温混合后熵和内能没有发生变化。如果将每种气体在混合前后的粒子数密度分别用ρ和ρ′表示,那么在上面这个例子中,不同气体混合时混合前ρ=N/V、混合后ρ′=N/2V,相同气体混合时,混合前后ρ=ρ′=N/V。
为求等温混合前后熵的变化,可以将混合前后的熵分别写为
由此可得熵的变化为
(31)
对于不同气体ρ′/ρ=1/2,ρ′-ρ=-N/2V。将它们代入上式即可得到式(22),对于相同气体ρ′/ρ=1,ρ′-ρ=0,代入式(31)可得ΔS=0,熵没有变化,就不会出现上面的佯谬了,由此简并理想气体熵佯谬得以解决。
对于弱简并气体混合所产生的内能佯谬,将ρ=N/V与ρ′=N/2V代入,将混合前后内能分别改写为
等温混合后内能的变化为
(34)
对于不同气体,ρ′-ρ=-N/2V代入可得式(27),对于相同气体,ρ′-ρ=0代入式(34)得
ΔU=0
(35)
由此,弱简并理想气体的内能佯谬得以解决。
3 讨论与结论
综上所述,吉布斯佯谬源于热力学,产生吉布斯佯谬的原因在于计算的过程中忽略了粒子数密度的突变。
在混合气体中,无论两种气体性质多么接近,只要存在区别,在原则上都可以把它们区分开来,因而在气体混合后可以得到两种气体分子数密度减小为原来的二分之一,而且此过程是一个不可逆的绝热扩散过程,熵增大。
如果两种气体本来就是一种气体的两部分,在混合之后粒子数密度没有发生任何变化,虽然此过程两部分间的粒子仍然有“扩散”,对于经典单原子分子理想气体,它是量子理想气体满足非简并条件时的情景,同种组元的粒子仍然被认为是“全同的”,因此这种“扩散”是可逆的绝热过程,熵不变;对于量子气体,量子理论本身就要求同种组元的粒子是“全同的”,不认为此过程系统状态发生了变化,状态没变,熵当然不变。所以说ΔS,ΔU的突变来源于不同气体或同一种气体在混合过程中有无粒子数密度的突变。
我们认为:上述教材[3]由统计物理方法在考虑了“粒子全同性”对吉布斯佯谬的解释(实际也是持此观点一般教材中的解释)是不合适的。原因如下:第一,式(8)的熵是不正确的表达式,它实际是近独立的定域粒子系统熵的表达式,而不是非定域的麦克斯韦-玻耳兹曼(单原子分子经典理想气体)熵的表达式;第二,考虑了“粒子全同性”后的式(9)熵的表达式,如果不使用粒子数是否突变的方式,仍然得到的是类似于本文中式(22)的结果,而不是式(31)(尽管两式实际是相同的),也会出现类似于式(24)的结果,即吉布斯佯谬。换句话说:教材[3]解释的吉布斯佯谬的消除,也是利用的“粒子数密度”有无突变,而不是“粒子全同性”。
无论是热力学还是统计物理中,引起佯谬的根源是计算两种不同气体混合和同种气体混合时,注意粒子数密度是否突变是至关紧要的,如果考虑到这一因素佯谬就消除了。在传统的热力学教科书中,理想气体的熵写成温度和体积的函数S=S(T,V)或S=S(T,p),所以在处理气体等温混合时不能反映各组元粒子数密度的变化而只能反映参与混合的各部分气体体积(压强)的变化,因此将同种气体的混合当成异种气体混合来处理,从而得出同种气体等温混合过程中出现熵佯谬、内能佯谬和压强等佯谬。如果我们将S,U等表示为T和粒子数密度N/V的函数,佯谬就得到完整的解释。

